El artículo fue elaborado en vísperas del inicio del curso "Algoritmos y estructuras de datos"

El algoritmo de Johnson encuentra la ruta más corta entre todos los pares de vértices en un gráfico dirigido ponderado con pesos negativos sin contornos negativos.
¡Oh, cómo suena! Analicemos el enunciado del problema en partes.
, , ( – ), . , 4 8 :
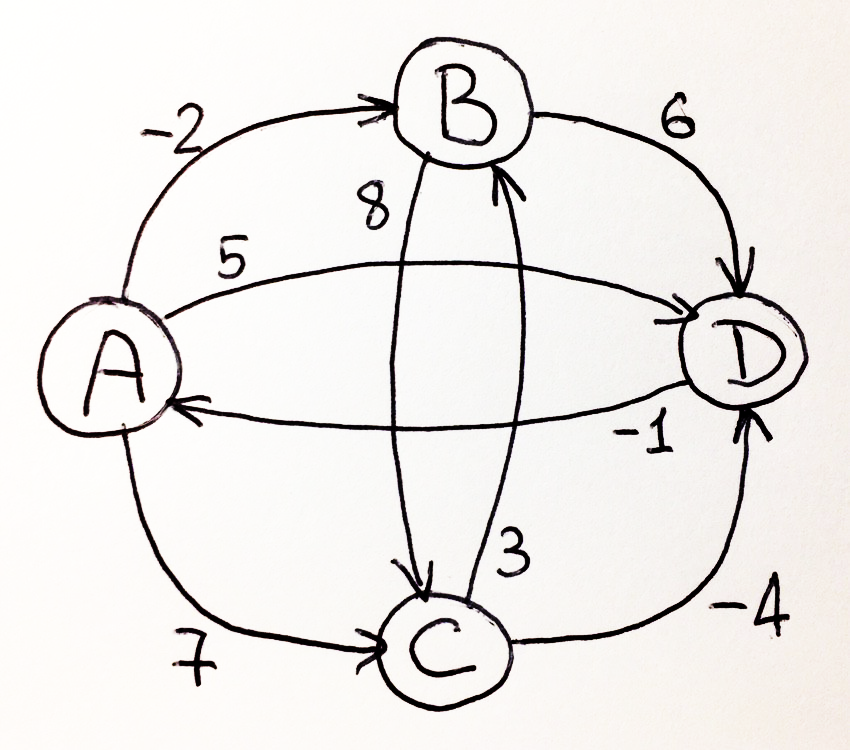
. «» «».
, «» «» . , . – . , D , .
, , , . . . «» «», , , .
, , , :
.
-, « » :
for k = 1 to n // n –
for x = 1 to n
for y = 1 to n
W[x][y] = min(W[x][y], W[x][k] + W[k][y]) W[x][y] .
W – . , .
«» . X Y , – .
- , – , – .
. , , , -.
, .

, , (-2), «» D (-2+6=4). . CD .
. , .
?
: ! : , , . !
?
– , . ? , .
, 4, A D : 5 + 1 * 4 = 9. 3 (A-B-C-D) 12 : -2 + 8 – 4 + 3 * 4 = 14.
, – , . ? XY h(X) h(Y), h(v) – «» , .
:
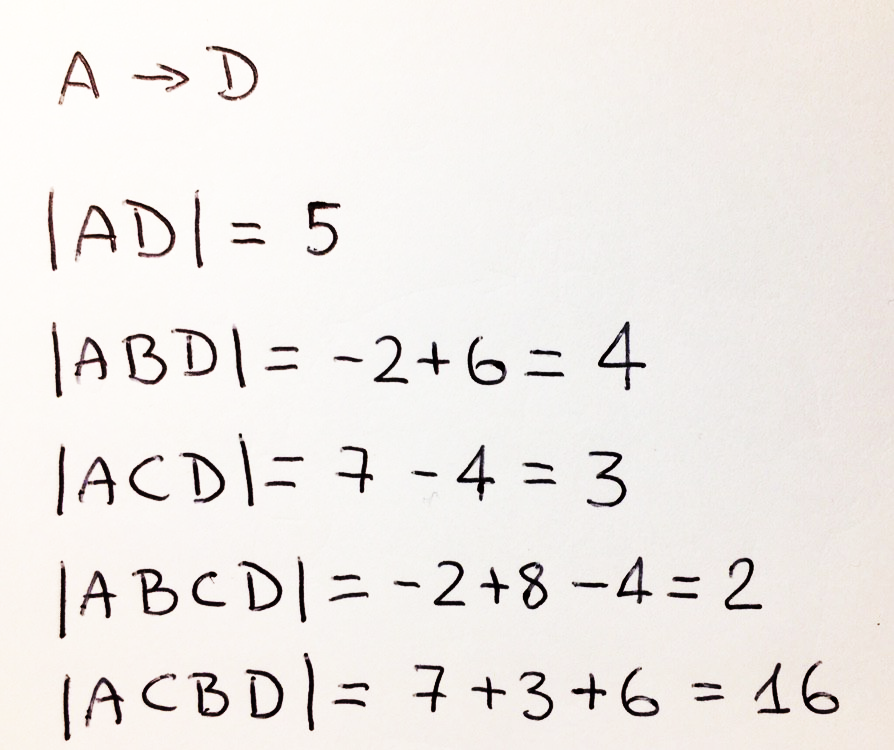 |
 |
 |
|---|
, A D:

, A D , h(A) – h(D), , , ! , .
h, .
,
- S, . , S S* , S, «» .
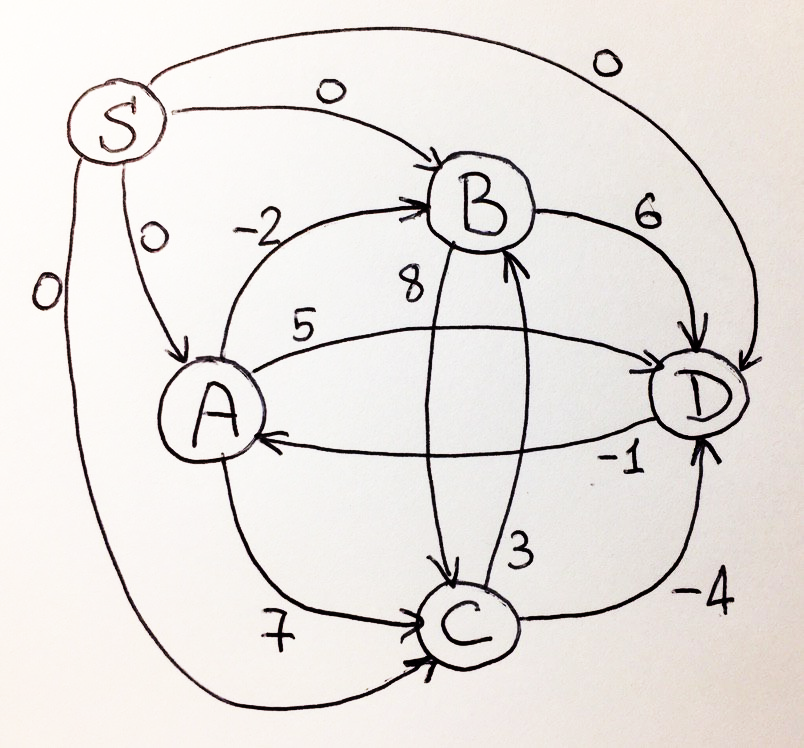
-, S . N «» S . «» , , :
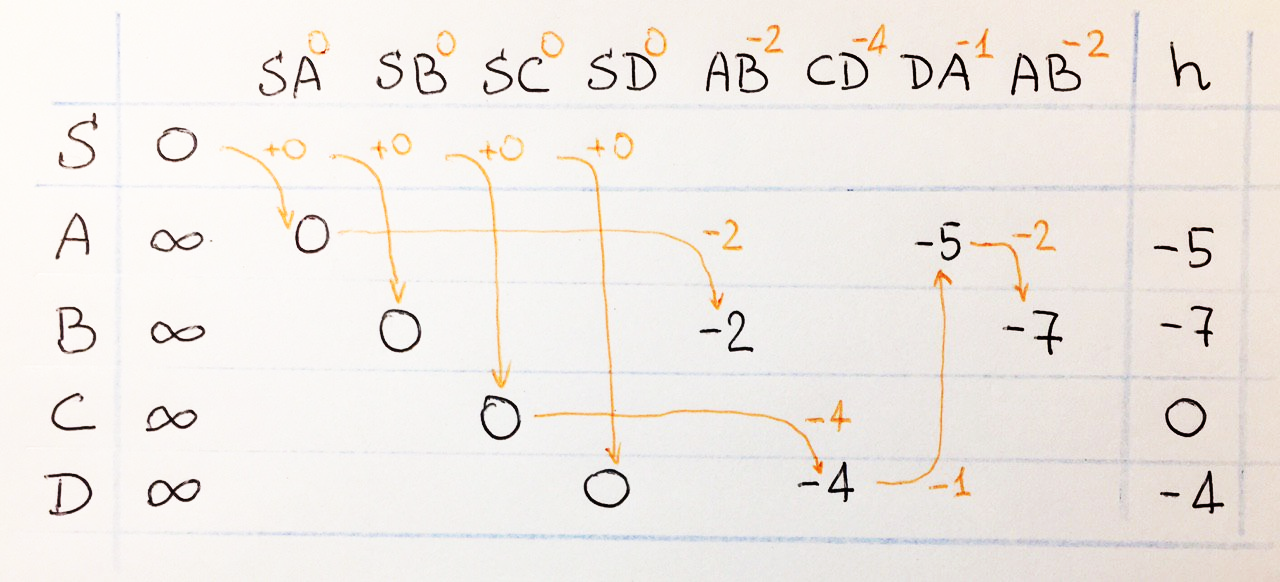
h . – S. S , h – . , , , , , , :
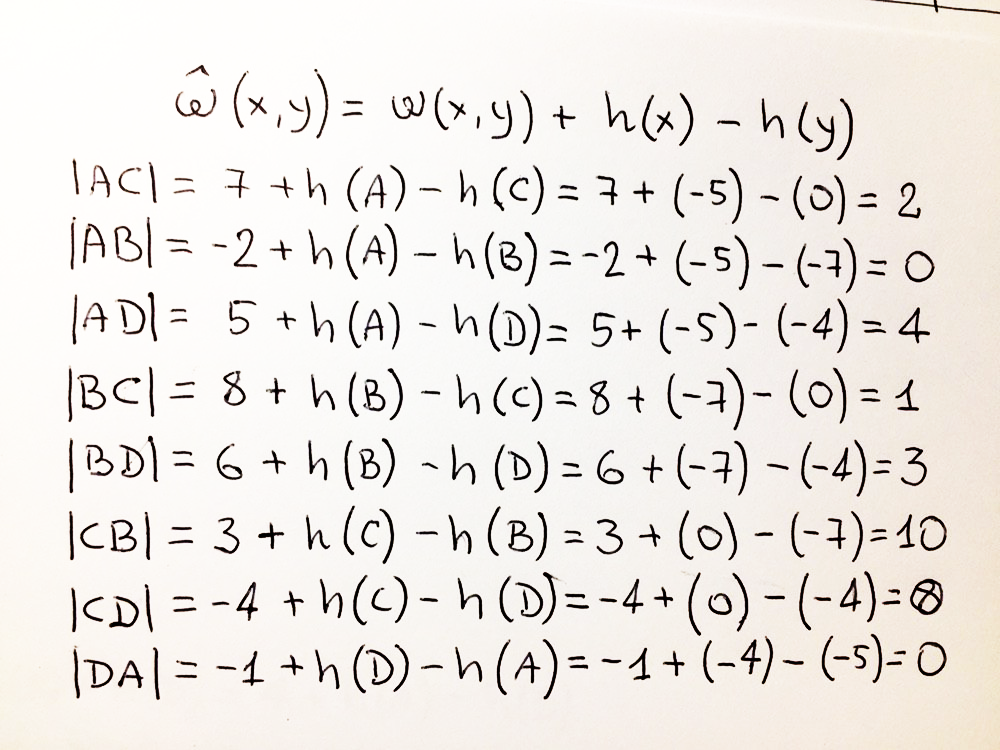
:
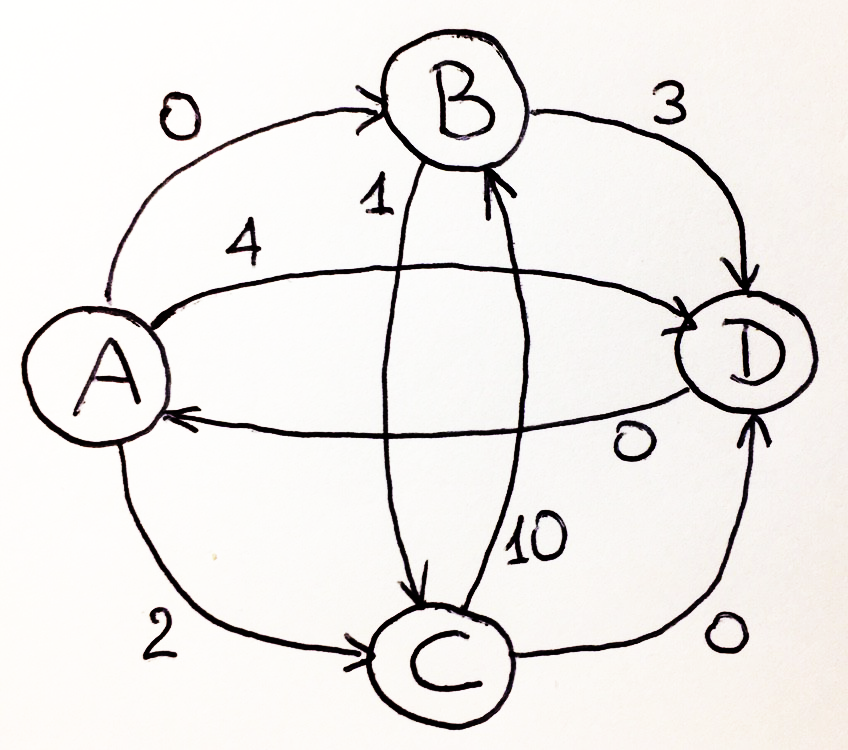
, , , ! .
, :
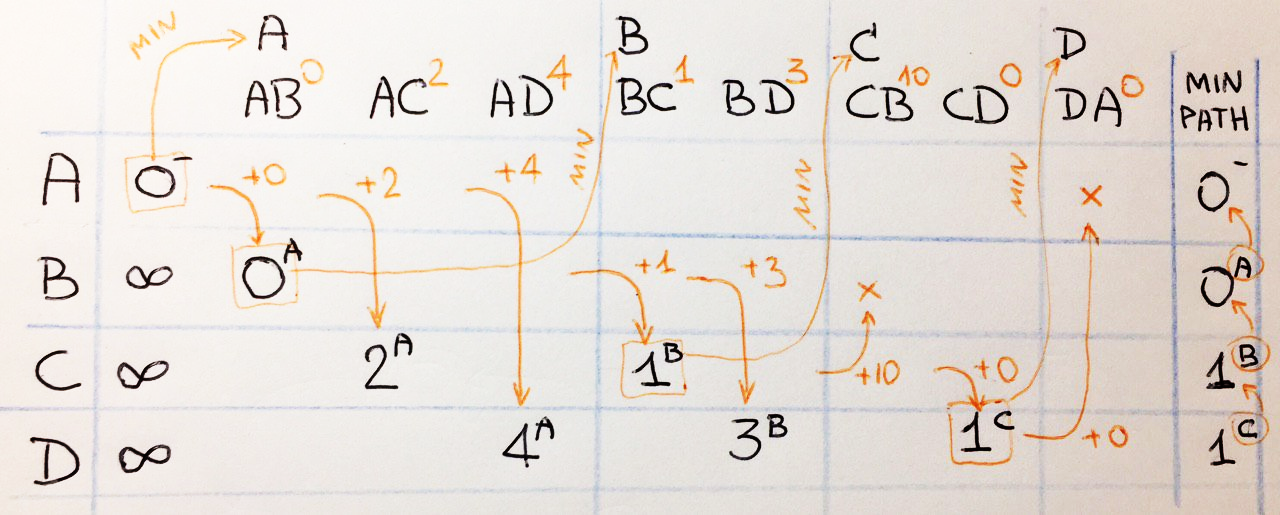
, , , . . , A D : A <= B <= C <= D, .
, . , .