¡Hola colegas! No he escrito sobre Habr durante cien años, pero ahora ha llegado el momento. Esta primavera, impartí el curso Advanced ML en MADE Big Data Academy de Mail.ru Group; Parece que a los oyentes les gustó, y ahora me pidieron que no escribiera tanto un post publicitario como un post educativo sobre uno de los temas de mi curso. La elección estuvo cerca de lo obvio: como ejemplo de un modelo probabilístico complejo, discutimos un modelo SIR epidemiológico extremadamente relevante (aparentemente ... pero más sobre eso más adelante) que modela la propagación de enfermedades en una población. Lo tiene todo: inferencia aproximada a través de métodos de Markov Monte Carlo y modelos ocultos de Markov con el algoritmo estocástico de Viterbi, e incluso datos de solo presencia.



Con este tema, solo surgió una pequeña dificultad: comencé a escribir sobre lo que realmente dije y mostré en la conferencia ... y de alguna manera, de manera rápida e imperceptible, acumulé veinte páginas de texto (bueno, con imágenes y código), que aún no es estaba terminado y no era autónomo en absoluto. Y si cuenta todo de tal manera que sea comprensible desde "cero" (no desde el cero absoluto, por supuesto), entonces podría escribir cien páginas. Así que algún día definitivamente los escribiré, pero por ahora les presento la primera parte de la descripción del modelo SIR, en la cual solo podemos plantear un problema y describir el modelo desde su lado generador - y si el público respetado tiene interés, entonces será posible Continuar.

Modelo SIR: declaración del problema

Amo a mis amigos y ellos me aman,

somos lo más cercanos que podemos ser.

Y solo porque realmente nos importa, ¡

lo que sea que obtengamos, lo compartimos!



Tom Lehrer. Lo conseguí de agnes

Así que averigüémoslo. De manera informal, los supuestos básicos del modelo SIR son los siguientes:

• hay una cierta población de personas en la que puede caminar algún virus terrible;
• inicialmente, el virus ingresa a la población de una forma u otra (por ejemplo, aparece la primera persona enferma), y luego las personas se infectan entre sí;
• SIR , :
  
     ○ Susceptible ( , , .. ),
  
     ○ Infected ( )
  
     ○ Recovered ().

Para simplificar, asumiremos que aquellos que han estado enfermos siempre desarrollan inmunidad y están excluidos del ciclo del virus en la naturaleza. En consecuencia, las transiciones entre estos estados solo pueden ser de izquierda a derecha: Susceptible → Infectado → Recuperado.



La tarea es, de hecho, entrenar este modelo, es decir, comprender algo sobre los parámetros del proceso de infección a partir de los datos. Es fácil entender cómo se ven los datos: es simplemente el número de infectados registrados en cada momento, que denotaremos por$$$\boldsymbol{y}$... Por ejemplo, cuando di mi tarea en el curso sobre coronavirus (se trataba, sin embargo, de otros modelos), los datos de Rusia se veían así:

[2,2,2,2,3,4,6,8,10,10,10,10,15,20,25,30,45,59,63,93,114,147,199,253,306,438,438,495,658,840,1036,1264,1534,1836,2337,2777,3548,4149,4731,5389,6343,7497,8672]

Pero cuáles son los parámetros de este modelo, cómo interactúan entre sí y cómo entrenarlos, especialmente en un conjunto de datos tan pequeño, es una pregunta más seria.



En general, seguiré el esquema general del trabajo ( Fintzi et al., 2016 ), que construye algoritmos MCMC para SIR, SEIR y algunas de sus variantes. Pero en comparación con ( Fintzi et al., 2016 ), simplificaré enormemente tanto el modelo como su presentación. La principal simplificación es que en lugar del tiempo continuo, que se considera en el trabajo original, consideraremos el tiempo discreto, es decir, en lugar de un proceso continuo que en algún momento genera eventos de la forma "infectado" y "recuperado", consideraremos que la gente pasa por un conjunto de puntos discretos en el tiempo$$$t=1,\ldots,T$... Esta simplificación nos permitirá, en primer lugar, deshacernos de muchas dificultades técnicas, y en segundo lugar, pasar del algoritmo Metropolis-Hastings en general al algoritmo de muestreo de Gibbs, es decir, no calcular el ratio de Metropolis, como es necesario hacer en ( Fintzi et al., 2016 ). Si no entiendes lo que acabo de decir, no te preocupes: no necesitaremos esto hoy, y si hay próximas partes, te lo explicaré todo.



Denotaremos los estados del modelo SIR por S, I y R, respectivamente, y el estado de una persona$$$i$ En el momento $$$t$ - a través de $$$x_i^{(t)}\in\{S, I, R\}$... Al mismo tiempo, introduciremos inmediatamente variables para el número total de pacientes que aún no se han enfermado.$$$S^{(t)}$enfermo $$$I^{(t)}$ y recuperado $$$R^{(t)}$ En el momento $$$t$... Hombre total tendremos$$$N$así que para cualquiera $$$t$ será ejecutado $$$S^{(t)} + I^{(t)} + R^{(t)} = N$... Y, como escribí anteriormente,$$$y^{(t)}$de ellos son personas enfermas registradas (probadas).



Los parámetros desconocidos del modelo son$$$\boldsymbol\theta = \{\beta, \mu, \rho, \boldsymbol{\pi}\}$dónde:

• $$$\boldsymbol\pi$ - la distribución inicial de casos; en otras palabras,$$$x^{(1)}_j\sim \boldsymbol{\pi}$ para cada $$$j$; en nuestro modelo simplificado, no entrenaremos$$$\boldsymbol\pi$, pero simplemente registraremos 1-2 casos en el primer momento;
• $$$\rho$ - la probabilidad de encontrar a una persona infectada en la población general, es decir, la probabilidad de que una persona $$$x_j$ en el momento $$$t$cuando $$$x_j^{(t)}=I$, se detectará mediante la prueba y se inscribirá en los datos $$$y^{(t)}$; en otras palabras, para cada persona enferma, lanzamos una moneda para determinar si la prueba la encontrará o no, por lo que el elemento actual es$$$y_t$ tiene una distribución binomial con parámetros $$$I^{(t)}$ y $$$\rho$:

  $$

  $$y^{(t)}\mid I^{(t)}, \rho \sim \mathrm{Binomial}(I^{(t)}, \rho);$$

• $$$\mu$ - la probabilidad de que la persona enferma se recupere en un paso de tiempo, es decir, la probabilidad de transición del estado $$$I$ en estado $$$R$;

Y $$$\beta$ - Este es el parámetro más interesante que muestra la probabilidad de infección en un recuento de tiempo de una persona infectada . Esto significa que en el modelo asumimos que todas las personas de la población se "comunican" entre sí ("comunicación" aquí significa contacto suficiente para la transmisión de la enfermedad; el coronavirus se transmite principalmente por gotitas en el aire, pero, por supuesto, es posible modelar y la propagación de cualquier otra enfermedad; ver, por ejemplo, el epígrafe), y la probabilidad de infectarse depende de cuántos están ahora infectados, es decir, de qué$$$I^{(t)}$... Asumiremos el modelo más simple, en el que la probabilidad de infección de una persona infectada es$$$\beta$, y todos estos eventos son independientes, lo que significa que la probabilidad de mantenerse saludable es

$$

$$(1-\beta)^{I^{(t)}}.$$

Estas suposiciones en realidad tienen mucho que discutir. Lo más sorprendente aquí, en mi opinión personal, es la distribución binomial para$$$y^{(t)}$... Lanzar una moneda con probabilidad de detectar a una persona infectada es absolutamente normal, pero no es muy realista que volvamos a lanzar esta moneda a cada paso, es decir, podemos “olvidarnos” de una persona infectada ya detectada. Como resultado, el modelo SIR puede (y a menudo lo hace) producir una secuencia completamente no monótona$$$\boldsymbol{y}$; esto es extraño, pero no parece tener un gran impacto en el resultado, y sería mucho más difícil modelar este proceso de manera más realista.



Además, es obvio que este modelo está destinado a una población cerrada, donde todos "se comunican" con todos, por lo que no tiene sentido lanzarlo, digamos, para Rusia con el parámetro N de cien millones o para Moscú con el parámetro diez millones (y computacionalmente no funcionará). Un área importante de extensiones y extensiones de los modelos SIR se dedica a esto: cómo agregar un gráfico más realista de interacciones y posibles infecciones; Probablemente hablemos de esto en el último post.



Pero con todas estas simplificaciones, ahora, usando los parámetros anteriores, podemos escribir la matriz de probabilidad de la transición entre estados. Estas probabilidades (más precisamente, específicamente la probabilidad de estar infectado) dependen de las estadísticas generales de la población. Designemos el vector de estados de todas las personas excepto$$$x_j$, a través de $$$\boldsymbol{x}_{-j}$y extender la misma notación a todas las demás variables; p.ej,$$$I_{-j}^{(t)}$ Es la cantidad de infectados a la vez $$$t$, por no mencionar $$$x_j$... Entonces, para las probabilidades de transición de$$$x_j^{(t-1)}$ a $$$x_j^{(t)}$ obtenemos

$$

$$p\left(x_j^{(t)}=S\mid x_j^{(t-1)}=S, \boldsymbol{x}_{-j}^{(t-1)}\right) = (1 - \beta)^{I_{-j}^{(t-1)}},$$

$$

$$p\left(x_j^{(t)}=I\mid x_j^{(t-1)}=S, \boldsymbol{x}_{-j}^{(t-1)}\right) = 1 - (1 - \beta)^{I_{-j}^{(t-1)}},$$

$$

$$p\left(x_j^{(t)}=R\mid x_j^{(t-1)}=I, \boldsymbol{x}_{-j}^{(t-1)}\right) = \mu,$$

$$

$$p\left(x_j^{(t)}=I\mid x_j^{(t-1)}=I, \boldsymbol{x}_{-j}^{(t-1)}\right) = 1 - \mu,$$

y en todos los demás casos

$$

$$p\left(x_j^{(t)}\mid x_j^{(t-1)}, \boldsymbol{x}_{-j}^{(t-1)}\right) = 0.$$

Lo mismo se puede escribir más claramente en forma de matriz de probabilidad de transición (el orden de filas y columnas es natural, SIR):

$$

$$\left(\begin{matrix} (1 - \beta)^{I_{-j}^{(t-1)}} & 1 - (1 - \beta)^{I_{-j}^{(t-1)}} & 0 \\ 0 & 1 - \mu & \mu \\ 0 & 0 & 1\end{matrix}\right)$$

Para un lector familiarizado con las cadenas de Markov y los modelos de Markov, puede parecer que este es solo un modelo de Markov oculto: hay un estado oculto, hay una distribución clara de los observables para cada estado oculto, las transiciones son realmente de Markov, es decir, el siguiente estado oculto depende solo del anterior ... Pero hay , como dicen, hay una salvedad: las probabilidades de transición no pueden considerarse constantes, cambian con el cambio$$$I^{(t)}$y este es un aspecto extremadamente esencial del modelo que no se puede desechar.



Por lo tanto, la inferencia en este modelo de repente se vuelve mucho más difícil que en el modelo de Markov oculto habitual (aunque tampoco siempre hay tal regalo allí). Sin embargo, aunque la conclusión es más complicada, todavía está sujeta a la mente humana; en las próximas instalaciones (si las hay) les contaré sobre esto. Y por hoy, casi es suficiente, ahora relajémonos un poco e intentemos jugar con este modelo por ahora en un sentido generativo.

Ejemplo de generación de datos

Como gran conocedor y experto, un

introvertido entró en cuarentena.

***

“No podía trabajar en casa”,

trató de explicar la abeja a los gusanos.

***

Kaganov murió bromeando alegremente.

Por supuesto, lo siento mucho por él ...



Leonid Kaganov. Cuarentenas

Si se conocen los parámetros del modelo, y solo se necesita generar una trayectoria de cómo se desarrollaría la propagación de la enfermedad en la población, no hay nada complicado en SIR. El siguiente código genera un ejemplo de una población según nuestro modelo; afirma que codifiqué como$$$S=0$, $$$I=1$, $$$R=2$... Como advertí, por simplicidad asumiré que en este momento$$$t=0$ hay exactamente una persona enferma en la población, y luego continúa.

def sample_population(N, T, true_rho, true_beta, true_mu):
    true_log1mbeta = np.log(1 - true_beta)

    cur_states = np.zeros(N)
    cur_states[:1] = 1
    cur_I, test_y, true_statistics = 1, [1], [[N-1, 1, 0]]

    for t in range(T):
        logprob_stay_healthy = cur_I * true_log1mbeta
        for i in range(N):
            if cur_states[i] == 0 and np.random.rand() < -np.expm1(logprob_stay_healthy):
                cur_states[i] = 1
            elif cur_states[i] == 1 and np.random.rand() < true_mu:
                cur_states[i] = 2

        cur_I = np.sum(cur_states == 1)
        test_y.append( np.random.binomial( cur_I, true_rho ) )
        true_statistics.append([np.sum(cur_states == 0), np.sum(cur_states == 1), np.sum(cur_states == 2)])

    return test_y, np.array(true_statistics).T

N, T, true_rho, true_beta, true_mu = 100, 20, 0.1, 0.05, 0.1
test_y, true_statistics = sample_population(N, T, true_rho, true_beta, true_mu)

Este código proporciona no solo los datos reales $$$\boldsymbol{y}$sino también estadísticas "verdaderas" $$$S^{(t)}$, $$$I^{(t)}$, $$$R^{(t)}$para que se puedan visualizar. Vamos a hacerlo; para los parámetros$$$N=100$, $$$T=20$, $$$\rho=0.1$, $$$\beta=0.2$, $$$\mu=0.3$puede obtener algo como esto:







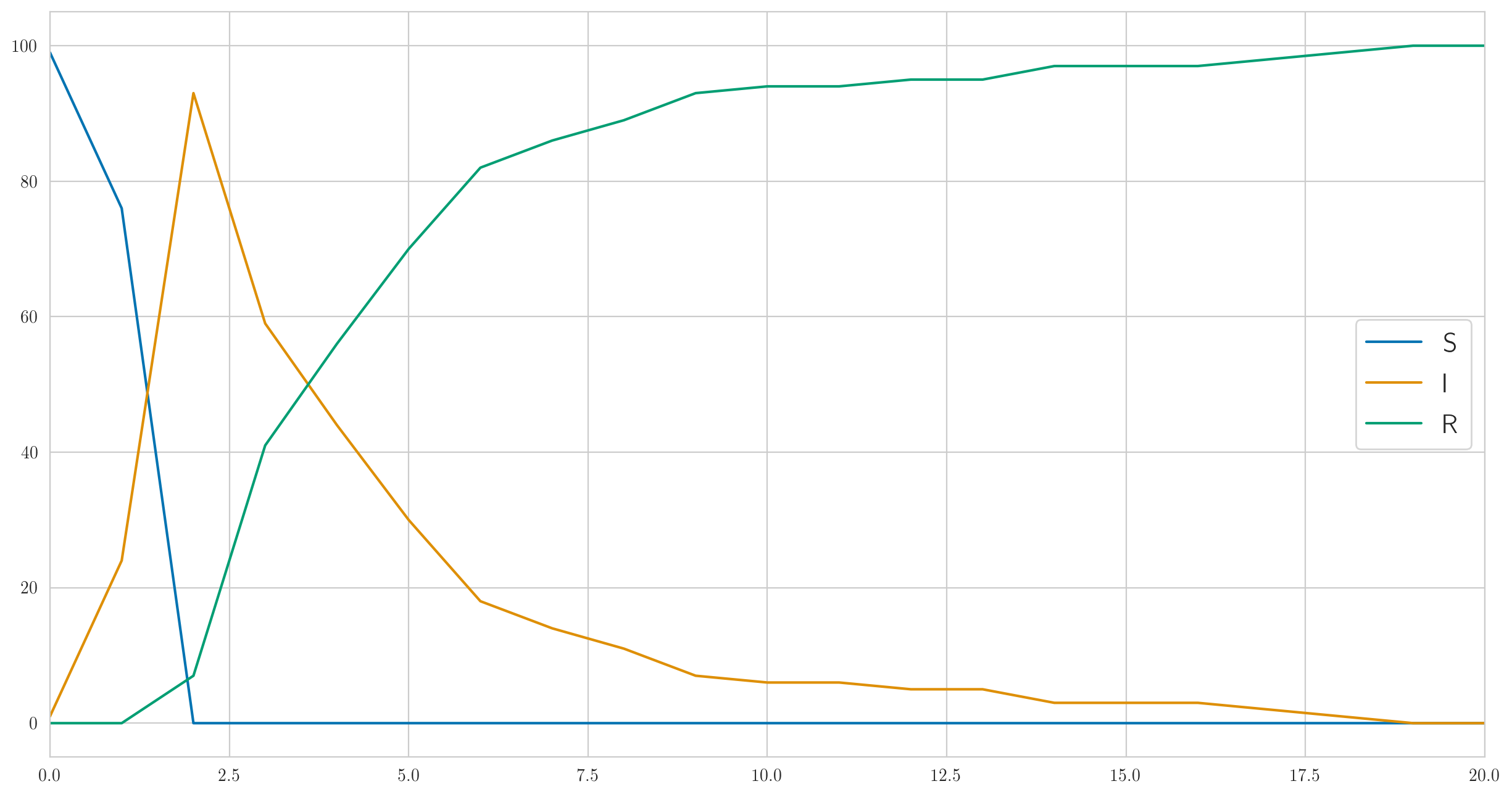
como puede ver, en este ejemplo todos se enferman muy rápidamente y luego, lentamente, comienzan a mejorar. Y los datos reales observados sobre los enfermos se ven así:

[1 6 13 6 6 4 1 0 0 1 0 1 2 0 0 0 0 0 1 0 0]

Tenga en cuenta que, como discutimos anteriormente, aquí no hay monotonía.



Pero este no es ciertamente el único comportamiento posible. Elegí los parámetros anteriores para que la infección fuera lo suficientemente rápida y la enfermedad cubriera casi de inmediato a las cien personas de nuestra población de prueba. Y si lo haces$$$\beta$ más pequeño, por ejemplo $$$\beta=0.01$, entonces la infección irá mucho más lentamente, y ni siquiera todos tendrán tiempo de enfermarse antes de que la última persona enferma se recupere y no se quede. Algo como esto:







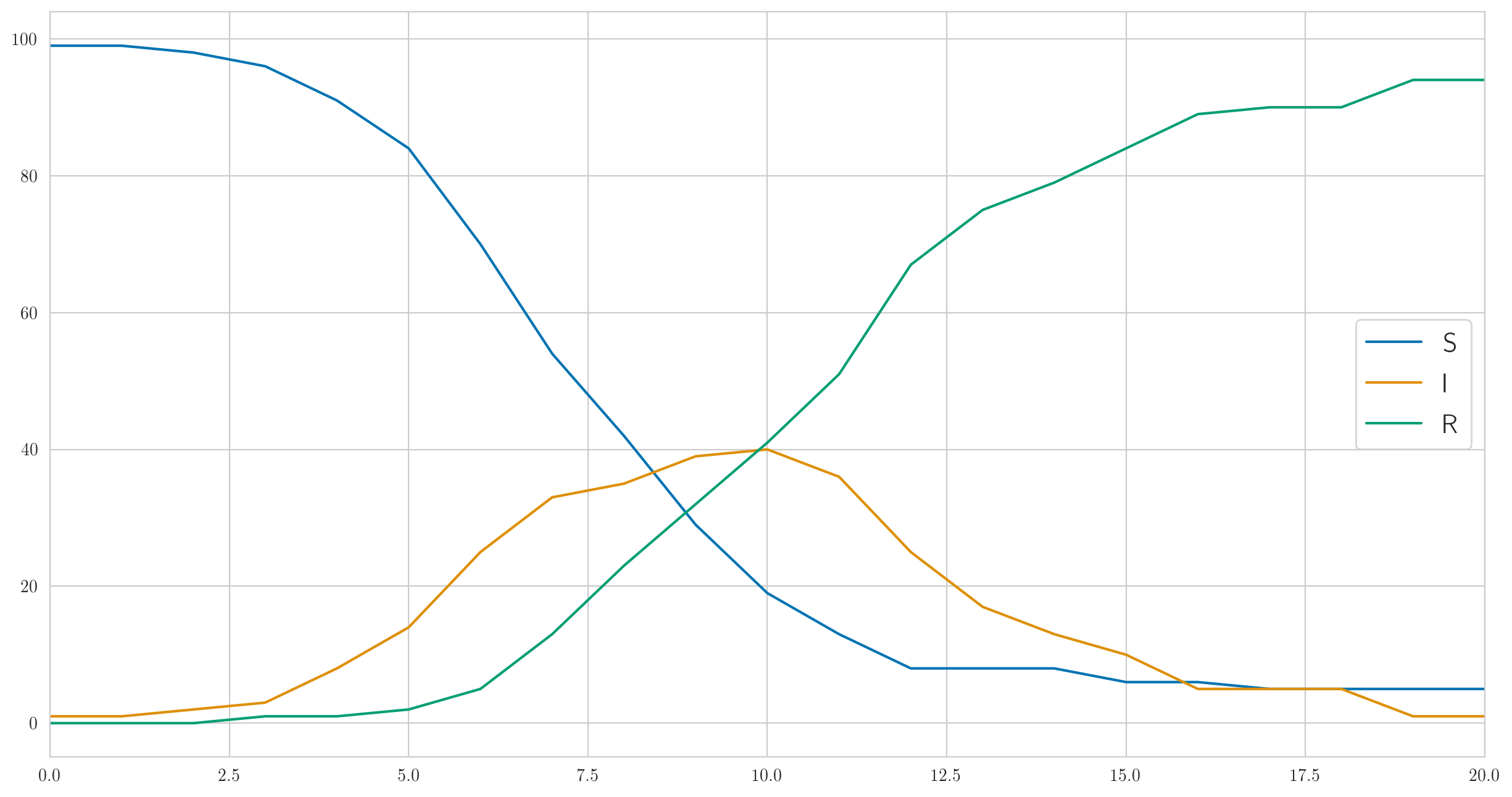
Y el número de casos detectados también es completamente diferente:

[1 0 0 0 0 1 2 2 3 1 1 9 3 1 3 1 0 1 0 0 0]

Es posible "estrangular" la enfermedad aún más; por ejemplo, vamos$$$\beta=0.01$pero pon $$$\mu=0.5$, es decir, en cada intervalo de tiempo, cada enfermo tiene una posibilidad de recuperarse en 0,5 (al final, esto es lógico: o se recuperará o no). Entonces, solo 50-60 de cada 100 personas se enfermarán con el terrible virus; las curvas pueden verse así:

[1 0 0 1 3 2 1 1 0 3 0 0 0 0 0 1 0 0 0 0 0]

Pero el panorama general, por supuesto, en cualquier caso parece el mismo: primero crecimiento exponencial y luego la salida a la saturación; la única diferencia es si el último operador tiene tiempo de recuperarse antes de reiniciar todos.



Bueno, es hora de resumir los resultados provisionales. Hoy hemos visto cómo es uno de los modelos epidemiológicos más simples. A pesar de muchas suposiciones que simplifican demasiado, el modelo SIR sigue siendo muy útil incluso en esta forma; el hecho es que la mayoría de sus extensiones son bastante sencillas y no cambian la esencia general del asunto. Por tanto, si continuamos, en la próxima serie hablaré de cómo entrenar un modelo SIR; sin embargo, esto implicará tantas cosas interesantes que probablemente tampoco quepa en una publicación. ¡Hasta la proxima vez!