El aprendizaje automático (ML) ya está cambiando el mundo. Google usa IO para ofrecer y mostrar respuestas a las búsquedas de los usuarios. Netflix lo usa para recomendar películas para la noche. Y Facebook lo usa para sugerir nuevos amigos que quizás conozcas.
El aprendizaje automático nunca ha sido más importante y, al mismo tiempo, tan difícil de aprender. Esta área está llena de jerga, y la cantidad de algoritmos de ML diferentes crece cada año.
Este artículo le presentará los conceptos fundamentales en el aprendizaje automático. Más específicamente, discutiremos los conceptos básicos de los 9 algoritmos de ML más importantes en la actualidad.
Sistema de recomendación
Para construir un sistema de recomendación completo desde 0 se requiere un conocimiento profundo de álgebra lineal. Debido a esto, si nunca ha estudiado esta disciplina, puede ser difícil comprender algunos de los conceptos de esta sección.
Pero no se preocupe: la biblioteca de Python scikit-learn hace que sea bastante fácil construir un CP. Por lo tanto, no necesita ese conocimiento profundo de álgebra lineal para construir un CP funcional.
¿Cómo funciona el CP?
Hay 2 tipos principales de sistemas de recomendación:
- Basado en contenido
- Filtración colaborativa
Un sistema basado en contenido hace recomendaciones basadas en la similitud de elementos que ya ha utilizado. Estos sistemas se comportan exactamente como espera que se comporte el CP.
El filtrado de colaboración CP proporciona recomendaciones basadas en el conocimiento de cómo el usuario interactúa con los elementos (* nota: las interacciones con elementos de otros usuarios que tienen un comportamiento similar al del usuario se toman como base). En otras palabras, usan la "sabiduría de la multitud" (de ahí la "colaboración" en el nombre del método).
En el mundo real, el filtrado colaborativo de CP es mucho más común que un sistema basado en contenido. Esto se debe principalmente al hecho de que generalmente dan mejores resultados. Algunos expertos también encuentran que el sistema colaborativo es más fácil de entender.
El filtrado colaborativo CP también tiene una característica única que no se encuentra en un sistema basado en contenido. A saber, tienen la capacidad de aprender características por su cuenta.
Esto significa que incluso pueden comenzar a definir similitudes en elementos basados en propiedades o rasgos que ni siquiera proporcionó para que este sistema funcione.
Hay 2 subcategorías de filtrado colaborativo:
- Basado en el modelo
- Basado en el vecindario
La buena noticia es que no necesita saber la diferencia entre estos dos tipos de filtrado colaborativo de CP para tener éxito en ML. Es suficiente saber que hay varios tipos.
Resumir
Aquí hay un resumen rápido de lo que hemos aprendido sobre el sistema de recomendaciones en este artículo:
- Ejemplos de sistemas de recomendación del mundo real
- Diferentes tipos de sistema de recomendación y por qué el filtrado colaborativo se usa con más frecuencia que el sistema basado en contenido
- La relación entre el sistema de recomendación y el álgebra lineal.
Regresión lineal
La regresión lineal se usa para predecir algún valor de y basado en un conjunto de valores de x.
Historia de regresión lineal.
La regresión lineal (LR) fue inventada en 1800 por Francis Galton. Galton era un científico que estudiaba el vínculo entre padres e hijos. Más específicamente, Galton investigó la relación entre el crecimiento de los padres y el crecimiento de sus hijos. El primer descubrimiento de Galton fue el hecho de que el crecimiento de los hijos, como regla, era casi lo mismo que el crecimiento de sus padres. Lo cual no es sorprendente.
Más tarde, Galton descubrió algo más interesante. El crecimiento del hijo, como regla, estaba más cerca de la estatura promedio general de todas las personas que del crecimiento de su propio padre.
Galton llamó a este fenómeno regresión . Específicamente, dijo: "La altura del hijo tiende a retroceder (o desplazarse hacia) la altura promedio".
Esto condujo a un campo completo en estadística y aprendizaje automático llamado regresión.
Matemática de regresión lineal
En el proceso de crear un modelo de regresión, todo lo que intentamos hacer es dibujar una línea lo más cerca posible de cada punto del conjunto de datos.
Un ejemplo típico de este enfoque es el enfoque de regresión lineal de "mínimos cuadrados", que calcula la cercanía de una línea en la dirección de arriba a abajo.
Ejemplo de ilustración:
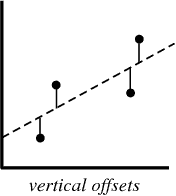
cuando crea un modelo de regresión, su producto final es una ecuación que puede usar para predecir los valores de y para el valor de x sin conocer de antemano el valor de y.
Regresión logística
La regresión logística es similar a la regresión lineal, excepto que en lugar de calcular el valor de y, evalúa a qué categoría pertenece un punto de datos dado.
¿Qué es la regresión logística?
La regresión logística es un modelo de aprendizaje automático utilizado para resolver problemas de clasificación.
A continuación se presentan algunos ejemplos de las tareas de clasificación de MO:
- Correo electrónico no deseado (¿correo no deseado o no?)
- Reclamación de seguro de automóvil (¿compensación o reparación?)
- Diagnóstico de enfermedades.
Cada una de estas tareas tiene claramente 2 categorías, lo que las convierte en ejemplos de tareas de clasificación binaria.
La regresión logística funciona bien para problemas de clasificación binaria: simplemente asignamos diferentes categorías a 0 y 1, respectivamente.
¿Por qué la regresión logística? Porque no puede usar la regresión lineal para las predicciones de clasificación binaria. Simplemente no funcionará, ya que intentará dibujar una línea recta a través de un conjunto de datos con dos valores posibles.
Esta imagen puede ayudarlo a comprender por qué la regresión lineal es mala para la clasificación binaria:
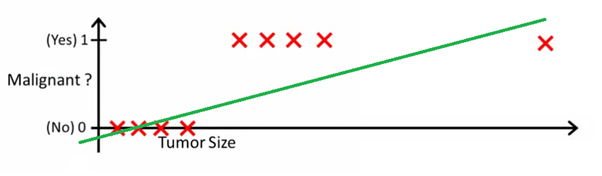
En esta imagen, el eje y representa la probabilidad de que el tumor sea maligno. Los valores 1-y representan la probabilidad de que el tumor sea benigno. Como puede ver, el modelo de regresión lineal funciona muy mal para predecir la probabilidad de la mayoría de las observaciones en el conjunto de datos.
Por eso es útil el modelo de regresión logística. Tiene una curva hacia la línea de mejor ajuste, lo que lo hace mucho más adecuado para predecir datos cualitativos (categóricos).
Aquí hay un ejemplo que compara modelos de regresión lineal y logística en los mismos datos:
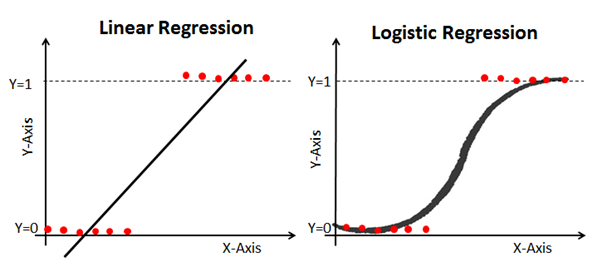
Sigmoide (la función sigmoidea)
La razón por la cual la regresión logística está retorcida es porque no utiliza una ecuación lineal para calcularla. En cambio, el modelo de regresión logística se construye usando un sigmoide (también llamado función logística porque se usa en regresión logística).
No tiene que memorizar el sigmoide a fondo para tener éxito en ML. Aún así, será útil tener una idea de esta característica.
Fórmula sigmoidea: La
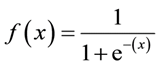
característica principal de un sigmoide, que vale la pena tratar, no importa qué valor pase a esta función, siempre devolverá un valor entre 0-1.
Usando un modelo de regresión logística para predicciones
Para utilizar la regresión logística para las predicciones, generalmente necesita definir con precisión el punto de corte. Este punto de corte suele ser 0,5.
Usemos nuestro ejemplo de diagnóstico de cáncer del gráfico anterior para ver este principio en la práctica. Si el modelo de regresión logística devuelve un valor inferior a 0,5, ese punto de datos se clasificará como benigno. Del mismo modo, si el sigmoide da un valor superior a 0,5, entonces el tumor se clasifica como maligno.
Usando una matriz de error para medir la efectividad de la regresión logística
La matriz de error puede usarse como una herramienta para comparar puntajes verdaderos positivos, verdaderos negativos, falsos positivos y falsos negativos en MO.
La matriz de error es particularmente útil cuando se usa para medir el rendimiento de un modelo de regresión logística. Aquí hay un ejemplo de cómo podemos utilizar la matriz de error:
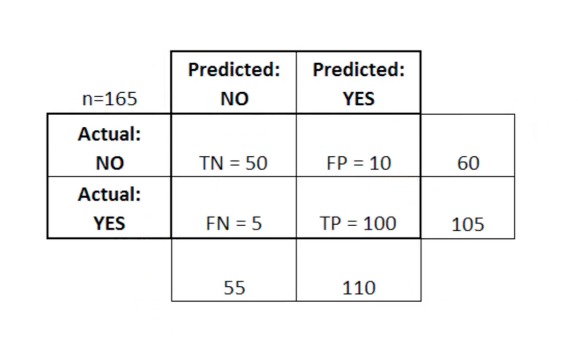
en esta tabla, TN significa verdadero negativo, FN significa falso negativo, FP significa falso positivo, TP significa verdadero positivo.
Una matriz de error es útil para evaluar un modelo si hay cuadrantes "débiles" en la matriz de error. Como ejemplo, puede tener un número anormalmente alto de falsos positivos.
También es bastante útil en algunos casos para garantizar que su modelo funcione correctamente en un área particularmente peligrosa de la matriz de errores.
En este ejemplo de diagnóstico de cáncer, por ejemplo, le gustaría asegurarse de que su modelo no tenga demasiados falsos positivos porque Esto significará que diagnosticó el tumor maligno de alguien como benigno.
Resumir
En esta sección, conoció por primera vez el modelo ML: regresión logística.
Aquí hay un resumen rápido de lo que ha aprendido sobre la regresión logística:
- Tipos de problemas de clasificación que son adecuados para resolver con regresión logística
- La función logística (sigmoide) siempre da un valor entre 0 y 1
- Cómo usar los puntos de corte para predecir con un modelo de regresión logística
- ¿Por qué es útil una matriz de error para medir el rendimiento de un modelo de regresión logística?
Algoritmo K-Vecinos más cercanos
El algoritmo k-vecinos más cercanos puede ayudar a resolver el problema de clasificación en el caso de que haya más de 2 categorías.
¿Cuál es el algoritmo k-vecinos más cercanos?
Este es un algoritmo de clasificación basado en un principio simple. De hecho, el principio es tan simple que es mejor demostrarlo con un ejemplo.
Imagine que tiene datos de altura y peso para futbolistas y jugadores de baloncesto. El algoritmo k-vecinos más cercanos se puede utilizar para predecir si un nuevo jugador es un jugador de fútbol o un jugador de baloncesto. Para hacer esto, el algoritmo determina los K puntos de datos más cercanos al objeto de estudio.
Esta imagen demuestra este principio con el parámetro K = 3:
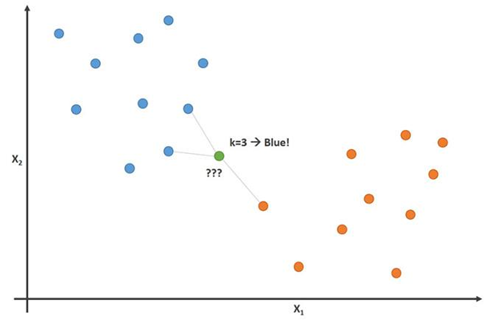
En esta imagen, los jugadores de fútbol son azules y los jugadores de baloncesto son naranjas. El punto que estamos tratando de clasificar es de color verde. Dado que la mayoría (2 de 3) las marcas más cercanas al punto verde son de color azul (jugadores de fútbol), el algoritmo K-vecinos más cercano predice que el nuevo jugador también será un jugador de fútbol.
Cómo construir un algoritmo K-vecinos más cercanos
Los principales pasos para construir este algoritmo:
- Recoge todos los datos
- Calcule la distancia euclidiana desde el nuevo punto de datos x a todos los demás puntos en el conjunto de datos
- Ordenar puntos del conjunto de datos en orden ascendente de distancia a x
- Predecir la respuesta usando la misma categoría que la mayoría de los datos K más cercanos a x
Importancia de la variable K en el algoritmo de vecinos K más cercanos
Si bien esto puede no ser obvio desde el principio, cambiar el valor K en este algoritmo cambiará la categoría en la que se encuentra el nuevo punto de datos.
Más específicamente, un valor K demasiado pequeño hará que su modelo prediga con precisión en el conjunto de datos de entrenamiento, pero será extremadamente ineficaz en los datos de la prueba. Además, tener una K demasiado alta hará que el modelo sea innecesariamente complejo.
La siguiente ilustración muestra este efecto perfectamente:
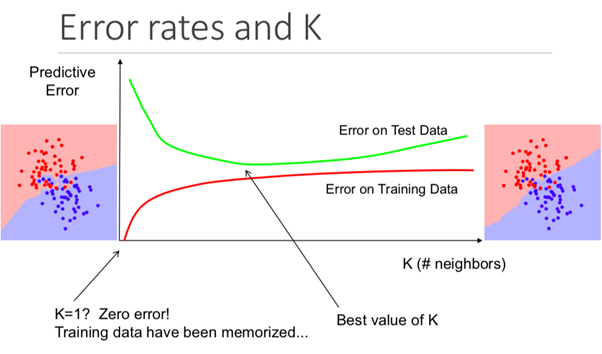
Pros y contras del algoritmo K-vecinos más cercanos
Para resumir nuestra introducción a este algoritmo, analicemos brevemente los pros y los contras de usarlo.
Pros:
- El algoritmo es simple y fácil de entender.
- Modelo de entrenamiento trivial sobre nuevos datos de entrenamiento
- Funciona con cualquier número de categorías en una tarea de clasificación.
- Agregue fácilmente más datos a muchos datos
- El modelo solo toma 2 parámetros: K y la métrica de distancia que le gustaría usar (generalmente distancia euclidiana)
Desventajas:
- Alto costo de cómputo, porque necesita procesar toda la cantidad de datos
- No funciona tan bien con parámetros categóricos
Resumir
Un resumen de lo que acaba de aprender sobre el algoritmo vecino K-Nearest:
- Un ejemplo de un problema de clasificación (jugadores de fútbol o baloncesto) que el algoritmo puede resolver
- Cómo utiliza el algoritmo la distancia euclidiana a los puntos vecinos para predecir a qué categoría pertenece un nuevo punto de datos
- Por qué los valores de K son importantes para pronosticar
- Pros y contras de usar el algoritmo K-vecinos más cercanos
Árboles de decisión y bosques al azar
El árbol de decisión y el bosque aleatorio son 2 ejemplos de un método de árbol. Más precisamente, los árboles de decisión son modelos ML utilizados para predecir recorriendo cada función en un conjunto de datos uno por uno. Un bosque aleatorio es un conjunto (comité) de árboles de decisión que usan órdenes aleatorias de objetos en un conjunto de datos.
¿Qué es un método de árbol?
Antes de sumergirnos en los fundamentos teóricos del método basado en árboles en ML, es útil comenzar con un ejemplo.
Imagina que juegas baloncesto todos los lunes. Además, siempre invitas al mismo amigo a jugar contigo. A veces viene un amigo, a veces no. La decisión de venir o no depende de muchos factores: qué tipo de clima, temperatura, viento y fatiga. Comienza a notar estas características y las rastrea junto con la decisión de su amigo de jugar o no.
Puede usar estos datos para predecir si su amigo vendrá hoy o no. Una técnica que puede usar es un árbol de decisión. Así es como se ve:
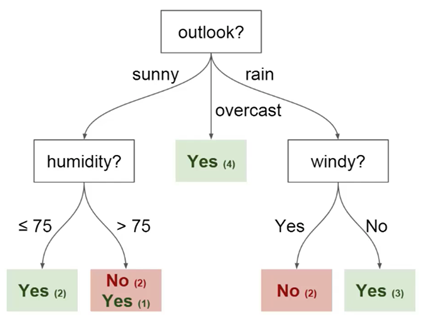
cada árbol de decisión tiene 2 tipos de elementos:
- Nodos: lugares donde se divide el árbol en función del valor de un determinado parámetro
- Bordes: el resultado de la división que conduce al siguiente nodo
Puede ver que el diagrama tiene nodos para la perspectiva, la humedad y el
viento. Y también las facetas para cada valor potencial de cada uno de estos parámetros.
Aquí hay un par de definiciones más que debe comprender antes de comenzar:
- Raíz - el nodo desde el cual comienza la división del árbol
- Hojas: los nodos finales que predicen el resultado final
Ahora tiene una comprensión básica de lo que es un árbol de decisión. En la siguiente sección, veremos cómo construir un árbol de este tipo desde cero.
Cómo construir un árbol de decisión desde cero
Construir un árbol de decisión es más complicado de lo que parece. Esto se debe a que decidir en qué ramificaciones (características) dividir sus datos (que es un tema del campo de la entropía y la adquisición de datos) es una tarea matemáticamente difícil.
Para resolver este problema, los especialistas en ML generalmente usan muchos árboles de decisión, aplicando conjuntos aleatorios de características elegidas para dividir el árbol en ellos. En otras palabras, se eligen nuevos conjuntos aleatorios de características para cada árbol separado, en cada partición separada. Esta técnica se llama bosques aleatorios.
En general, los expertos generalmente eligen el tamaño de un conjunto aleatorio de características (denotado por m) para que sea la raíz cuadrada del número total de características en el conjunto de datos (denotado por p). En resumen, m es la raíz cuadrada de p, y luego se selecciona aleatoriamente una característica específica de m.
Beneficios de usar un bosque aleatorio
Imagine que está trabajando con muchos datos que tienen una característica "fuerte". En otras palabras, hay una característica en este conjunto de datos que es mucho más predecible en términos del resultado final que otras características de este conjunto de datos.
Si está construyendo un árbol de decisión a mano, entonces tiene sentido usar esta característica para la partición "superior" de su árbol. Esto significa que tendrá varios árboles cuyas predicciones están altamente correlacionadas.
Queremos evitar esto porque El uso de la media de variables altamente correlacionadas no reduce significativamente la varianza. Mediante el uso de conjuntos aleatorios de características para cada árbol en un bosque aleatorio, decorrelacionamos los árboles y se reduce la varianza del modelo resultante. Esta decorrelación es una gran ventaja en el uso de bosques aleatorios sobre árboles de decisión construidos a mano.
Resumir
Aquí hay un resumen rápido de lo que acaba de aprender sobre los árboles de decisión y los bosques aleatorios:
- Un ejemplo de un problema cuya solución se puede predecir usando un árbol de decisión
- Elementos del árbol de decisión: nodos, caras, raíces y hojas.
- Cómo el uso de un conjunto aleatorio de características nos permite construir un bosque aleatorio
- ¿Por qué usar un bosque aleatorio para la descorrelación de variables puede ser útil para reducir la varianza del modelo resultante?
Máquinas de vectores de soporte
Las máquinas de vectores de soporte son un algoritmo de clasificación (aunque, técnicamente hablando, también se pueden usar para resolver problemas de regresión) que divide un conjunto de datos en categorías en las "brechas" más grandes entre categorías. Este concepto se vuelve más claro cuando observa el siguiente ejemplo.
¿Qué es la máquina de vectores de soporte?
Una máquina de vectores de soporte (SVM) es un modelo de ML supervisado con algoritmos de aprendizaje apropiados que analizan datos y reconocen patrones. El SVM puede usarse tanto para tareas de clasificación como para análisis de regresión. En este artículo, veremos específicamente el uso de máquinas de vectores de soporte para resolver problemas de clasificación.
¿Cómo funciona el MOU?
Profundicemos en cómo funciona realmente el MOU.
Se nos da un conjunto de ejemplos de capacitación, cada uno de los cuales está marcado como perteneciente a una de las 2 categorías, y al usar este conjunto de SVM, creamos un modelo. Este modelo clasifica los nuevos ejemplos en una de dos categorías. Esto hace que el SVM sea un clasificador lineal binario improbable.
El MOU usa geometría para hacer predicciones por categoría. Más específicamente, la máquina de vectores de soporte asigna puntos de datos como puntos en el espacio y los clasifica para que estén separados por el mayor espacio posible. La predicción de que los nuevos puntos de datos pertenecerán a una categoría particular se basa en qué lado del punto de ruptura se encuentra.
Aquí hay un ejemplo de visualización para ayudarlo a comprender la intuición del MOU:
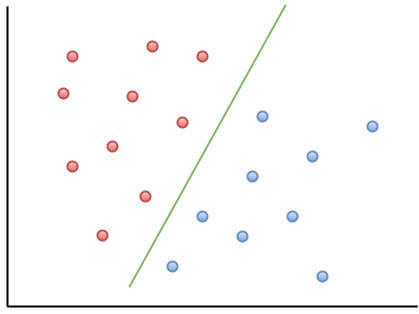
Como puede observar, si un nuevo punto de datos cae a la izquierda de la línea verde, se lo denominará "rojo", y si a la derecha, se lo denominará "azul". Esta línea verde se llama hiperplano y es un término importante para trabajar con MOU.
Echemos un vistazo a la siguiente representación visual de la SVM:
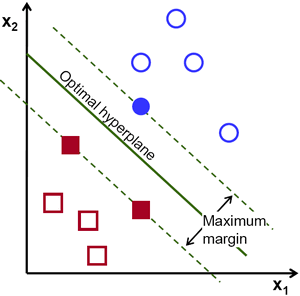
en este diagrama, el hiperplano se etiqueta como el "hiperplano óptimo". La teoría de la máquina de vectores de soporte define un hiperplano óptimo como un hiperplano que maximiza el campo entre los dos puntos de datos más cercanos de diferentes categorías.
Como puede ver, el límite del campo sí afecta a 3 puntos de datos: 2 de la categoría roja y 1 de la azul. Estos puntos, que están en contacto con el borde del campo, se denominan vectores de soporte, de ahí su nombre.
Resumir
Aquí hay una instantánea rápida de lo que acaba de aprender sobre las máquinas de vectores de soporte:
- El MOU es un ejemplo de un algoritmo de ML supervisado
- El vector de soporte se puede utilizar para resolver problemas de clasificación y análisis de regresión.
- Cómo el MOU clasifica los datos usando un hiperplano que maximiza el margen entre categorías en el conjunto de datos
- Los puntos de datos que tocan los límites del campo de división se denominan vectores de soporte. De aquí proviene el nombre del método.
Agrupamiento de medias K
El método K-Means es un algoritmo de aprendizaje automático no supervisado. Esto significa que acepta datos sin etiquetar e intenta agrupar grupos de observaciones similares en sus datos. El método K-Means es extremadamente útil para resolver aplicaciones del mundo real. Aquí hay ejemplos de varias tareas que se ajustan a este modelo:
- Segmentación de clientes para equipos de marketing.
- Clasificación de documentos.
- Optimización de rutas de envío para empresas como Amazon, UPS o FedEx
- Identificar y responder a ubicaciones criminales en la ciudad.
- Analítica deportiva profesional
- Predecir y prevenir el cibercrimen
El objetivo principal del método K-Means es dividir el conjunto de datos en grupos distinguibles para que los elementos dentro de cada grupo sean similares entre sí.
Aquí hay una representación visual de cómo se ve en la práctica:
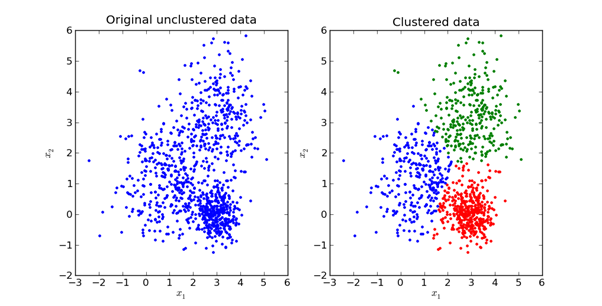
exploraremos las matemáticas detrás del método K-Means en la siguiente sección de este artículo.
¿Cómo funciona el método K-Means?
El primer paso para usar el método K-Means es elegir la cantidad de grupos en los que desea dividir sus datos. Esta cantidad es el valor de K, reflejado en el nombre del algoritmo. La elección del valor K en el método K-Means es muy importante. Discutiremos cómo elegir el valor correcto de K un poco más tarde.
A continuación, debe seleccionar aleatoriamente un punto en el conjunto de datos y asignarlo a un grupo aleatorio. Esto le dará la posición de inicio de datos en la que ejecuta la siguiente iteración hasta que los grupos dejen de cambiar:
- Calcular el centroide (centro de gravedad) de cada grupo tomando el vector medio de puntos en ese grupo
- Reasigne cada punto de datos al grupo cuyo centroide está más cerca del punto
Elección de un valor K apropiado en el método K-medias
Estrictamente hablando, elegir un valor K adecuado es bastante difícil. No hay una respuesta "correcta" al elegir el "mejor" valor de K. Un método que los profesionales de ML suelen utilizar se llama "método del codo".
Para usar este método, lo primero que debe hacer es calcular la suma de los errores al cuadrado: la desviación estándar de su algoritmo para un grupo de valores K. La desviación estándar en el método K-means se define como la suma de los cuadrados de las distancias entre cada punto de datos en el grupo. y el centro de gravedad de este grupo.
Como ejemplo de este paso, puede calcular la desviación estándar para los valores K de 2, 4, 6, 8 y 10. A continuación, querrá generar un gráfico de la desviación estándar y estos valores K. Verá que la desviación disminuye a medida que aumenta el valor K.
Y tiene sentido: cuantas más categorías cree a partir de un conjunto de datos, más probable será que cada punto de datos esté cerca del centro del clúster de ese punto.
Dicho esto, la idea principal detrás del método del codo es elegir el valor K en el que el RMS reducirá drásticamente la tasa de disminución. Este fuerte descenso forma un "codo" en el gráfico.
Como ejemplo, aquí hay una gráfica de RMS en relación con K. En este caso, el método del codo sugerirá usar un valor K de aproximadamente 6.
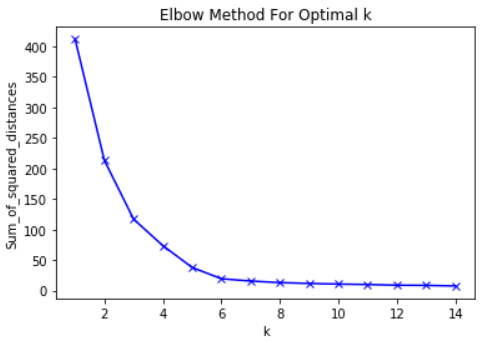
Es importante que K = 6 sea simplemente una estimación de un valor K aceptable. No hay un valor K "mejor" en el método K-Means. Como muchas cosas en ML, esta es una decisión muy situacional.
Resumir
Aquí hay un bosquejo rápido de lo que acaba de aprender en esta sección:
- Ejemplos de tareas de ML sin un maestro que pueden resolverse mediante el método K-means
- Principios básicos del método K-means
- Cómo funciona K-Means
- Cómo usar el método del codo para seleccionar el valor apropiado para el parámetro K en este algoritmo
Análisis de componentes principales
El análisis de componentes principales se usa para transformar un conjunto de datos con muchos parámetros en un nuevo conjunto de datos con menos parámetros, y cada nuevo parámetro en este conjunto de datos es una combinación lineal de parámetros previamente existentes. Estos datos transformados tienden a justificar gran parte de la varianza del conjunto de datos original con mucha más simplicidad.
¿Qué es el método del componente principal?
El análisis de componentes principales (PCA) es una técnica de ML que se utiliza para estudiar las relaciones entre conjuntos de variables. En otras palabras, el PCA examina conjuntos de variables para determinar la estructura básica de estas variables. PCA también se llama a veces análisis factorial.
Según esta descripción, puede pensar que PCA es muy similar a la regresión lineal. Pero este no es el caso. De hecho, estas 2 técnicas tienen varias diferencias importantes.
Diferencias entre regresión lineal y PCA
La regresión lineal determina la línea de mejor ajuste en el conjunto de datos. El análisis de componentes principales identifica múltiples líneas ortogonales de mejor ajuste para un conjunto de datos.
Si no está familiarizado con el término ortogonal, simplemente significa que las líneas están en ángulo recto entre sí, como norte, este, sur y oeste en un mapa.
Veamos un ejemplo para ayudarlo a comprender esto mejor.

Eche un vistazo a las etiquetas de los ejes en esta imagen. El componente principal del eje x explica el 73% de la varianza en este conjunto de datos. El componente principal del eje y explica aproximadamente el 23% de la varianza en el conjunto de datos.
Esto significa que el 4% de la varianza permanece sin explicación. Puede reducir este número agregando más componentes principales a su análisis.
Resumir
Un resumen de lo que acaba de aprender sobre el análisis de componentes principales:
- PCA intenta encontrar factores ortogonales que determinan la variabilidad en un conjunto de datos
- Diferencia entre regresión lineal y PCA
- Cómo se ven los componentes principales ortogonales cuando se procesan en un conjunto de datos
- Que agregar componentes principales adicionales puede ayudar a explicar la varianza con mayor precisión en el conjunto de datos