Las matemáticas a distancia social son una lección de geometría

El desafío de cómo reabrir oficinas, escuelas y otros lugares públicos de manera segura mientras se mantiene a las personas a un metro y medio de distancia se reduce a una pregunta que los matemáticos han estado estudiando durante siglos.

Puede parecer que un tema como el empaquetamiento de esferas atraerá solo a los matemáticos. ¿Quién más estaría interesado en buscar las formas más efectivas de colocar círculos en un plano o esferas en el espacio?



Sin embargo, hoy millones de personas en todo el mundo están reflexionando precisamente sobre esta tarea.



Determinar cómo abrir edificios y espacios públicos de manera segura mientras se mantiene una distancia social es, en particular, un ejercicio de geometría. Si cada persona debe estar al menos a un metro y medio de distancia de otras personas, entonces para calcular cuántas personas pueden sentarse en el salón de clases o el comedor, debe incluir círculos que no se superpongan en el plano del piso.







Naturalmente, para combatir el coronavirus, es necesario resolver muchos más problemas que este geométrico. Sin embargo, el empaquetamiento de círculos y esferas juega un papel en esto, al igual que el modelado de estructuras cristalinas en química y espacios de mensajes abstractos en la teoría de la información. Esta tarea, aparentemente simple en la descripción, ha ocupado las mentes de los más grandes matemáticos de la historia, y la investigación más interesante en esta área se está llevando a cabo hoy, en particular, en dimensiones superiores. Por ejemplo, los matemáticos encontraron recientemente la mejor manera de empaquetar en espacios de 8 y 24 dimensiones, una técnica necesaria para optimizar los códigos de corrección de errores utilizados tanto en teléfonos celulares como en la comunicación con sondas espaciales. Entonces, echemos un vistazo a algunas de las complicaciones inesperadas que surgen cuando intentamos llenar un espacio con la forma más simple.



Ya sea que esté empacando naranjas en cajas en el trabajo o sentando de manera segura a los estudiantes con distanciamiento social, el tamaño y la forma de su contenedor es fundamental para su tarea. Sin embargo, para la mayoría de los matemáticos, la teoría del empaquetamiento de esferas trata de llenar todo el espacio. En dos dimensiones, esto significa cubrir el plano con círculos disjuntos del mismo tamaño.



Aquí hay un ejemplo de círculos de embalaje en un avión. Parece una vista superior de un paquete de refrescos:







Puedes imaginar cómo este patrón se repite en todas las direcciones, como una baldosa pavimentada con un plano. Pequeños espacios entre círculos indican que el avión no está completamente lleno, pero en el caso de círculos de empaque, esto debería ser de esperar. Nos interesa saber qué porcentaje del avión está cubierto. Esta será la "densidad de empaquetamiento" del método en particular.



El método anterior se llama empaque cuadrado y por una buena razón: los centros de los círculos se pueden representar como los vértices de los cuadrados.







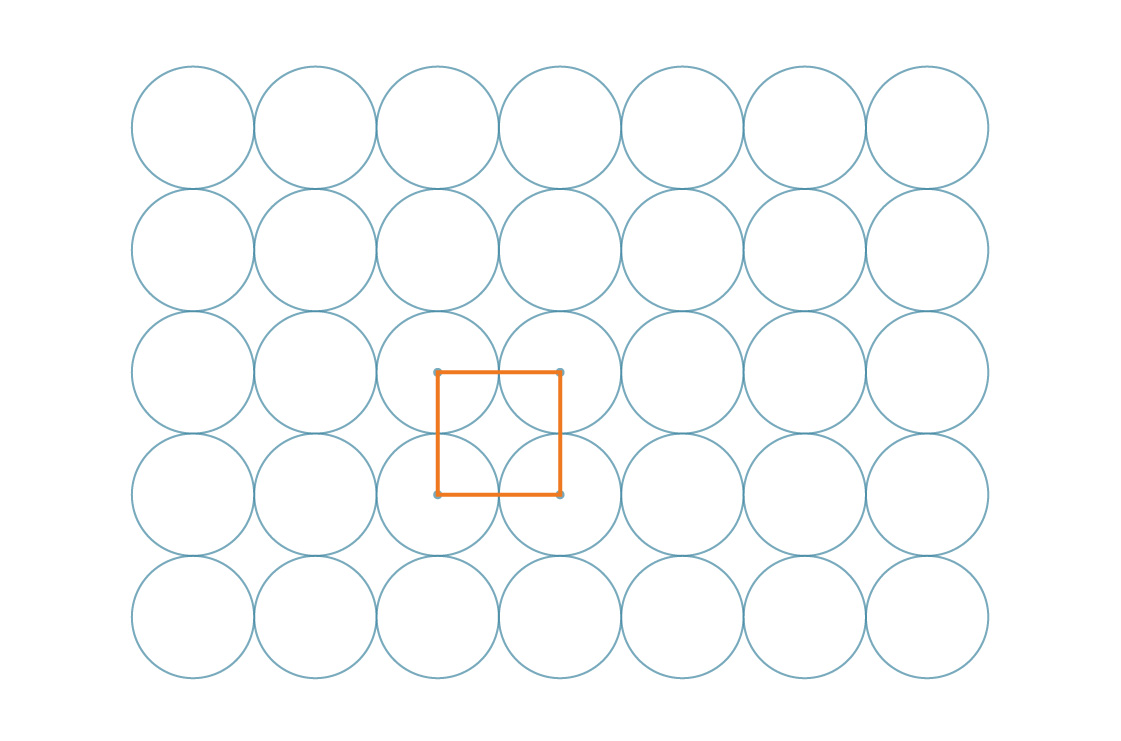
Y, de hecho, estos mismos cuadrados embaldosan el plano:







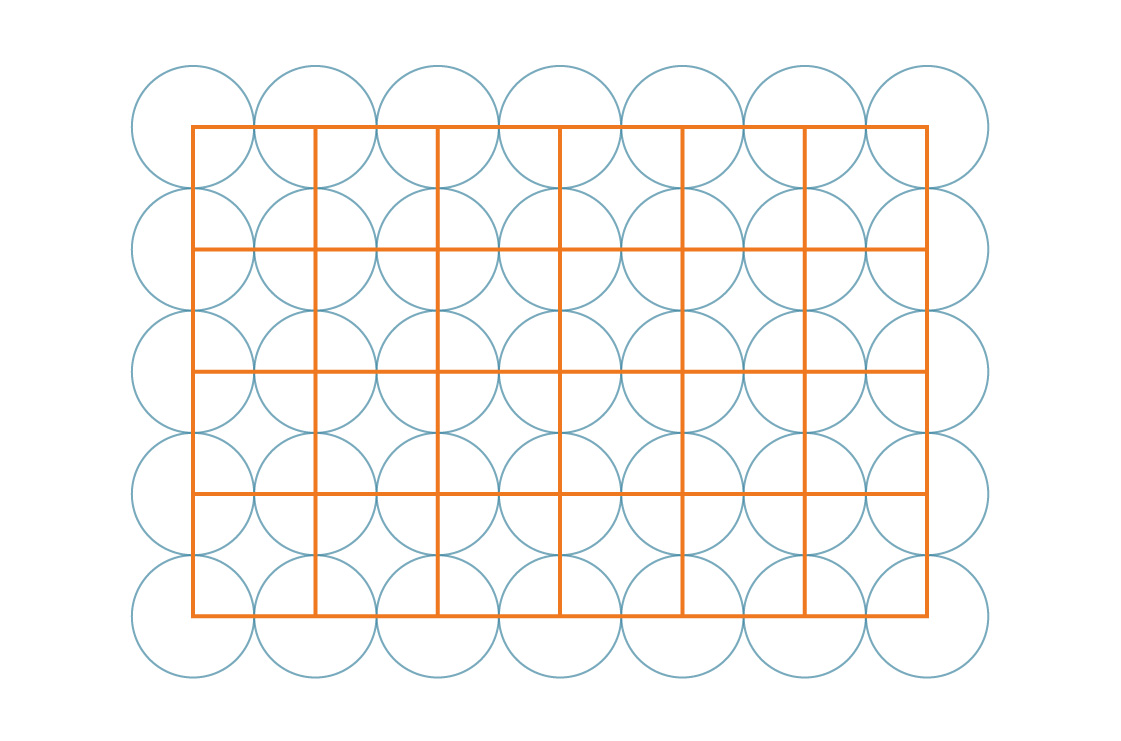
nuestra tarea se ve facilitada por la simetría del patrón. Dado que estos cuadrados cubren todo el plano de manera periódica, el porcentaje del plano cubierto por los círculos es el mismo que el porcentaje del cuadrado cubierto por los círculos. Veamos uno de estos cuadrados.







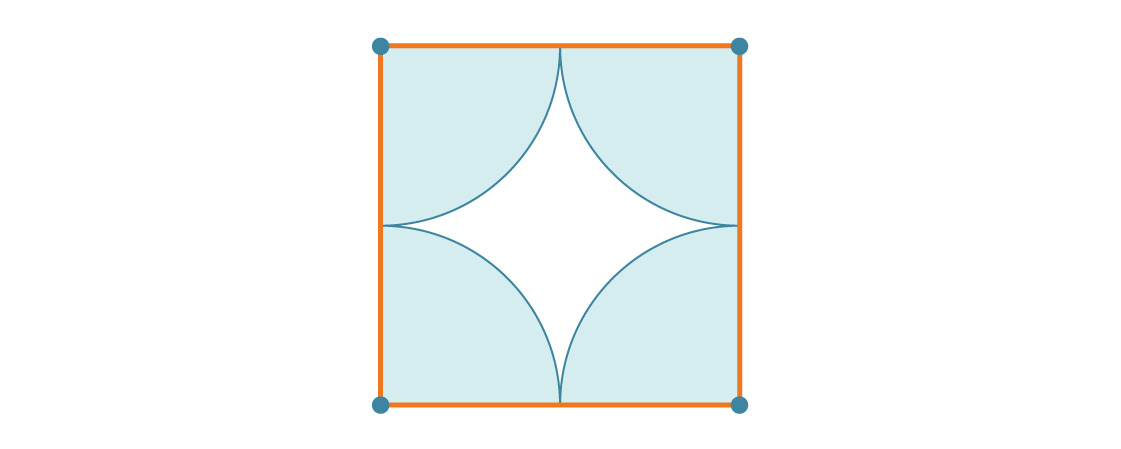
Digamos que el radio del círculo es r. Esto significa que la longitud del lado del cuadrado es 2r. En cada uno de los vértices del cuadrado hay un cuarto de círculo, por lo que el porcentaje de cobertura de cada cuadrado es simplemente igual a la relación entre el área de un círculo completo y el área de un cuadrado completo:

$$

$$\frac{\pi r^2}{(2r)^2} = \frac{\pi r^2}{4r^2} = \frac{\pi }{4} \approx 0,7854$$

Cada cuadrado tiene aproximadamente un 78,54% cubierto de círculos, por lo que, considerando el mosaico del avión, todo está aproximadamente un 78,54% cubierto de círculos. Ésta es la densidad del empaque cuadrado. Observe que el radio r desapareció de la respuesta. Y esto tiene sentido: no importa el tamaño de los círculos, todavía habrá cuatro cuartos de círculo en un cuadrado.



Si trataste de doblar las latas de refresco por los lados de esta manera, y se deslizan y llenan los huecos, sabes que hay otra forma de empaquetar los círculos en un plano:







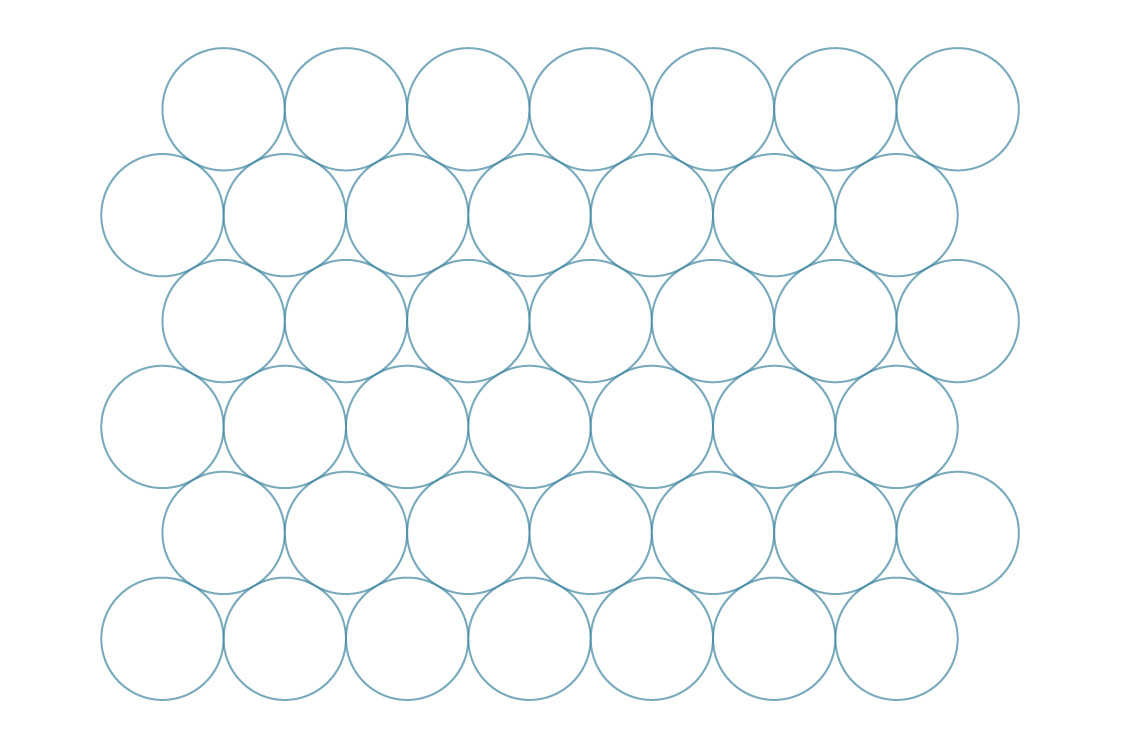
tomemos un enfoque similar al anterior, e imaginemos que los centros de los círculos en este caso forman hexágonos regulares. ...







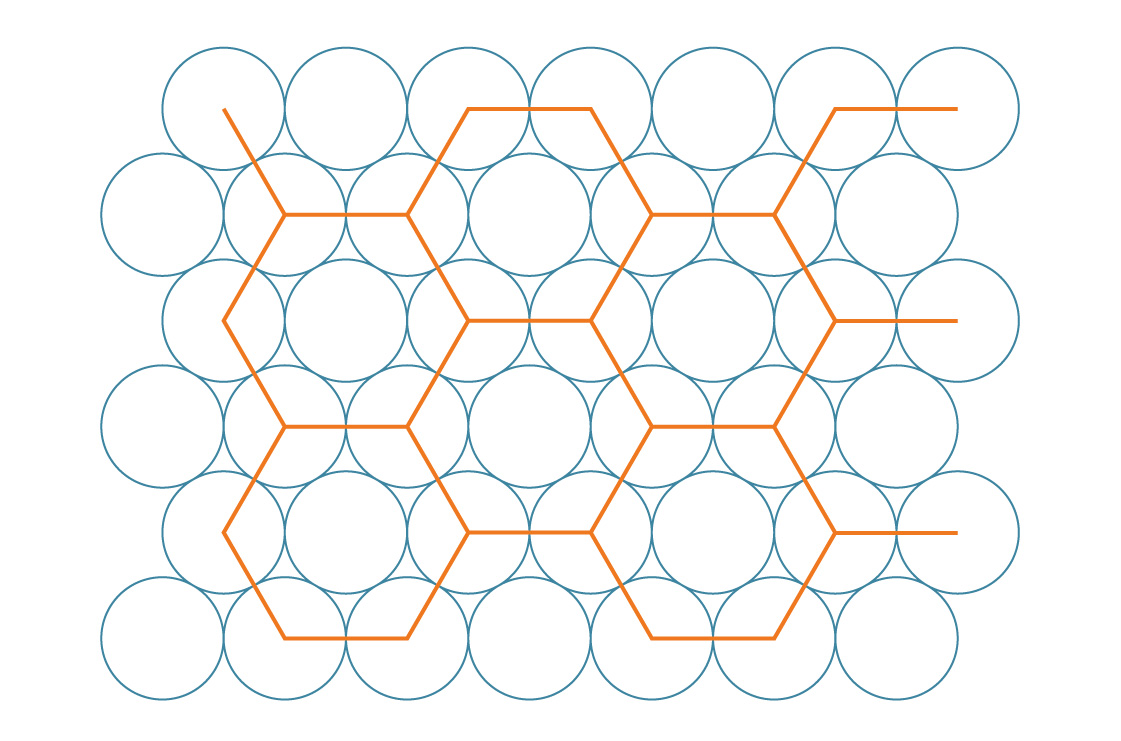
A esto lo llamamos empaque hexagonal. Parece que este método llena los huecos más eficazmente que el cuadrado. Para comprobar esto, comparemos sus densidades de empaque. Los hexágonos, como los cuadrados, recubren completamente el plano, por lo que podemos determinar la densidad de este método analizando un solo hexágono.







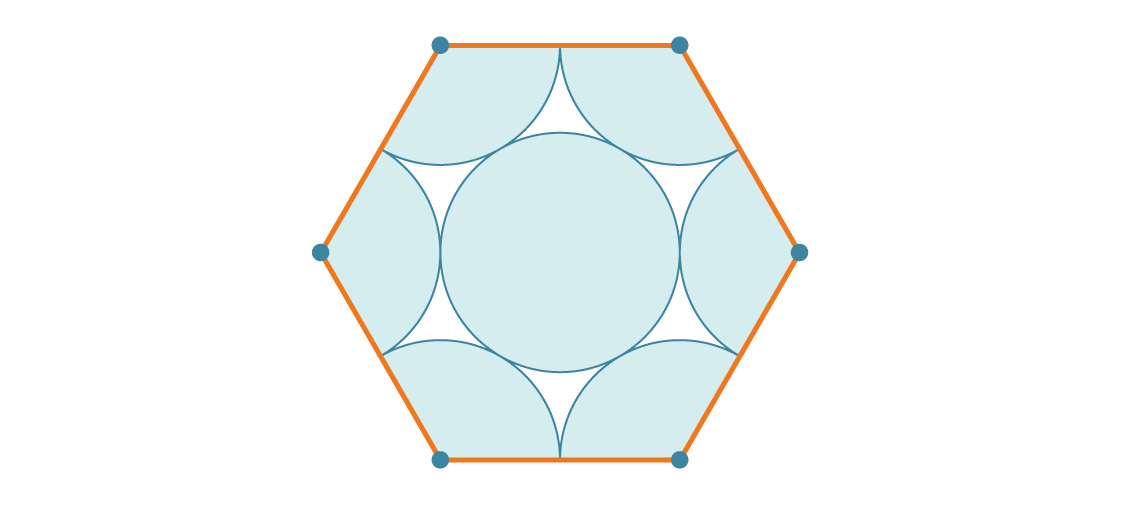
¿Qué parte del hexágono está cubierta de círculos? Dado que un hexágono regular tiene un ángulo interno de 120 °, hay un tercio de un círculo en cada una de las esquinas. Resultan dos círculos completos, y el círculo del medio va tercero. Por lo tanto, cada hexágono está cubierto por tres círculos. Si el radio de cada círculo es r, entonces el área es 3πr².







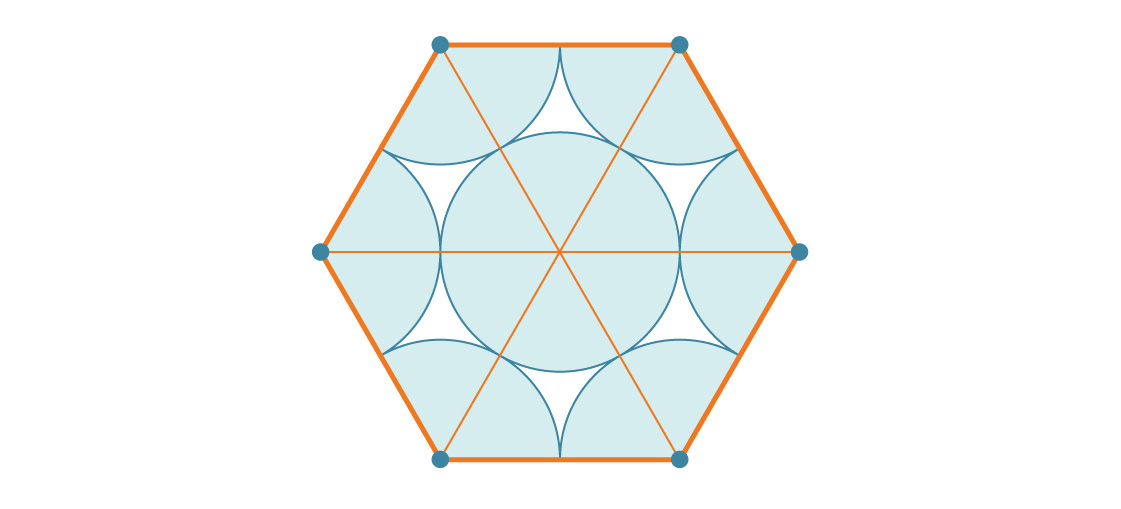
¿Cómo se compara esto con el área de un hexágono? Un hexágono con una longitud de lado s es seis triángulos equiláteros con una longitud de lado s, cada uno de los cuales es s ² √3 / 4. Por lo tanto, el área del hexágono es 6 * s ² √3 / 4 = 6 s ² √3 / 4. Dado que la longitud del lado de nuestro hexágono es 2r, su área es:

$$

$$\frac{6 s^2 \sqrt3}{4} = \frac{6 (2r)^2 \sqrt3}{4} = \frac{24 r^2 \sqrt3}{4} = 6 r^2 \sqrt3$$

Ahora puede calcular el porcentaje del hexágono cubierto por los círculos (dividiendo el área de los seis círculos por el área del hexágono):

$$

$$\frac{3 \pi r^2}{6 r^2 \sqrt3} = \frac{3 \pi}{6 \sqrt3} = \frac{\pi}{2 \sqrt3} \approx 0,9069$$

Cada hexágono está cubierto en un 90,69% con círculos, por lo que este envase será mucho más eficiente que uno cuadrado. Observe cómo el radio del círculo desaparece nuevamente como se esperaba. De hecho, no existe un embalaje más eficiente.



Pero no fue fácil demostrarlo. Famosos matemáticos como Joseph Louis Lagrange y Karl Friedrich Gauss comenzaron a trabajar en esto a fines del siglo XVIII y principios del XIX, pero el problema se resolvió por completo solo en la década de 1940, procesando cuidadosamente todos los arreglos posibles, periódicos y no periódicos. El hecho de que haya tardado tanto en resolver el problema en dos dimensiones, donde todo es bastante fácil de imaginar, puede servir como una advertencia de lo que nos espera en dimensiones superiores.



Empacar esferas en tres dimensiones es una tarea mucho más difícil, aunque tiene algunas similitudes con su primo bidimensional. Por ejemplo, los empaques bidimensionales que hemos considerado constan de una capa.







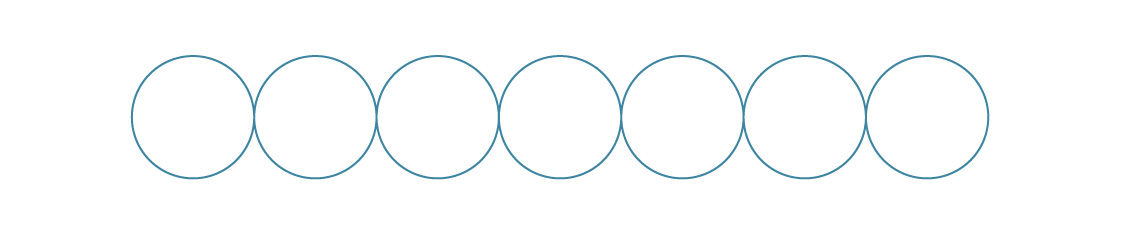
Para un paquete cuadrado, colocamos cada capa encima de la anterior.







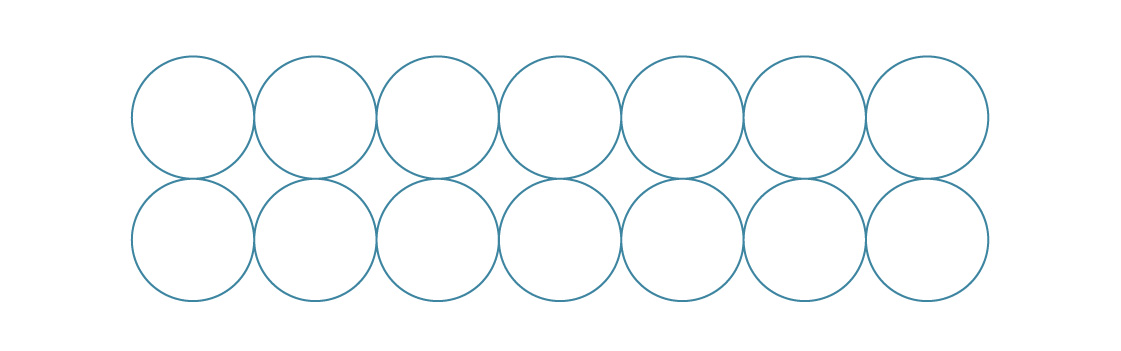
Para el empaque hexagonal, colocamos nuevas capas entre las anteriores.







Se obtienen diferentes envases dependiendo de cómo combinemos copias de diferentes capas.



En tres dimensiones, esta disposición de capas una encima de la otra crea empaquetaduras fundamentalmente diferentes.







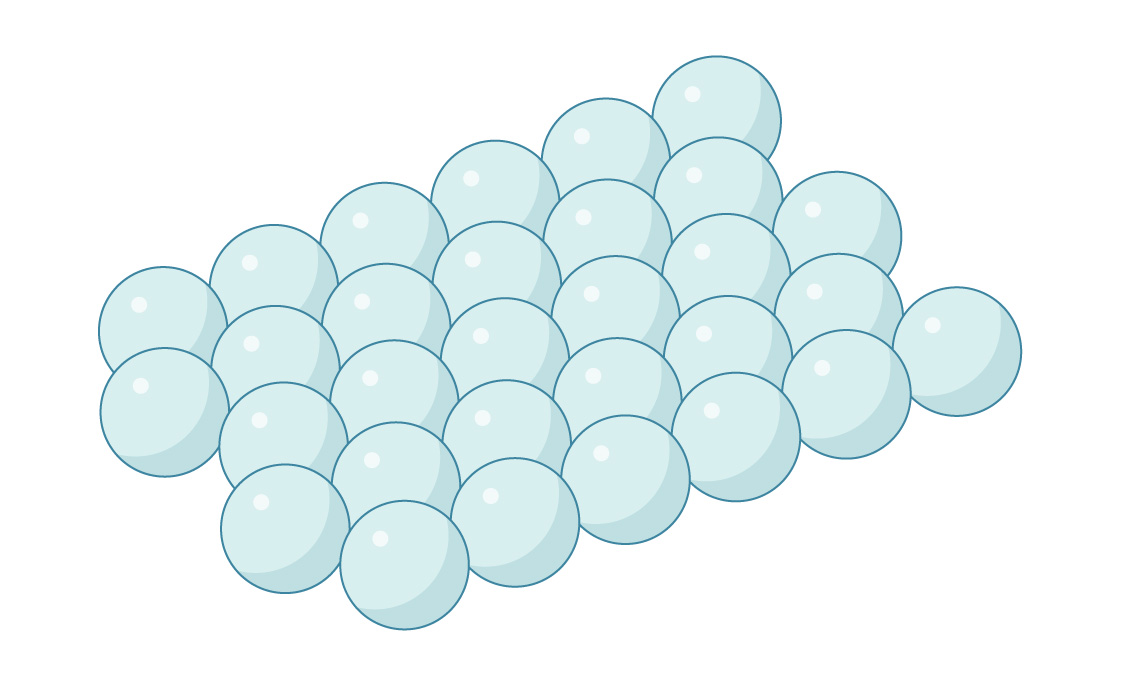
Esta es una capa de esferas empaquetadas hexagonalmente, como sugiere nuestro empaque óptimo de círculos en un plano. Asimismo, puede colocar la segunda capa encima de la primera colocando esferas en los espacios entre las esferas inferiores.







Pero en tres dimensiones, la geometría se vuelve un poco más complicada. En cada capa de esferas, la distancia entre huecos adyacentes resulta ser menor que la distancia entre los centros de las esferas. Por lo tanto, no puede colocar una esfera en cada espacio: se cruzarían. Por lo tanto, los espacios en las dos capas se alinean, creando canales que atraviesan el paquete.







Hay dos formas de colocar la tercera capa. Puede alinear los espacios con los inferiores y dejar los canales abiertos. A continuación se muestra una vista lateral de esta disposición:







para mantener los canales abiertos, debe colocar las esferas en la tercera capa justo encima de las esferas de la primera capa. Esta disposición de esferas se llama "empaquetadura densa hexagonal" (silo), y si lo mira desde arriba, puede ver espacios abiertos que la atraviesan.







Otra opción para colocar la tercera capa es cerrar los canales. Las esferas de la tercera capa se colocan directamente sobre los huecos de la primera:







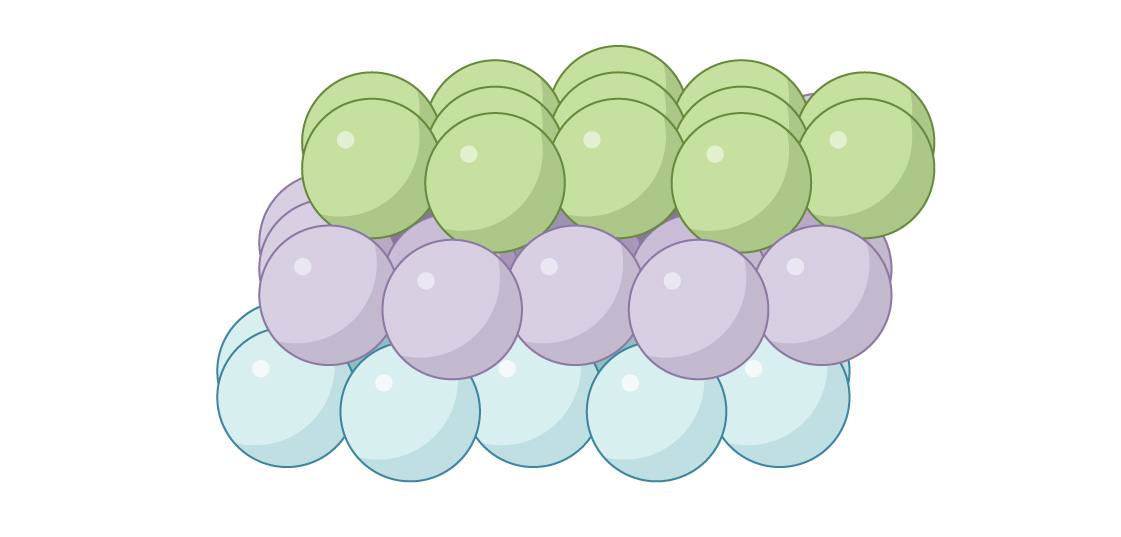
esto se denomina "cúbico centrado en la cara" (FCC) o "empaque cerrado cúbico". Cuando se ve desde arriba, no habrá espacios.







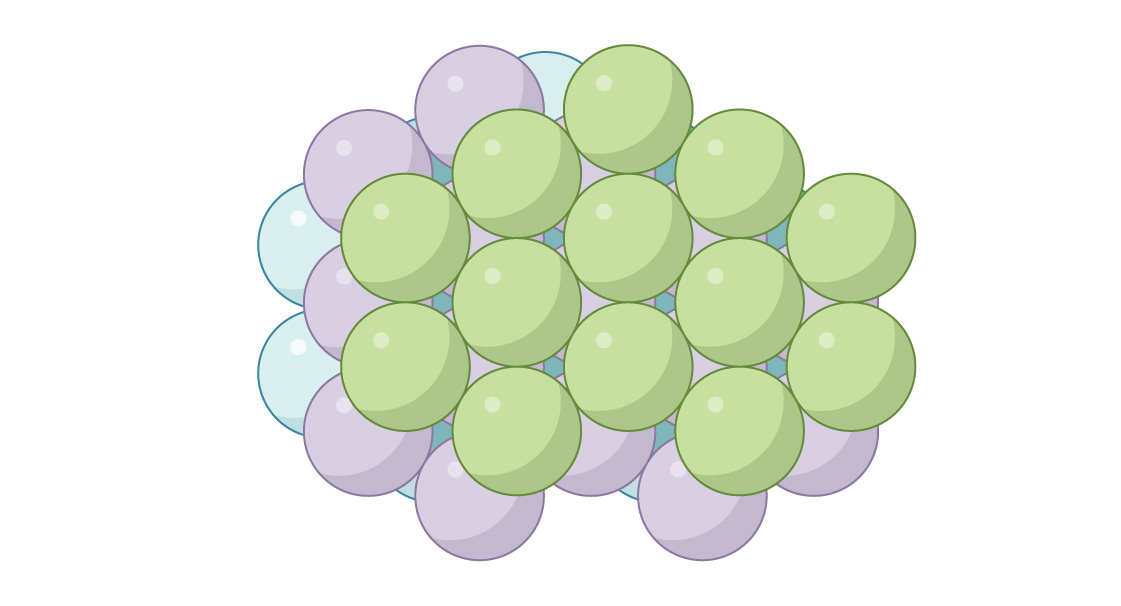
Estos dos arreglos similares pero fundamentalmente diferentes surgen en química y describen el arreglo de átomos en diferentes materiales. Por ejemplo, en metales como la plata y el oro, la estructura tiene la forma de HA, y en metales como el zinc y el titanio, los silos. Cada uno de los dos métodos le permite llenar el espacio con esferas. En el método del silo, en cada segunda capa, las esferas se ubican exactamente igual, y en el GK, en cada tercio. Puede crear un número infinito de paquetes diferentes combinando ambos métodos, ¡pero es interesante que tanto silo como GK brinden un empaque óptimo! Su densidad de empaquetamiento no solo es la misma, π 3√2 ≈ 0.7405 es el empaquetamiento más denso posible en el espacio tridimensional. El famoso matemático y astrónomo Johannes Kepler sugirió esto en 1611, pero prueba completasolo el matemático Thomas Hales pudo deducir en 1998.







Hay más espacio en el espacio 3D y tenemos más formas de empaquetar las esferas de manera efectiva. Cuando agrega dimensiones, la complejidad del empaque solo aumenta: hay más espacio, más opciones y es más difícil de imaginar. Además, las esferas se vuelven más pequeñas en dimensiones más altas.







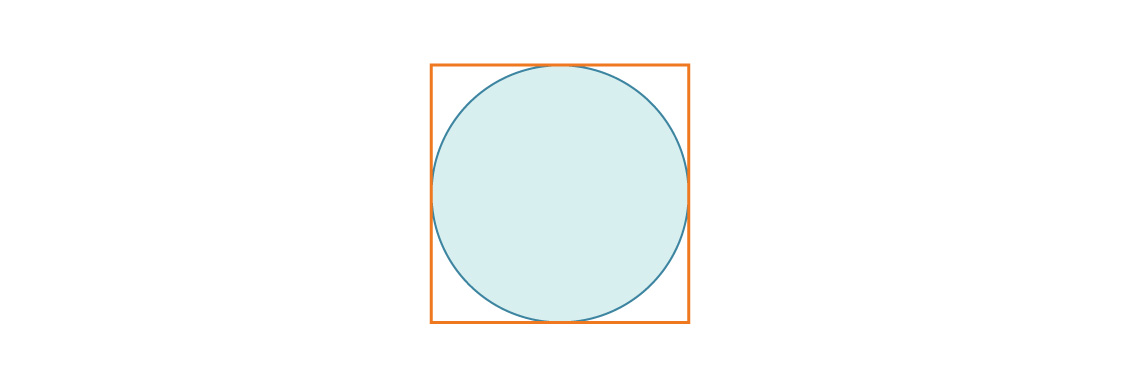
Considere un círculo inscrito en un cuadrado con una longitud de lado 1.



El radio del círculo es r = 1/2, por lo que la razón entre el área del círculo y el área del cuadrado es:

$$

$$\frac{\pi r^2}{s^2} = \frac{\pi (\frac{1}{2})^2}{1^2} = \frac{\pi }{4} \approx 0,7854$$

Lo cual también es igual a la densidad de empaque del cuadrado en dos dimensiones.



Ahora consideremos el volumen de una esfera inscrita en un cubo unitario.







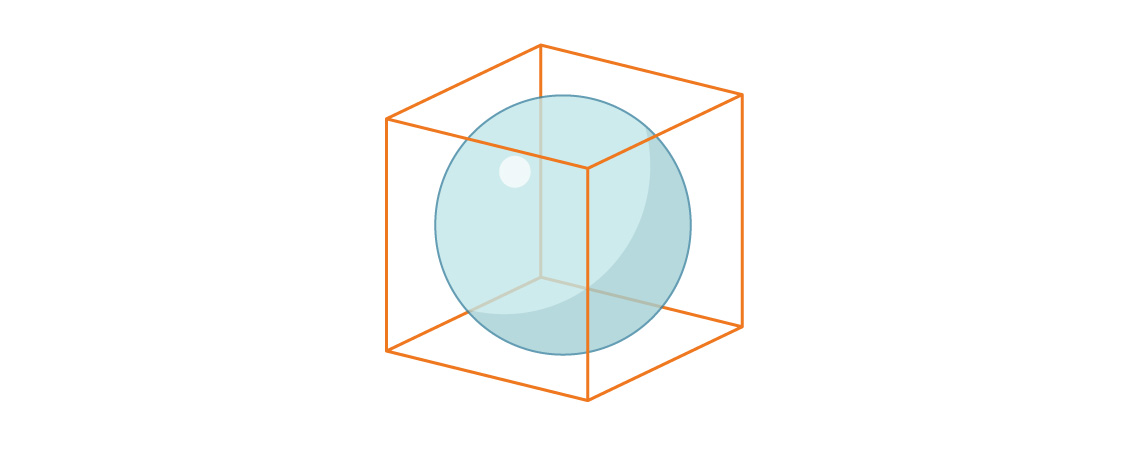
El radio de la esfera es nuevamente igual a r = 1/2, por lo que la relación entre el volumen de la esfera y el volumen del cubo es:

$$

$$\frac{\frac{4}{3}\pi r^3}{s^3} = \frac{\frac{4}{3}\pi (\frac{1}{2})^3}{1^3} = \frac{4}{3}\pi (\frac{1}{8}) = \frac{\pi}{6} \approx 0,5236$$

Tenga en cuenta que la proporción del cubo ocupado por la esfera inscrita en tres dimensiones es menor que la proporción del cuadrado ocupado por el círculo inscrito en dos dimensiones. Este patrón continúa: al aumentar las dimensiones, esta relación disminuye. A medida que n crece, las esferas de n dimensiones ocupan cada vez menos espacio de n dimensiones.



Esto se puede demostrar usando álgebra, pero también se puede entender si se piensa en ángulos. En cualquier dimensión, una esfera de n dimensiones se puede inscribir en un cubo de n dimensiones. La esfera toca los bordes del cubo pero no llega a las esquinas, por lo que hay una región alrededor de cada esquina que está dentro del cubo pero fuera de la esfera. Sin embargo, una caja n-dimensional tendrá 2 ⁿángulos, es decir, con un aumento de n, el número de áreas no cubiertas por una esfera crece exponencialmente. Además, la distancia entre las esquinas y la esfera también aumenta. Esto significa que, a la larga, el espacio dentro del cubo n-dimensional, pero fuera de la esfera n-dimensional, simplemente aplastará el espacio ocupado por la esfera.



Si la contracción de las esferas le parece lo suficientemente extraña, entonces los matemáticos involucrados en el empaque de esferas notaron algo aún más inesperado en las dimensiones 8 y 24. En estas dimensiones, las esferas se encogen lo suficiente para poder llenar los espacios entre las nuevas esferas, lo que da un empaque ultradenso en estas dimensiones. ... Se planteó una hipótesis sobre la optimalidad de estos métodos especiales, pero no se conoció exactamente hasta 2016, cuando Marina Vyazovskaya demostró este teorema.para espacio de 8 dimensiones. Una semana después, Vyazovskaya y sus asistentes expandieron su método para probar también el caso del espacio de 24 dimensiones.



Del trabajo de Vyazovskaya se desprende que ahora conocemos las formas más eficientes de empaquetar esferas en las dimensiones 1, 2, 3, 8 y 24. Pero en otras dimensiones todavía hay mucho trabajo por hacer. Así que saca las latas de naranjas y refrescos y empieza a experimentar. Puede que sea usted quien pueda llenar los vacíos importantes.

Ejercicios

1. Digamos que comenzamos a empaquetar el plano de coordenadas como se muestra en las imágenes a continuación. El centro del círculo inferior izquierdo está ubicado en el punto (0, 0) y el centro del círculo inferior derecho está en el punto (2, 0).







¿Dónde está el centro del tercer círculo?



2. A continuación se muestra el comienzo del empaquetado "cúbico simple" de esferas. ¿Cuál es la densidad de empaquetamiento de tal esquema?







3. Aquí está el comienzo de empaquetar el avión en octágonos regulares.







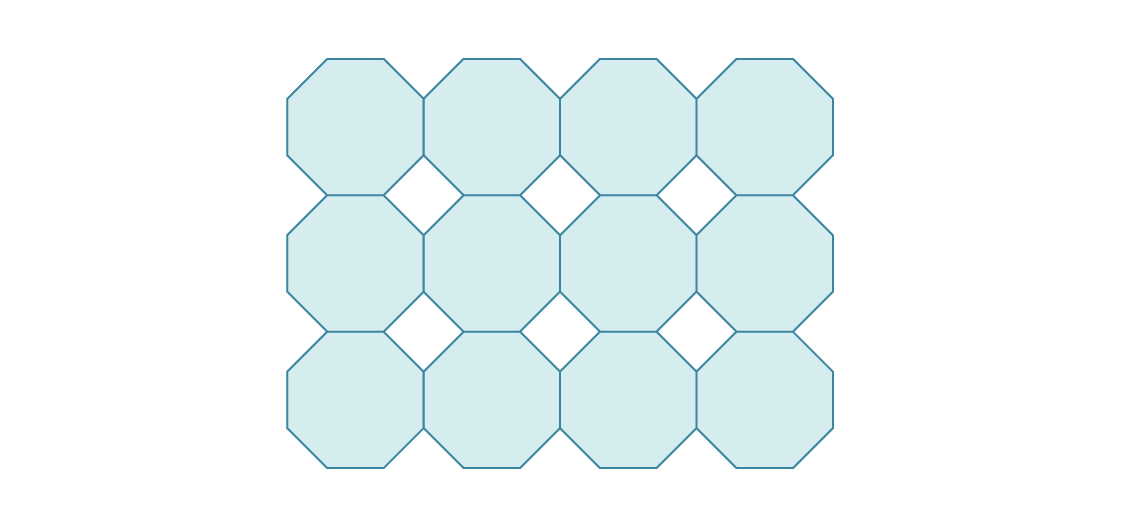
¿Cuál es la densidad de tal paquete?

Respuestas

Ver también:

• " Google lanza Sodar, una herramienta de RA para mostrar la distancia social "
• "El metaestudio revela la efectividad de las máscaras y el distanciamiento contra el SARS-CoV-2 (COVID-19) "
• " COVID-19: Modelo de predicción paramétrica de epidemias "