
Hola a todos, hoy nos ocuparemos del algoritmo de compresión JPEG. Mucha gente no sabe que JPEG no es tanto un formato como un algoritmo. La mayoría de las imágenes JPEG que ve están en JFIF (formato de intercambio de archivos JPEG), dentro del cual se aplica el algoritmo de compresión JPEG. Al final del artículo, comprenderá mucho mejor cómo este algoritmo comprime los datos y cómo escribir código de descompresión en Python. No consideraremos todos los matices del formato JPEG (por ejemplo, escaneo progresivo), pero solo hablaremos sobre las capacidades básicas del formato mientras escribimos nuestro propio decodificador.
Introducción
¿Por qué escribir otro artículo en JPEG cuando ya se han escrito cientos de artículos sobre él? Por lo general, en tales artículos, los autores solo hablan sobre cuál es el formato. No escribe código de desempaquetado y decodificación. Y si escribe algo, estará en C / C ++, y este código no estará disponible para una amplia gama de personas. Quiero romper esta tradición y mostrarte con Python 3 cómo funciona un decodificador JPEG básico. Se basará en este código desarrollado por MIT, pero lo cambiaré mucho en aras de la legibilidad y la claridad. Puede encontrar el código modificado para este artículo en mi repositorio .
Diferentes partes de JPEG
Comencemos con una imagen realizada por Ange Albertini . Enumera todas las partes de un archivo JPEG simple. Analizaremos cada segmento y, a medida que lea el artículo, volverá a esta ilustración más de una vez.
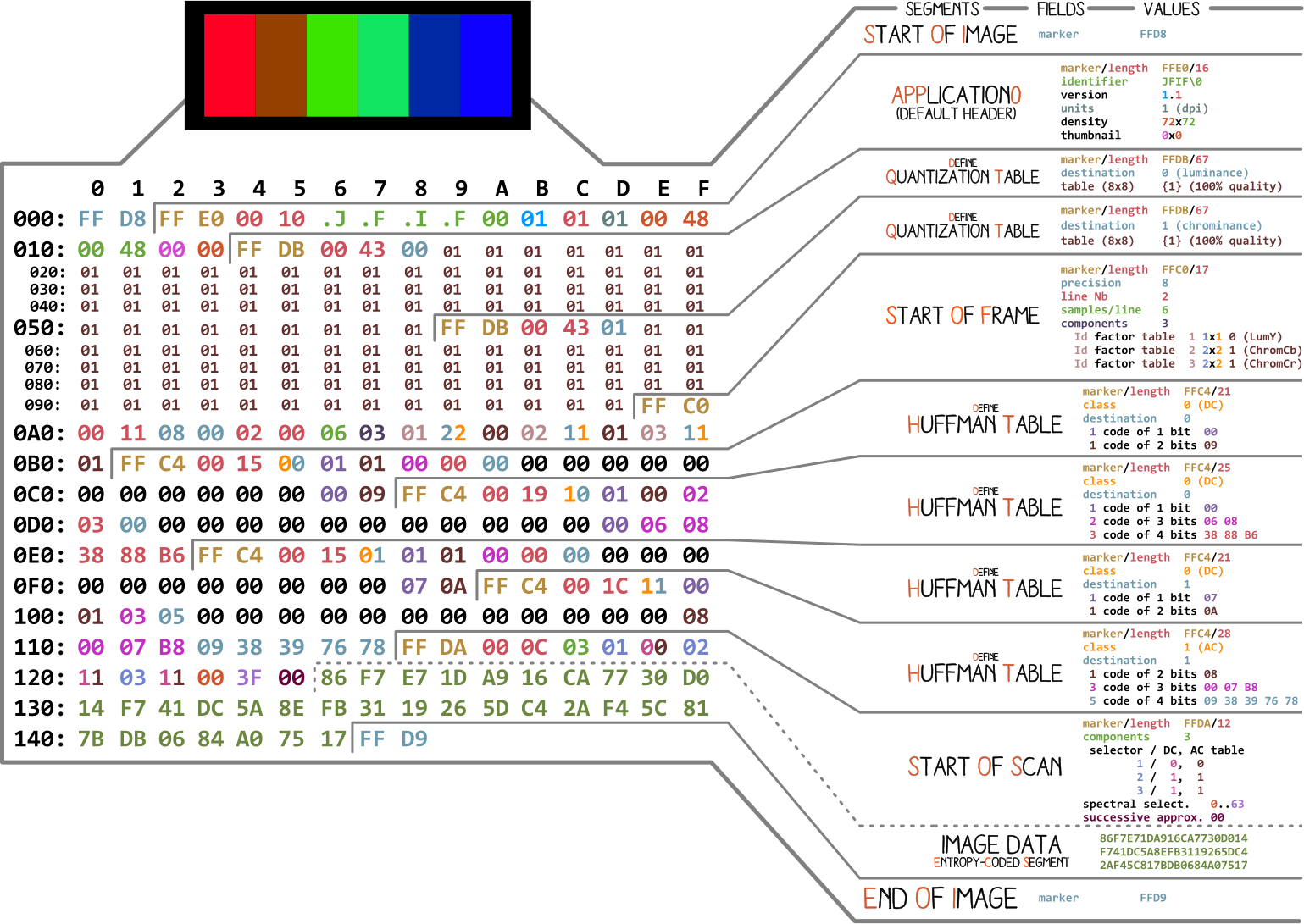
Casi todos los archivos binarios contienen varios marcadores (o encabezados). Puede pensar en ellos como una especie de marcadores. Son esenciales para trabajar con el archivo y son utilizados por programas como file (en Mac y Linux) para que podamos conocer los detalles del archivo. Los marcadores indican exactamente dónde se almacena cierta información en el archivo. La mayoría de las veces, los marcadores se colocan de acuerdo con el valor de longitud (
length) de un segmento en particular.
Inicio y final de archivo
El primer marcador importante para nosotros es
FF D8. Define el comienzo de la imagen. Si no lo encontramos, entonces podemos asumir que el marcador está en algún otro archivo. El marcador no es menos importante FF D9. Dice que hemos llegado al final del archivo de imagen. Después de cada marcador, con la excepción del rango FFD0- FFD9e FF01, inmediatamente viene el valor de la longitud del segmento de este marcador. Y los marcadores del principio y el final del archivo siempre tienen dos bytes de longitud.
Trabajaremos con esta imagen:

Escribamos un código para encontrar los marcadores de inicio y finalización.
from struct import unpack
marker_mapping = {
0xffd8: "Start of Image",
0xffe0: "Application Default Header",
0xffdb: "Quantization Table",
0xffc0: "Start of Frame",
0xffc4: "Define Huffman Table",
0xffda: "Start of Scan",
0xffd9: "End of Image"
}
class JPEG:
def __init__(self, image_file):
with open(image_file, 'rb') as f:
self.img_data = f.read()
def decode(self):
data = self.img_data
while(True):
marker, = unpack(">H", data[0:2])
print(marker_mapping.get(marker))
if marker == 0xffd8:
data = data[2:]
elif marker == 0xffd9:
return
elif marker == 0xffda:
data = data[-2:]
else:
lenchunk, = unpack(">H", data[2:4])
data = data[2+lenchunk:]
if len(data)==0:
break
if __name__ == "__main__":
img = JPEG('profile.jpg')
img.decode()
# OUTPUT:
# Start of Image
# Application Default Header
# Quantization Table
# Quantization Table
# Start of Frame
# Huffman Table
# Huffman Table
# Huffman Table
# Huffman Table
# Start of Scan
# End of Image
Para descomprimir los bytes de la imagen, usamos struct .
>Hle dice structque lea el tipo de datos unsigned shorty trabaje con él en orden de mayor a menor (big-endian). Los datos JPEG se almacenan en el formato de mayor a menor. Solo los datos EXIF pueden estar en formato little-endian (aunque normalmente no es el caso). Y el tamaño shortes 2, por lo que transferimos unpackdos bytes de img_data. ¿Cómo supimos qué es short? Sabemos que los marcadores están en JPEG se indican con cuatro caracteres hexadecimales: ffd8. Uno de esos caracteres equivale a cuatro bits (medio byte), por lo que cuatro caracteres serán equivalentes a dos bytes, como short.
Después de la sección Inicio de escaneo, siguen inmediatamente los datos de la imagen escaneada, que no tiene una longitud específica. Continúan hasta el final del marcador de archivo, por lo que por ahora lo "buscamos" manualmente cuando encontramos el marcador de Inicio de escaneo.
Ahora tratemos con el resto de los datos de la imagen. Para hacer esto, primero estudiamos la teoría y luego pasamos a la programación.
Codificación JPEG
Primero, hablemos de los conceptos básicos y las técnicas de codificación que se utilizan en JPEG. Y la codificación se realizará en orden inverso. En mi experiencia, la decodificación será difícil de descifrar sin ella.
La siguiente ilustración aún no es clara para usted, pero le daré sugerencias a medida que aprenda el proceso de codificación y decodificación. Estos son los pasos para la codificación JPEG ( fuente ):
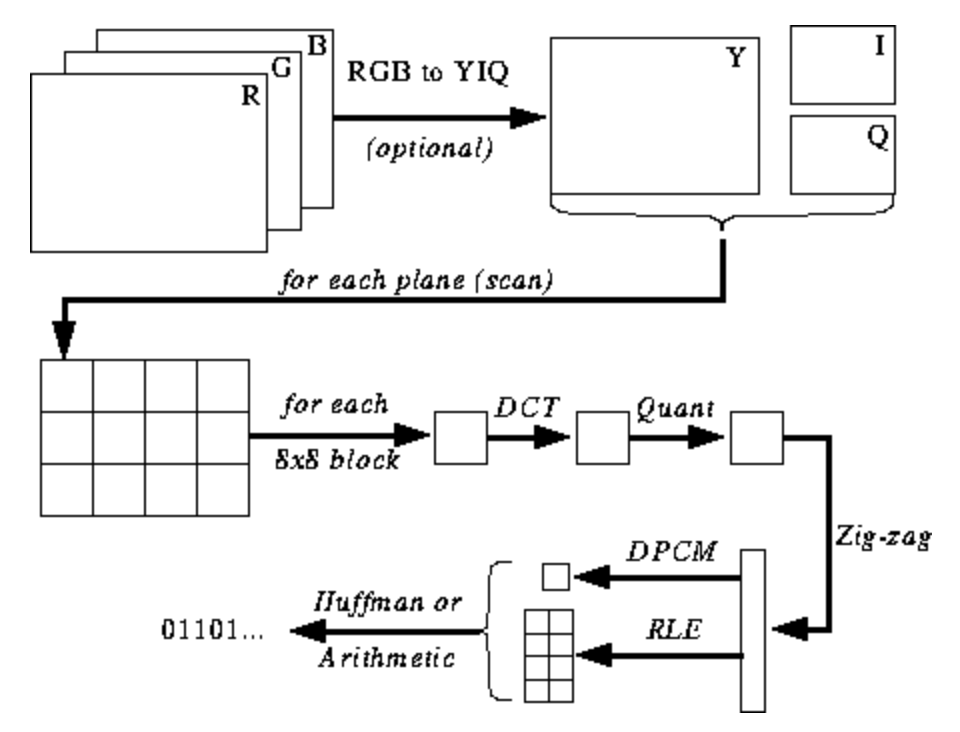
Espacio de color JPEG
Según la especificación JPEG ( ISO / IEC 10918-6: 2013 (E) Sección 6.1):
- Las imágenes codificadas con un solo componente se tratan como datos en escala de grises, donde 0 es negro y 255 es blanco.
- Las imágenes codificadas con tres componentes se consideran datos RGB codificados en el espacio YCbCr. Si la imagen contiene el segmento de marcador APP14 descrito en la Sección 6.5.3, entonces la codificación de color se considera RGB o YCbCr de acuerdo con la información del segmento de marcador APP14. La relación entre RGB y YCbCr se define de acuerdo con UIT-T T.871 | ISO / IEC 10918-5.
- , , CMYK-, (0,0,0,0) . APP14, 6.5.3, CMYK YCCK APP14. CMYK YCCK 7.
La mayoría de las implementaciones del algoritmo JPEG utilizan luminancia y crominancia (codificación YUV) en lugar de RGB. Esto es muy útil porque el ojo humano es muy deficiente para distinguir cambios de alta frecuencia en el brillo en áreas pequeñas, por lo que puede reducir la frecuencia y la persona no notará la diferencia. ¿Qué hace? Imagen muy comprimida con degradación de la calidad casi imperceptible.
Al igual que en RGB, cada píxel está codificado con tres bytes de colores (rojo, verde y azul), por lo que en YUV se utilizan tres bytes, pero su significado es diferente. El componente Y define el brillo del color (luminancia o luma). U y V definen el color (croma): U es responsable de la porción de azul y V - de la porción de rojo.
Este formato se desarrolló en un momento en que la televisión aún no era tan común, y los ingenieros querían utilizar el mismo formato de codificación de imágenes para la transmisión de televisión en color y en blanco y negro. Lea más sobre esto aquí .
Transformada discreta de coseno y cuantificación
JPEG convierte la imagen en bloques de píxeles de 8x8 (llamados MCU, Unidad de codificación mínima), cambia el rango de valores de píxeles para que el centro sea 0, luego aplica una transformada de coseno discreta a cada bloque y comprime el resultado mediante cuantificación. Veamos qué significa todo esto.
La transformada de coseno discreta (DCT) es un método para transformar datos discretos en combinaciones de ondas de coseno. Convertir una imagen en un conjunto de cosenos parece una pérdida de tiempo a primera vista, pero comprenderá el motivo cuando aprenda los siguientes pasos. DCT toma un bloque de 8x8 píxeles y nos dice cómo reproducir ese bloque usando una matriz de funciones de coseno de 8x8. Más detalles aquí .
La matriz se ve así:

Aplicamos DCT por separado a cada componente de píxel. Como resultado, obtenemos una matriz de coeficientes de 8x8, que muestra la contribución de cada (de las 64) funciones de coseno en la matriz de entrada de 8x8. En la matriz de coeficientes DCT, los valores más grandes suelen estar en la esquina superior izquierda y los más pequeños en la esquina inferior derecha. La parte superior izquierda es la función de coseno de frecuencia más baja y la parte inferior derecha es la más alta.
Esto significa que en la mayoría de las imágenes hay una gran cantidad de información de baja frecuencia y una pequeña proporción de información de alta frecuencia. Si a los componentes inferiores a la derecha de cada matriz DCT se les asigna un valor de 0, entonces la imagen resultante se verá igual para nosotros, porque una persona no distingue mal los cambios de alta frecuencia. Esto es lo que haremos en el siguiente paso.
Encontré un gran video sobre este tema. Mire si no comprende el significado de PrEP:
Todos sabemos que JPEG es un algoritmo de compresión con pérdida. Pero hasta ahora no hemos perdido nada. Solo tenemos bloques de componentes 8x8 YUV convertidos en bloques de funciones coseno 8x8 sin pérdida de información. La etapa de pérdida de datos es la cuantificación.
La cuantificación es el proceso en el que tomamos dos valores de un cierto rango y los convertimos en un valor discreto. En nuestro caso, este es solo un nombre astuto para reducir a 0 los coeficientes de frecuencia más altos en la matriz DCT resultante. Al guardar una imagen con JPEG, la mayoría de los editores de gráficos le preguntan qué nivel de compresión desea establecer. Aquí es donde ocurre la pérdida de información de alta frecuencia. Ya no podrá volver a crear la imagen original a partir de la imagen JPEG resultante.
Se utilizan diferentes matrices de cuantificación en función de la relación de compresión (dato curioso: la mayoría de los desarrolladores tienen patentes para crear una tabla de cuantificación). Dividimos la matriz DCT de coeficientes elemento por elemento por la matriz de cuantificación, redondeamos los resultados a números enteros y obtenemos la matriz cuantificada.
Veamos un ejemplo. Digamos que existe tal matriz DCT:

Y aquí está la matriz de cuantificación habitual:
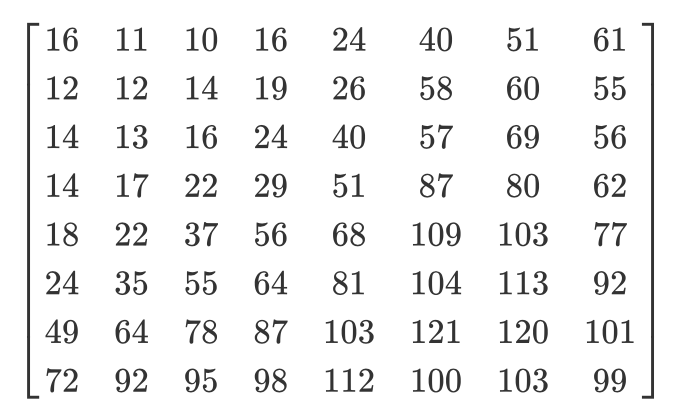
La matriz cuantificada se verá así:

Aunque el ser humano no puede ver la información de alta frecuencia, si elimina demasiados datos de los bloques de 8x8 píxeles, la imagen se verá demasiado tosca. En una matriz cuantificada de este tipo, el primer valor se denomina valor de CC y todos los demás se denominan valores de CA. Si tomamos los valores DC de todas las matrices cuantificadas y generamos una nueva imagen, obtendríamos una vista previa con una resolución 8 veces más pequeña que la imagen original.
También quiero señalar que, dado que utilizamos la cuantificación, debemos asegurarnos de que los colores estén dentro del rango de [0,255]. Si salen volando, tendrá que llevarlos manualmente a este rango.
Zigzag
Después de la cuantificación, el algoritmo JPEG utiliza un escaneo en zigzag para convertir la matriz a una forma unidimensional:
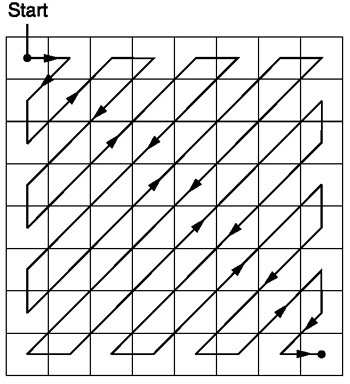
Fuente .
Tengamos tal matriz cuantificada:
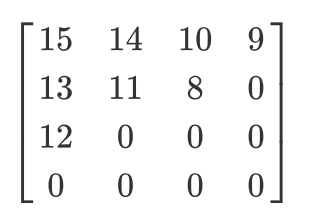
Entonces, el resultado del escaneo en zigzag será el siguiente:
[15 14 13 12 11 10 9 8 0 ... 0]
Se prefiere esta codificación porque después de la cuantificación, la mayor parte de la información de baja frecuencia (la más importante) se ubicará al comienzo de la matriz, y la exploración en zigzag almacena estos datos al comienzo de la matriz unidimensional. Esto es útil para el siguiente paso, la compresión.
Codificación de longitud de ejecución y codificación delta
La codificación de longitud de ejecución se utiliza para comprimir datos repetitivos. Después del escaneo en zigzag, vemos que en su mayoría hay ceros al final de la matriz. La codificación de longitud nos permite aprovechar este espacio desperdiciado y usar menos bytes para representar todos esos ceros. Digamos que tenemos los siguientes datos:
10 10 10 10 10 10 10
Después de codificar las longitudes de la serie, obtenemos esto:
7 10
Hemos comprimido 7 bytes en 2 bytes.
La codificación delta se utiliza para representar un byte en relación con el byte anterior. Será más fácil de explicar con un ejemplo. Tengamos los siguientes datos:
10 11 12 13 10 9
Mediante la codificación delta, se pueden representar de la siguiente manera:
10 1 2 3 0 -1
En JPEG, cada valor DC de la matriz DCT está codificado en delta en relación con el valor DC anterior. Esto significa que al cambiar el primer coeficiente DCT de la imagen, destruirá toda la imagen. Pero si cambia el primer valor de la última matriz DCT, solo afectará a un fragmento muy pequeño de la imagen.
Este enfoque es útil porque el primer valor de CC de la imagen suele ser el que más varía, y utilizamos la codificación delta para acercar los valores de CC restantes a 0, lo que mejora la compresión con la codificación de Huffman.
Codificación de Huffman
Es un método de compresión sin pérdidas. Huffman se preguntó una vez: "¿Cuál es la menor cantidad de bits que puedo usar para almacenar texto libre?" Como resultado, se creó un formato de codificación. Digamos que tenemos texto:
a b c d e
Normalmente, cada carácter ocupa un byte de espacio:
a: 01100001
b: 01100010
c: 01100011
d: 01100100
e: 01100101
Este es el principio de la codificación ASCII binaria. ¿Y si cambiamos el mapeo?
# Mapping
000: 01100001
001: 01100010
010: 01100011
100: 01100100
011: 01100101
Ahora necesitamos muchos menos bits para almacenar el mismo texto:
a: 000
b: 001
c: 010
d: 100
e: 011
Eso está muy bien, pero ¿y si necesitamos ahorrar aún más espacio? Por ejemplo, así:
# Mapping
0: 01100001
1: 01100010
00: 01100011
01: 01100100
10: 01100101
a: 0
b: 1
c: 00
d: 01
e: 10
La codificación de Huffman permite tal coincidencia de longitud variable. Se toman los datos de entrada, los caracteres más comunes se combinan con una combinación más pequeña de bits y los caracteres menos frecuentes, con combinaciones más grandes. Y luego las asignaciones resultantes se recopilan en un árbol binario. En JPEG, almacenamos información DCT mediante codificación Huffman. ¿Recuerda que mencioné que los valores DC de codificación delta facilitan la codificación de Huffman? Espero que ahora entiendas por qué. Después de la codificación delta, necesitamos hacer coincidir menos "caracteres" y el tamaño del árbol se reduce.
Tom Scott tiene un gran video que explica cómo funciona el algoritmo de Huffman. Eche un vistazo antes de seguir leyendo.
Un archivo JPEG contiene hasta cuatro tablas de Huffman, que se almacenan en "Definir tabla de Huffman" (comienza con
0xffc4). Los coeficientes DCT se almacenan en dos tablas de Huffman diferentes: en una, valores DC de tablas en zigzag, en el otro, valores AC de tablas en zigzag. Esto significa que al codificar, debemos combinar los valores de CC y CA de las dos matrices. La información DCT para los canales de luminancia y cromaticidad se almacena por separado, por lo que tenemos dos conjuntos de información de CC y dos conjuntos de información de CA, un total de 4 tablas de Huffman.
Si la imagen está en escala de grises, entonces solo tenemos dos tablas de Huffman (una para DC y otra para AC), porque no necesitamos color. Como puede haber descubierto, dos imágenes diferentes pueden tener tablas de Huffman muy diferentes, por lo que es importante almacenarlas dentro de cada JPEG.
Ahora conocemos el contenido principal de las imágenes JPEG. Pasemos a la decodificación.
Decodificación JPEG
La decodificación se puede dividir en etapas:
- Extracción de tablas Huffman y decodificación de bits.
- Extracción de coeficientes DCT mediante la reversión de codificación delta y de longitud de ejecución.
- Uso de coeficientes DCT para combinar ondas cosenoides y reconstruir valores de píxeles para cada bloque de 8x8.
- Convierta YCbCr a RGB para cada píxel.
- Muestra la imagen RGB resultante.
El estándar JPEG admite cuatro formatos de compresión:
- Base
- Serie extendida
- Progresivo
- Sin pérdida
Trabajaremos con compresión básica. Contiene una serie de bloques de 8x8, uno tras otro. En otros formatos, la plantilla de datos es ligeramente diferente. Para que quede claro, he coloreado en diferentes segmentos del contenido hexadecimal de nuestra imagen:
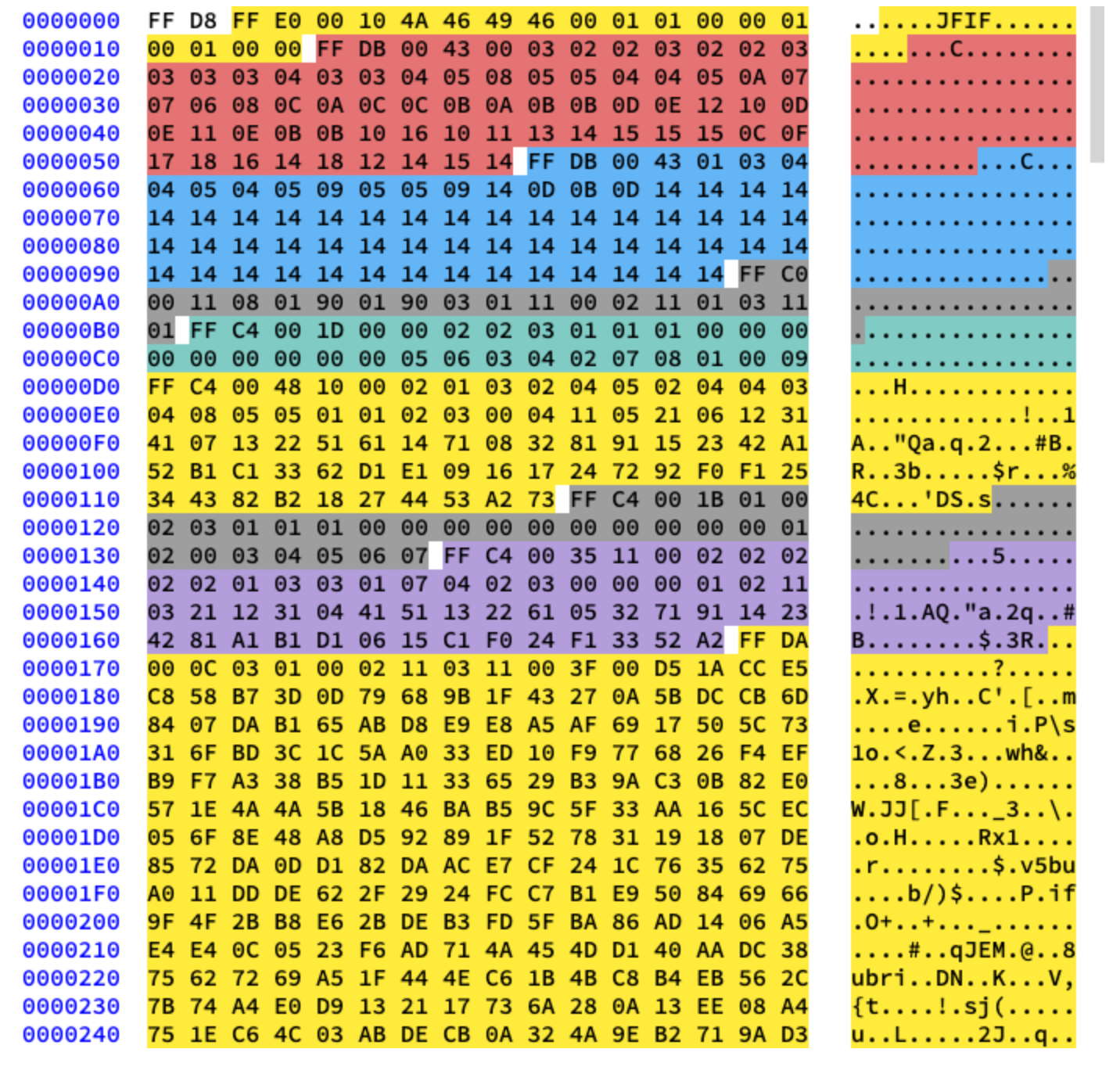
Extracción de tablas de Huffman
Ya sabemos que JPEG contiene cuatro tablas de Huffman. Esta es la última codificación, así que comenzaremos a decodificar con ella. Cada sección con la tabla contiene información:
| Campo | El tamaño | Descripción |
|---|---|---|
| ID de marcador | 2 bytes | 0xff y 0xc4 identifican DHT |
| Longitud | 2 bytes | Longitud de la mesa |
| Información de la tabla de Huffman | 1 byte | bits 0 ... 3: número de tablas (0 ... 3, en caso contrario error) bit 4: tipo de tabla, 0 = tabla de CC, 1 = tablas de CA bits 5 ... 7: no utilizado, debe ser 0 |
| Caracteres | 16 bytes | El número de caracteres con códigos de longitud 1 ... 16, suma (n) de estos bytes es el número total de códigos que deben ser <= 256 |
| Simbolos | n bytes | La tabla contiene caracteres en orden de longitud de código creciente (n = número total de códigos). |
Digamos que tenemos una tabla de Huffman como esta ( fuente ):
| Símbolo | Código Huffman | Longitud del código |
|---|---|---|
| un | 00 | 2 |
| segundo | 010 | 3 |
| C | 011 | 3 |
| re | 100 | 3 |
| mi | 101 | 3 |
| F | 110 | 3 |
| gramo | 1110 | 4 |
| h | 11110 | cinco |
| yo | 111110 | 6 |
| j | 1111110 | 7 |
| k | 11111110 | 8 |
| l | 111111110 | nueve |
Se almacenará en un archivo JFIF como este (en formato binario. Estoy usando ASCII solo para mayor claridad):
0 1 5 1 1 1 1 1 1 0 0 0 0 0 0 0 a b c d e f g h i j k l
0 significa que no tenemos un código Huffman de longitud 1. Un 1 significa que tenemos un código Huffman de longitud 2, y así sucesivamente. En la sección DHT, inmediatamente después de la clase y el ID, los datos siempre tienen una longitud de 16 bytes. Escribamos el código para extraer longitudes y elementos de DHT.
class JPEG:
# ...
def decodeHuffman(self, data):
offset = 0
header, = unpack("B",data[offset:offset+1])
offset += 1
# Extract the 16 bytes containing length data
lengths = unpack("BBBBBBBBBBBBBBBB", data[offset:offset+16])
offset += 16
# Extract the elements after the initial 16 bytes
elements = []
for i in lengths:
elements += (unpack("B"*i, data[offset:offset+i]))
offset += i
print("Header: ",header)
print("lengths: ", lengths)
print("Elements: ", len(elements))
data = data[offset:]
def decode(self):
data = self.img_data
while(True):
# ---
else:
len_chunk, = unpack(">H", data[2:4])
len_chunk += 2
chunk = data[4:len_chunk]
if marker == 0xffc4:
self.decodeHuffman(chunk)
data = data[len_chunk:]
if len(data)==0:
break
Después de ejecutar el código, obtenemos esto:
Start of Image
Application Default Header
Quantization Table
Quantization Table
Start of Frame
Huffman Table
Header: 0
lengths: (0, 2, 2, 3, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0)
Elements: 10
Huffman Table
Header: 16
lengths: (0, 2, 1, 3, 2, 4, 5, 2, 4, 4, 3, 4, 8, 5, 5, 1)
Elements: 53
Huffman Table
Header: 1
lengths: (0, 2, 3, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0)
Elements: 8
Huffman Table
Header: 17
lengths: (0, 2, 2, 2, 2, 2, 1, 3, 3, 1, 7, 4, 2, 3, 0, 0)
Elements: 34
Start of Scan
End of Image
¡Excelente! Disponemos de longitudes y elementos. Ahora necesita crear su propia clase de tabla Huffman para reconstruir un árbol binario a partir de las longitudes y elementos obtenidos. Copiaré el código de aquí :
class HuffmanTable:
def __init__(self):
self.root=[]
self.elements = []
def BitsFromLengths(self, root, element, pos):
if isinstance(root,list):
if pos==0:
if len(root)<2:
root.append(element)
return True
return False
for i in [0,1]:
if len(root) == i:
root.append([])
if self.BitsFromLengths(root[i], element, pos-1) == True:
return True
return False
def GetHuffmanBits(self, lengths, elements):
self.elements = elements
ii = 0
for i in range(len(lengths)):
for j in range(lengths[i]):
self.BitsFromLengths(self.root, elements[ii], i)
ii+=1
def Find(self,st):
r = self.root
while isinstance(r, list):
r=r[st.GetBit()]
return r
def GetCode(self, st):
while(True):
res = self.Find(st)
if res == 0:
return 0
elif ( res != -1):
return res
class JPEG:
# -----
def decodeHuffman(self, data):
# ----
hf = HuffmanTable()
hf.GetHuffmanBits(lengths, elements)
data = data[offset:]
GetHuffmanBitsToma la longitud y los elementos a través de los elementos y los coloca en una lista root. Es un árbol binario y contiene listas anidadas. Puede leer en Internet cómo funciona el árbol de Huffman y cómo crear dicha estructura de datos en Python. Para nuestro primer DHT (de la imagen al principio del artículo) tenemos los siguientes datos, longitudes y elementos:
Hex Data: 00 02 02 03 01 01 01 00 00 00 00 00 00 00 00 00
Lengths: (0, 2, 2, 3, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0)
Elements: [5, 6, 3, 4, 2, 7, 8, 1, 0, 9]
Después de la llamada, la
GetHuffmanBitslista rootcontendrá los siguientes datos:
[[5, 6], [[3, 4], [[2, 7], [8, [1, [0, [9]]]]]]]
HuffmanTabletambién contiene un método GetCodeque recorre el árbol y usa una tabla de Huffman para devolver los bits decodificados. El método recibe un flujo de bits como entrada, solo una representación binaria de los datos. Por ejemplo, el flujo de bits para abcserá 011000010110001001100011. Primero, convertimos cada carácter a su código ASCII, que convertimos a binario. Creemos una clase que nos ayude a convertir una cadena en bits y luego contemos los bits uno por uno:
class Stream:
def __init__(self, data):
self.data= data
self.pos = 0
def GetBit(self):
b = self.data[self.pos >> 3]
s = 7-(self.pos & 0x7)
self.pos+=1
return (b >> s) & 1
def GetBitN(self, l):
val = 0
for i in range(l):
val = val*2 + self.GetBit()
return val
Al inicializar, le damos a la clase datos binarios y luego los leemos usando
GetBity GetBitN.
Decodificación de la tabla de cuantificación
La sección Definir tabla de cuantificación contiene los siguientes datos:
| Campo | El tamaño | Descripción |
|---|---|---|
| ID de marcador | 2 bytes | 0xff y 0xdb identifican la sección DQT |
| Longitud | 2 bytes | Longitud de la tabla de cuantificación |
| Información de cuantificación | 1 byte | bits 0 ... 3: número de tablas de cuantificación (0 ... 3, en caso contrario error) bits 4 ... 7: precisión de la tabla de cuantificación, 0 = 8 bits, en caso contrario 16 bits |
| Bytes | n bytes | Valores de la tabla de cuantificación, n = 64 * (precisión + 1) |
Según el estándar JPEG, la imagen JPEG predeterminada tiene dos tablas de cuantificación: para luma y croma. Empiezan con un marcador
0xffdb. El resultado de nuestro código ya contiene dos de esos marcadores. Agreguemos la capacidad de decodificar tablas de cuantificación:
def GetArray(type,l, length):
s = ""
for i in range(length):
s =s+type
return list(unpack(s,l[:length]))
class JPEG:
# ------
def __init__(self, image_file):
self.huffman_tables = {}
self.quant = {}
with open(image_file, 'rb') as f:
self.img_data = f.read()
def DefineQuantizationTables(self, data):
hdr, = unpack("B",data[0:1])
self.quant[hdr] = GetArray("B", data[1:1+64],64)
data = data[65:]
def decodeHuffman(self, data):
# ------
for i in lengths:
elements += (GetArray("B", data[off:off+i], i))
offset += i
# ------
def decode(self):
# ------
while(True):
# ----
else:
# -----
if marker == 0xffc4:
self.decodeHuffman(chunk)
elif marker == 0xffdb:
self.DefineQuantizationTables(chunk)
data = data[len_chunk:]
if len(data)==0:
break
Primero definimos un método
GetArray. Es solo una técnica conveniente para decodificar un número variable de bytes a partir de datos binarios. También reemplazamos parte del código en el método decodeHuffmanpara aprovechar la nueva función. Luego se definió el método DefineQuantizationTables: lee el título de la sección con tablas de cuantificación, y luego aplica los datos de cuantificación al diccionario usando el valor del encabezado como clave. este valor puede ser 0 para luminancia y 1 para cromaticidad. Cada sección con tablas de cuantificación en JFIF contiene 64 bytes de datos (para una matriz de cuantificación de 8x8).
Si generamos las matrices de cuantificación para nuestra imagen, obtenemos esto:
3 2 2 3 2 2 3 3
3 3 4 3 3 4 5 8
5 5 4 4 5 10 7 7
6 8 12 10 12 12 11 10
11 11 13 14 18 16 13 14
17 14 11 11 16 22 16 17
19 20 21 21 21 12 15 23
24 22 20 24 18 20 21 20
3 2 2 3 2 2 3 3
3 2 2 3 2 2 3 3
3 3 4 3 3 4 5 8
5 5 4 4 5 10 7 7
6 8 12 10 12 12 11 10
11 11 13 14 18 16 13 14
17 14 11 11 16 22 16 17
19 20 21 21 21 12 15 23
24 22 20 24 18 20 21 20
Decodificando el inicio del cuadro
La sección Inicio del cuadro contiene la siguiente información ( fuente ):
| Campo | El tamaño | Descripción |
|---|---|---|
| ID de marcador | 2 bytes | 0xff 0xc0 SOF |
| 2 | 8 + *3 | |
| 1 | , 8 (12 16 ). | |
| 2 | > 0 | |
| 2 | > 0 | |
| 1 | 1 = , 3 = YcbCr YIQ | |
| 3 | 3 . (1 ) (1 = Y, 2 = Cb, 3 = Cr, 4 = I, 5 = Q), (1 ) ( 0...3 , 4...7 ), (1 ). |
Aquí no nos interesa todo. Extraeremos el ancho y alto de la imagen, así como el número de tablas de cuantificación para cada componente. El ancho y el alto se utilizarán para comenzar a decodificar los escaneos reales de la imagen desde la sección Inicio del escaneo. Dado que trabajaremos principalmente con una imagen YCbCr, podemos asumir que habrá tres componentes, y sus tipos serán 1, 2 y 3, respectivamente. Escribamos el código para decodificar estos datos:
class JPEG:
def __init__(self, image_file):
self.huffman_tables = {}
self.quant = {}
self.quantMapping = []
with open(image_file, 'rb') as f:
self.img_data = f.read()
# ----
def BaselineDCT(self, data):
hdr, self.height, self.width, components = unpack(">BHHB",data[0:6])
print("size %ix%i" % (self.width, self.height))
for i in range(components):
id, samp, QtbId = unpack("BBB",data[6+i*3:9+i*3])
self.quantMapping.append(QtbId)
def decode(self):
# ----
while(True):
# -----
elif marker == 0xffdb:
self.DefineQuantizationTables(chunk)
elif marker == 0xffc0:
self.BaselineDCT(chunk)
data = data[len_chunk:]
if len(data)==0:
break
Agregamos un atributo de lista a la clase JPEG
quantMappingy definimos un método BaselineDCTque decodifica los datos requeridos de la sección SOF y coloca el número de tablas de cuantificación para cada componente en la lista quantMapping. Aprovecharemos esto cuando comencemos a leer la sección Inicio del análisis. Así es como luce nuestra foto quantMapping:
Quant mapping: [0, 1, 1]
Inicio de decodificación de escaneo
Esta es la "carne" de una imagen JPEG, contiene los datos de la propia imagen. Hemos llegado a la etapa más importante. Todo lo que decodificamos antes puede considerarse una tarjeta que nos ayuda a decodificar la imagen en sí. Esta sección contiene la imagen en sí (codificada). Leemos la sección y desciframos utilizando los datos ya decodificados.
Todos los marcadores comenzaron con
0xff. Este valor también puede ser parte de la imagen escaneada, pero si está presente en esta sección, siempre irá seguido de y 0x00. El codificador JPEG lo inserta automáticamente, esto se llama relleno de bytes. Por lo tanto, el decodificador debe eliminarlos 0x00. Comencemos con el método de decodificación SOS que contiene dicha función y eliminemos las existentes 0x00. En nuestra imagen en la sección con un escaneo no hay0xffpero sigue siendo una adición útil.
def RemoveFF00(data):
datapro = []
i = 0
while(True):
b,bnext = unpack("BB",data[i:i+2])
if (b == 0xff):
if (bnext != 0):
break
datapro.append(data[i])
i+=2
else:
datapro.append(data[i])
i+=1
return datapro,i
class JPEG:
# ----
def StartOfScan(self, data, hdrlen):
data,lenchunk = RemoveFF00(data[hdrlen:])
return lenchunk+hdrlen
def decode(self):
data = self.img_data
while(True):
marker, = unpack(">H", data[0:2])
print(marker_mapping.get(marker))
if marker == 0xffd8:
data = data[2:]
elif marker == 0xffd9:
return
else:
len_chunk, = unpack(">H", data[2:4])
len_chunk += 2
chunk = data[4:len_chunk]
if marker == 0xffc4:
self.decodeHuffman(chunk)
elif marker == 0xffdb:
self.DefineQuantizationTables(chunk)
elif marker == 0xffc0:
self.BaselineDCT(chunk)
elif marker == 0xffda:
len_chunk = self.StartOfScan(data, len_chunk)
data = data[len_chunk:]
if len(data)==0:
break
Anteriormente, buscábamos manualmente el final del archivo cuando encontrábamos un marcador
0xffda, pero ahora que tenemos una herramienta que nos permite ver sistemáticamente todo el archivo, moveremos la condición de búsqueda del marcador dentro del operador else. La función RemoveFF00simplemente se interrumpe cuando encuentra algo más en lugar de 0x00después 0xff. El bucle se rompe cuando la función encuentra 0xffd9, por lo que podemos buscar el final del archivo sin temor a sorpresas. Si ejecuta este código, no verá nada nuevo en la terminal.
Recuerde, JPEG divide la imagen en matrices de 8x8. Ahora necesitamos convertir los datos de la imagen escaneada en un flujo de bits y procesarlos en trozos de 8x8. Agreguemos el código a nuestra clase:
class JPEG:
# -----
def StartOfScan(self, data, hdrlen):
data,lenchunk = RemoveFF00(data[hdrlen:])
st = Stream(data)
oldlumdccoeff, oldCbdccoeff, oldCrdccoeff = 0, 0, 0
for y in range(self.height//8):
for x in range(self.width//8):
matL, oldlumdccoeff = self.BuildMatrix(st,0, self.quant[self.quantMapping[0]], oldlumdccoeff)
matCr, oldCrdccoeff = self.BuildMatrix(st,1, self.quant[self.quantMapping[1]], oldCrdccoeff)
matCb, oldCbdccoeff = self.BuildMatrix(st,1, self.quant[self.quantMapping[2]], oldCbdccoeff)
DrawMatrix(x, y, matL.base, matCb.base, matCr.base )
return lenchunk +hdrlen
Comencemos por convertir los datos en un flujo de bits. ¿Recuerda que la codificación delta se aplica al elemento DC de la matriz de cuantificación (su primer elemento) en relación con el elemento DC anterior? Por lo tanto, inicializamos
oldlumdccoeff, oldCbdccoeffy oldCrdccoeffcon valores cero, nos ayudarán a realizar un seguimiento del valor de los elementos DC anteriores, y se establecerá 0 por defecto cuando encontremos el primer elemento DC.
El bucle
forpuede parecer extraño. self.height//8nos dice cuántas veces podemos dividir la altura entre 8 8, y es lo mismo con el ancho y self.width//8.
BuildMatrixtomará una tabla de cuantificación y agregará parámetros, creará una matriz de transformada de coseno discreta inversa y nos dará las matrices Y, Cr y Cb. Y la función los DrawMatrixconvierte a RGB.
Primero, creemos una clase
IDCTy luego comience a completar el método BuildMatrix.
import math
class IDCT:
"""
An inverse Discrete Cosine Transformation Class
"""
def __init__(self):
self.base = [0] * 64
self.zigzag = [
[0, 1, 5, 6, 14, 15, 27, 28],
[2, 4, 7, 13, 16, 26, 29, 42],
[3, 8, 12, 17, 25, 30, 41, 43],
[9, 11, 18, 24, 31, 40, 44, 53],
[10, 19, 23, 32, 39, 45, 52, 54],
[20, 22, 33, 38, 46, 51, 55, 60],
[21, 34, 37, 47, 50, 56, 59, 61],
[35, 36, 48, 49, 57, 58, 62, 63],
]
self.idct_precision = 8
self.idct_table = [
[
(self.NormCoeff(u) * math.cos(((2.0 * x + 1.0) * u * math.pi) / 16.0))
for x in range(self.idct_precision)
]
for u in range(self.idct_precision)
]
def NormCoeff(self, n):
if n == 0:
return 1.0 / math.sqrt(2.0)
else:
return 1.0
def rearrange_using_zigzag(self):
for x in range(8):
for y in range(8):
self.zigzag[x][y] = self.base[self.zigzag[x][y]]
return self.zigzag
def perform_IDCT(self):
out = [list(range(8)) for i in range(8)]
for x in range(8):
for y in range(8):
local_sum = 0
for u in range(self.idct_precision):
for v in range(self.idct_precision):
local_sum += (
self.zigzag[v][u]
* self.idct_table[u][x]
* self.idct_table[v][y]
)
out[y][x] = local_sum // 4
self.base = out
Analicemos la clase
IDCT. Cuando extraemos la MCU, se almacenará en un atributo base. Luego transformamos la matriz de MCU retrocediendo el escaneo en zigzag usando el método rearrange_using_zigzag. Finalmente, revertiremos la transformada de coseno discreta llamando al método perform_IDCT.
Como recordará, la tabla de CC está fija. No consideraremos cómo funciona DCT, esto está más relacionado con las matemáticas que con la programación. Podemos almacenar esta tabla como una variable global y consultar pares de valores
x,y. Decidí poner la tabla y su cálculo en una clase IDCTpara que el texto fuera legible. Cada elemento de la matriz MCU transformada se multiplica por un valor idc_variabley obtenemos los valores Y, Cr y Cb.
Esto quedará más claro cuando agreguemos el método
BuildMatrix.
Si modifica la tabla en zigzag para que se vea así:
[[ 0, 1, 5, 6, 14, 15, 27, 28],
[ 2, 4, 7, 13, 16, 26, 29, 42],
[ 3, 8, 12, 17, 25, 30, 41, 43],
[20, 22, 33, 38, 46, 51, 55, 60],
[21, 34, 37, 47, 50, 56, 59, 61],
[35, 36, 48, 49, 57, 58, 62, 63],
[ 9, 11, 18, 24, 31, 40, 44, 53],
[10, 19, 23, 32, 39, 45, 52, 54]]
obtienes este resultado (ten en cuenta los pequeños artefactos):

Y si tienes el coraje, puedes modificar aún más la mesa en zigzag:
[[12, 19, 26, 33, 40, 48, 41, 34,],
[27, 20, 13, 6, 7, 14, 21, 28,],
[ 0, 1, 8, 16, 9, 2, 3, 10,],
[17, 24, 32, 25, 18, 11, 4, 5,],
[35, 42, 49, 56, 57, 50, 43, 36,],
[29, 22, 15, 23, 30, 37, 44, 51,],
[58, 59, 52, 45, 38, 31, 39, 46,],
[53, 60, 61, 54, 47, 55, 62, 63]]
Entonces el resultado será así:

Completemos nuestro método
BuildMatrix:
def DecodeNumber(code, bits):
l = 2**(code-1)
if bits>=l:
return bits
else:
return bits-(2*l-1)
class JPEG:
# -----
def BuildMatrix(self, st, idx, quant, olddccoeff):
i = IDCT()
code = self.huffman_tables[0 + idx].GetCode(st)
bits = st.GetBitN(code)
dccoeff = DecodeNumber(code, bits) + olddccoeff
i.base[0] = (dccoeff) * quant[0]
l = 1
while l < 64:
code = self.huffman_tables[16 + idx].GetCode(st)
if code == 0:
break
# The first part of the AC quantization table
# is the number of leading zeros
if code > 15:
l += code >> 4
code = code & 0x0F
bits = st.GetBitN(code)
if l < 64:
coeff = DecodeNumber(code, bits)
i.base[l] = coeff * quant[l]
l += 1
i.rearrange_using_zigzag()
i.perform_IDCT()
return i, dccoeff
Comenzamos creando una clase invertida de transformada de coseno discreta (
IDCT()). Luego leemos los datos en el flujo de bits y los decodificamos usando una tabla de Huffman.
self.huffman_tables[0]y self.huffman_tables[1]consulte las tablas de CC para luma y croma, respectivamente, y self.huffman_tables[16]y self.huffman_tables[17]consulte las tablas de CA para luma y croma, respectivamente.
Después de decodificar el flujo de bits, usamos una función para
DecodeNumber extraer el nuevo coeficiente de CC codificado en delta y agregarlo olddccoefficientpara obtener el coeficiente de CC decodificado en delta .
Luego repetimos el mismo procedimiento de decodificación con los valores de CA en la matriz de cuantificación. Significado del código
0indica que hemos llegado al marcador de Fin de Bloque (EOB) y debemos detenernos. Además, la primera parte de la tabla de cuantificación de CA nos dice cuántos ceros a la izquierda tenemos. Ahora recordemos cómo codificar las longitudes de la serie. Invirtamos este proceso y saltemos todos esos bits. IDCTSe les asignan ceros explícitamente en la clase .
Después de decodificar los valores de CC y CA para la MCU, convertimos la MCU e invertimos el escaneo en zigzag llamando
rearrange_using_zigzag. Y luego invertimos el DCT y lo aplicamos al MCU decodificado.
El método
BuildMatrixdevolverá la matriz DCT invertida y el valor del coeficiente DC. Recuerde que esta será una matriz para solo una unidad de codificación mínima de 8x8. Hagamos esto para todas las demás MCU de nuestro archivo.
Visualización de una imagen en la pantalla
Ahora hagamos que nuestro código en el método
StartOfScancree un Tkinter Canvas y dibujemos cada MCU después de la decodificación.
def Clamp(col):
col = 255 if col>255 else col
col = 0 if col<0 else col
return int(col)
def ColorConversion(Y, Cr, Cb):
R = Cr*(2-2*.299) + Y
B = Cb*(2-2*.114) + Y
G = (Y - .114*B - .299*R)/.587
return (Clamp(R+128),Clamp(G+128),Clamp(B+128) )
def DrawMatrix(x, y, matL, matCb, matCr):
for yy in range(8):
for xx in range(8):
c = "#%02x%02x%02x" % ColorConversion(
matL[yy][xx], matCb[yy][xx], matCr[yy][xx]
)
x1, y1 = (x * 8 + xx) * 2, (y * 8 + yy) * 2
x2, y2 = (x * 8 + (xx + 1)) * 2, (y * 8 + (yy + 1)) * 2
w.create_rectangle(x1, y1, x2, y2, fill=c, outline=c)
class JPEG:
# -----
def StartOfScan(self, data, hdrlen):
data,lenchunk = RemoveFF00(data[hdrlen:])
st = Stream(data)
oldlumdccoeff, oldCbdccoeff, oldCrdccoeff = 0, 0, 0
for y in range(self.height//8):
for x in range(self.width//8):
matL, oldlumdccoeff = self.BuildMatrix(st,0, self.quant[self.quantMapping[0]], oldlumdccoeff)
matCr, oldCrdccoeff = self.BuildMatrix(st,1, self.quant[self.quantMapping[1]], oldCrdccoeff)
matCb, oldCbdccoeff = self.BuildMatrix(st,1, self.quant[self.quantMapping[2]], oldCbdccoeff)
DrawMatrix(x, y, matL.base, matCb.base, matCr.base )
return lenchunk+hdrlen
if __name__ == "__main__":
from tkinter import *
master = Tk()
w = Canvas(master, width=1600, height=600)
w.pack()
img = JPEG('profile.jpg')
img.decode()
mainloop()
Comencemos con las funciones
ColorConversiony Clamp. ColorConversiontoma los valores Y, Cr y Cb, los convierte en componentes RGB mediante la fórmula y luego genera los valores RGB agregados. ¿Por qué agregar 128 a ellos? Recuerde, antes del algoritmo JPEG, DCT se aplica a la MCU y resta 128 de los valores de color. Si los colores estaban originalmente en el rango [0,255], JPEG los pondrá en el rango [-128, + 128]. Necesitamos revertir este efecto al decodificar, por lo que agregamos 128 a RGB. En cuanto a Clamp, al desempaquetar, los valores resultantes pueden salir del rango [0.255], por lo que los mantenemos en este rango [0.255].
En el método
DrawMatrixrecorremos cada matriz decodificada de 8x8 para Y, Cr y Cb, y convertimos cada elemento de la matriz a valores RGB. Después de transformar, dibujamos píxeles en Tkinter canvasusando el método create_rectangle. Puedes encontrar todo el código en GitHub . Si lo ejecuta, mi cara aparecerá en la pantalla.
Conclusión
Quién hubiera pensado que para mostrar mi cara tendrías que escribir una explicación de más de 6.000 palabras. ¡Es asombroso lo inteligentes que fueron los autores de algunos de los algoritmos! Espero que hayas disfrutado del artículo. Aprendí mucho escribiendo este decodificador. No pensé que hubiera tantas matemáticas involucradas en la codificación de una imagen JPEG simple. La próxima vez puede intentar escribir un decodificador para PNG (u otro formato).
Materiales adicionales
Si te interesan los detalles, lee los materiales que utilicé para escribir el artículo, así como algún trabajo adicional:
- Guía ilustrada para desentrañar JPEG
- Un artículo muy detallado sobre la codificación de Huffman en JPEG
- Escribir una biblioteca JPEG simple en C ++
- Documentación para estructura en Python 3
- Cómo FB aprovechó el conocimiento de JPEG
- Diseño y formato JPEG
- Interesante presentación del Departamento de Defensa sobre análisis forense de JPEG