Comparar diferentes métodos de fusionar dos listas ordenadas

Supongamos que tenemos dos listas (de enteros para simplificar), cada una de las cuales está ordenada. Queremos combinarlos en una lista, que también debe ordenarse. Esta tarea probablemente sea familiar para todos; se usa, por ejemplo, en ordenación por combinación.

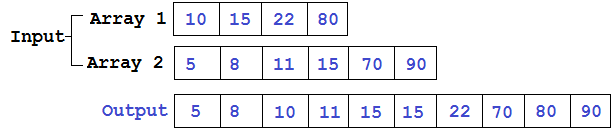
Hay muchas formas de implementación (especialmente en Python). Echemos un vistazo a algunos de ellos y comparemos el tiempo transcurrido para diferentes entradas.

La idea principal del algoritmo es que al colocar una etiqueta al comienzo de cada lista, compararemos los elementos marcados, tomaremos el más pequeño y moveremos la etiqueta en su lista al siguiente número. Cuando termina una de las listas, debe agregar el resto de la segunda al final.

Los datos de entrada no cambian

Que haya dos listas list1y list2.

Vamos a empezar con el algoritmo más simple: que marquemos las etiquetas para iy jy tomar la más pequeña list1[i], list2[j]y aumentar su etiqueta por uno hasta que uno de los sellos va más allá de los límites de la lista.

, . , .

:

def simple_merge(list1, list2):
    i, j = 0, 0
    res = []
    while i < len(list1) and j < len(list2):
        if list1[i] < list2[j]:
            res.append(list1[i])
            i += 1
        else:
            res.append(list2[j])
            j += 1
    res += list1[i:]
    res += list2[j:] 
    #   list1[i:]  list2[j:]   ,     
    return res

, . . .

, . , , , , .

def iter_merge(list1, list2):
    result, it1, it2 = [], iter(list1), iter(list2)
    el1 = next(it1, None)
    el2 = next(it2, None)
    while el1 is not None or el2 is not None:
        if el1 is None or (el2 is not None and el2 < el1):
            result.append(el2)
            el2 = next(it2, None)
        else:
            result.append(el1)
            el1 = next(it1, None)
    return result

(result.append()) , . , , .

def gen_merge_inner(it1, it2):
    el1 = next(it1, None)
    el2 = next(it2, None)
    while el1 is not None or el2 is not None:
        if el1 is None or (el2 is not None and el2 < el1):
            yield el2
            el2 = next(it2, None)
        else:
            yield el1
            el1 = next(it1, None)

def gen_merge(list1, list2):
    return list(gen_merge_inner(iter(list1), iter(list2))) #    

python .

• merge heapq. , , , : , , .

  
  
  

  :

  
  
  

  from heapq import merge
  
  def heapq_merge(list1, list2):
  return list(merge(list1, list2)) #   

  
  
  

• Counter collections. Counter , , , , (, ).

  
  
  

  gen_merge_inner Counter(list1) Counter(list2):

  
  
  

  def counter_merge(list1, list2):
  return list(gen_merge_inner(Counter(list1).elements(), Counter(list2).elements()))

  
  
  

• , , . .

  
  
  

  def sort_merge(list1, list2):
  return sorted(list1 + list2)

  
  
  

, ( ). . pop(0) , .

def pop_merge(list1, list2):
    result = []
    while list1 and list2:
        result.append((list1 if list1[0] < list2[0] else list2).pop(0))
    return result + list1 + list2

4 , . , , . , . , , .

def reverse_pop_merge(list1, list2):
    result = []
    while list1 and list2:
        result.append((list1 if list1[-1] > list2[-1] else list2).pop(-1))
    return (result + list1[-1::-1] + list2[-1::-1])[-1::-1]

.

, :

• simple_merge
• iter_merge
• gen_merge
• heapq_merge
• counter_merge
• sort_merge
• pop_merge
• reverse_pop_merge

timeit. .

: , , , , . .

, $$$1$ $$$10^5$, $$$1$ $$$10^6$.

pop reverse_pop:

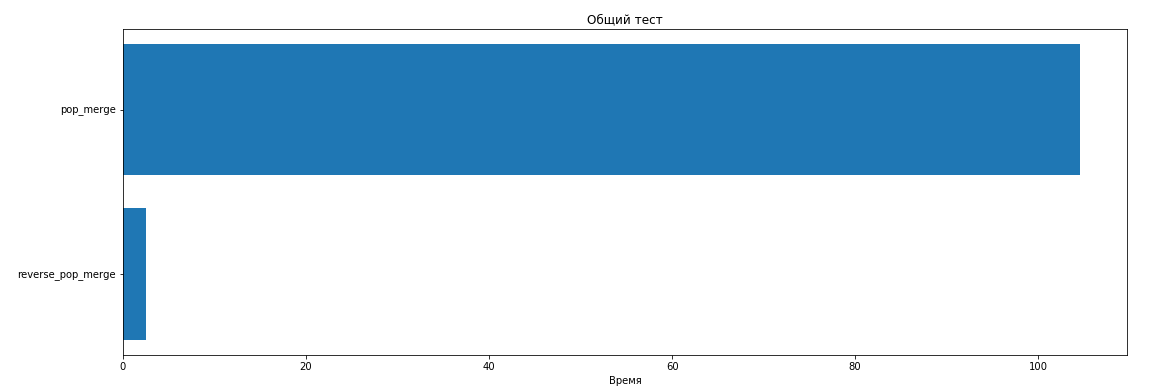
pop_merge , .

pop_merge, :

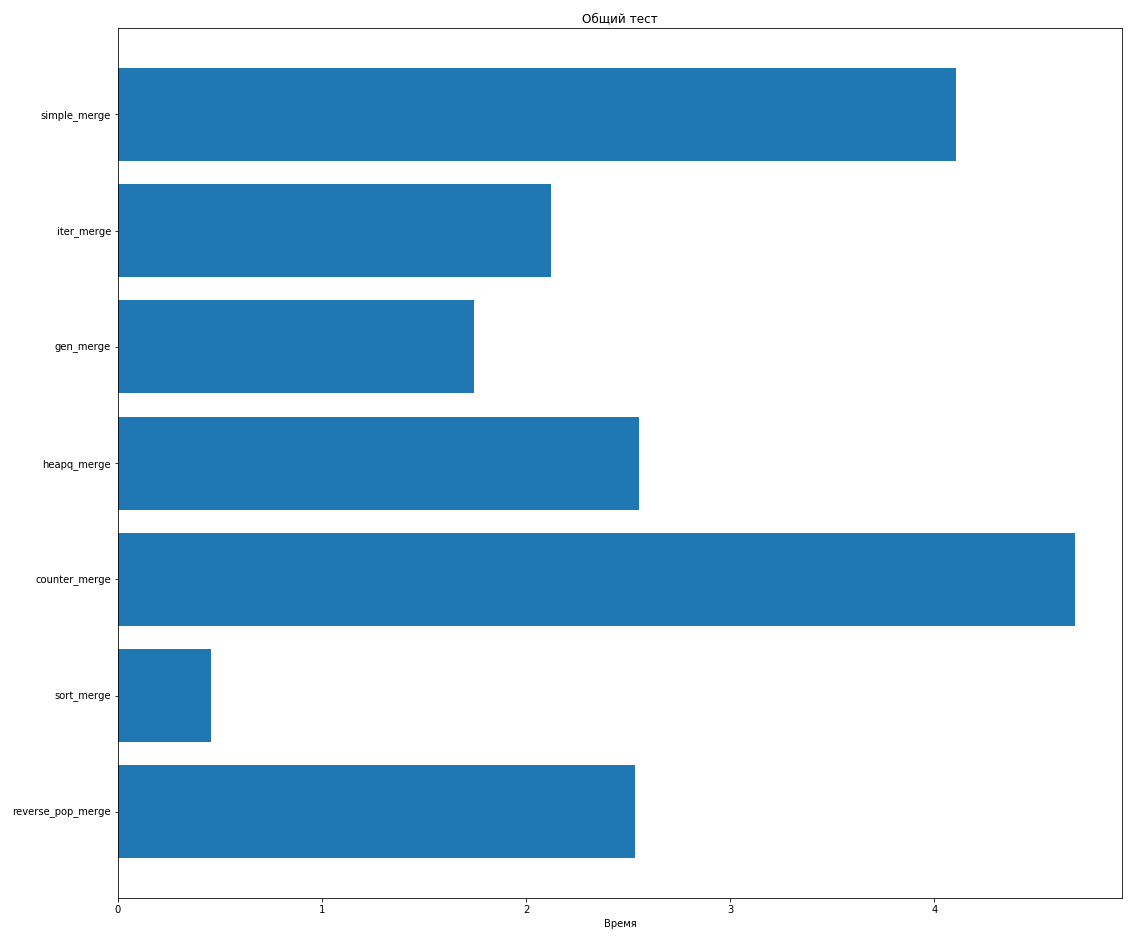
reverse_pop_merge heapq_merge.

, , , .

,

$$$[50x, 50(x+1))$, $$$x$ , $$$1$. $$$50$.

pop_merge heapq_merge, .

, ,

$$$x$, $$$10^4 + 100x$.

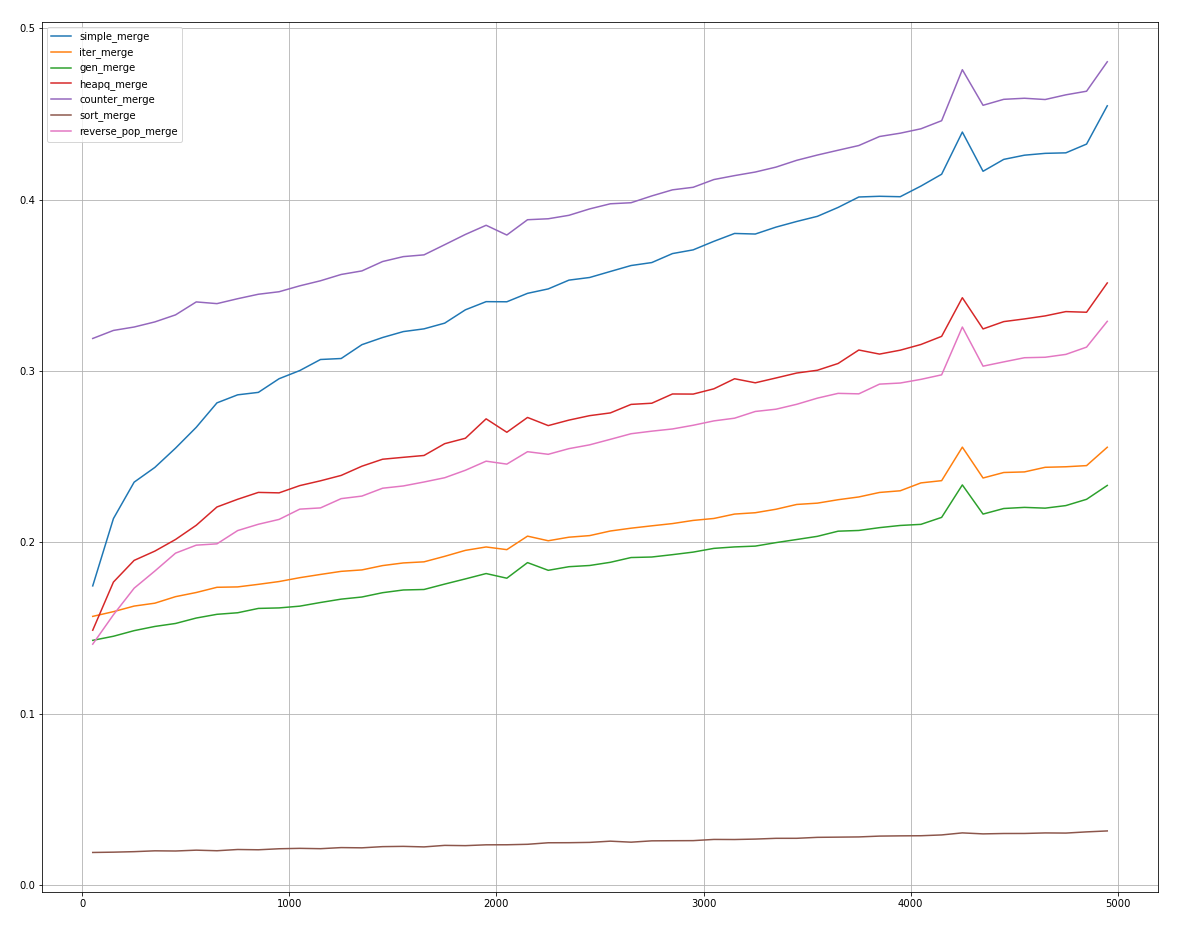
( ) reverse_pop_merge , sort_merge, .

,

, $$$5$, $$$1$.

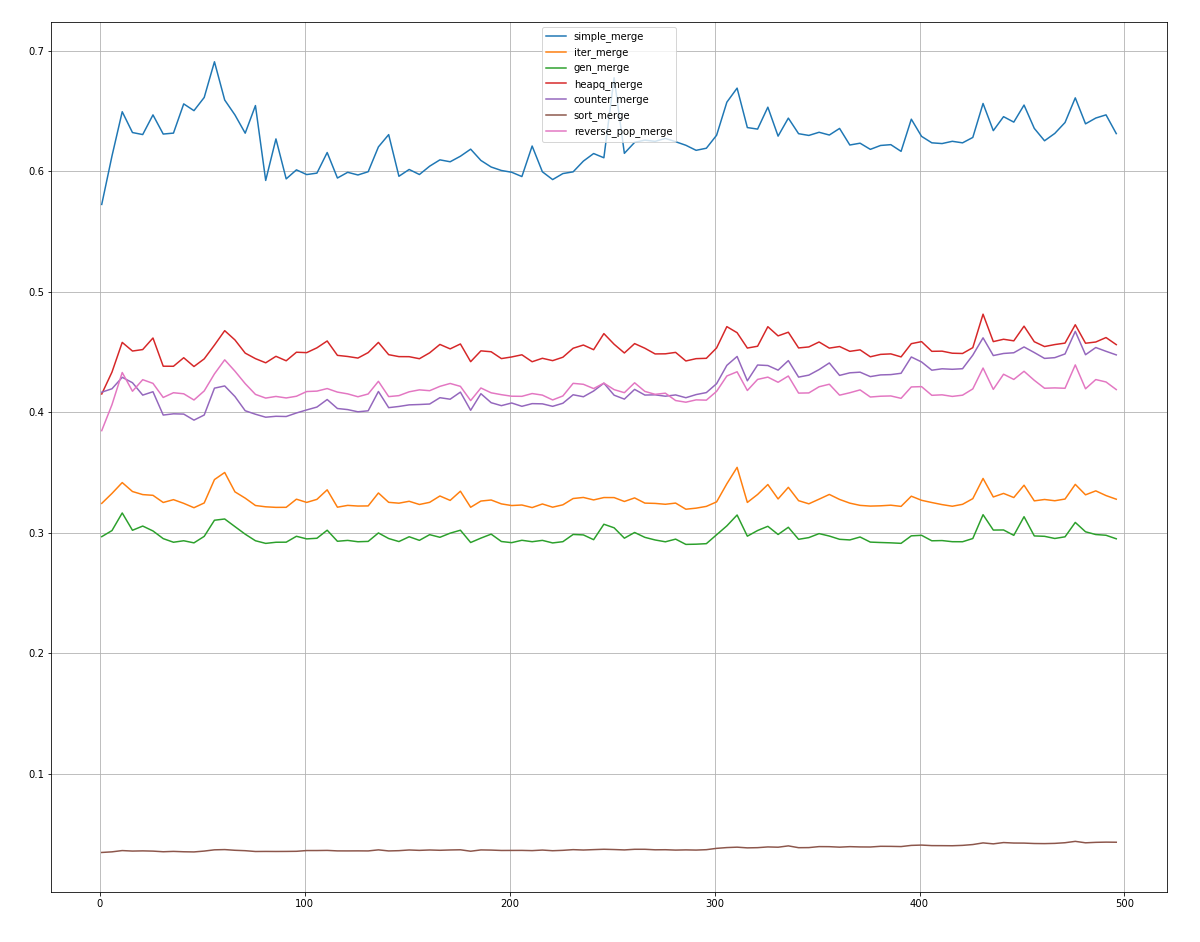
, counter_merge reverse_pop_merge heapq_merge, .

sort_merge! , .

En segundo lugar, en la inmensa mayoría de los casos, viene gen_mergeseguido de iter_merge.

El resto de métodos emplean incluso más tiempo, pero algunos, en algunos casos extremos, consiguen resultados de 2-3 lugares.

PD

El código, las pruebas y el cuaderno jupyter con gráficos se pueden encontrar en gitlab .

Quizás este análisis esté incompleto, me complacerá agregar sus opciones a la comparación, sugiero.