Entendemos y creamos
Las buenas noticias antes del artículo: no se requieren altas habilidades matemáticas para leer y (¡con suerte!) Comprensión.
Aviso legal: la parte de código de este artículo, como el anterior , es una traducción adaptada, complementada y probada. Estoy agradecido con el autor, porque esta es una de mis primeras experiencias en el código, después de lo cual inundé aún más. ¡Espero que mi adaptación funcione igual para ti!
¡Entonces vamos!
La estructura es así:
- ¿Qué es una cadena de Markov?
- Un ejemplo de cómo funciona la cadena
- Matriz de transición
- Modelo de cadena de Markov con Python: generación de texto basada en datos
¿Qué es una cadena de Markov?
La cadena de Markov es una herramienta de la teoría de procesos aleatorios, que consta de una secuencia de n números de estados. En este caso, las conexiones entre los nodos (valores) de la cadena se crean solo si los estados están estrictamente uno al lado del otro.
Teniendo en cuenta la palabra zhirnoshriftovoe única , derivar la propiedad de las cadenas de Markov:
La probabilidad de que un nuevo estado en la cadena depende sólo del estado actual y matemáticamente no toma en cuenta la experiencia de los estados pasados => cadena de Markov - una cadena sin memoria.
En otras palabras, un nuevo significado siempre baila del que lo sujeta directamente por el mango.
Un ejemplo de cómo funciona la cadena
Como el autor del artículo, del que se tomó prestada la implementación del código, tomemos una secuencia aleatoria de palabras.
Inicio - artificial - abrigo de piel - artificial - comida - artificial - pasta - artificial - abrigo de piel - artificial - fin
Imaginemos que este es en realidad un gran verso y nuestra tarea es copiar el estilo del autor. (Pero hacerlo, por supuesto, no es ético)
¿Cómo decidir?
La primera cosa obvia que quiero hacer es contar la frecuencia de las palabras (si hiciéramos esto con un texto en vivo, primero valdría la pena realizar la normalización, para llevar cada palabra a un lema (forma de diccionario)).
Inicio == 1
Artificial == 5
Abrigo de piel == 2
Pasta == 1
Comida == 1
Fin == 1
Teniendo en cuenta que tenemos una cadena de Markov, podemos trazar gráficamente la distribución de nuevas palabras en función de las anteriores:

Verbalmente:
- el estado del abrigo de piel, comida y pasta 100% conlleva el estado de artificial p = 1
- el estado "artificial" puede llevar a 4 condiciones con igual probabilidad, y la probabilidad de llegar al estado de un abrigo de piel artificial es mayor que a las otras tres
- el estado final no lleva a ninguna parte
- el estado "inicio" 100% implica el estado "artificial"
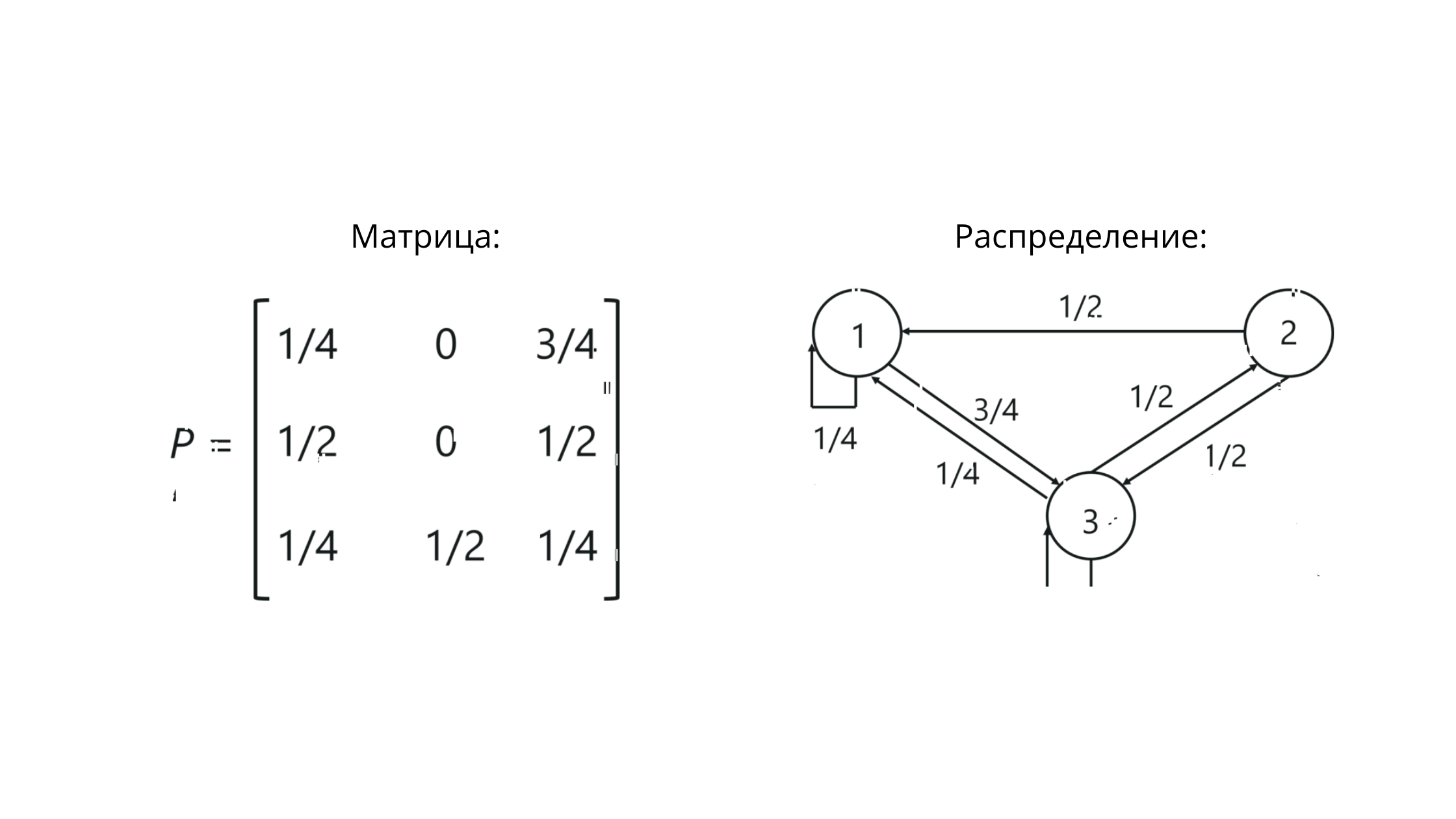
Parece genial y lógico, ¡pero la belleza visual no termina ahí! También podemos construir una matriz de transición, y sobre esta base podemos apelar a la siguiente justicia matemática:

Lo que en ruso significa “la suma de una serie de probabilidades para un cierto evento k, dependiendo de i == la suma de todos los valores de las probabilidades del evento k, dependiendo de la ocurrencia del estado i, donde el evento k == m + 1, y evento i == m (es decir, el evento k siempre difiere en uno de i) ”.
Pero primero, entendamos qué es una matriz.
Matriz de transición
Cuando se trabaja con cadenas de Markov, se trata de una matriz de transición estocástica: un conjunto de vectores, dentro de los cuales los valores reflejan los valores de las probabilidades entre gradaciones.
Sí, sí, parece que suena.
Pero no parece tan aterrador:

P es la notación de una matriz. Los valores en la intersección de columnas y filas aquí reflejan las probabilidades de transiciones entre estados.
Para nuestro ejemplo, se verá así:

Observe que la suma de los valores en la fila == 1. Esto significa que hemos construido todo correctamente, porque la suma de los valores en la fila de la matriz estocástica debe ser igual a uno.
Ejemplo desnudo sin abrigos y pastas de piel sintética: Un
ejemplo incluso desnudo es la matriz de identidad para:
- el caso en el que es imposible volver de A a B, y de B - volver a A [1]
- el caso en el que la transición de A a B hacia atrás es posible [2]

Respecto. Con la teoría terminada.
Usamos Python.
Un modelo basado en la cadena de Markov usando Python: generación de texto basado en datos
Paso 1
Importe el paquete relevante para el trabajo y obtenga los datos.
import numpy as np
data = open('/Users/sad__sabrina/Desktop/1.txt', encoding='utf8').read()
print(data)
, , , , ( « memorylessness »). , , , , , , ; .., , .
No se centre en la estructura del texto, pero preste atención a la codificación utf8. Esto es importante para leer los datos.
Paso 2
Divida los datos en palabras.
ind_words = data.split()
print(ind_words)
['\ufeff', '', '', '', '', ',', '', '', ',', '', '', '', '', '', '', '', ',', '', '', '', ',', '', '', '', '', '(', '', '', '«', 'memorylessness', '»).', '', ',', '', '', '', '', ',', '', '', '', '', '', '', '', ',', '', '', '', '', '', '', '', '', '', ',', '', '', '', '', '', '', '', ',', '', '', ',', '', '', '', ';', '..,', '', '', '', '', ',', '', '', '', '', '', '', '.']Paso 3
Creemos una función para vincular pares de palabras.
def make_pairs(ind_words):
for i in range(len(ind_words) - 1):
yield (ind_words[i], ind_words[i + 1])
pair = make_pairs(ind_words)El principal matiz de la función en el uso del operador yield (). Nos ayuda a cumplir con el criterio de encadenamiento de Markov, el criterio de almacenamiento sin memoria. Con rendimiento, nuestra función creará nuevos pares a medida que itera (repeticiones), en lugar de almacenar todo.
Puede surgir un malentendido aquí, porque una palabra puede convertirse en otras diferentes. Resolveremos esto creando un diccionario para nuestra función.
Paso 4
word_dict = {}
for word_1, word_2 in pair:
if word_1 in word_dict.keys():
word_dict[word_1].append(word_2)
else:
word_dict[word_1] = [word_2]Aquí:
- si ya tenemos una entrada sobre la primera palabra de un par en el diccionario, la función agrega el siguiente valor potencial a la lista.
- de lo contrario: se crea una nueva entrada.
Paso 5
Escojamos aleatoriamente la primera palabra y, para hacer que la palabra sea verdaderamente aleatoria, establezcamos la condición while usando el método de cadena islower (), que satisface True si la cadena contiene letras minúsculas, permitiendo la presencia de números o símbolos.
En este caso, estableceremos el número de palabras en 20.
first_word = np.random.choice(ind_words)
while first_word.islower():
chain = [first_word]
n_words = 20
first_word = np.random.choice(ind_words)
for i in range(n_words):
chain.append(np.random.choice(word_dict[chain[-1]]))Paso 6
¡Comencemos con lo aleatorio!
print(' '.join(chain))
; .., , , (La función join () es una función para trabajar con cadenas. Entre paréntesis, hemos especificado un separador para los valores en la línea (espacio).
Y el texto ... bueno, suena a máquina y casi lógico.
PD Como habrás notado, las cadenas de Markov son útiles en lingüística, pero su aplicación va más allá del procesamiento del lenguaje natural. Aquí y aquí puede familiarizarse con el uso de cadenas en otras tareas.
PPS Si mi código de práctica resultó incomprensible para usted, le adjunto el artículo original . Asegúrese de aplicar el código en la práctica: ¡la sensación cuando "se ejecutó y generó" se está cargando!
¡Estoy esperando sus opiniones y estaré encantado de tener comentarios constructivos sobre el artículo!