👨🏼‍⚖️ 👆 👶🏽 Construcción de la curva de descuento. Programa educativo para geek, parte 5 🦑 🗻 🐭

Aprendamos a construir una curva de descuento. Diré de inmediato: es muy importante tener datos de mercado actualizados. Si está buscando permutas de tasas de interés para el dólar, el euro o alguna otra moneda, no hay mucha información abierta en Internet. La mayoría de los datos están disponibles a través de terminales comerciales o de empresas especiales: proveedores de datos de mercado. Encontré datos sobre la corona danesa, sueca y noruega, así como datos sobre el euro y el dólar en el sitio web de un gran grupo bancario escandinavo.

A continuación, intentaremos construir una curva de descuento para la corona sueca.

Esta publicación es una versión adaptada de mi tercera conferencia en video " Construyendo la curva de descuento " como parte del curso Finmath para Fintech.

Entonces, nuestra curva de descuento para la corona serán las tarifas nocturnas para cada día. Lo primero que sabemos es la denominada tasa base , la tasa de los depósitos a corto (préstamos). Además, se conocen permutas que van desde un año hasta treinta años. Para ilustrar el método, trazaremos una curva de hasta diez años. Los valores actuales de los datos del mercado se pueden ver en esta imagen:

Para comenzar a trazar la curva, necesitamos hacer algunas suposiciones.

Supongamos, en aras de la simplicidad, que nuestros swaps son swaps flotantes fijos con una periodicidad de pagos cada seis meses. A continuación se muestra el diagrama para un intercambio de un año. Sabemos que al principio la tasa base es cero por ciento. Para calcular el precio de intercambio justo, necesitamos conocer el valor del factor de descuento de seis meses y el factor de descuento de 12 meses. ¿Qué tendremos como "pierna" flotante? Supongamos que así pagaremos el valor medio nocturno para cada uno de los rangos. Es decir, el valor del "tramo" flotante hasta seis meses: este será el valor medio durante la noche durante 180 días. El tramo flotante para el punto de 12 meses será el mismo, solo que aquí habrá una suma desde el día 181 al día 360.

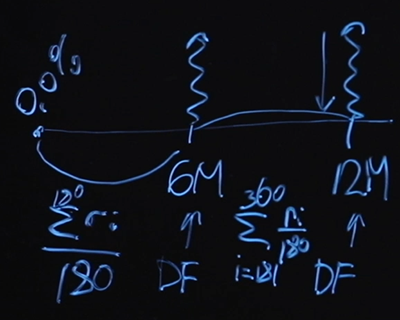
Este método de promediado es ampliamente conocido. Se llama swap de índice nocturno y se utiliza con mucha frecuencia en productos de mercado. El tramo flotante se define aquí como el promedio durante el período.

Conocemos la tasa base y el costo del swap. Obviamente, si escribimos la fórmula para un precio justo "de frente", entonces tendremos demasiadas incógnitas. No conocemos el factor de descuento durante 6 meses, el factor de descuento durante 12 meses, y no conocemos los valores de las tasas de interés excepto uno: el primero. Demasiadas incógnitas y una sola ecuación.

La siguiente hipótesis nos ayudará a resolver este problema. Conocemos la tasa de interés en el punto cero; esta es la tasa base. Supondremos que nuestras tasas de interés están cambiando linealmente. Designemos como X el valor de la tasa de interés en el punto de 12 meses.

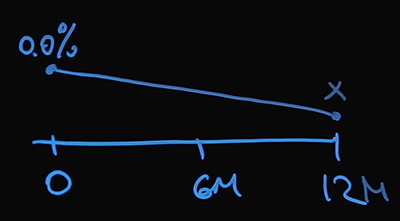
A los 6 meses será X / 2 (la media aritmética entre cero y X), y podemos encontrar el valor de la tasa de interés en cualquier día arbitrario. Y no hay nada difícil en calcular nuestro tipo de interés variable en los puntos 6 y 12 meses:

\begin{array}{rcl} L_{1} & = & \frac{X}{4} \end{array}

$\begin{eqnarray} L_1&=& \frac{X}{4} \end{eqnarray}$

\begin{array}{rcl} L_{1} & = & \frac{3 X}{4} \end{array}

$\begin{eqnarray} L_1&=& \frac{3X}{4} \end{eqnarray}$

Pasemos ahora a los factores de descuento. Usamos una curva de descuento basada en el tipo de cambio a un día. Por lo tanto, el factor de descuento en el punto seis meses es el producto de 180 factores de descuento en cada punto, y esto obviamente será algún tipo de función de X. El

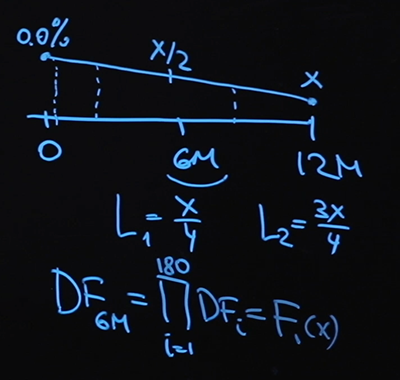
factor de descuento en el punto 12 meses se construye de la misma manera con la única diferencia que necesito más multiplicadores. Esto también será una función de X.

Entonces, los factores de descuento se expresan en términos de X, también están los valores primero y segundo de la tasa flotante. Pasemos a escribir la ecuación. Conocemos el valor del precio de intercambio, digamos que es igual a P. Recuerde la ecuación del precio justo. Necesitamos multiplicar P por el factor de descuento en el punto de doce meses y equipararlo a la siguiente suma:

Permítame recordarle que el factor de descuento para un día será determinado por la siguiente fórmula:

\begin{array}{rcl} D F_{i} & = & \frac{1}{(1 + \frac{r_{i}}{360})} \end{array}

$\begin{eqnarray} DF_i&=& \frac{1}{(1+\frac{r_i}{360})} \end{eqnarray}$

donde r _i es el valor de la tasa de interés. Utilizo el número 360 suponiendo que hay 360 días en un año (esta es una convención muy común para los calendarios). En cualquier punto dado, sabemos cómo expresar el factor de descuento, r _i expresado en términos de X, usando interpolación lineal. Nuestra ecuación resulta ser con una sola incógnita y se puede resolver usando métodos numéricos. Cómo hacer esto: vea el código Python .

Entonces, sabemos cómo encontrar el valor de nuestra tasa en el punto 1 año. Usando el supuesto de interpolación lineal y basado en el valor swap que conocemos del mercado, encontraremos nuestro valor para X. Aquí trazamos la primera sección de nuestra curva:

Ahora, para calcular el precio del swap para dos años, necesitamos el valor en el punto 6 meses, 12 meses, 18 meses y 2 años. Usaremos exactamente la misma suposición que la última vez. Llamemos al valor de la tasa deseada Y y también usemos el supuesto sobre la línea de interpolación, restaurando la segunda sección de la curva. Así, paso a paso, llegaremos al final, hasta el punto de 10 años.

Este método se llama bootstrap . No es perfecto ni el único correcto, pero es lo suficientemente simple de implementar y comprender: el método bootstrap es excelente como nivel inicial.

Encontramos la curva de descuento. ¿Qué nos aporta? Formalmente hablando, estos son los valores de la tasa a un día en cualquier momento en el futuro hasta diez años. Probablemente pregunte: "¿Quién lo necesita?" De hecho, es difícil imaginar un escenario en el que un cliente se acerque a usted y le diga: "Quiero abrir un depósito de un día, que comenzará en 567 días". Esta es una situación bastante incomprensible, y no se debe percibir la curva construida de una forma tan directa.

Imaginemos que tenemos algún tipo de pago en el futuro, digamos siete años y medio. Pregunta: ¿cómo sabemos su valor actual?

Ésta es exactamente la pregunta que responderá la curva de descuento. Iremos a lo largo de cada punto de la curva, calcularemos el factor de descuento en cada punto y finalizaremos nuestro viaje en el punto durante siete años y medio, encontraremos el factor de descuento resultante, multiplicaremos por el pago; este será un precio honesto.

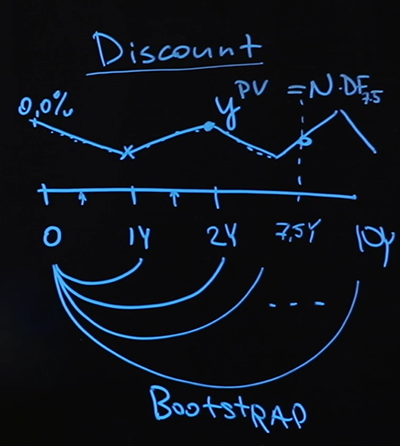
El modelo que utilicé, es decir, las tasas flotantes que tomé, cómo interpolé los valores intermedios y, en general, el hecho de que elegí la interpolación estuvo muy determinado por el tipo de datos que tengo. Tenía muy pocos datos: solo una tasa base y valores de intercambio. Si tengo más datos disponibles o si son diferentes, lo más probable es que cambie el modelo. Pero el método bootstrap (cuando traza la curva primero en una sección corta y luego traza más y más, confiando en los valores obtenidos previamente) todavía se aplica.

Ahora bien, recuerde que además de las curvas de descuento, necesitamos curvas LIBOR (TIBOR, EURIBOR, etc.). La diferencia estará en qué herramientas agregamos a nuestro modelo para el cálculo. Buscaremos contratos que contengan LIBOR y de forma similar, utilizando el método bootstrap, reconstruiremos la curva LIBOR.

Si tiene que construir una curva LIBOR real, tenga mucho cuidado con las herramientas que usa para construirla, evalúe cuidadosamente el modelo que usará. En este caso, utilicé el descuento nocturno, pero se necesita un método diferente para construir la curva LIBOR. Lo más probable es que el descuento sea cada tres o seis meses, según el instrumento. Si tiene suficientes datos, puede trazar una curva LIBOR, una curva EURIBOR, una curva TIBOR y cualquier otra.

Si un cliente acude a usted con las palabras: “Quiero un swap de tasa de interés no por diez años, sino por 134 meses, en el cual pagaré la LIBOR flotante cada 25 días”, esto no es un problema. Tenemos una curva LIBOR, utilizamos el supuesto de interpolación, podemos restaurar el valor LIBOR en cualquier punto. Conocemos el valor de la curva de descuento en cada punto, también podemos calcular todos los pagos y encontrar el precio mismo del "tramo" fijo que equilibra estos pagos flotantes. Por lo tanto, puede encontrar los valores del precio justo para absolutamente cualquier instrumento trazando varias curvas.

Así que repasemos los aspectos más destacados nuevamente. Tomé los datos disponibles y formulé algunas suposiciones. Primero, el calendario de pagos: con qué frecuencia, con qué frecuencia, cada parte paga un tramo fijo y uno flotante. En segundo lugar, ¿cómo calcularé la apuesta en la pierna flotante? El tercer supuesto se refiere a la interpolación de apuestas lineal. Utilizando estos tres supuestos, formulé varias ecuaciones no lineales, que resolví numéricamente. El cuaderno Jupyter se puede encontrar aquí. Secuencialmente, comenzando desde el segmento más corto de un año, luego dos años, tres, etc., reconstruí la curva para un intervalo de hasta 10 años. Esta es mi curva de descuento que puedo usar para evaluar cualquier instrumento. Este método se llama bootstrap: el segmento de la curva, que conté al principio, lo uso en el segundo paso, de lo contrario,lo que obtuve en el segundo paso, lo uso para el tercer paso y así sucesivamente, hasta que la curva esté completamente formada.

Espero que ahora ya no “flotes” en el tema de las tasas de interés flotantes y entre las tasas de interés de los swaps puedas encontrar vainilla. Y también puede construir cualquier curva usando el método bootstrap.

Todos los artículos de esta serie

Construcción de la curva de descuento. Programa educativo para geek, parte 5

More articles: