
Armored Warfare: Project Armata es un juego de acción de tanques en línea gratuito desarrollado por Allods Team, el estudio de juegos MY.GAMES. A pesar de que el juego está hecho en CryEngine, un motor bastante popular con un buen render en tiempo real, para nuestro juego tenemos que modificar y crear mucho desde cero. En este artículo, quiero hablar sobre cómo implementamos la aberración cromática para la vista en primera persona, y qué es.
¿Qué es la aberración cromática?
La aberración cromática es un defecto de la lente en el que no todos los colores llegan al mismo punto. Esto se debe al hecho de que el índice de refracción del medio depende de la longitud de onda de la luz (ver dispersión ). Por ejemplo, así es como se ve la situación cuando la lente no sufre de aberración cromática:
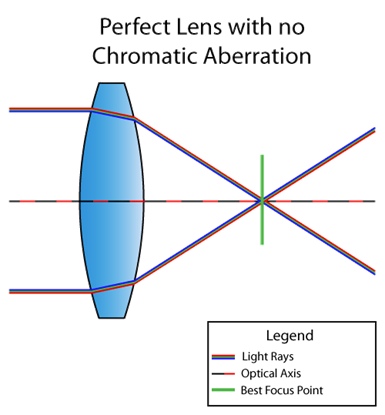
Y aquí hay una lente con un defecto:
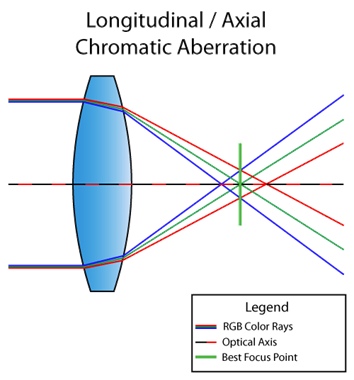
Por cierto, la situación anterior se llama aberración cromática longitudinal (o axial). Ocurre cuando diferentes longitudes de onda no convergen en el mismo punto en el plano focal después de pasar a través de la lente. Entonces el defecto es visible en toda la imagen:

En la imagen de arriba, puede ver que los colores púrpura y verde se destacan debido a un defecto. ¿No pueden ver? ¿Y en esta foto?

También hay aberración cromática lateral (o lateral). Ocurre cuando la luz incide en un ángulo a la lente. Como resultado, diferentes longitudes de onda de luz convergen en diferentes puntos en el plano focal. Aquí hay una foto para que entiendas:
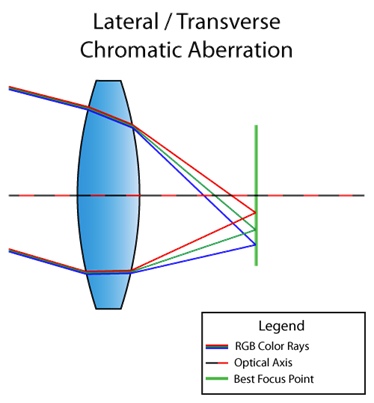
Ya puede ver en el diagrama que como resultado obtenemos una descomposición completa de la luz de rojo a violeta. A diferencia de la longitudinal, la aberración cromática lateral nunca aparece en el centro, solo más cerca de los bordes de la imagen. Para que entiendan lo que quiero decir, aquí hay otra imagen de Internet:

Bueno, ya que hemos terminado con la teoría, vayamos al grano.
Aberración cromática lateral con descomposición ligera
Comenzaré con el hecho de que responderé a la pregunta que podría surgir en la cabeza de muchos de ustedes: "¿CryEngine no implementa la aberración cromática?" Ahi esta. Pero se usa en la etapa de postprocesamiento en el mismo sombreador con nitidez, y el algoritmo se ve así ( enlace al código ):
screenColor.r = shScreenTex.SampleLevel( shPointClampSampler, (IN.baseTC.xy - 0.5) * (1 + 2 * psParams[0].x * CV_ScreenSize.zw) + 0.5, 0.0f).r;
screenColor.b = shScreenTex.SampleLevel( shPointClampSampler, (IN.baseTC.xy - 0.5) * (1 - 2 * psParams[0].x * CV_ScreenSize.zw) + 0.5, 0.0f).b;Que, en principio, funciona. Pero tenemos un juego sobre tanques. Necesitamos este efecto solo para la vista en primera persona, y solo para la belleza, es decir, para que todo esté enfocado en el centro (hola a la aberración lateral). Por lo tanto, la implementación actual no se ajustaba al menos al hecho de que su efecto fuera visible en toda la imagen.
Así es como se veía la aberración en sí misma (atención al lado izquierdo):

Y así es como se ve si gira los parámetros:

Por lo tanto, nos hemos fijado como nuestro objetivo:
- Implemente una aberración cromática lateral para que todo esté enfocado cerca del alcance, y si los defectos de color característicos no son visibles en los lados, entonces al menos deben ser borrosos.
- Muestree una textura multiplicando canales RGB por coeficientes correspondientes a una longitud de onda específica. Todavía no he hablado de esto, así que ahora puede que no esté completamente claro de qué se trata este punto. Pero definitivamente lo consideraremos en todos los detalles más adelante.
Primero, veamos el mecanismo general y el código para crear una aberración cromática lateral.
half distanceStrength = pow(length(IN.baseTC - 0.5), falloff);
half2 direction = normalize(IN.baseTC.xy - 0.5);
half2 velocity = direction * blur * distanceStrength;
Entonces, primero, se construye una máscara circular, que es responsable de la distancia desde el centro de la pantalla, luego se calcula la dirección desde el centro de la pantalla y luego se multiplica todo esto
blur. Blury falloff- estos son parámetros que se pasan desde el exterior y son solo multiplicadores para ajustar la aberración. Además, se lanza un parámetro desde el exterior sampleCount, que es responsable no solo del número de muestras, sino también, de hecho, del paso entre los puntos de muestreo, ya que
half2 offsetDecrement = velocity * stepMultiplier / half(sampleCount);
Ahora solo tenemos que ir
sampleCountuna vez desde este punto de la textura, cambiando cada vez por offsetDecrement, multiplicar los canales por los pesos de onda correspondientes y dividir por la suma de estos pesos. Bueno, es hora de hablar sobre el segundo punto de nuestro objetivo global.
El espectro visible de la luz varía de 380 nm (violeta) a 780 nm (rojo). Y he aquí, la longitud de onda se puede convertir a paleta RGB. En Python, el código que hace esta magia se ve así:
def get_color(waveLength):
if waveLength >= 380 and waveLength < 440:
red = -(waveLength - 440.0) / (440.0 - 380.0)
green = 0.0
blue = 1.0
elif waveLength >= 440 and waveLength < 490:
red = 0.0
green = (waveLength - 440.0) / (490.0 - 440.0)
blue = 1.0
elif waveLength >= 490 and waveLength < 510:
red = 0.0
green = 1.0
blue = -(waveLength - 510.0) / (510.0 - 490.0)
elif waveLength >= 510 and waveLength < 580:
red = (waveLength - 510.0) / (580.0 - 510.0)
green = 1.0
blue = 0.0
elif waveLength >= 580 and waveLength < 645:
red = 1.0
green = -(waveLength - 645.0) / (645.0 - 580.0)
blue = 0.0
elif waveLength >= 645 and waveLength < 781:
red = 1.0
green = 0.0
blue = 0.0
else:
red = 0.0
green = 0.0
blue = 0.0
factor = 0.0
if waveLength >= 380 and waveLength < 420:
factor = 0.3 + 0.7*(waveLength - 380.0) / (420.0 - 380.0)
elif waveLength >= 420 and waveLength < 701:
factor = 1.0
elif waveLength >= 701 and waveLength < 781:
factor = 0.3 + 0.7*(780.0 - waveLength) / (780.0 - 700.0)
gamma = 0.80
R = (red * factor)**gamma if red > 0 else 0
G = (green * factor)**gamma if green > 0 else 0
B = (blue * factor)**gamma if blue > 0 else 0
return R, G, B
Como resultado, obtenemos la siguiente distribución de color:

En resumen, el gráfico muestra cuánto y de qué color está contenido una onda con una longitud específica. En el eje de ordenadas, solo obtenemos los mismos pesos de los que hablé anteriormente. Ahora podemos implementar completamente el algoritmo, teniendo en cuenta lo indicado anteriormente:
half3 accumulator = (half3) 0;
half2 offset = (half2) 0;
half3 WeightSum = (half3) 0;
half3 Weight = (half3) 0;
half3 color;
half waveLength;
for (int i = 0; i < sampleCount; i++)
{
waveLength = lerp(startWaveLength, endWaveLength, (half)(i) / (sampleCount - 1.0));
Weight.r = GetRedWeight(waveLength);
Weight.g = GetGreenWeight(waveLength);
Weight.b = GetBlueWeight(waveLength);
offset -= offsetDecrement;
color = tex2Dlod(baseMap, half4(IN.baseTC + offset, 0, 0)).rgb;
accumulator.rgb += color.rgb * Weight.rgb;
WeightSum.rgb += Weight.rgb;
}
OUT.Color.rgb = half4(accumulator.rgb / WeightSum.rgb, 1.0);
Es decir, la idea es que cuanto más tenemos
sampleCount, menos paso tenemos entre los puntos de muestra y más dispersamos la luz (tenemos en cuenta más ondas con diferentes longitudes).
Si todavía no está claro, entonces vamos a ver un ejemplo específico, es decir, nuestro primer intento, y voy a explicar por qué tomar para
startWaveLengthy endWaveLength, y cómo se implementarán las funciones GetRed(Green, Blue)Weight.
Ajustando todo el espectro visible
Entonces, del gráfico anterior, conocemos la relación aproximada y los valores aproximados de la paleta RGB para cada longitud de onda. Por ejemplo, para una longitud de onda de 380 nm (violeta) (ver el mismo gráfico), vemos que RGB (0.4, 0, 0.4). Son estos valores los que tomamos para los pesos de los que hablé anteriormente.
Ahora tratemos de deshacernos de la función de obtener color mediante un polinomio de cuarto grado para que los cálculos sean más baratos (no somos un estudio de Pixar, sino un estudio de juegos: cuanto más baratos sean los cálculos, mejor). Este polinomio de cuarto grado debe aproximarse a los gráficos resultantes. Para construir el polinomio, utilicé la biblioteca SciPy:
wave_arange = numpy.arange(380, 780, 0.001)
red_func = numpy.polynomial.polynomial.Polynomial.fit(wave_arange, red, 4)
Como resultado, se obtiene el siguiente resultado (he dividido en 3 gráficos separados que corresponden a cada canal separado, de modo que es más fácil comparar con el valor exacto):
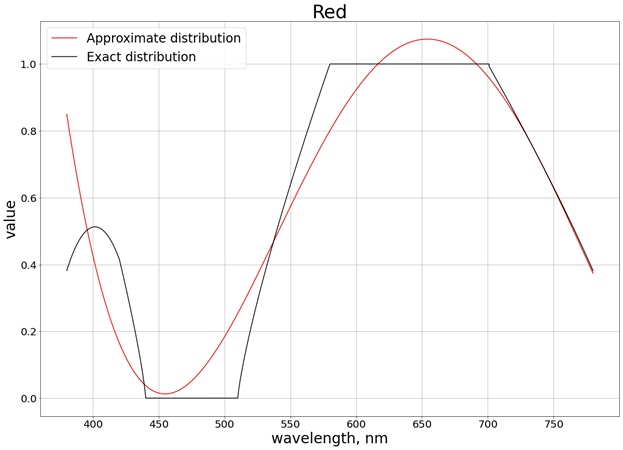
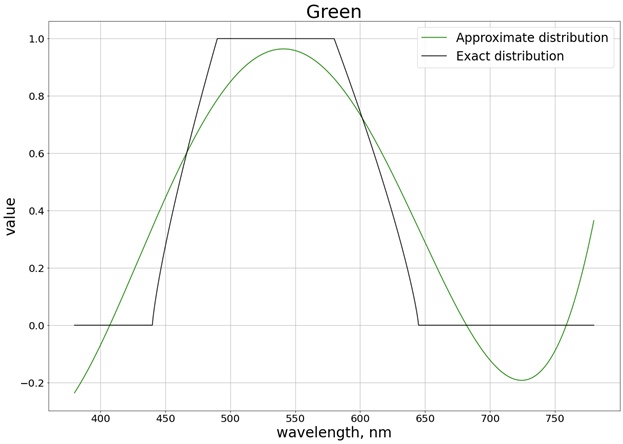
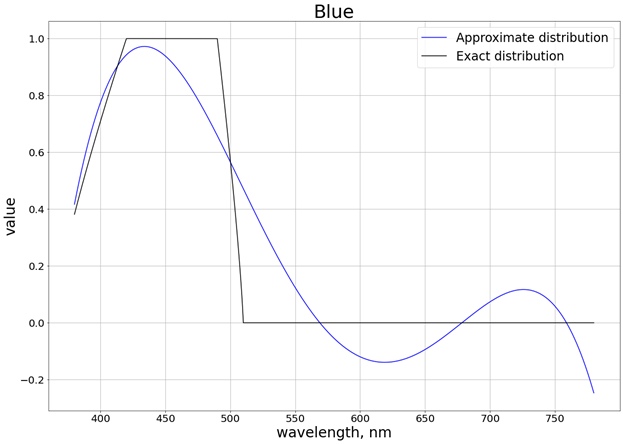
Para garantizar que los valores no superen el límite del segmento [0, 1], utilizamos la función
saturate. Para el rojo, por ejemplo, se obtiene la función:
half GetRedWeight(half x)
{
return saturate(0.8004883122689207 +
1.3673160565954385 * (-2.9000047500568042 + 0.005000012500149485 * x) -
1.244631137356407 * pow(-2.9000047500568042 + 0.005000012500149485 * x, 2) - 1.6053230172845554 * pow(-2.9000047500568042 + 0.005000012500149485*x, 3)+ 1.055933936470091 * pow(-2.9000047500568042 + 0.005000012500149485*x, 4));
}
Los parámetros que faltan
startWaveLengthy endWaveLengthen este caso son 780 nm y 380 nm, respectivamente. El resultado en la práctica sampleCount=3es el siguiente (ver los bordes de la imagen):

Si modificamos los valores, aumentamos
sampleCounta 400, entonces todo se vuelve mejor:

Desafortunadamente, tenemos un render en tiempo real en el que no podemos permitir 400 muestras (aproximadamente 3-4) en un sombreador. Por lo tanto, redujimos ligeramente el rango de longitud de onda.
Parte del espectro visible.
Tomemos un rango para que terminemos con los colores rojo puro y azul puro. También rechazamos la cola roja de la izquierda, ya que afecta en gran medida el polinomio final. Como resultado, obtenemos la distribución en el segmento [440, 670]:

Además, no es necesario interpolar sobre todo el segmento, ya que ahora podemos obtener un polinomio solo para el segmento donde cambia el valor. Por ejemplo, para el color rojo, este es el segmento [510, 580], donde el valor de peso varía de 0 a 1. En este caso, puede obtener un polinomio de segundo orden, que
saturatetambién se reduce por la función al rango de valores [0, 1]. Para los tres colores obtenemos el siguiente resultado teniendo en cuenta la saturación:

Como resultado, obtenemos, por ejemplo, el siguiente polinomio para rojo:
half GetRedWeight(half x)
{
return saturate(0.5764348105166407 +
0.4761860550080825 * (-15.571636738012254 + 0.0285718367412005 * x) -
0.06265740390367036 * pow(-15.571636738012254 + 0.0285718367412005 * x, 2));
}
Y en la práctica con
sampleCount=3:

En este caso, con los ajustes retorcidos, se obtiene aproximadamente el mismo resultado que al tomar muestras en todo el rango del espectro visible:

Por lo tanto, con polinomios de segundo grado, obtuvimos un buen resultado en el rango de longitud de onda de 440 nm a 670 nm.
Mejoramiento
Además de optimizar los cálculos por polinomios, puede optimizar el trabajo del sombreador, confiando en el mecanismo que establecimos en base a nuestra aberración cromática lateral, es decir, no realice cálculos en el área donde el desplazamiento total no va más allá del píxel actual, de lo contrario, tomaremos muestras del mismo píxel, y lo entendemos.
Se parece a esto:
bool isNotAberrated = abs(offsetDecrement.x * g_VS_ScreenSize.x) < 1.0 && abs(offsetDecrement.y * g_VS_ScreenSize.y) < 1.0;
if (isNotAberrated)
{
OUT.Color.rgb = tex2Dlod(baseMap, half4(IN.baseTC, 0, 0)).rgb;
return OUT;
}
La optimización es pequeña, pero muy orgullosa.
Conclusión
La aberración cromática lateral en sí misma se ve muy fría; este defecto no interfiere con la vista en el centro. La idea de descomponer la luz en pesas es un experimento muy interesante que puede dar una imagen completamente diferente si su motor o juego permite más de tres muestras. En nuestro caso, era posible no molestarnos y encontrar un algoritmo diferente, ya que incluso con las optimizaciones no podemos permitirnos muchas muestras y, por ejemplo, la diferencia entre 3 y 5 muestras no es muy visible. Puede experimentar con el método descrito usted mismo y ver los resultados.