
La optimización en los negocios en la abrumadora mayoría de los casos está asociada con el uso del método de programación lineal. El método es bastante sencillo. Además, existe un teorema sobre la existencia y la unicidad de la solución.
Sin embargo, en la práctica, no todo es del todo simple.
El primer problema es la no linealidad de las condiciones del mundo real. Para que el método de programación lineal sea aplicable, deben linealizarse. Hay formas de establecer plausiblemente la no linealidad a través de ecuaciones lineales y desigualdades mediante la introducción de nuevas variables, el establecimiento de coeficientes de peso, etc. Al resolver problemas de producción, en este caso es necesario operar con un gran número de variables y, en consecuencia, ecuaciones (desigualdades).
En la teoría de resolver problemas extremos, existe un teorema sobre la estabilidad de las soluciones a los problemas de programación lineal. Según esto, la solución es estable solo si el dominio del problema es convexo. Con una gran cantidad de variables y desigualdades, no es posible establecer si el dominio del problema es convexo. Además, la probabilidad de no convexidad es alta.
Si el problema no es estable, entonces, dependiendo del punto de partida de atravesar los vértices, se obtendrán resultados diferentes.
Segundo problema- restricción de la variable desde abajo (x> h> 0). Cualquier implementación de un método de programación lineal siempre proporcionará un valor x distinto de cero. Si x es exactamente igual a h, esto significa que el valor de la variable x debería ser esencialmente cero. En la práctica, tales volúmenes "ficticios" (curtosis del método) se encuentran dispersos en variables "significativas". La consecuencia de esta práctica es la erosión del concepto de una solución óptima, que es especialmente importante si dicha solución es una de las muchas en la cadena de decisión.
El tercer problema es de gestión. El método de programación lineal da solo un resultado. ¿Y cómo mirar los resultados que están cerca de lo óptimo? Por ejemplo, en la solución resultante, la calificación del proveedor es baja. Cómo entender si existen soluciones cercanas, pero para proveedores confiables.
Tarea de transporte
El ejemplo corresponde a un problema de programación lineal de transporte.
Hay 5 transportistas (la tarea se estableció para el transporte de carbón), que tienen dos cálculos de tarifas. Los límites arancelarios y las tarifas en sí pueden modificarse (se establecen paramétricamente).

El transporte se especifica como punto a punto (de acuerdo con el método aceptado para el transporte de carbón) y el volumen.
Vista general de la interfaz.

Área de asignación de transporte.
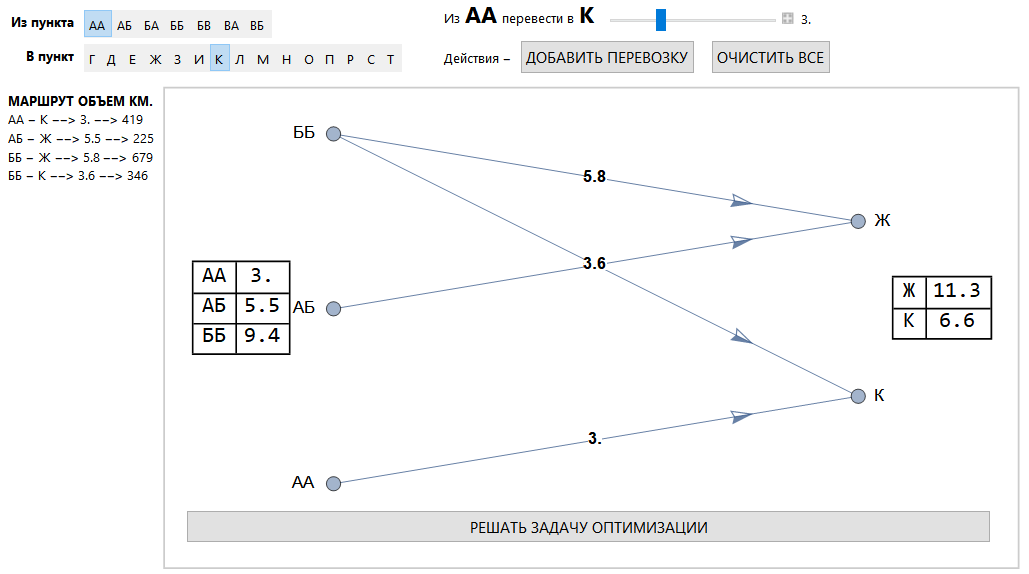
Método de solución de clúster
En lugar de un problema de programación lineal, se resuelve un grupo de problemas, cuyo número corresponde a todas las combinaciones posibles de tarifas. En el envío anterior, hay 127 de ellos (segundo valor en el rectángulo superior izquierdo).

Las soluciones óptimas se seleccionan del conjunto de los problemas correctos restantes. Cada tarea proporciona una solución óptima para una combinación específica de tarifas. Las soluciones presentadas anteriormente constituyen un cierto rango de máximos.
Por qué el método de clúster es bueno:
- aparece la comprensión de la estabilidad de la solución.
- no hay volúmenes "ficticios" para las variables limitadas desde abajo, ya que habrá otra combinación en la que dicha condición esté ausente (dado que dicha variable está ausente).
- Las condiciones subjetivas (calificaciones, preferencias) pueden introducirse utilizando el método de programación lineal estándar.
Con un mayor número de envíos, tenemos la siguiente imagen (fragmento).
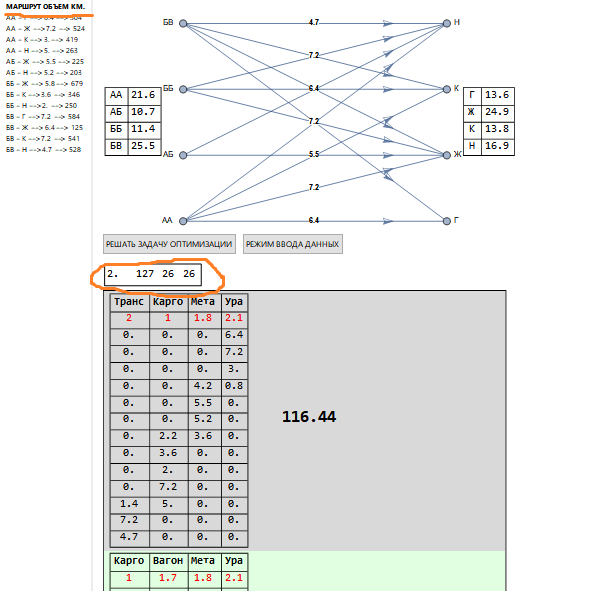
En la esquina superior izquierda en el rectángulo arriba de las soluciones (resaltado en naranja), se indican otros valores que antes: 127 - combinaciones (como antes, que están relacionadas con la estructura de escalas arancelarias), 26 - corresponde al número de problemas correctos que se están resolviendo. La tarifa utilizada se indica en rojo debajo del nombre del transportista, y las columnas de transporte corresponden a la lista de rutas (subrayadas en naranja).
Es importante tener en cuenta que el método utilizado le permite comprender el resultado, evaluar soluciones similares y utilizar su experiencia profesional al elegir alternativas, teniendo en cuenta las complejidades de administrar un negocio en particular.