Joshua Green y Andrew Lobb, aburridos en cuarentena, descubrieron cómo probar una de las variantes del teorema de la clavija rectangular

¿Se pueden encontrar todo tipo de rectángulos en un circuito cerrado?
A mediados de marzo, los matemáticos Joshua Green y Andrew Lobb se encontraron en una posición similar: encerrados dentro de cuatro paredes, tratando de adaptarse a la creciente epidemia de coronavirus. Decidieron lidiar con eso profundizando en su investigación.
"Creo que la pandemia fue una especie de catalizador para este proceso", dijo Greene, profesor del Boston College. "Decidimos que sería mejor realizar algún tipo de trabajo conjunto que pueda apoyarnos".
Uno de los problemas que los dos amigos decidieron abordar fue una variante de la cuestión geométrica que había permanecido sin respuesta durante más de cien años.
"Esta tarea es extremadamente simple de formular y comprender, pero es muy difícil de resolver" - dijoElizabeth Denn de Washington y Lee University.
Todo comienza con un bucle cerrado: cualquier ruta curva que tenga el mismo principio y fin. La tarea que Green y Lobb han asumido esencialmente argumenta que en cualquier camino hay conjuntos de cuatro puntos que forman los vértices de un rectángulo de cualquier proporción dada.
Y aunque este "problema de clavija rectangular" suena como una pregunta que cualquier estudiante de secundaria con una regla y una brújula puede manejar, se ha resistido a los intentos más persistentes de los matemáticos durante muchas décadas. Y cuando Green y Lobb se hicieron cargo, no tenían razón para esperar otra cosa.
Greene dijo que de todos los proyectos difíciles en los que trabajó, "este fue el menos prometedor en mi opinión".
Pero la pandemia creció, y Green y Lobb, que trabajan en la Universidad de Durham en Inglaterra y el Instituto de Ciencia y Tecnología de Okinawa, respectivamente, tuvieron conversaciones semanales con Zoom y rápidamente generaron varias ideas. Y luego, el 19 de mayo, cuando muchas partes del mundo reabrieron, publicaron su decisión .
Su prueba final, que muestra que efectivamente se pueden encontrar rectángulos, lleva este problema a un nivel geométrico completamente diferente. Y allí esta obstinada pregunta cede muy fácilmente.
"Es bastante extraño", dijo Richard Schwartz, de la Universidad de Brown. "Esta idea fue perfecta para esta tarea".
Repensando rectángulos
El problema de las clavijas rectangulares está estrechamente relacionado con la pregunta planteada por el matemático alemán Otto Töplitz en 1911. Él predijo que en cualquier curva cerrada puedes encontrar cuatro puntos, conectando los cuales puedes obtener un cuadrado. Esta pregunta suya sobre "clavijas cuadradas" permanece abierta.
"Esta es una tarea vieja y frustrante que no puede ser pirateada de ninguna manera", dijo Green.
Para comprender la complejidad del problema, es importante conocer las propiedades de las curvas que se consideran en el problema de la clavija cuadrada; esto también es importante para la prueba de Green y Lobb.
Esta pareja resolvió el problema de las curvas cerradas, tanto "continuas" como "suaves". La continuidad significa que no hay descansos. La suavidad significa continuidad y sin esquinas. Es probable que dibujes una curva suave y continua si te sientas en tu escritorio con papel y lápiz. Son "más fáciles de trabajar", dijo Green.
Las curvas continuas suaves son diferentes de las curvas simplemente continuas, pero no suaves, como las involucradas en la conjetura de Toeplitz de clavijas cuadradas. Tal curva puede tener esquinas, puntos en los que la curva se desvía repentinamente y va en una dirección diferente. Un buen ejemplo de una curva con muchos ángulos es la curva de Koch fractal con forma de copo de nieve ., de hecho, que consta de algunas esquinas. El copo de nieve de Koch y otras curvas similares no pueden analizarse utilizando métodos algebraicos, lo que los hace especialmente difíciles de estudiar.
"Algunas curvas continuas [no suaves] son simplemente desagradables", dijo Denn.
Aún así, el problema resuelto por Green y Lobb pertenece a curvas suaves y, por lo tanto, continuas. Y en lugar de averiguar si siempre hay cuatro puntos en tales curvas que forman un cuadrado (para curvas continuas suaves, este problema se resolvió en 1929), estudiaron algo más: ¿siempre hay cuatro puntos en tales curvas que forman un rectángulo de cualquier dado? proporciones, es decir con cualquier relación de aspecto. Para un cuadrado, esta relación es 1: 1, para televisores de alta definición - 16: 9.

El primer gran avance en el problema de las clavijas rectangulares fue la evidencia encontrada a fines de la década de 1970 por Herbert Vaughn. Ofreció una nueva forma de ver la geometría de los rectángulos y proporcionó varios métodos que luego fueron utilizados por otros matemáticos, incluidos Green y Lobb.
"Todos conocen esta prueba", dijo Green. "Es casi folklórico, aprendes sobre esas cosas al discutir todo en la mesa".
En lugar de imaginar un rectángulo como cuatro puntos conectados, Vaughn lo imaginó como dos pares de puntos en una relación entre sí.

Imagina un rectángulo con vértices ABCD. En él, la distancia entre los puntos AC (en la diagonal) es igual a la distancia entre los puntos BD (en la otra diagonal). Además, estas diagonales se cruzan exactamente en el medio.
Por lo tanto, al buscar rectángulos en un bucle cerrado, puede buscar pares de puntos que se encuentran en los extremos de los mismos segmentos de línea que se cruzan en el medio. Para encontrarlos, es importante encontrar una forma sistemática de describirlos.
Para entender lo que esto significa, comencemos con algo más simple. Toma la recta numérica. Elija dos puntos en él, digamos los números 7 y 8, y construyémoslos como un punto en el plano numérico (7, 8). También podemos construir puntos que son un par de números idénticos (7, 7). Ahora consideremos todos los pares posibles de números que se pueden encontrar en la recta numérica (¡y hay muchos de ellos!). Si construimos todos los pares de tales números, entonces llenaremos el plano numérico completo. Otra forma de expresar esto es decir que el plano numérico se "parametriza", es decir, recoge todos los pares de números en la línea numérica de manera ordenada.
Vaughn hizo algo similar con pares de puntos en una curva cerrada. Al igual que la recta numérica, unidimensional, solo se cierra sobre sí misma. Se dio cuenta de que si toma pares de puntos con una curva y construye una figura a partir de ellos (y no importa cuál sea la coordenada xy cuál sea la y), entonces el plano no funcionará. En cambio, obtienes una figura inesperada: una tira de Mobius , una superficie bidimensional con solo un lado.

Y en cierto sentido, esto es bastante lógico. Para entender por qué, seleccione un par de puntos en la curva y asígneles el nombre x e y. Ahora muévase de x a y, moviéndose a lo largo de una parte de la curva, y simultáneamente, de y a x, moviéndose a lo largo de lo opuesto. En el proceso, pasará por todos los pares de puntos en la curva, comenzando y terminando en un par desordenado (x, y). Pero esto lo regresará al principio: solo la secuencia final de puntos será opuesta a la inicial. Un bucle de puntos desordenados que cambian de orientación al opuesto es la esencia de la tira de Möbius.
Esta cinta les da a los matemáticos un nuevo objeto que puede analizarse como parte del problema de la clavija rectangular. Vaughn usó este hecho para demostrar que en cualquier curva hay al menos un conjunto de cuatro puntos que forman un cuadrado.
Respuestas de cuatro dimensiones
La prueba de Green y Lobb se basa en el trabajo de Vaughn. Sin embargo, también combina varios hallazgos adicionales, algunos de los cuales son relativamente recientes. La prueba final es como un instrumento preciso, cuyo resultado deseado se basa en una combinación de ideas cuidadosamente considerada.
Uno de los primeros ingredientes principales de su prueba llegó en noviembre de 2019, cuando el estudiante de doctorado de la Universidad de Princeton, Cole Hugelmeyer, publicó el documento.demostrando una nueva forma de analizar la tira de Möbius utilizada por Vaughn. Usó un proceso matemático conocido como anidamiento, que es cuando tomamos un objeto y lo proyectamos en un espacio geométrico. Como resultado, Green y Lobb tomaron la técnica de Hugelmeyer y la transfirieron a otro espacio geométrico. Pero para entender lo que hicieron, primero debes entender lo que hizo.
Aquí hay un ejemplo simple de anidamiento.
Comencemos con una línea unidimensional. Cada punto de una línea recta está definido por un solo número. Ahora incrustaremos esta línea en un espacio bidimensional, es decir, la dibujaremos en un plano.
Después de incrustar una línea recta en el plano xy, cada punto ya está determinado por dos números: las coordenadas x e y, que describen dónde está exactamente el punto en el plano. Ahora puede analizar la línea utilizando técnicas de geometría 2D.
La idea de Hugelmeyer era tomar algo como una tira de Mobius, pero incrustarla en un espacio de 4, donde las propiedades de la geometría de 4 dimensiones le permitirán probar los resultados que desea.
“Básicamente, tienes una tira de Mobius y necesitas asignar cuatro coordenadas a cada punto. Será algo así como la dirección de un punto en el espacio de cuatro dimensiones ", dijo Lobb.
Hugelmeyer asignó estas direcciones de tal manera que fue más fácil llegar al objetivo principal, encontrar rectángulos en una curva. Podemos decir que asignó a cada punto de la curva algo así como una dirección postal: estado, ciudad, nombre de la calle y número de casa.
Para hacer esto, comenzó desde un punto específico en la tira de Mobius y tomó los dos puntos en la curva cerrada original que ella denotó. Luego encontró el punto medio del segmento de línea que conecta estos puntos, y determinó sus coordenadas x e y. Obtuvimos los dos primeros valores de la dirección de cuatro dimensiones (estado y ciudad).
Luego midió la distancia entre los dos puntos originales en la curva. Esta longitud se convirtió en el tercer valor de la dirección de cuatro dimensiones (nombre de la calle). Finalmente, calculó el ángulo entre el segmento de línea que conecta los dos puntos originales y el eje x. Este ángulo se convirtió en el cuarto valor de la dirección de cuatro dimensiones (número de casa). Estos cuatro valores le dicen todo sobre un par de puntos en la curva.

Este ejercicio suena bastante desafiante, pero valió la pena rápidamente. Hugelmeyer tomó la tira de Mobius adjunta y la giró. La tira de Mobius rotada se ha movido en relación con su posición original, y las dos copias de la tira se cruzan. Dado que el giro tuvo lugar en un espacio de cuatro dimensiones, la forma de auto-intersección de la tira de Möbius es difícil de imaginar, pero es fácil de describir matemáticamente.
Esta intersección fue de gran importancia. Cuando dos copias de la tira de Mobius se superponen entre sí, se pueden encontrar dos pares de puntos en la curva cerrada original, formando los cuatro vértices del rectángulo.
¿Por qué?
Primero, recuerde que un rectángulo puede representarse como dos pares de puntos con un centro común de intersección de segmentos de la misma longitud que los conecta. Es esta información la que está codificada en los primeros tres valores de la dirección de cuatro dimensiones asignada a cada punto de la tira de Möbius anidada.
En segundo lugar, en un espacio de cuatro dimensiones, puede desplegar la tira de Möbius de tal manera que cambie solo una de las coordenadas de cada punto en su dirección de cuatro dimensiones: el número de casa cambia, pero la calle, la ciudad y el estado permanecen. Como ejemplo, recuerde que si toma un ladrillo, colóquelo frente a usted y luego muévalo hacia la derecha, solo cambiará su coordenada x, pero no y o z.
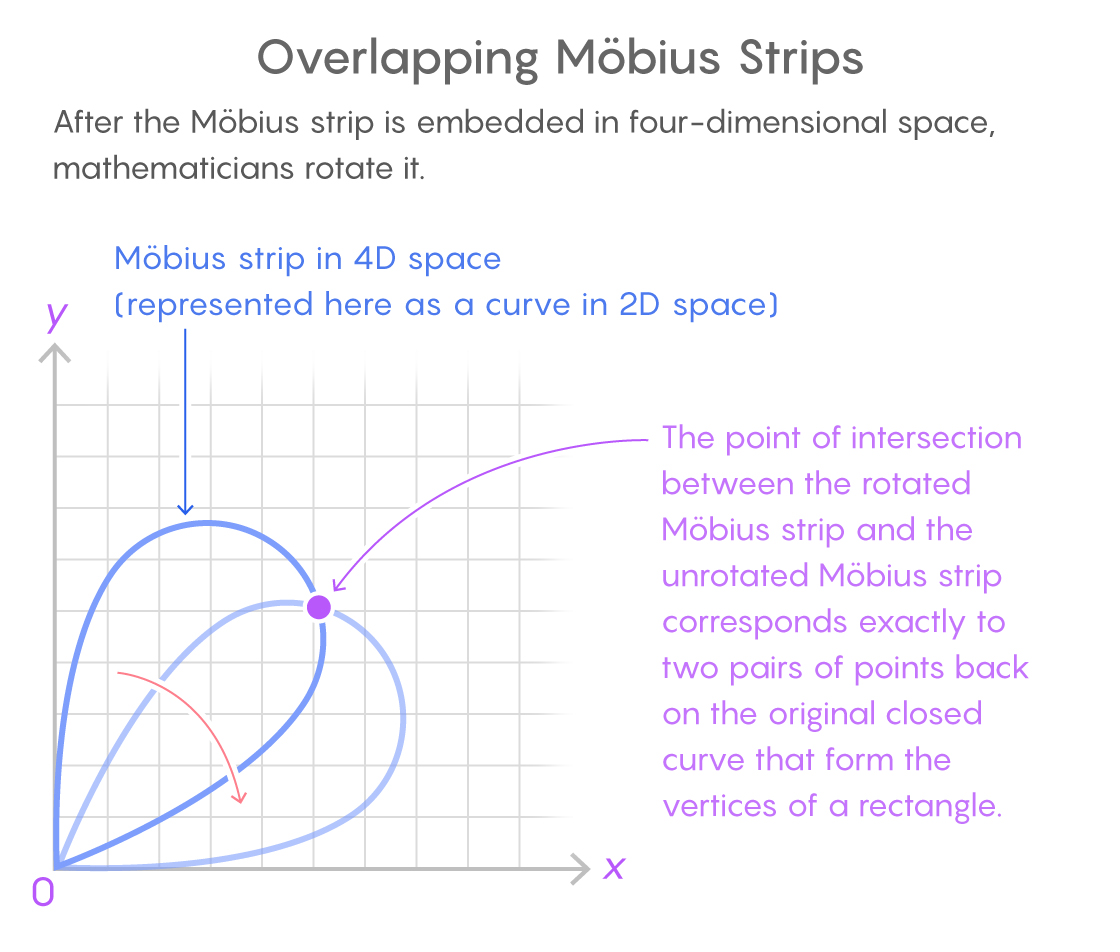
La tira de Möbius en el espacio de cuatro dimensiones se indica aquí mediante una curva de dos dimensiones. El punto de intersección de las dos copias corresponde a dos pares de puntos en la curva cerrada original que forman un rectángulo.
Hugelmeyer explicó cómo rotar la tira de Mobius en un espacio de cuatro dimensiones para que las dos coordenadas que indican el punto medio de los segmentos de línea que conectan pares no cambien, al igual que las coordenadas que indican la distancia entre pares de puntos. Su rotación cambió solo la última coordenada, que contiene información sobre el ángulo en el que se encuentra el segmento que conecta los puntos.
Como resultado, la intersección de la copia girada de la tira de Möbius y su original correspondía exactamente a dos pares de puntos ubicados en una curva cerrada, que tenían un centro común (intersecciones de los segmentos que los conectaban) y se ubicaban a la misma distancia entre sí. Es decir, esta intersección correspondía a los cuatro vértices del rectángulo en la curva.
La estrategia de usar la intersección de dos espacios para encontrar los puntos correctos se ha utilizado durante mucho tiempo en el trabajo sobre los problemas de las clavijas cuadradas y rectangulares.
"En la intersección de estos espacios está el deseado", dijo Denn. "Mucha de la evidencia de la historia de las clavijas cuadradas tiene esta idea".
Hugelmeyer utilizó una estrategia de intersección en un entorno de cuatro dimensiones y obtuvo más que nadie antes que él. La tira de Mobius se puede girar en cualquier ángulo de 0 ° a 360 °, y demostró que un tercio de todas estas rotaciones dan como resultado la intersección del original y la copia girada. Esto es equivalente a afirmar que puede encontrar rectángulos en una curva cerrada con un tercio de todas las relaciones de aspecto posibles.
"Le damos crédito a Cole por pensar en poner una tira de Mobius en el espacio 4D y usar técnicas 4D", dijo Green.
Al mismo tiempo, el resultado de Hugelmeier resultó ser provocativo: si el espacio de cuatro dimensiones es tan útil para esta tarea, ¿por qué fue útil solo para un tercio de todos los rectángulos?
"Después de todo, tiene que haber una manera de obtener los dos tercios restantes", dijo Green. - ¿Pero cómo?"
Enfoque simpléctico
Green y Lobb estaban interesados en el problema de las clavijas rectangulares incluso antes de que la pandemia los enviara a casa. En febrero, Lobb organizó una conferencia en el Instituto de Ciencia y Tecnología de Okinawa , a la que también asistió Green. La pareja pasó un par de días hablando sobre esta tarea. Después de eso, lo discutieron durante otra semana, en el camino viendo las vistas de Tokio.
"No hemos dejado de discutir este tema", dijo Lobb. "Fuimos a restaurantes, cafeterías, museos, y de vez en cuando teníamos pensamientos sobre esto".
Continuaron sus discusiones incluso después de ser encerrados en sus hogares. Esperaban demostrar que cualquier rotación de la tira de Mobius daría un punto de intersección, lo que equivale a encontrar rectángulos de cualquier proporción.
A mediados de abril, formaron una estrategia. Significaba incrustar la cinta en un tipo especial de espacio de cuatro dimensiones. La anidación regular implica que coloque el objeto deseado de cualquier manera. Imagine de cuántas maneras puede incrustar una curva cerrada unidimensional en un plano bidimensional: su número es infinito, ya que hay infinitas maneras en que puede colocar un hilo atado en un bucle sobre una mesa.
Pero supongamos que la superficie bidimensional en la que anida el bucle tiene su propia estructura. Imagine, por ejemplo, un mapa con flechas (o vectores) que nos indican en qué dirección y a qué velocidad sopla el viento en la superficie de la Tierra. Ahora tiene una superficie 2D con información adicional, o estructura, en cada punto.
Luego puede introducir restricciones: se debe colocar una solicitud de propuesta unidimensional en el mapa para que siempre siga las direcciones de las flechas en el mapa.
"Están limitando las cosas para que la curva siga estos vectores", dijo Schwartz. Y ahora tiene menos formas de colocar la curva.

Otros espacios geométricos pueden imponer diferentes restricciones. Importante para el trabajo de Green y Lobb fue el llamado. simpléctico espacio .
Este concepto geométrico apareció por primera vez en el siglo XIX al estudiar sistemas físicos como los planetas en órbita. La posición de un planeta que se mueve en un espacio tridimensional está determinada por tres coordenadas. Pero, como observó el matemático irlandés William Rowan Hamilton, en cada punto de la ruta de movimiento del planeta, también puede colocar un vector que denota su impulso.
En la década de 1980, el matemático soviético y ruso Vladimir Igorevich Arnold desarrolló el estudio de la geometría simpléctica . Se dio cuenta de que los espacios geométricos de una estructura simpléctica, cuando se giran, se cruzan entre sí con más frecuencia que los espacios que no tienen esa estructura.
Esto fue perfecto para Green y Lobb, ya que querían resolver el problema de la clavija rectangular para todas las proporciones, lo que demuestra que una copia rotada de una tira de Mobius de parametrización también se cruza con frecuencia. Entonces comenzaron a tratar de incrustar una tira de Möbius bidimensional en un espacio simpléctico de cuatro dimensiones. "Una idea radicalmente nueva era abordar este problema desde el punto de vista de la geometría simpléctica", dijo Green. "Y eso cambió todo".
A finales de abril, Green y Lobb determinaron que era posible incrustar una tira de Mobius en un espacio simpléctico de cuatro dimensiones para que se alineara con su estructura. Después de eso, podrían comenzar a usar herramientas de geometría simpléctica, muchas de las cuales están directamente relacionadas con la cuestión de las intersecciones propias.
"Si se puede hacer que la tira de Möbius siga reglas simplécticas, se pueden usar algunos de los teoremas simplécticos", dijo Lobb.
Green y Lobb confiaban en que podrían mejorar el resultado de Hugelmeyer, es decir, demostrar que la intersección se produce no solo en un tercio de todas las esquinas. Esto significará que desde los puntos de la curva será posible hacer rectángulos con más de un tercio de todas las proporciones posibles.
"Cuando tuvimos esta idea, quedó claro que algo iba a suceder", dijo Lobb.
Sin embargo, sus resultados resultaron ser más generales y aparecieron mucho más rápido de lo que esperaban. Todo gracias a un extraño objeto matemático: la botella de Klein , que en el contexto de la geometría simpléctica tiene una propiedad importante.
Conexión de botella Klein
La botella de Klein es una superficie bidimensional que parece una jarra modernista. Al igual que la tira de Mobius, tiene una sola superficie y se puede pegar dos tiras de Mobius. Cualquier botella de Klein que pueda recoger y colocar en su escritorio (como hacen muchos matemáticos) se cruza sobre sí misma. Es imposible colocar una botella de Klein en un espacio tridimensional para que no se cruce.
"La botella de Klein tiene que ser una superficie, pero su asa debe atravesar la botella para ir de afuera hacia adentro", dijo Schwartz.
Sin embargo, este no es necesariamente el caso. La botella de Klein se puede anidar en el espacio 4D para que no se cruce. La cuarta dimensión proporciona espacio para maniobrar, y la botella de Klein puede evitarse. Esto se puede comparar con cómo si dos personas caminan una hacia la otra en una línea unidimensional, no pueden evitar una colisión, pero si caminan en un piso bidimensional, pueden alejarse fácilmente.

En mayo, Green y Lobb recordaron un hecho sobre la botella de Klein: no se puede incrustar en un espacio simpléctico de cuatro dimensiones para que no se entrecruce [del trabajo de otro matemático ruso, Vsevolod Viktorovich Shevchishinsobre la incrustación lagrangiana de la botella de Klein en un espacio de cuatro dimensiones / aprox. traducción]. En otras palabras, no hay botella de Klein sin auto intersección que satisfaga todos los requisitos de un espacio simpléctico. Este hecho se convirtió en la clave de la prueba. "Era una varita mágica", dijo Green.
Y es por eso. Green y Lobb ya han demostrado que es posible incrustar una tira de Mobius en un espacio simpléctico de cuatro dimensiones para que satisfaga sus requisitos. Solo tenían que averiguar si cada vuelta de la tira de Mobius se cruza con la copia original.
Sin embargo, dos tiras de Mobius que se cruzan son equivalentes a una botella de Klein, que se cruza en ese espacio. Y si gira la tira de Mobius para que la copia rotada no se cruce con el original, obtendrá una botella de Klein que no se cruza. Pero esa botella de Klein no puede existir en un espacio simpléctico de cuatro dimensiones. Por lo tanto, cualquier posible rotación de la tira de Möbius anidada también debe intersectarse, es decir, en cada curva suave cerrada, se pueden encontrar cuatro puntos que forman un rectángulo de cualquier proporción.
El final de la prueba golpea al lector como una avalancha.
"Primero se configura, configura, configura y luego gruñe, y la prueba está lista", dijo Denn.
La prueba de Green y Lobb es un buen ejemplo de cómo resolver un problema a menudo se basa en encontrar el punto de vista correcto. Generaciones de matemáticos no han podido abordar esta versión del problema de la clavija rectangular porque han tratado de resolverlo en condiciones geométricas más tradicionales. Cuando Green y Lobb llevaron el problema al mundo simpléctico, se resolvió fácilmente.
"Estos problemas, que surgieron en las décadas de 1910 y 1920, no tenían una plataforma adecuada para reflexionar sobre ellos", dijo Green. "Y ahora estamos comenzando a comprender que, de hecho, son encarnaciones ocultas del fenómeno de la simplicidad".