Detección de colisión y el teorema del eje divisorio

Hoy en día, las computadoras son computadoras poderosas

capaces de realizar millones de operaciones por segundo. Y, naturalmente, no puedes prescindir de la simulación del mundo real o del juego. Uno de los problemas del modelado y la simulación por computadora es determinar la colisión de dos objetos, una de cuyas soluciones se realiza mediante el teorema en el eje de separación.







Nota. El artículo dará un ejemplo con 2 paralelepípedos (en adelante, cubos), pero se preservará la idea de otros objetos convexos.

Nota. Toda la implementación se realizará en Unity.

Acto 0. Teoría general

Primero, debe familiarizarse con el " teorema de separación del hiperplano ", que será la base del algoritmo.



Teorema. Dos geometrías convexas no se cruzan si y solo si hay un hiperplano entre ellas que las separa. El eje ortogonal al

hiperplano divisorio se llama eje divisorio, y las proyecciones de las figuras sobre él no se cruzan.





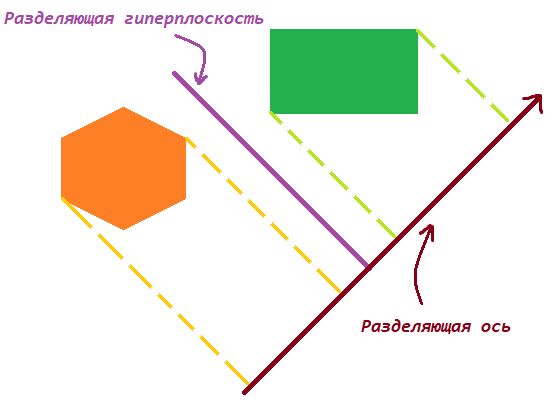
Eje de división (caso 2D)





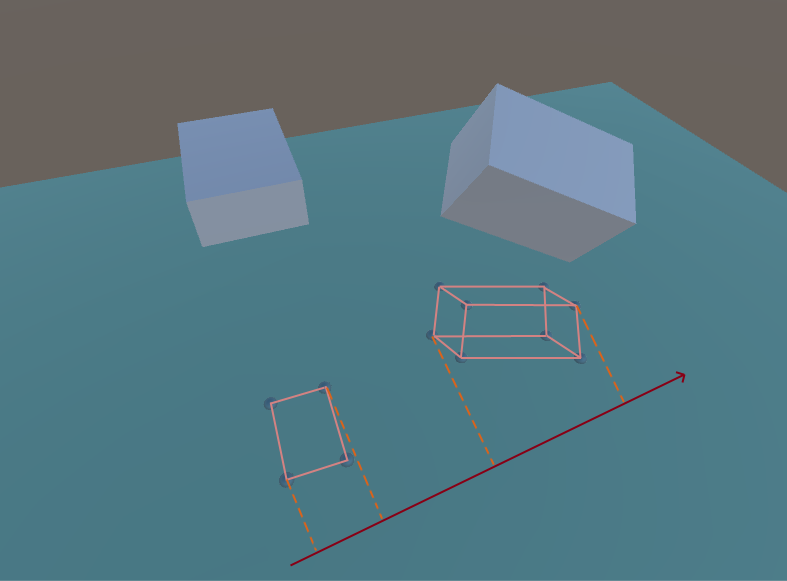
Eje de división (caso 3D)

Puede notar que las proyecciones en el eje de división no se cruzan.



Propiedad. El eje divisorio potencial estará en los siguientes conjuntos:

• Normas planas de cada cubo (rojo)
• Producto vectorial de los bordes de los cubos. $$$\{[\vec{x},\vec{y}] : x∈X, y∈Y\}$,

   donde X es los bordes del primer cubo (verde) e Y es el segundo (azul).







Podemos describir cada cubo con los siguientes datos de entrada:

• Coordenadas del centro del cubo
• Dimensiones del cubo (altura, ancho, profundidad)
• Quaternion del cubo

Creemos una clase adicional para esto, cuyas instancias proporcionarán información sobre el cubo.

public class Box
{
    public Vector3 Center;
    public Vector3 Size;
    public Quaternion Quaternion;

    public Box(Vector3 center, Vector3 size, Quaternion quaternion)
    {
       this.Center = center;
       this.Size = size;
       this.Quaternion = quaternion;
    }
    //  , 
    //      GameObject
    public Box(GameObject obj)
    {
        Center = obj.transform.position;
        Size = obj.transform.lossyScale;
        Quaternion = obj.transform.rotation;
    }

}

Acto 1. Cuaterniones

Como suele ser el caso, un objeto puede girar en el espacio. Para encontrar las coordenadas de los vértices, teniendo en cuenta la rotación del cubo, debes comprender qué es un cuaternión.



Quaternion es un número hipercomplejo que determina la rotación de un objeto en el espacio.

$$

$$w+xi+yj+zk$$

La parte imaginaria (x, y, z) representa un vector que define la dirección de rotación,

mientras que la parte real (w) define el ángulo en el que se realizará la rotación.



Su principal diferencia con todos los ángulos habituales de Euler es que es suficiente para nosotros tener un vector, que determinará la dirección de rotación, que tres vectores linealmente independientes que rotan el objeto en 3 subespacios.



Recomiendo dos artículos que detallan más sobre los cuaterniones:



Uno

Dos



Ahora que tenemos una comprensión mínima de los cuaterniones, comprendamos cómo rotar un vector y describamos la función de rotar un vector con un cuaternión.



Fórmula de rotación vectorial

$$

$$\vec{v}' = q * \vec{v} * \overline{q}$$

$$$\vec{v}'$ Es el vector requerido

$$$\vec{v}$ - vector original

$$$q$ - cuaternión

$$$\overline{q}$- Cuaternión inverso



Para empezar, demos el concepto de cuaternión inverso en una base ortonormal: es un cuaternión con una parte imaginaria del signo opuesto.



$$$q = w+xi+yj+zk$

$$$\overline{q} = w-xi-yj-zk$



Contemos $$$\vec{v} * \overline{q}$



$$$M = \vec{v}*\overline{q} = (0 + v_xi + v_yj + v_zk)(q_w - q_xi - q_yj - q_zk) =$

$$$=\color{red}{v_xq_wi} + \color{purple}{v_xq_x} - \color{blue}{v_xq_yk} + \color{green}{v_xq_zj} +$

$$$+\color{green}{v_yq_wj} + \color{blue}{v_yq_xk} + \color{purple}{v_yq_y} - \color{red}{v_yq_zi} +$

$$$+\color{blue}{v_zq_wk} - \color{green}{v_zq_xj} + \color{red}{v_zq_yi} + \color{purple}{v_zq_z}$



Ahora escribiremos los componentes individuales y de este producto recolectaremos un nuevo cuaternión.

$$$M = u_w+u_xi+u_yj+u_zk$

$$$u_w = \color{purple}{v_xq_x + v_yq_y + v_zq_z}$

$$$u_xi = \color{red}{(v_xq_w - v_yq_z + v_zq_y)i}$

$$$u_yj = \color{green}{(v_xq_z + v_yq_w - v_zq_x)j}$

$$$u_zk = \color{blue}{(-v_xq_y + v_yq_x + v_zq_w)k}$



Vamos a contar el resto, es decir $$$q*M$y obtener el vector deseado.



Nota. Para no sobrecargar los cálculos, presentamos solo la parte imaginaria (vector) de este producto. Después de todo, es ella quien caracteriza el vector deseado.



$$$\vec{v}' = q*M = (q_w + q_xi + q_yj + q_zk)(u_w + u_xi + u_yj + u_zk) =$

$$$= \color{red}{q_wu_xi} + \color{green}{q_wu_yj} + \color{blue}{q_wu_zk} +$

$$$+\color{red}{q_xu_wi} + \color{blue}{q_xu_yk} - \color{green}{q_xu_zj} +$

$$$+\color{green}{q_yu_wj} - \color{blue}{q_yu_xk} + \color{red}{q_yu_zi} +$

$$$+\color{blue}{q_zu_wk} +\color{green}{q_zu_xj} -\color{red}{q_zu_yi}$



Recojamos los componentes del vector.



$$$v_x' = \color{red}{q_wu_x + q_xu_w + q_yu_z - q_zu_y}$

$$$v_y' = \color{green}{q_wu_y - q_xu_z + q_yu_w + q_zu_x}$

$$$v_z' = \color{blue}{q_wu_z + q_xu_y - q_yu_x + q_zu_w}$



$$$v' = (v_x', v_y', v_z')$

Por lo tanto, se obtiene el vector requerido. Escriba el



código:

private static Vector3 QuanRotation(Vector3 v,Quaternion q)
{
        float u0 = v.x * q.x + v.y * q.y + v.z * q.z;
        float u1 = v.x * q.w - v.y * q.z + v.z * q.y;
        float u2 = v.x * q.z + v.y * q.w - v.z * q.x;
        float u3 = -v.x * q.y + v.y * q.x + v.z * q.w;
        Quaternion M = new Quaternion(u1,u2,u3,u0);
        
        Vector3 resultVector;
        resultVector.x = q.w * M.x + q.x * M.w + q.y * M.z - q.z * M.y;  
        resultVector.y = q.w * M.y - q.x * M.z + q.y * M.w + q.z * M.x;
        resultVector.z = q.w * M.z + q.x * M.y - q.y * M.x + q.z * M.w;
        
        return resultVector;
}

Acto 2. Encontrar los vértices de un cubo

Sabiendo cómo rotar un vector con un cuaternión, no será difícil encontrar todos los vértices del cubo.



Pasemos a la función de encontrar los vértices de un cubo. Definamos las variables base.

private static Vector3[] GetPoint(Box box)
{
        //    
        Vector3[] point = new Vector3[8];

        // 
        //....

        return point;
}

A continuación, debe encontrar un punto (punto de anclaje) desde el cual será más fácil encontrar otros vértices.



Reste la mitad de la dimensión del cubo del centro de coordenadas, y luego agregue una dimensión del cubo al punto de pivote.

//...
        //  
        point[0] = box.Center - box.Size/2;
        point[1] = point[0] + new Vector3(box.Size.x , 0, 0);
        point[2] = point[0] + new Vector3(0, box.Size.y, 0);
        point[3] = point[0] + new Vector3(0, 0, box.Size.z);
		
	//     
        point[4] = box.Center + box.Size / 2;
        point[5] = point[4] - new Vector3(box.Size.x, 0, 0);
        point[6] = point[4] - new Vector3(0, box.Size.y, 0);
        point[7] = point[4] - new Vector3(0, 0, box.Size.z);
//...

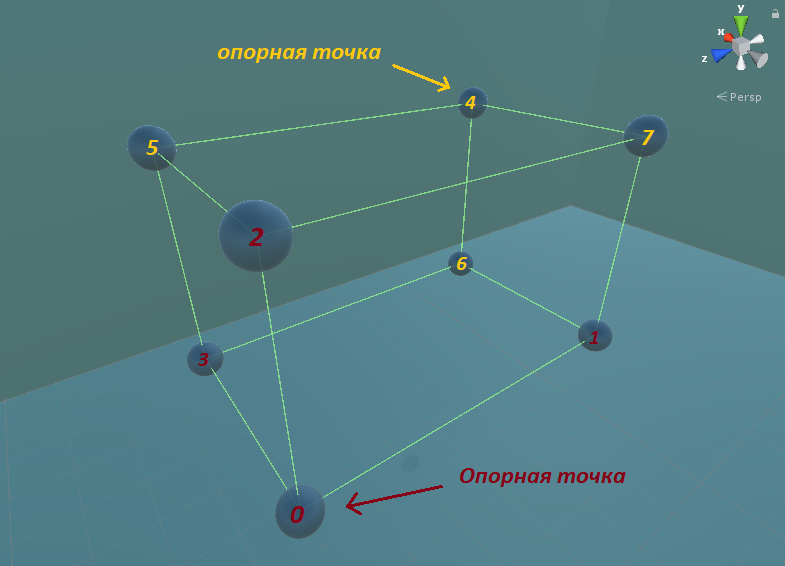
Podemos ver cómo se forman los puntos



Después de encontrar las coordenadas de los vértices, es necesario rotar cada vector por el cuaternión correspondiente.

//...

        for (int i = 0; i < 8; i++)
        {
            point[i] -= box.Center;//    

            point[i] = QuanRotation(point[i], box.Quaternion);//

            point[i] += box.Center;// 
        }

//...

Pasemos a las proyecciones.

Acto 3. Buscar ejes divisorios

El siguiente paso es encontrar el conjunto de ejes que dicen estar dividiéndose.

Recuerde que se puede encontrar en los siguientes conjuntos:

• Planos normales de cada cubo (rojo)
• Producto vectorial de los bordes de los cubos. $$$\{[\vec{x},\vec{y}[ : x∈X, y∈Y\}$donde X es los bordes del primer cubo (verde) e Y es el segundo (azul).

Para obtener los ejes necesarios, es suficiente tener cuatro vértices del cubo, que forman un sistema ortogonal de vectores. Estos vértices están en las primeras cuatro celdas de la matriz de puntos que formamos en el segundo acto.







Es necesario encontrar las normales del plano generadas por los vectores:

• $$$\vec{a}$ y $$$\vec{b}$
• $$$\vec{b}$ y $$$\vec{c}$
• $$$\vec{a}$ y $$$\vec{c}$

Para hacer esto, es necesario iterar a través de los pares de bordes del cubo para que cada nueva muestra forme un plano ortogonal a todos los planos obtenidos anteriormente. Fue increíblemente difícil para mí explicar cómo funciona, así que proporcioné dos versiones del código para ayudarlo a comprender.





Pero puedes hacerlo más fácil:

private static List<Vector3> GetAxis(Vector3[] a, Vector3[] b)
{
        //
        Vector3 A;
        Vector3 B;

	//  
        List<Vector3> Axis = new List<Vector3>();

	//   
        for (int i = 1; i < 4; i++)
        {
            A = a[i] - a[0];
            B = a[(i+1)%3+1] - a[0];
            Axis.Add(Vector3.Cross(A,B).normalized);
        }
	//  
        for (int i = 1; i < 4; i++)
        {
            A = b[i] - b[0];
            B = b[(i+1)%3+1] - b[0];
            Axis.Add(Vector3.Cross(A,B).normalized);
        }

        //...
}

También tenemos que encontrar todos los productos vectoriales de los bordes de los cubos. Esto se puede organizar mediante una simple búsqueda:

private static List<Vector3> GetAxis(Vector3[] a, Vector3[] b)
{
        //...
        // 
        //... 

       //    
        for (int i = 1; i < 4; i++)
        {
            A = a[i] - a[0];
            for (int j = 1; j < 4; j++)
            {
                B = b[j] - b[0];
                if (Vector3.Cross(A,B).magnitude != 0)
                {
                    Axis.Add(Vector3.Cross(A,B).normalized);
                }
            }
        }
        return Axis;
}

Acto 4. Proyecciones sobre el eje

Hemos llegado al punto más importante. Aquí tenemos que encontrar las proyecciones de los cubos en todos los ejes divisorios potenciales. El teorema tiene una consecuencia importante: si los objetos se cruzan, entonces el eje en el cual la intersección de la proyección de los cubos es mínima es la dirección (normal) de la colisión, y la longitud del segmento de intersección es la profundidad de penetración.



Pero primero, recuerde la fórmula para la proyección escalar del vector v sobre el vector unitario a :

$$

$$proj_\left\langle \vec{a} \right\rangle \vec{v} = \frac{(\vec{v},\vec{a})}{| \vec{a} |}$$

private static float ProjVector3(Vector3 v, Vector3 a)
{
        a = a.normalized;
        return Vector3.Dot(v, a) / a.magnitude;
        
}

Ahora describiremos una función que determinará la intersección de las proyecciones en los ejes candidatos.



La entrada son los vértices de dos cubos y una lista de posibles ejes divisorios:

private static Vector3 IntersectionOfProj(Vector3[] a, Vector3[] b, List<Vector3> Axis)
{
        for (int j = 0; j < Axis.Count; j++)
        {
           //     
           //         
        }
        //       ,   ,    
        //    .
}

La proyección en el eje se establece mediante dos puntos que tienen valores máximos y mínimos en el eje mismo: a







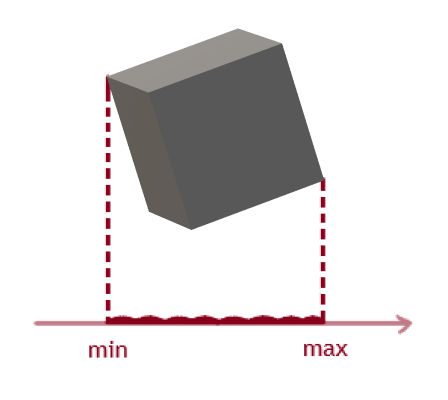
continuación, creamos una función que devuelve los puntos de proyección de cada cubo. Se necesitan dos parámetros de retorno, una matriz de vértices y un eje divisorio potencial.

private static void ProjAxis(out float min, out float max, Vector3[] points, Vector3 Axis)
{
        max = ProjVector3(points[0], Axis);
        min = ProjVector3(points[0], Axis);
        for (int i = 1; i < points.Length; i++)
        {
            float tmp = ProjVector3(points[i], Axis);
            if (tmp > max)
            {
                max = tmp;
            }

            if (tmp < min)
            {
                min= tmp;
            }
        }
}

Entonces, aplicando esta función ( ProjAxis ), obtenemos los puntos de proyección de cada cubo.

private static Vector3 IntersectionOfProj(Vector3[] a, Vector3[] b, List<Vector3> Axis)
{
        for (int j = 0; j < Axis.Count; j++)
        {
            //  a
            float max_a;
            float min_a;
            ProjAxis(out min_a,out max_a,a,Axis[j]);

            //  b
            float max_b;
            float min_b;
            ProjAxis(out min_b,out max_b,b,Axis[j]);
            
            //...
        }
        //...
}

Luego, en base a los vértices de proyección, determinamos la intersección de las proyecciones:







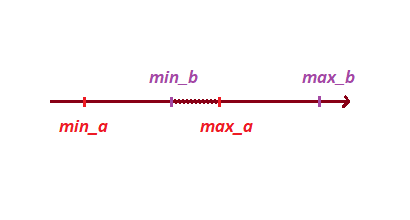
para hacer esto, pongamos nuestros puntos en una matriz y ordenemos, este método nos ayudará a determinar no solo la intersección, sino también la profundidad de la intersección.

            float[] points = {min_a, max_a, min_b, max_b};
            Array.Sort(points);

Tenga en cuenta la siguiente propiedad:



1) Si los segmentos no se cruzan , entonces la suma de los segmentos será menor que el segmento por los puntos extremos formados:







2) Si los segmentos se cruzan , entonces la suma de los segmentos será mayor que el segmento por los puntos extremos formados:







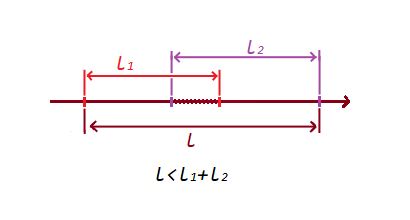
con una condición tan simple, verificamos la intersección y la no intersección segmentos



Si no hay intersección, entonces la profundidad de la intersección será cero:

            //...
            // 
            float sum = (max_b - min_b) + (max_a - min_a);
            //  
            float len = Math.Abs(p[3] - p[0]);
            
            if (sum <= len)
            {
                //  
                //  
                return Vector3.zero;
            }
            //,        
            //....

Por lo tanto, es suficiente para nosotros tener al menos un vector en el que las proyecciones de los cubos no se crucen, entonces los cubos en sí no se cruzan. Por lo tanto, cuando encontramos el eje de división, podemos omitir la comprobación de los vectores restantes y terminar el algoritmo.



En el caso de la intersección de cubos, todo es un poco más interesante: la proyección de los cubos en todos los vectores se intersectará, y debemos definir el vector con la mínima intersección.



Creemos este vector antes del bucle, y almacenaremos el vector con la longitud mínima. Por lo tanto, al final del ciclo, obtenemos el vector deseado.

private static Vector3 IntersectionOfProj(Vector3[] a, Vector3[] b, List<Vector3> Axis)
{
        Vector3 norm = new Vector3(10000,10000,10000);
        for (int j = 0; j < Axis.Count; j++)
        {
                //...
        }
        // ,      ,  
        return norm;
{

Y cada vez que encontramos el eje en el que se cruzan las proyecciones, verificamos si es el más pequeño de todos. multiplicamos dicho eje por la longitud de la intersección, y el resultado será la normal (dirección) de intersección de los cubos deseada.



También agregué una definición de la orientación de lo normal con respecto al primer cubo.

//...
if (sum <= len)
{
   //  
   //   
   return new Vector3(0,0,0);
}
//,        

//  -    2  1    
//(.       )
float dl = Math.Abs(points[2] - points[1]);
if (dl < norm.magnitude)
{
   norm = Axis[j] * dl;
   // 
   if(points[0] != min_a)
   norm = -norm;
}
//...

Conclusión

El proyecto con implementación y ejemplo se carga en GitHub, y puede verlo aquí .



Mi objetivo era compartir mi experiencia en la resolución de problemas relacionados con la determinación de las intersecciones de dos objetos convexos. Y también es accesible y comprensible contar sobre este teorema.