AES es el estándar de cifrado estadounidense. Parte IV

En esta parte IV, completamos la descripción del cifrado AES-128. Para los lectores que no están familiarizados con las partes anteriores del trabajo, explicaré que el material se presenta con fines educativos y esto impone una serie de características (detalles, ejemplos numéricos, fundamentos matemáticos, etc.) No solo pretende familiarizarse con el estándar , y el uso del material presentado para el desarrollo de algoritmos de cifrado y descifrado (en ausencia de una clave). Los autores de muchas publicaciones conocidas en línea (y fuera de línea) no se fijaron tales objetivos, lo que hace que estas publicaciones sean de poca utilidad para nuestros propósitos.



El proceso inverso de cifrado se denomina descifrado de mensajes. Para descifrar (con una clave) los textos cifrados (PCT), se crean una tabla de sustitución inversa y claves redondas, que se utilizan en orden inverso en relación con el esquema de cifrado, pero similar al proceso de cifrado.

Descifrar mensajes AES

La lista de operaciones para descifrar un mensaje sigue siendo la misma que para el cifrado. Más detalles sobre las operaciones se pueden encontrar aquí . Este es un principio bastante general de cifrados: una única implementación de hardware para cifrado y descifrado, que se proporciona mediante conjuntos de las mismas funciones para ambos procesos. Solo se cambia el texto fuente y la secuencia de envío de claves.



El proceso de descifrado de mensajes se implementa como una secuencia de transformaciones inversas (inversas) utilizadas para el cifrado, en el orden inverso de su secuencia durante el cifrado. También es obvio que las teclas redondas se usan en la secuencia apropiada: primero, la clave recibida en último lugar, luego la penúltima clave, y así sucesivamente hasta la primera tecla redonda.



Todos los nombres de transformación siguen siendo los mismos, pero tienen el prefijo Inv. Los consideraremos en la misma secuencia que antes. El cifrado AES permite dos opciones de descifrado, inversa y directa, que se analizan en detalle a continuación.

Opción de descifrado inverso

El descifrado inverso de un mensaje es un proceso natural de invertir el proceso de cifrado.



La operación AddRoundKey sigue siendo la misma (sin cambios) S + Ki para los 16 bytes del estado que cuando cifraba el mensaje, es decir. Es lo contrario de sí mismo. Esto se debe al hecho de que la lógica XOR se usa en la operación, y los bytes son representables en números binarios.

La clave de la última ronda simplemente se agrega (se resume) al mensaje cifrado.



InvSubBytes. La esencia de esta transformación no ha cambiado, es decir, cada byte del mensaje que se está convirtiendo se reemplaza por otro tomado de la tabla (S ^-1-bloque) reemplazo. Por supuesto, la tabla de sustitución es diferente aquí. El byte {x, y} se reemplaza por el byte de Inv S (x, y) de acuerdo con el mismo principio: x - fila de la tabla, y - su columna. El byte de reemplazo se recupera de la celda en la intersección de la fila (x) y la columna (y) de la tabla Inv S (x, y).



Como antes, el tamaño de la tabla es 16 × 16 = 256 bytes, cada uno de los cuales se obtiene por multiplicación y sustracción de matriz de vectores (transformación afín) del producto del vector de desplazamiento C. En los campos binarios, las operaciones de suma y resta son equivalentes, por lo que el vector C se puede agregar simplemente a producto. La tabla InvSubBytes se muestra a continuación. El nodo especificado de sustituciones S ^-1 se presenta en la siguiente tabla 1, los valores se dan en formato hexadecimal:



Tabla 1. Tabla de sustituciones del bloque S ^-1 inverso







La tabla muestra ejemplos de reemplazos de dos bytes 4A → 5C y 9F → 6E llenos de verde.



InvShiftRows. Esta transformación desplaza las filas de la tabla (el cuadrado del Estado) a la derecha (en la dirección opuesta al desplazamiento original). El valor del valor de desplazamiento para cada fila permanece igual: la primera fila (superior) no se desplaza por c0 = 0, la segunda se desplaza por c1 = 1, la siguiente se desplaza por c2 = 2 y la última se desplaza por c3 = 3 posiciones (celdas). Los valores c0, c1, c2, c3 se dieron en la tabla y en la figura anterior para la primera ronda de conversión de mensajes.







El resultado de dicha multiplicación en la representación escalar es:



S'0C = ({0l} · S0C) ⊕ ({0b} · S1C) ⊕ ({0d} · S2C) ⊕ ({09} · S3C);

S'1C = ({09} S0C) ⊕ ({0l} S1C) ⊕ ({0b} S2C) ⊕ ({0d} S3C);

S'2C = ({0d} S0C) ⊕ ({09} S1C) ⊕ ({0l} S2C) ⊕ ({0b} S3C);

S'3C = ({0b} S0C) ⊕ ({0d} S1C) ⊕ ({09} S2C) ⊕ ({0l} S3C).





Para obtener TI de las PC, el algoritmo de descifrado usa los mismos valores de parámetros que se usaron en el proceso de cifrado. Para la formación de la clave expandida, las reglas siguen siendo las mismas.

Opción de descifrado directo

Las peculiaridades del algoritmo de descifrado para algunas transformaciones inversas permiten preservar la misma secuencia de operaciones que en el algoritmo de cifrado, pero algunos de los valores de los parámetros requieren cambios. En primer lugar, estamos hablando de la clave (su despliegue).



La investigación ha demostrado que el orden de las funciones SubBytes () y ShiftRows () no cambia el valor del resultado, es decir, estas funciones son permutables (conmutan). Esta posición (propiedad) también es verdadera para las funciones InvSubBytes (), InvShiftRows (). Este patrón es fácil de explicar. El punto es que ambas funciones operan en bytes enteros, y los cambios son realizados por un múltiplo entero de un byte, y no cambian el valor de los bytes mismos.

Tenga en cuenta lo siguiente sobre la operación MixColumns (). Es lineal a los bytes de entrada (datos).



InvMixColumns (State XOR Round Key) = InvMixColumns (State) XOR

InvMixColumns (Round Key).

Estas características de las funciones (propiedades) permiten cambiar el orden de su aplicación, es decir,

InvSubBytes (InvShiftRows ()) = InvShiftRows (InvSubBytes ()).

AddRoundKey (InvMixColumns ()) = InvMixColumns (AddRoundKey ()),

pero siempre que las columnas (palabras de 32 bits) de la clave de descifrado expandida hayan pasado previamente a través de la función

InvMixColumns ().



Lo anterior significa que la forma de descifrado de la PC puede hacerse efectiva al preservar el orden de uso de las funciones adoptadas para el cifrado. Obviamente, en este caso, los costos de implementación de hardware y software del cifrado se reducen significativamente. Los cambios se refieren solo al procedimiento para generar la implementación clave.



En la función InvMixColumns (), debe convertir el tipo de la variable, el parámetro de entrada de la función es una matriz de bytes bidimensional (cuadrado) y la clave expandida se forma como una matriz lineal (cadena) de palabras de 32 bits. Por este motivo, es necesario realizar una coincidencia de tipos con el cuadrado.



Demostremos, usando el ejemplo de una transformación de 2 rondas, dos versiones equivalentes del procedimiento de descifrado RIJNDAEL. La primera opción es el inverso habitual de la función de cifrado. La segunda opción se obtiene de la primera cambiando el orden de las operaciones en tres pares de transformaciones

InvShi ftRows () → InvSubBytes () 2 veces y

AddRoundKey () → InvMixColumns () 1 veces.



El resultado de la transformación se guarda al pasar de la

secuencia de operaciones original a la inversa en los pares especificados.



En la tabla vemos que el procedimiento de cifrado y la segunda variante del procedimiento de descifrado coinciden con el orden de usar teclas redondas (al realizar operaciones AddRoundKey), tablas de reemplazo (al realizar operaciones SubBytes () e InvSubBytes ()) y matrices de transformación (al realizar MixColumns ( ) e InvMixColumns ()).



Tabla 2 - Secuencia de transformaciones en la versión de dos rondas de RIJNDAEL







Un resultado similar resulta ser cierto para cualquier cantidad de rondas.

Recuperación de una clave de cifrado con la última subclave

Generación de claves de cifrado redondas AES. La programación de claves para generar claves redondas a partir de una clave de cifrado original de 128 bits es una función recursiva. Esta función se discute en detalle aquí . Las condiciones iniciales para su lanzamiento son las primeras 4 palabras de 4 bytes de la clave (palabras de 4 × 32 bits), es decir, W [0], W [1], W [2], W [3]. Formulemos el problema de recuperar esta clave de cifrado de 128 bits de la siguiente manera:



deje que se encuentren los componentes de la clave redonda de 10 W [43], W [42], W [41], W [40].

Es necesario recuperar la clave de cifrado completa solo con esta clave redonda.

Es conveniente considerar primero la solución del problema en los datos numéricos. Tomemos como ejemplo el ejemplo numérico dado en FIPS PUB 197 .... La Tabla 3 contiene la clave de la ronda 10.



El procedimiento para generar claves redondas está organizado de tal manera que proporciona movimiento hacia adelante (despliegue de la clave) a lo largo de una serie de valores de clave anteriores. Para retroceder desde algún punto de una serie de valores, es necesario tener los datos iniciales del proceso de cálculo en este punto de retorno. Deje que el punto de retorno sea el último paso de la última décima ronda, es decir, se conocen cuatro palabras de 4 bytes de la clave de la décima ronda Nk = Nb = 4.



Tabla 3 - Clave de 128 bits de la décima ronda del cifrado AES







Además, los resultados y las acciones del algoritmo de recuperación de claves se colocan para conveniencia en la tabla 4, que es similar a una tabla de generación de claves (tipo de volcado).



Tabla 4 - Recuperación de la clave de cifrado de la clave conocida de la décima ronda







Explicaciones para la Tabla 4. Los números redondos se cuentan en orden inverso del 10 al 1. Tres columnas (3, 8, 9) de la tabla contienen claves preparadas con diferentes números actuales dependiendo del número de línea i. Las celdas restantes contienen datos auxiliares para cálculos intermedios. Por lo tanto, el valor de la clave W [i] aparece en la tabla tres veces en tres columnas.



Las columnas 1 y 2 son el número r de la ronda y el número ordinal i de la palabra clave de 4 bytes. La última palabra de este tipo durante el cifrado tiene el número i = 43. En la tabla la escribimos en la línea superior de la columna derecha (9). Los números i de las filas de la tabla están disminuyendo y en la columna 9 corresponden a las palabras de la tecla W [i]. La octava columna contiene la palabra W [i - Nk] de la tecla con un número reducido W [43 - 4] = W [39], y la tercera columna - la palabra clave W [i - 1] = W [42], anterior W [i] = W [43].



Se desconoce el significado de la palabra W [39] en la octava columna y lo encontramos a partir de los datos iniciales usando la fórmula:







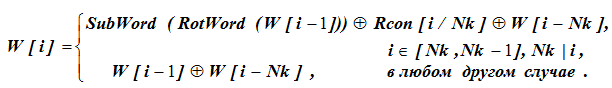
Para los cálculos de fórmula, primero se verifican las condiciones para seleccionar la línea de fórmula. Para W [43], i = 43 y Nk no divide completamente el valor 43, es decir, para i = 43 el valor de W [i] está determinado por la línea inferior de la fórmula: W [43] = W [42] W [39]. Aquí, para los valores dados de W [42] y W [43], el último término W [39] no está definido.

Entonces W [39] = W [43] W [42] = b6630ca6 - e13f0cc8.



En aritmética binaria mod2, las operaciones de suma y resta son equivalentes, por lo tanto, los cálculos en bits para cada uno de los 4 bytes de la palabra clave W [39] toman la forma (Tabla 5):

Tabla 5 - Cálculos de bytes de la palabra clave W [39].







Por lo tanto, se encontró el valor de la palabra clave W [39] = 575c006e. Transferimos este valor a la tercera columna, a la fila i = 40 y a la novena columna a la



fila i = 39. Los cálculos en la fila i = 40 se realizan como cuando se expande la clave.



La palabra desconocida W [i - Nk] = W [40 –Nk] = W [i = 36] debe determinarse como en el caso anterior por la diferencia W [36] = W [40] 7 columna de la línea 40.



A su vez, el valor en 7- La columna th de la línea 40 se forma como la suma (OR) de las columnas quinta y sexta. El valor de la quinta columna se obtiene de W [39] después de un cambio cíclico RotWord (cuarta columna) y una operación de reemplazo de SubWord (quinta columna).



Los resultados de estas acciones toman la forma

RotWord (575c006e) = 5c006e57; SubWord (5c006e57) = 4a639f5b.



El valor en la sexta columna se obtiene como una constante

Rcon [j = i / Nk] = Rcon [j = 40/4] = 2 ^j-1 = 2 ⁹ .



Esta constante está representada por un byte hexadecimal

2 ⁹ ≈100000000 = x ⁹ , pero no existe tal byte en el campo GF (2 ⁸ ): es necesario encontrar el resto de la división por un polinomio irreducible, es decir.

$$ Después de incluir la constante en la palabra clave, tenemos Rcon [j = 40 / Nk] = 36000000 (6 th columna). El valor de la 7ma columna se obtiene como (7ma columna) = (5ta columna) ⊕ (6ta columna) = 4a639f5b⊕36000000 = 7c639f5b. Y finalmente, para W [36] = W [40] (séptima columna de la fila 40) = d014f9a8 7c639f5b = ac7766f3.$^9 : ^8+ ^4+ ^3+ + 1= ^5+ ^4+ ^2+ = 00110110 = 36.$















Otros cálculos por analogía conducen al resultado final: la clave de cifrado.

Hay más información sobre w y las funciones RotWord, Rcon y SubWord. Supongamos que denotamos por Kr [j] - el byte j-ésimo de la r-ésima tecla redonda y w [i] como en la documentación.



Obtenemos: Kr = (w [Nk ∙ r], w [Nk ∙ r + 1], · · ·, w [Nk ∙ r + Nk - 1]).



Para diferentes i tenemos las siguientes relaciones



para i ≠ 0 mod Nk, Nk ≤ i <Nb ∙ (Nr +1), w [i] = w [i - Nk] xor w [i - 1] y

para i = 0 mod Nk , w [i] = w [i - Nk] xor SubWord (RotWord (w [i - 1])) xorRcon [i / Nk].



Por lo tanto, para i ≠ 0modNk, Nk 0≤i <Nb ∙ (Nr + 1) –Nk, w [i] = w [i + Nk] xor w [i + Nk - 1] y para i = 0modNk, w [i] = w [i + Nk] xorSubWord (RotWord (w [i + Nk - 1])) xorRcon [i + Nk / Nk]

Con AES-256, debe agregar una operación Subword cuando i es comparable a 4mod Nk. Por lo tanto, es posible deducir la clave anterior de la subclave final y obtener paso a paso el valor K0 de la clave de cifrado.



Los fundamentos matemáticos del cifrado AES - 128 son bastante completos y detallados aquí .



Pasemos al mapeo de campo ℓ: GF (2 ⁸ ) → GF (2 ⁸ ); x → x ² + x. La imagen de este mapeo

1 = Im (l) tiene dimensión dim GF (2) (1) = 7.



Ecuación x ² + x = θ, donde θ 1 tiene dos soluciones diferentes (la raíz de la ecuación) 1, 2є GF (2 ⁸ ).



Por el teorema Wyeth h1⊕h2 = 1, la suma de las raíces es igual al coeficiente de la ecuación para x ²con el signo opuesto, y el producto de las raíces x1⊗x2 = θ es igual al término libre de la ecuación (en nuestra ecuación con el signo opuesto).



Se sabe que en la aritmética de los campos binarios, las operaciones de suma y resta de elementos mod2 son equivalentes.







Por lo tanto, las raíces de la ecuación están relacionadas por la relación x2 = x1⊕1, ya que el coeficiente en x en la ecuación es 1. Esto significa que en la representación decimal de los elementos de campo en su ordenamiento lexicográfico, se ubican uno después del otro, difiriendo solo en uno.



Entonces para x = 0 y x = 1 y para x = 2 y x = 3 obtenemos:







Los resultados (imágenes) del mapeo en los pares reducidos (0, 1); (2, 3) coincidió completamente, es decir Dos tipos corresponden a una imagen. En consecuencia, la cardinalidad de la imagen es dos veces menor que la cardinalidad de la preimagen y su dimensión de sus elementos es 7.



El producto de pares de raíces, es decir, el término libre de una ecuación cuadrática se define convenientemente a través de la representación de potencia de los elementos del campo (imágenes inversas). En este caso, los exponentes se resumen mod255, es decir módulo el orden del grupo multiplicativo del campo GF (2 ⁸ ).