¿Qué es la música en términos matemáticos? ¿Qué es "la" o "mi"? En la guitarra se comprende bien cómo se forman exactamente los sonidos.
Sonido "mi" (sonido libre de la 1ª cuerda), sonido "la" ( 1ª cuerda sujeta al 5º traste ). "La" es 440 Hz. ¿Qué significa 440 Hz? Eso es 440 veces la cuerda vibra por segundo. El sonido "mi" es 5 semitonos más bajo que el sonido "la" ( sujeto en el quinto traste ).

Otros 7 semitonos más abajo, obtendré "mi" de nuevo, es decir. octava. ¿Por qué tanto el sonido libre de la primera cuerda como el sonido de la cuerda sujeta en el traste 12 se llaman la misma palabra "mi"?

Nos parece que se toca la misma nota. El hecho es que la longitud de la cuerda en este punto ( "mi" en el traste 12 ) se divide exactamente por la mitad:
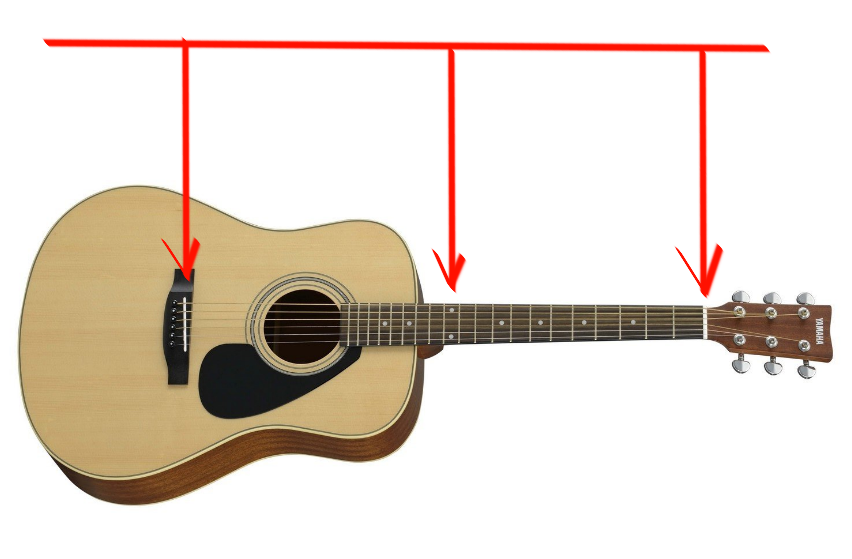
esto significa que las vibraciones de este resto de la cuerda, según las leyes de la física, serán dos veces más frecuentes que las vibraciones de una cuerda completa.
Cada vez que bajo la cuerda y la aprieto en el siguiente traste (la división indicada por la línea perpendicular en el diapasón ), el sonido sube un semitono, como dicen los músicos.
Tenga en cuenta que los trastes en el diapasón son de diferentes anchos. Se reducen gradualmente, porque para aumentar la frecuencia en un semitono, debe reducir la longitud de la cuerda en un cierto número de veces.
¿Qué estoy insinuando al enfocarme en el hecho de que algo "en" se traduce en algo "en"? Los matemáticos dirían que solo hay una función (en algunas condiciones) donde + va ax ( multiplicar ). Y esta función se llama logaritmo.
Esto significa que nuestros oídos, al acortar la cuerda y elevar el sonido un cierto número de veces, se perciben como subiendo un semitono. Es decir, cada traste acorta la cuerda el mismo número de veces, y nuestros oídos dicen que subimos un semitono, alcanzando la nota "E" y recibiendo una octava. Nuestros órganos auditivos son logarítmicos.
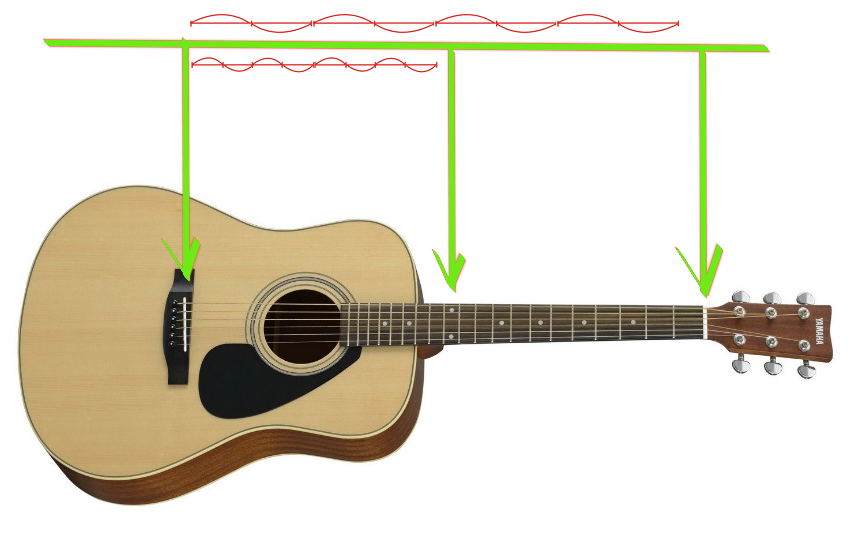
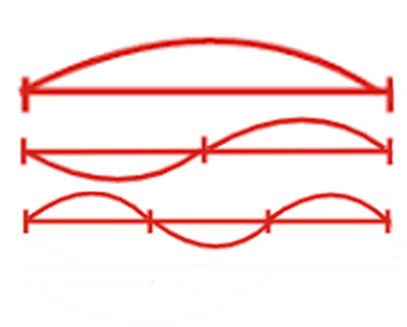
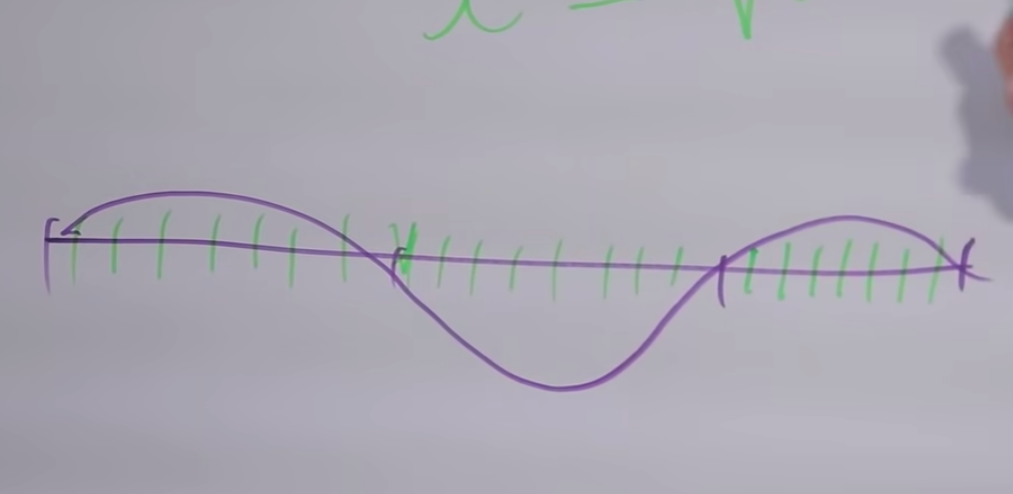
Decimos que "mi" y "mi" son dos veces diferentes, esto se puede ver en el sonido. El arco superior está en pleno movimiento. Cuando lo sujetamos en el medio, la cuerda comienza a vibrar, como en el gráfico del medio.
¿Por qué los sonidos son similares? El hecho es que junto con la vibración principal de la cuerda, de hecho, la vibración de la misma cuerda ocurre en todas las frecuencias, donde la longitud de la sección vibratoria es inversamente proporcional a la frecuencia.
En consecuencia, si la longitud disminuye en un número entero de veces, entonces se puede escuchar el sobretono correspondiente. El sobretono correspondiente se realiza mediante la cuerda dada. Si una cuerda determinada vibra parcialmente fija en estos dos puntos ( gráfico inferior ), entonces su tono será tres veces más alto.
El oído percibe un doble aumento de frecuencia como la misma nota. Todos los matices que dividimos varias veces, es decir cualquier división de medio segmento es tanto una división automática como un segmento grande. Y solo algunas divisiones de un segmento grande no encajan en el esquema de media división.
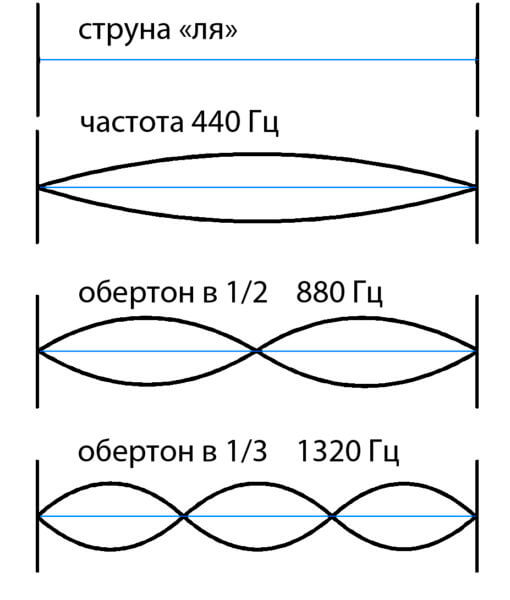
Si tomamos los sonidos superiores pares para una cuerda larga, entonces serán los sonidos superiores para una cuerda medio acortada. Y absolutamente cualquier sonido acortado de una cuerda corta sonará para una larga. Por tanto, sentimos que todo lo que escuchamos coincide en estos puntos, y lo percibimos como una nota.
Más interesante aún es que hay notas que pasan por varios semitonos, y nuestros oídos las perciben como una consonancia, un acorde, algo agradable al oído, que no corta nuestros oídos. ¿Qué son estas notas?
Si toma 7 semitonos, tome la nota "A" y suba el sonido en 7 semitonos, hasta la siguiente "E", entonces esas dos notas sonarán bien.
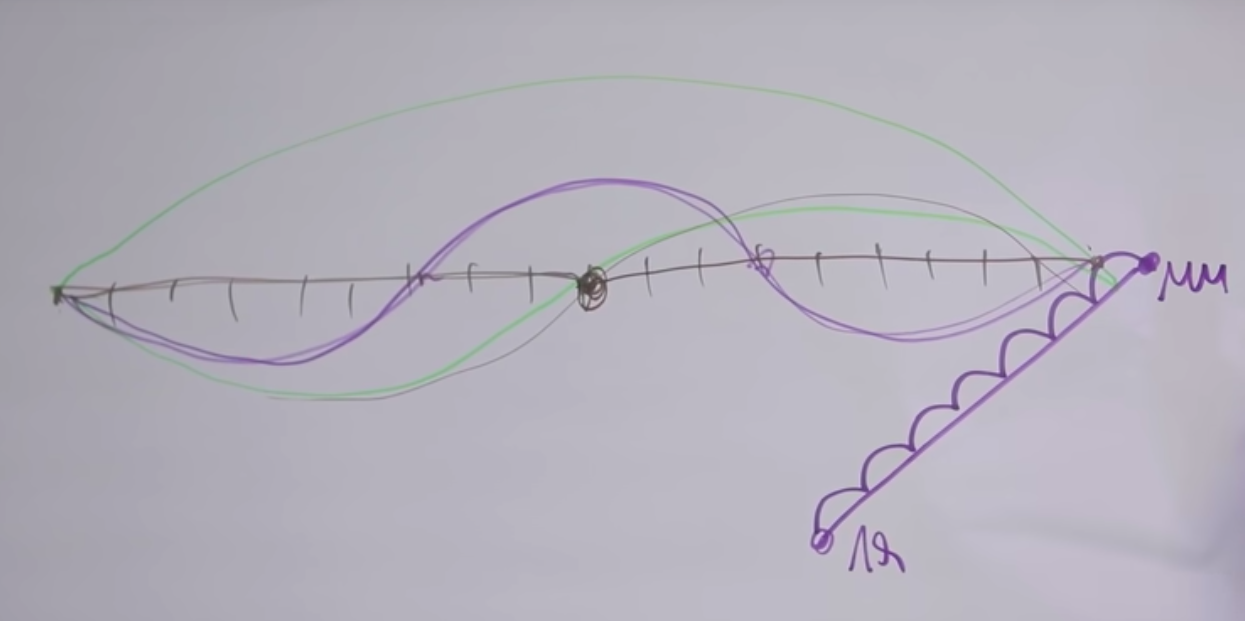
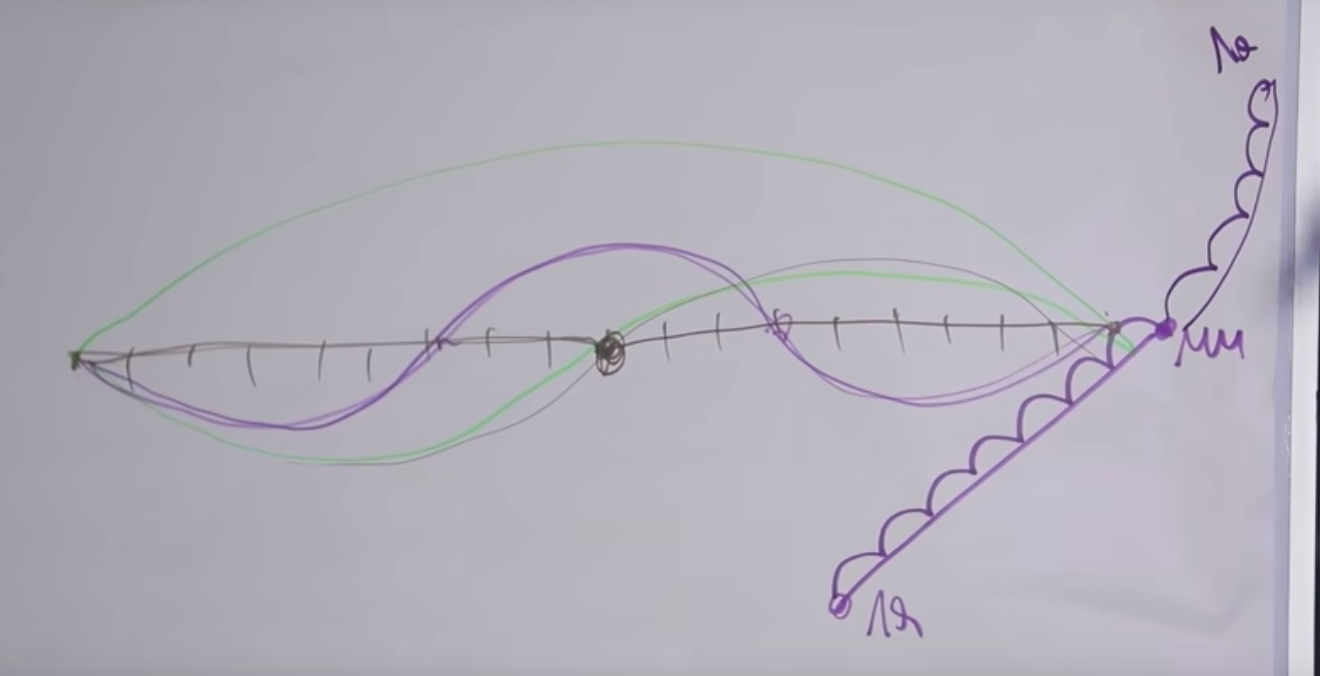
Si retrocede otros 5 semitonos hacia arriba, habrá una "la" más alta de la siguiente octava. Por alguna razón, este intervalo también nos suena agradable. Vamos a resolverlo todo.
En primer lugar, si un aumento de 1 semitono es un aumento de la frecuencia de las oscilaciones en un cierto número de veces, lo designaremos como x. Si necesita subir un semitono más, entonces ya habrá x * x, es decir, x 2 . Si lo subí 12 semitonos (x 12 ), entonces debería subir exactamente 2 veces. Obtenemos la ecuación x 12 = 2.
Por lo tanto, un aumento de 1 semitono significa una contracción de la cuerda en x = 12√2, o lo que es lo mismo, elevar la frecuencia del sonido en 12 √2.
¿Y qué tienen que ver "la" y "mi" con eso? ¿Por qué 7 semitonos suenan melódicos? Subamos el grado:
¿Qué es tan agradable, bueno en este número?
En algún momento de la antigüedad, se inventaron los clavidores templados, una grabación precisa de la música. Lo puedes ver muy bien en la guitarra, también lo puedes encontrar en el piano, está escondido adentro, si miras adentro, puedes ver las cuerdas.
Ahora, este número está muy cerca de 3/2. Si calcula con una calculadora, será muy preciso. Esto significa que "mi" es aproximadamente 1,5 veces mayor que la "la" anterior. Aquellos. levantar 7 tonos equivale a subir 3/2 veces, lo que significa que tenemos muchos matices superiores iguales.
Porque cualquier división por un número entero de un segmento pequeño será una división entera de todo el segmento. Y, en consecuencia, dividir el corte original por el número de piezas, un múltiplo de tres, será la división del segmento pequeño (⅓), y también ⅔. Cuando dejamos ⅔ de la longitud, es decir subimos la frecuencia a 3/2, subimos unos 7 semitonos, tendremos muchos armónicos comunes, será una consonancia agradable.
Los 4/3 restantes son exactamente los 5 semitonos restantes, 3/2 x 4/3 = 2, solo una octava. Que corresponde a la fórmula x71243. El valor está muy cerca de 4/3, pero no del 100%. Este número es irracional, no se puede escribir como una fracción, no se puede escribir como un número entero dividido por un número entero.
Escuché que hay un instrumento en la India ( sitar), en el que la octava se divide en 19 partes, es decir tienen un semitono = 1/19 octava, 19x2.

Y ya con gran precisión x121932, lo que significa que si en un instrumento indio así retrocede 12 de 19 segmentos, entonces en esta consonancia habrá más matices coincidentes, y este intervalo suena como un bálsamo para los oídos.
Hay muchas cosas interesantes que decir sobre música y matemáticas. En particular, se percibe un acorde mayor si se agregan 4 semitonos a cualquier nota inicial, y luego 3, es decir, 0 - 4 - 3. Un menor, si suma 3 al principio, y luego 4, es decir 0 - 3 - 4. La primera y la última de las tres notas del acorde será "la misma", solo difiere en 7 semitonos, pero el sonido del medio creará nuestra percepción de consonancia y afinará en un modo menor o mayor.
Parecería que la música y las matemáticas, ¿qué pueden tener en común? Y hay tanto en común que los matemáticos y los músicos a menudo se comunican, además, los matemáticos entienden fácilmente a los músicos, por así decirlo, captan un semitono.
Varios enlaces útiles: