¡Hola habitantes! Un coloso con pies de arcilla es lo que podríamos llamar un programador sin experiencia en Ciencias de la Computación. El dominio seguro de los conceptos básicos le permite no "reinventar la rueda" y crear soluciones efectivas en la arquitectura del software. Todo esto elimina errores y costos excesivos de prueba y refactorización.
No importa si se siente fuera de lugar cuando otros programadores están discutiendo el límite aproximado. Incluso los expertos con experiencia cometen errores porque se han olvidado de la informática.
Por qué se necesita este libro
Muchos de mis compañeros desarrolladores (del autor) llegaron a la profesión desde una amplia variedad de campos. Algunos tienen educación superior en Ciencias de la Computación; otros estudiaron fotografía, matemáticas o ni siquiera se graduaron de la universidad.
En los últimos años, he notado que los programadores están cada vez más ansiosos por aprender Ciencias de la Computación por varias razones:
- convertirse en buenos programadores;
- para responder preguntas sobre algoritmos durante las entrevistas;
- para satisfacer su curiosidad en el campo de la Informática, o finalmente para dejar de lamentar que en un momento no tuvieron la oportunidad de dominar esta asignatura.
Este libro es para todos ustedes.
Muchos encontrarán aquí temas que son interesantes por derecho propio. Traté de mostrar en qué situaciones reales (no académicas) este conocimiento será útil. Después de leer este libro, quiero que adquieras los mismos conocimientos que después de estudiar el curso básico de Ciencias de la Computación y que también aprendas a aplicarlo.
En pocas palabras, el propósito de este libro es ayudarlo a convertirse en un programador más capacitado y experimentado a través de una mejor comprensión de la informática. No puedo encajar 20 años de enseñanza universitaria y experiencia profesional en un libro ... pero intentaré hacer lo mejor que pueda. Espero que encuentre al menos un tema aquí, sobre el que pueda decir: "Sí, ahora lo entiendo", y aplique el conocimiento en su trabajo.
Lo que no encontrarás en la edición
El significado del libro es ayudar al lector a comprender mejor las Ciencias de la Computación y aplicar los conocimientos en la práctica, y no reemplazar completamente cuatro años de estudio.
En particular, este no es un libro de prueba. De hecho, en el segundo volumen del libro , se consideran los métodos de prueba, pero los algoritmos estándar generalmente se presentan aquí sin pruebas. La idea es que el lector conozca la existencia de estos algoritmos y aprenda a utilizarlos sin entrar en detalles. Como libro de prueba escrito para estudiantes de pregrado y posgrado, recomiendo encarecidamente Introducción a los algoritmos de Cormen, Leiserson, Rivest y Stein (los autores suelen agruparse en abreviatura CLRS).
Este tampoco es un libro de programación: no encontrará pautas sobre cuándo usar int y cuándo usar double, o una explicación de qué es un bucle. Se espera que el lector pueda comprender los listados de pseudocódigo que se utilizan para describir los algoritmos (todos los programas de este libro están escritos en pseudocódigo basado en el lenguaje C). El propósito del libro es conectar los conceptos de Ciencias de la Computación con técnicas de programación ya familiares para el lector.
10. Programación dinámica
10.1. Problema de campos faltantes
Supongamos que tenemos un tablero de ajedrez n × n al que le faltan varios cuadrados. ¿Cómo encontrar la pieza k × k más grande de un tablero sin campos faltantes?
Si no ha enfrentado un problema de este tipo antes, tómese unos minutos para escribir una solución y determinar el tiempo de ejecución de su algoritmo.
Ante este problema, razoné de la siguiente manera. Cada campo de tablero de ajedrez puede pertenecer a muchas de las áreas más grandes, pero solo en una de ellas puede ser la esquina superior izquierda. Si marco cada casilla con el tamaño del área intacta más grande de la que es la esquina superior izquierda, entonces el campo con la marca más grande corresponderá al área deseada.
Suponga que el tablero se representa como una matriz n × n, en la que cada celda contiene 1 si el campo correspondiente está presente y 0 si falta. Si el valor actual de la celda es 0, el campo correspondiente está ausente y no puede ser parte de una región contigua, por lo que no es necesario cambiarlo. Si el valor es 1, entonces podemos reemplazarlo con un número que sea uno más que el valor mínimo de las tres celdas ubicadas debajo y a la derecha.
Cambiamos cada celda de la matriz una vez, lo que incluye verificar si el valor de la celda es cero, verificar los valores de hasta tres celdas más y escribir el nuevo valor de celda. Cada una de estas operaciones toma O (1) tiempo, por lo que el tiempo que toma procesar todo el tablero de ajedrez es
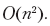
Tenga en cuenta que este es un tiempo de ejecución lineal, no cuadrático, para el algoritmo - en un tablero de ajedrez n (asumimos que n es el número total de campos, y nos adherimos a la convención habitual de que n es la cantidad de datos de entrada) campos (algunos de ellos son ausente), por lo que el tiempo total empleado por el algoritmo es proporcional al número de campos. Si denotamos con mayor precisión el tamaño del tablero de ajedrez como √ n × √ n, entonces obtenemos n campos y el tiempo total de ejecución es O (n).
10.2. Trabajar con subtareas superpuestas
El enfoque utilizado en esta sección se llama programación dinámica. Se utiliza cuando un problema se puede dividir en varias subtareas, la solución de cada una de las cuales se utilizará varias veces. Este enfoque se diferencia del principio de "divide y vencerás", cuando el problema se divide en subtareas, que se resuelven independientemente unas de otras. En el problema del tablero de ajedrez, cada subproblema dependía de las soluciones a otros tres problemas, y las soluciones a todos los subproblemas se guardaban para su uso posterior.
La programación dinámica generalmente se realiza construyendo tablas como se muestra arriba. Esto significa resolver un problema utilizando un enfoque de abajo hacia arriba, donde comenzamos resolviendo los subproblemas más pequeños y avanzamos hasta llegar a una respuesta. Otro método es la memorización, donde vamos de arriba a abajo, resolviendo subproblemas según sea necesario y almacenando en caché los resultados para su reutilización. Construir tablas es la opción preferida cuando necesitas resolver cada subproblema (en mi ejemplo con un tablero de ajedrez, era necesario encontrar el área intacta más grande para cada campo del tablero), ya que los costos de este método son menores que con la memorización. Si no es necesario resolver algunas subtareas del área de soluciones, la memorización le permite resolver solo aquellas subtareas que son realmente necesarias.
El punto clave
Donde dividir y conquistar implica dividir una tarea en varias subtareas independientes, la programación dinámica significa dividir una tarea en varias subtareas superpuestas. La solución a cada subproblema se almacena en caché para su posterior reutilización.
10.3. Programación dinámica y caminos más cortos
Considere el problema de encontrar la ruta más corta: para un gráfico dado con bordes ponderados, necesita encontrar una ruta de un nodo a otro que tenga el costo más bajo.
Definición Un
gráfico ponderado por bordes es un gráfico en el que cada borde tiene su propio peso (costo). El costo de una ruta de un nodo a otro está determinado por la suma del costo de todos los bordes atravesados.
Suponga que encontramos una ruta entre los nodos syt que contiene el tercer nodo v. Entonces, la ruta de sa t debe contener la ruta más corta de sa v, porque de lo contrario podríamos reemplazar este segmento con una ruta más corta y reducir la longitud de la ruta más corta de sa t, lo que contradice la condición inicial (este es el principio de optimalidad de Bellman).
( ) , . , . , .
, , .
Los problemas de encontrar el camino más corto son ejemplos sorprendentes de programación dinámica, ya que la propiedad óptima de una subestructura es intuitivamente clara: es obvio que la forma más rápida de ir del punto A al punto C a través del punto B es también la forma más rápida de ir del punto A al punto B y del punto B al punto C. El número de algoritmos basados en este principio incluye el método Bellman-Ford, que encuentra el camino más corto desde el punto de partida a cualquier vértice del gráfico (o desde cualquier vértice del gráfico al punto final) y el método Floyd-Warshall, con su ayuda Se calcula la ruta más corta entre cada par de vértices del gráfico. En ambos casos, la idea es comenzar con un pequeño subconjunto de nodos cerca de los nodos de interés y expandir gradualmente ese conjunto utilizando los nodos ya encontrados para calcular nuevas distancias.
10.4.
10.4.1. Git merge
Otra tarea que se usa comúnmente para demostrar la programación dinámica es encontrar la subsecuencia común más larga. La tarea es encontrar, para dos cadenas A y B dadas, la secuencia más larga que ocurre en ambas cadenas, manteniendo la secuencia de caracteres. Las cadenas no tienen que estar en una fila; por ejemplo, si A = {acdbef} y B = {babdef}, entonces {adef} será su subsecuencia común.
Al fusionar cambios en Git (fusionar), busca la subsecuencia común más grande entre las ramas maestra y de trabajo. Los caracteres presentes en el maestro pero no presentes en la subsecuencia común más grande se eliminan; los caracteres que están en la rama de trabajo pero que no están en esta subsecuencia se agregan al maestro.
10.4.2. LATEX
El sistema de preparación de documentos LATEX se utiliza a menudo para crear documentos técnicos. Una de las tareas del sistema de mecanografía es alinear el texto a derecha e izquierda al mismo tiempo; para hacer esto, los espacios entre palabras y caracteres se alargan o encogen para que todas las líneas tengan la misma longitud. Otra forma de alinear el texto es ajustar la última palabra para que parte de la palabra aparezca en la siguiente línea. LATEX (Desde un punto de vista técnico, casi todo el trabajo lo hace el sistema de entrada de texto TEX; LATEX está construido sobre TEX. Aquí utilizo LATEX por razones de simplicidad) intenta encontrar puntos de salto de línea óptimos para que el texto se vea bien. Si esto falla, varias líneas seguidas terminarán con un guión de palabras o la distancia entre palabras en diferentes líneas será diferente.LATEX tiene un conjunto de reglas para evaluar el "fallo" de la alineación. El programa busca encontrar la opción "menos mala".
Si hay n posibles puntos de salto de línea en un párrafo, existen
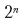posibles opciones para dividir el texto. El "fallo" de la selección para cada punto de ruptura depende de qué puntos de ruptura se seleccionaron antes. Por lo tanto, volvemos a tener subtareas superpuestas. El uso de técnicas de programación dinámica reduce el tiempo de ejecución al 
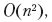que se puede mejorar con métodos adicionales.
»Más detalles sobre el libro se pueden encontrar en el sitio web de la editorial
» Tabla de contenido
» Extracto
para los habitantes un 25% de descuento en el cupón - Ciencias de la computación
Al pagar la versión impresa del libro, se envía un libro electrónico por correo electrónico.