¿Cuál es el futuro de las matemáticas?
- En la década de 1990, las computadoras comenzaron a jugar al ajedrez mejor que los humanos.
- En 2018, las computadoras juegan mejor al Go que los humanos.
- En 2019, el investigador de inteligencia artificial Christian Szegedy me dijo que dentro de 10 años, las computadoras serán mejores para probar teoremas que los humanos.
Por supuesto, puede estar equivocado. O tal vez tenga razón.
Creo en esto: dentro de diez años, las computadoras nos ayudarán a probar teoremas tristes al nivel de los primeros estudiantes de posgrado. ¿Qué áreas de las matemáticas? Depende de quién se involucre en esta área de investigación.
El patrón típico de la inteligencia artificial es el siguiente: al principio es muy estúpido y luego de repente se vuelve más inteligente. La pregunta natural es: ¿cuándo ocurre la transición de fase y la inteligencia artificial de repente se vuelve muy inteligente? Respuesta: nadie sabe esto. Lo que está claro es que cuantas más personas se involucren en esta área de investigación, antes sucederá.
¿Qué es prueba?
Si le pregunta a un excelente estudiante, un investigador matemático y una computadora qué es la prueba, ¿cuál es su respuesta? Las respuestas del alumno sobresaliente y la computadora coincidirán y serán las siguientes:
— , , , , , , .Por supuesto, la respuesta de un matemático investigador no sería tan idealista. Para un matemático, la definición de prueba es lo que otros matemáticos experimentados consideran prueba. O lo que se acepta para publicación en Annals of Mathematics o Inventiones.
Sin embargo, hay un pequeño problema con esto. Las siguientes capturas de pantalla son de Annals of Mathematics , una de las revistas matemáticas más prestigiosas del mundo.
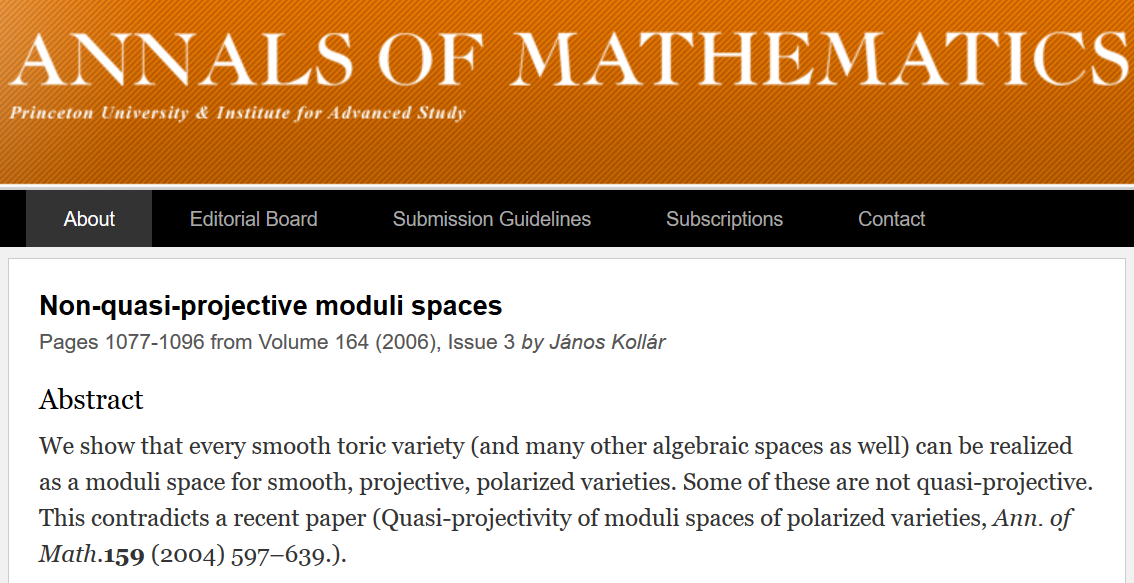
El segundo artículo contradice literalmente al primero. Los autores escriben abiertamente sobre esto en la anotación. Hasta donde yo sé, Annals of Mathematics nunca ha publicado una refutación a ninguno de estos trabajos. ¿Qué trabajo es considerado correcto por matemáticos experimentados? Solo puede averiguarlo si trabaja en este campo.
Salida: en las matemáticas modernas, la opinión sobre si algo es prueba cambia con el tiempo (por ejemplo, puede pasar de “es” a “no es”).
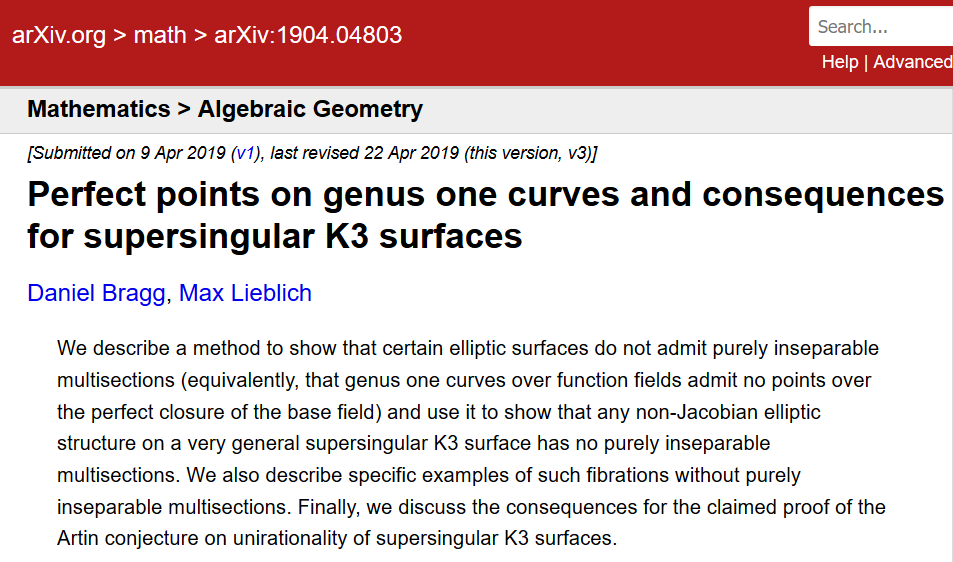
Este breve artículo de 2019 señala que otro artículo importante de 2015 publicado en Inventiones se basa en gran medida en un lema falso. Esto no se notó hasta 2019, a pesar de que en 2016 se realizaron talleres para estudiar esta importante obra.
Vladimir Voevodsky, ganador del Premio Fields que contribuyó a los fundamentos de las matemáticas, escribe que “si un autor en el que la gente confía escribe un argumento técnicamente complejo que es difícil de verificar, pero que es similar a otros argumentos correctos, entonces este argumento casi nunca se todo se comprobará en detalle ".
Inventiones nunca publicó una refutación del artículo de 2015.
Conclusión : Las matemáticas importantes que se han publicado a veces resultan incorrectas. Además, en el futuro seguramente veremos más refutaciones de la evidencia publicada.
Quizás mi trabajo en el área del programa p-adic de Langlands se base en resultados incorrectos. O, de manera más optimista, para obtener resultados correctos, pero para los que no hay pruebas completas.
Si nuestra investigación no es reproducible, ¿podemos llamarla ciencia? Estoy 99,9% seguro de que la humanidad nunca utilizará el programa p-adic de Langlands para hacer algo útil. Si mi trabajo en matemáticas no es útil y está garantizado que sea 100 por ciento correcto, es solo una pérdida de tiempo.... Así que decidí dejar de investigar y concentrarme en probar matemáticas "famosas" en una computadora.
En 2019, Balakrishnan, Dogra, Mueller, Tuitman y Vonk encontraron todas las soluciones racionales para una cierta ecuación de cuarto grado en dos variables. Explícitamente:
Este cálculo tiene una aplicación importante en aritmética. La prueba se basa en gran medida en la computación en magma (un sistema de fuente cerrada) utilizando algoritmos rápidos y sin referencias. Sería difícil trasladar toda la informática a un sistema de código abierto como Sage. Sin embargo, nadie planea hacer esto.
Por lo tanto, parte de la evidencia permanece oculta. Y tal vez permanezca oculto para siempre. ¿Es esta ciencia?
Brechas en matemáticas
- 1993 . .
- 1994 , .
- 1995 , , . , , , . , , , .
¿Qué debe hacer un revisor que recibe un artículo matemático para su revisión? Se argumenta que el trabajo del revisor es "asegurarse de que los métodos utilizados en el artículo sean lo suficientemente sólidos como para demostrar el resultado principal del artículo".
¿Qué pasa si los métodos son sólidos, pero los autores no? Así es como surgen situaciones cuando nuestra evidencia es incompleta. Así es como surge el debate sobre si nuestros teoremas están realmente probados. No es así en absoluto como enseñamos matemáticas a nuestros estudiantes.
Por supuesto, los expertos saben en qué literatura se puede confiar y en cuál no. Pero, ¿tengo que ser un experto para saber en qué literatura puedo confiar?
Grandes lagunas en matemáticas
Anexo A
Clasificación de grupos finitos simples . Los expertos afirman que tenemos una clasificación completa de grupos finitos simples. Confío en los expertos.
- En 1983, se anunció una prueba de clasificación por expertos.
- En 1994, los expertos encontraron un error (¿pero no hagamos volar al elefante de una mosca?)
- En 2004, se publicaron más de 1000 páginas de trabajo. El experto de campo Aschbacher afirma que el error se ha corregido y anuncia un plan para publicar 12 volúmenes de pruebas completas.
- En 2005, solo se publicaron 6 de los 12 volúmenes
- En 2010, solo se publicaron 6 de los 12 volúmenes
- En 2017, solo se publicaron 6 de los 12 volúmenes
- En 2018, se publicaron los volúmenes séptimo y octavo y una nota de que la publicación se completará en 2023.
De las tres personas que lideraban el proyecto, una murió. Los otros dos tienen más de setenta.
Anexo B
Modularidad potencial de superficies abelianas . Hace un año, mi distinguido estudiante de posgrado Toby Gee y tres coautores publicaron una preimpresión de 285 páginas con el resultado de que las superficies abelianas sobre campos completamente reales son potencialmente modulares.
Su prueba cita tres preprints inéditos (uno en 2018, uno en 2015, uno en la década de 1990), un memorando de Internet de 2007, una disertación inédita en alemán y un artículo cuya afirmación principal fue luego refutada. Además, en la página 13 vemos el siguiente texto:
, Arthur’s multiplicity formula GSp4, [Art04]. , , [GT18], , [Art13] [MW16a, MW16b]. , twisted weighted fundamental lemma, [CL10], . , [A24], [A25], [A26] [A27] [Art13], .¿Podemos decir honestamente que esto es ciencia?
El enlace [CL10] se ve así: El
trabajo que necesitan mi estudiante de posgrado y mis coautores nunca ha sido publicado. Lo más probable es que la afirmación sea correcta. Quizás incluso demostrable.
Y estos son los enlaces a los que se hace referencia de [Art13]:
El año pasado le pregunté a Arthur sobre estos enlaces y me dijo que ninguno de los trabajos estaba listo todavía. Por supuesto, Jim Arthur es un genio. Ha ganado numerosos premios de prestigio. Pero también tiene 75 años.
Anexo C
Gaitsgory - Rozenblyum . Un sinfín de categorías han ganado popularidad últimamente. Se volverán aún más importantes con el tiempo. El trabajo del laureado Fields, Peter Scholze, se basa en un sinfín de categorías.
Jacob Lurie ha escrito un trabajo de más de 1000 páginas sobre
-categorizado e incluido muchos detalles en mi trabajo. Gaitsgory - Rozenblyum quería resultados similares para
-categorías, pero omitió muchos de los argumentos para ahorrar tiempo. "La evidencia omitida aparecerá en otro lugar".
Le pregunté a Gaitsgory cuánto faltaba. Él respondió que eran unas 100 páginas. Le pregunté a Lurie qué pensaba de esto. Él respondió que "los matemáticos difieren mucho en lo cómodos que se sienten al omitir detalles".
¿Las matemáticas se mueven demasiado rápido? Si soy un “experto”, ¿debería creer que las superficies abelianas sobre campos totalmente reales son potencialmente modulares? Para ser honesto, ya no me conozco.
En una conferencia en la Universidad Carnegie Mellon donde estuve la semana pasada, Markus Rabe me dijo que Google está trabajando en un programa que traducirá preprints matemáticos de arxiv.orgen un lenguaje adecuado para la verificación por computadora. También vi recientemente un trabajo que se basa en un artículo de mi alumno, pero no menciona nada sobre las 100 páginas que faltan en [Art13].
Último error
Este es un ejemplo muy interesante. El trabajo original fue publicado en J. Funct. Anal. en 2013. Hay un gran error en el trabajo (desigualdad en la otra dirección). El error fue descubierto por S. Gouezel en 2017, cuando Gouezel formalizó una discusión utilizando un programa de verificación de pruebas computarizado (Isabelle).
Gouezel y el autor del trabajo original presentan un nuevo argumento. El nuevo trabajo no necesita revisión. La computadora verificó el 100 por ciento del nuevo argumento. Los métodos resultaron ser lo suficientemente sólidos como para probar el teorema. Y por "prueba" me refiero a la definición clásica y "pura" de prueba: aquello que enseñamos a nuestros estudiantes. Cada detalle de la prueba está disponible para el lector. La ciencia es reproducible. Estas son las matemáticas que enseñamos a nuestros estudiantes. Esto es matemática.
Aquí hay otros ejemplos de lo que creo que son matemáticas:
- Prueba típica de estudiante o nivel de maestría
- Prueba típica de hace 100 años de un resultado importante que ha sido bien documentado e investigado por decenas de miles de matemáticos
- Prueba formal de Gonthier, Asperti, Avigad, Bertot, Cohen, Garillot, Le Roux, Mahboubi, O'Connor, Ould Biha, Pasca, Rideau, Solovyev, Tassi, Théry del teorema de Feith-Thompson.
- Prueba formal de autoría de los siguientes matemáticos: Hales, Adams, Bauer, Dat Tat Dang, Harrison, Truong Le Hoang, Kaliszyk, Magron, McLaughlin, Thang Tat Nguyen, Truong Quang Nguyen, Nipkow, Obua, Pleso, Rute, Solovyev, An Hoai Thi Ta , Trung Nam Tran, Diep Thi Trieu, Urban, Ky Khac Vu y la prueba de Zumkeller de la conjetura de Kepler.
Con esto concluye el texto de la presentación, porque Kevin pasa a su parte principal: verificación formal de demostraciones matemáticas en Lean, desarrollada por Leo de Moura en Microsoft Research. Desafortunadamente, no se incluyeron ejemplos en las diapositivas.
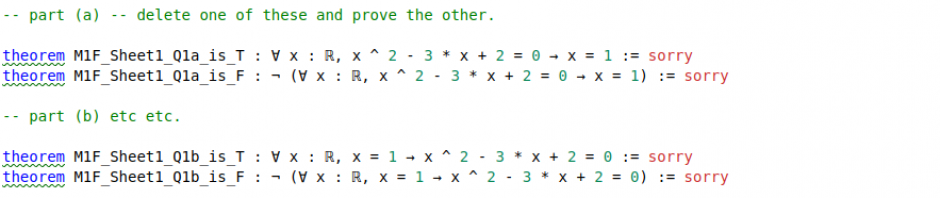
El autor es un gran entusiasta de la verificación formal de pruebas matemáticas y tiene un blog de Xena muy interesante sobre este tema que recomiendo encarecidamente.