
Los problemas de seguridad de la información requieren el estudio y la solución de una serie de problemas teóricos y prácticos en la interacción de la información de los suscriptores del sistema. Nuestra doctrina de seguridad de la información formula la tarea trina de garantizar la integridad, confidencialidad y disponibilidad de la información. Los artículos aquí presentados están dedicados a la consideración de problemas específicos de su solución en el marco de varios sistemas y subsistemas estatales. Anteriormente, el autor consideró en 5 artículos los temas de asegurar la confidencialidad de los mensajes mediante estándares estatales. El concepto general del sistema de codificación también lo di anteriormente .
Introducción
Por mi educación básica, no soy un matemático, pero en relación con las disciplinas que leo en la universidad, tenía que entenderlo meticulosamente. Durante mucho tiempo y con persistencia leí los libros de texto clásicos de nuestras principales universidades, una enciclopedia matemática de cinco volúmenes, muchos folletos populares delgados sobre temas específicos, pero la satisfacción no surgió. Tampoco surgió la comprensión lectora profunda.
Todos los clásicos matemáticos se centran, por regla general, en el caso teórico infinito, y las disciplinas especiales se basan en el caso de construcciones finitas y estructuras matemáticas. La diferencia de enfoques es colosal, la ausencia o falta de buenos ejemplos completos es quizás la principal desventaja y falta de libros de texto universitarios. Rara vez hay un libro de problemas con soluciones para principiantes (para estudiantes de primer año), y los que existen pecan con omisiones en las explicaciones. En general, me enamoré de las librerías técnicas de segunda mano, gracias a las cuales se reponía la biblioteca y, en cierta medida, el acervo de conocimientos. Tuve la oportunidad de leer mucho, mucho, pero "no fui".
Este camino me llevó a la pregunta, ¿qué puedo hacer yo solo sin "muletas" de libros, teniendo frente a mí solo una hoja de papel en blanco y un lápiz con goma de borrar? Resultó ser bastante y no exactamente lo que se necesitaba. Se superó el difícil camino de la autoeducación al azar. La pregunta era esta. ¿Puedo construir y explicar, en primer lugar a mí mismo, el trabajo del código que detecta y corrige errores, por ejemplo, código Hamming, (7, 4) -code?
Se sabe que el código Hamming se usa ampliamente en muchas aplicaciones en el campo del almacenamiento e intercambio de datos, especialmente en RAID; además, está en la memoria ECC y permite la corrección sobre la marcha de errores simples y dobles.
Seguridad de información. Códigos, cifrados, mensajes steg
La interacción de la información a través del intercambio de mensajes entre sus participantes debe estar protegida en diferentes niveles y por diversos medios, tanto hardware como software. Estas herramientas se desarrollan, diseñan y crean en el marco de ciertas teorías (ver Figura A) y tecnologías adoptadas por acuerdos internacionales sobre modelos OSI / ISO.
La protección de la información en los sistemas de telecomunicaciones de la información (ITS) se está convirtiendo prácticamente en el principal problema en la resolución de problemas de gestión, tanto a escala individual - usuario, como para empresas, asociaciones, departamentos y el estado en su conjunto. De todos los aspectos de la protección ITKS, en este artículo consideraremos la protección de la información durante su extracción, procesamiento, almacenamiento y transmisión en los sistemas de comunicación.
Aclarando aún más el área temática, nos centraremos en dos posibles direcciones en las que se consideran dos enfoques diferentes para la protección, presentación y uso de la información: sintáctico y semántico. En la figura se utilizan las siguientes abreviaturas: códec - códec - decodificador; shidesh — un decodificador-decodificador; chillido - corrector - extractor.
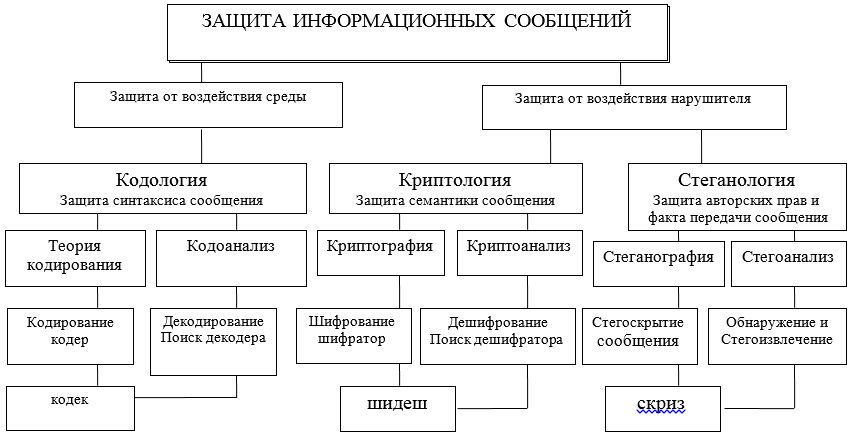
Figura A - Diagrama de las principales direcciones e interrelaciones de las teorías destinadas a resolver los problemas de protección de la interacción de la información
Las características sintácticas de la presentación de mensajes le permiten controlar y garantizar la corrección y precisión (sin errores, integridad) de la presentación durante el almacenamiento, procesamiento y especialmente al transferir información a través de canales de comunicación. Aquí, los principales problemas de protección se resuelven mediante los métodos de codología, su gran parte: la teoría de la corrección de códigos.
Seguridad semántica (semántica)los mensajes son proporcionados por métodos de criptología, que por medio de la criptografía permite proteger a un intruso potencial de dominar el contenido de la información. Al mismo tiempo, el infractor puede copiar, robar, cambiar o reemplazar, o incluso destruir el mensaje y su portador, pero no podrá obtener información sobre el contenido y significado del mensaje transmitido. El contenido de la información en el mensaje permanecerá inaccesible para el delincuente. Por lo tanto, el tema de mayor consideración será la protección sintáctica y semántica de la información en el ITCS. En este artículo, nos limitaremos a considerar solo el enfoque sintáctico en una implementación simple pero muy importante del mismo mediante la corrección de código. Trazaré
inmediatamente una línea divisoria en la resolución de problemas de seguridad de la información: la
teoría de la codologíadiseñado para proteger la información (mensajes) de errores (protección y análisis de la sintaxis de los mensajes) del canal y el entorno, para detectar y corregir errores;
la teoría de la criptología está diseñada para proteger la información del acceso no autorizado a su semántica por parte del intruso (protección de la semántica, el significado de los mensajes);
la teoría de la esteganología está diseñada para proteger el hecho del intercambio de información de mensajes, así como para proteger los derechos de autor, los datos personales (protección del secreto médico).
En general, vamos. Por definición, y hay bastantes de ellos, ni siquiera es fácil entender que existe un código. Los autores escriben que el código es un algoritmo, una pantalla y algo más. No escribiré sobre la clasificación de códigos aquí, solo diré que el código (7, 4) es bloque .
En algún momento, me di cuenta de que el código son palabras de código especial, un conjunto finito de ellas, que se reemplazan por algoritmos especiales con el texto original del mensaje en el lado de transmisión del canal de comunicación y que se envían a través del canal al destinatario. La sustitución la realiza el dispositivo codificador y, en el lado de recepción, estas palabras son reconocidas por el dispositivo decodificador.
Dado que el papel de las partes es variable, ambos dispositivos se combinan en uno y se denominan códec abreviado (codificador / descodificador) y se instalan en ambos extremos del canal. Además, dado que hay palabras, también hay un alfabeto. El alfabeto consta de dos caracteres {0, 1}, en tecnología, bloque binariocódigos. El alfabeto de lenguaje natural (NL) es un conjunto de símbolos, letras que reemplazan los sonidos del habla oral al escribir. Aquí no profundizaremos en la escritura jeroglífica en escritura silábica o nodular.
El alfabeto y las palabras ya son un lenguaje, se sabe que los lenguajes humanos naturales son redundantes, pero lo que esto significa, donde habita la redundancia del lenguaje es difícil de decir, la redundancia no está muy bien organizada, caótica. Al codificar, almacenar información, tienden a reducir la redundancia, por ejemplo, archivadores, código Morse, etc.
Richard Hemming probablemente se dio cuenta antes que otros de que si la redundancia no se elimina, sino que se organiza razonablemente, entonces se puede utilizar en los sistemas de comunicación para detectar errores y corregirlos automáticamente en las palabras de código del texto transmitido. Se dio cuenta de que las 128 palabras binarias de 7 bits se pueden usar para detectar errores en palabras de código que forman un código, un subconjunto de 16 palabras binarias de 7 bits. Fue una suposición brillante.
Antes de la invención de Hamming, el lado receptor también detectaba errores cuando el texto decodificado no se podía leer o no resultaba exactamente lo que se necesitaba. Al mismo tiempo, se envió una solicitud al remitente del mensaje para que repitiera los bloques de determinadas palabras, lo que, por supuesto, resultó muy inconveniente y ralentizó las sesiones de comunicación. Este era un gran problema que no se había resuelto durante décadas.
Construcción de un código Hamming (7, 4)
Volvamos a Hamming. Las palabras del código (7, 4) se forman a partir de 7 bits j = , j = 0 (1) 15, 4 símbolos de información y 3 de verificación, es decir esencialmente redundantes, ya que no llevan información de mensaje. Fue posible representar estos tres dígitos de control mediante funciones lineales de 4 símbolos de información en cada palabra, lo que aseguró la detección del hecho de un error y su lugar en palabras para realizar una corrección. Un código (7, 4) obtuvo un nuevo adjetivo y se convirtió en unbinario de bloque lineal. Dependencias funcionales lineales (reglas (*)) para calcular valores de símbolo
son los siguientes:
La corrección del error se convirtió en una operación muy simple: se determinó un carácter (cero o uno) en el bit erróneo y se reemplazó con otro opuesto a 0 por 1 o 1 por 0. ¿Cuántas palabras diferentes forman el código? La respuesta a esta pregunta para el código (7, 4) es muy simple. Dado que solo hay 4 bits de información, y su variedad cuando están llenos de símbolos
= 16 opciones, entonces simplemente no hay otras posibilidades, es decir, un código que consta de solo 16 palabras asegura que estas 16 palabras representan la escritura completa de todo el idioma. Las partes informativas de estas 16 palabras están numeradas # (
): 0 = 0000; 4 = 0100; 8 = 1000; 12 = 1100; 1 = 0001; 5 = 0101; 9 = 1001; 13 = 1101; 2 = 0010; 6 = 0110; 10 = 1010; 14 = 1110; 3 = 0011; 7 = 0111; 11 = 1011; 15 = 1111. Cada una de estas palabras de 4 bits debe calcularse y agregarse a la derecha con 3 bits de verificación, que se calculan de acuerdo con las reglas (*). Por ejemplo, para la palabra de información No. 6 igual a 0110, tenemos
y los cálculos de los símbolos de verificación dan el siguiente resultado para esta palabra:
La sexta palabra de código en este caso toma la forma:De la misma manera, es necesario calcular los símbolos de verificación para las 16 palabras de código. Preparemos una tabla K de 16 líneas para las palabras de código y completemos secuencialmente sus celdas (recomiendo al lector que lo haga con un lápiz en la mano).Tabla K - palabras de código j, j = 0 (1) 15, (7, 4) - Códigos de Hamming
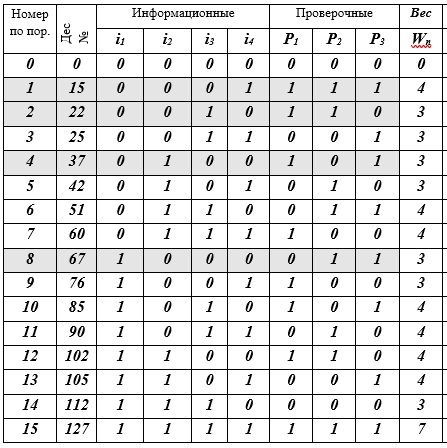
Descripción de la tabla: 16 líneas - palabras de código; 10 columnas: número de secuencia, representación decimal de la palabra de código, 4 símbolos de información, 3 símbolos de verificación, peso W de la palabra de código es igual al número de bits distintos de cero (≠ 0). Se resaltan 4 líneas de palabras de código rellenando: esta es la base del subespacio vectorial. En realidad, eso es todo: el código está construido.
Por lo tanto, la tabla contiene todas las palabras (7, 4): el código Hamming. Como ves, no fue muy difícil. A continuación, hablaremos sobre las ideas que llevaron a Hamming a esta construcción de código. Todos estamos familiarizados con el código Morse, con el alfabeto semáforo naval y otros sistemas construidos sobre diferentes principios heurísticos, pero aquí en el código (7, 4), se utilizan principios y métodos matemáticos rigurosos por primera vez. La historia será solo sobre ellos.
Fundamentos matemáticos del código. Álgebra superior
Ha llegado el momento de contar cómo a R. Hemming se le ocurrió la idea de abrir tal código. No se hacía ilusiones especiales sobre su talento y modestamente se formuló una tarea: crear un código que detectara y corrigiera un error en cada palabra (de hecho, se detectaron incluso dos errores, pero solo se corrigió uno de ellos). Con canales de calidad, incluso un error es un evento raro. Por lo tanto, el plan de Hemming seguía siendo grandioso en la escala del sistema de comunicaciones. Hubo una revolución en la teoría de la codificación después de su publicación.
Era 1950. Doy aquí mi descripción simple (espero, comprensible), que no he visto de otros autores, pero resultó que no todo es tan simple. Se necesitaron conocimientos de numerosas áreas de las matemáticas y tiempo para comprender todo profundamente y comprender por sí mismo por qué se hace de esta manera. Solo después de eso pude apreciar la hermosa y bastante simple idea que se implementa en este código de corrección. La mayor parte del tiempo lo dediqué a abordar la técnica de los cálculos y la justificación teórica de todas las acciones sobre las que estoy escribiendo aquí.
Los creadores de los códigos, durante mucho tiempo, no pudieron pensar en un código que detecte y corrija dos errores. Las ideas utilizadas por Hemming no funcionaron allí. Tuve que buscar y se encontraron nuevas ideas. ¡Muy interesante! Cautiva. Se necesitaron alrededor de 10 años para encontrar nuevas ideas, y solo después de eso hubo un gran avance. Los códigos que muestran un número arbitrario de errores se recibieron con relativa rapidez.
Espacios vectoriales, campos y grupos . El código (7, 4) resultante (Tabla K) representa un conjunto de palabras de código que son elementos de un subespacio vectorial (de orden 16, con dimensión 4), es decir parte de un espacio vectorial de dimensión 7 con orden De las 128 palabras, solo 16 están incluidas en el código, pero se incluyeron en el código por una razón. Primero, son un subespacio con todas las propiedades y singularidades resultantes; segundo, las palabras de código son un subgrupo de un gran grupo de orden 128, incluso además, un subgrupo aditivo de un campo de Galois extendido finito GF (
) grado de expansión n = 7 y características 2. Este gran subgrupo está descompuesto en clases adyacentes por un subgrupo más pequeño, que se ilustra bien en la siguiente tabla D. La tabla está dividida en dos partes: superior e inferior, pero debe leerse como una larga. Cada clase adyacente (fila de la tabla) es un elemento del grupo de factores por la equivalencia de componentes. Tabla D - Descomposición del grupo de aditivos del campo Galois GF (
) en clases laterales (filas de la tabla D) para un subgrupo de orden 16.
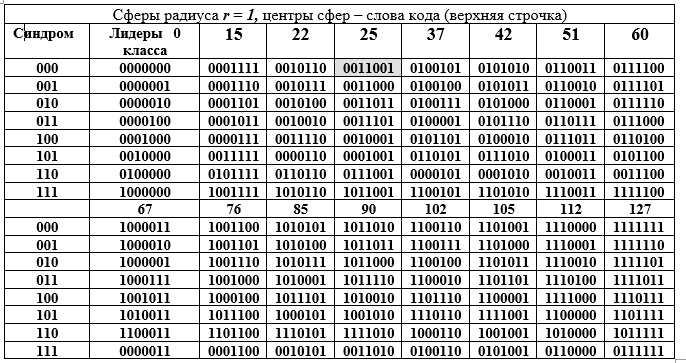
Las columnas de la tabla son esferas de radio 1. La columna de la izquierda (repetida) es el síndrome de la palabra (7, 4) código de Hamming, la siguiente columna son los líderes de la clase contigua. Abramos la representación binaria de uno de los elementos (el 25 se resalta llenando) del grupo de factores y su representación decimal:
Técnica para obtener filas de la tabla D. Un elemento de la columna de líderes de la clase se suma con cada elemento del encabezado de la columna de la tabla D (la suma se realiza para la fila del líder en forma binaria mod2) Dado que todos los líderes de clase tienen un peso W = 1, entonces todas las sumas difieren de la palabra en el encabezado de la columna en una sola posición (la misma para toda la fila, pero diferente para la columna). La tabla D tiene una maravillosa interpretación geométrica. Las 16 palabras de código están representadas por los centros de las esferas en el espacio vectorial de 7 dimensiones. Todas las palabras de la columna difieren de la palabra superior en la misma posición, es decir, se encuentran en la superficie de una esfera con radio r = 1.
Esta interpretación esconde la idea de detectar un error en cualquier palabra de código. Trabajamos con esferas. La primera condición para la detección de errores es que las esferas de radio 1 no deben tocarse ni cruzarse. Esto significa que los centros de las esferas están a una distancia de 3 o más entre sí. En este caso, las esferas no solo no se cruzan, sino que tampoco se tocan entre sí. Este es un requisito para la falta de ambigüedad de la decisión: qué esfera debe atribuirse a la palabra errónea recibida en el lado receptor por el decodificador (no un código uno de 128-16 = 112).
En segundo lugar, el conjunto completo de palabras binarias de 7 bits de 128 palabras se distribuye uniformemente en 16 esferas. El decodificador solo puede obtener una palabra de este conjunto de 128 palabras conocidas con o sin error. En tercer lugar, el lado receptor puede recibir una palabra sin error o con distorsión, pero siempre perteneciente a una de las 16 esferas, que es fácilmente determinada por el decodificador. En la última situación, se toma la decisión de que se envió una palabra de código: el centro de una esfera determinado por el decodificador, que encontró la posición (intersección de una fila y una columna) de la palabra en la tabla D, es decir, los números de columna y fila.
Aquí surge un requisito para las palabras del código y para el código en su conjunto: la distancia entre dos palabras de código cualesquiera debe ser de al menos tres, es decir, la diferencia para un par de palabras de código, por ejemplo, Ci = 85 == 1010101; j = 25 == 0011001 debe ser al menos 3; 85 - 25 = 1010101 - 0011001 = 1001100 = 76, el peso de la palabra de diferencia W (76) = 3. (La Tabla D reemplaza el cálculo de diferencias y sumas). Aquí, la distancia entre los vectores de palabras binarias se entiende como el número de posiciones no coincidentes en dos palabras. Esta es la distancia de Hamming, que se ha vuelto muy utilizada en la teoría y en la práctica, ya que satisface todos los axiomas de distancia.
Observación . El código (7, 4) no es solo un código binario de bloque lineal , sino que también es un código de grupo , es decir, las palabras del código forman un grupo algebraico por adición. Esto significa que dos palabras de código cualesquiera, cuando se suman, dan de nuevo una de las palabras de código. Solo que esta no es una operación de suma ordinaria, es una suma módulo dos.
Tabla E: la suma de los elementos del grupo (palabras de código) utilizados para construir el código de Hamming
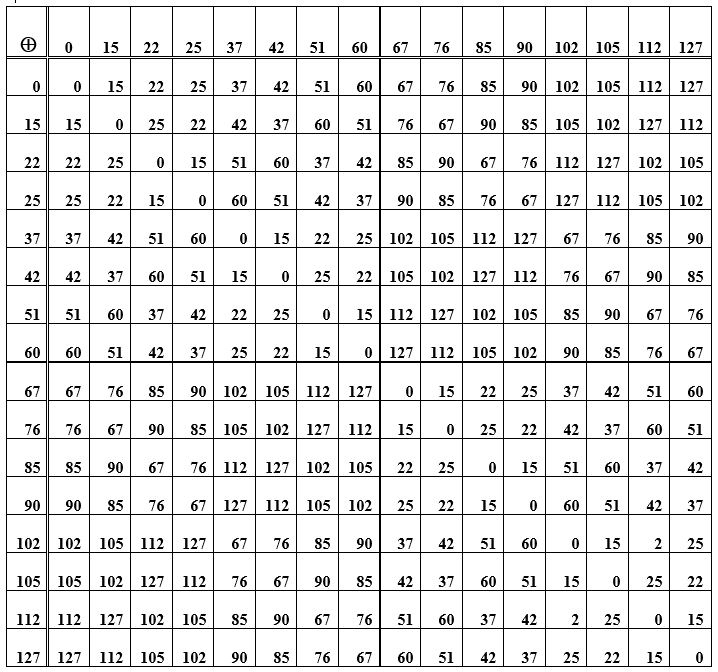
La operación de sumar palabras en sí es asociativa, y para cada elemento en el conjunto de palabras de código hay un opuesto, es decir, sumar la palabra original con el opuesto da valor cero. Esta palabra de código cero es el elemento neutral del grupo. En la tabla D, esta es la diagonal principal de ceros. El resto de las celdas (intersecciones fila / columna) son representaciones numéricas-decimales de palabras de código obtenidas sumando elementos de una fila y una columna. Cuando reorganiza las palabras en lugares (al sumar), el resultado sigue siendo el mismo; además, la resta y la suma de palabras tienen el mismo resultado. Además, se considera un sistema de codificación / decodificación que implemente el principio sindrómico.
Aplicación de código. Descifrador
El codificador está ubicado en el lado de transmisión del canal y es utilizado por el remitente del mensaje. El remitente del mensaje (el autor) forma el mensaje en el alfabeto del lenguaje natural y lo presenta en forma digital. (El nombre del carácter en código ASCII y en binario).
Es conveniente generar textos en archivos para una PC utilizando un teclado estándar (códigos ASCII). Cada carácter (letra del alfabeto) corresponde a un octeto de bits (ocho bits) en esta codificación. Para el código (7, 4) - Hamming, en cuyas palabras hay solo 4 símbolos de información, al codificar un símbolo de teclado por letra, se requieren dos palabras de código, es decir, un octeto de una letra se divide en dos palabras de información del lenguaje natural (NL) del formulario
...
Ejemplo 1 . Es necesario transferir la palabra "dígito" en NL. Ingresamos a la tabla de códigos ASCII, las letras corresponden a: c –11110110, y –11101000, f - 11110100, p - 11110000, y - 11100000 octetos. O de lo contrario, en códigos ASCII, la palabra "dígito" = 1111 0110 1110 1000 1111 0100 1111 0000 1110 0000
con un desglose en tétradas (4 dígitos cada uno). Por tanto, la codificación de la palabra "dígito" NL requiere 10 palabras de código del código Hamming (7, 4). Las tétradas representan los bits informativos de las palabras del mensaje. Estas palabras de información (tétradas) se convierten en palabras de código (de 7 bits cada una) antes de enviarse al canal de la red de comunicación. Esto se hace mediante la multiplicación de matrices vectoriales: la palabra de información por la matriz generadora. El pago por conveniencia es muy costoso y requiere mucho tiempo, pero todo funciona automáticamente y, lo más importante, el mensaje está protegido contra errores.
La matriz generadora del código Hamming (7, 4) o el generador de palabras de código se obtiene escribiendo los vectores base del código y combinándolos en una matriz. Esto se sigue del teorema del álgebra lineal: cualquier vector de un espacio (subespacio) es una combinación lineal de vectores básicos, es decir, linealmente independientes en este espacio. Esto es exactamente lo que se requiere: generar cualquier vector (palabras de código de 7 bits) a partir de información de 4 bits.
La matriz generadora del código Hamming (7, 4, 3) o el generador de palabras de código tiene la forma:
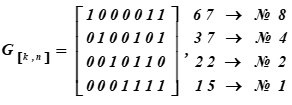
A la derecha están las representaciones decimales de las palabras de código de la Base del subespacio y sus números de serie en la tabla K
No. i filas de la matriz son las palabras del código que son la base del subespacio vectorial.
Un ejemplo de codificación de palabras de mensajes de información (la matriz generadora del código se construye a partir de los vectores base y corresponde a la parte de la tabla K). En la tabla de códigos ASCII, tomamos la letra q = <1111 0110>.
Las palabras de información del mensaje se ven así:
...
Estos son la mitad del carácter (c). Para el código (7, 4) definido anteriormente, se requiere encontrar las palabras de código correspondientes a la palabra de mensaje de información (c) de 8 caracteres en la forma:
...
Para convertir este mensaje de letra (q) en palabras de código u, cada mitad del mensaje de letra i se multiplica por la matriz generadora G [k, n] del código (matriz para la tabla K):
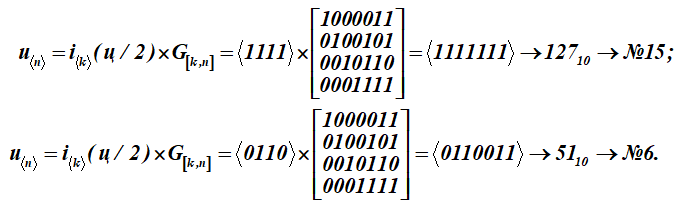
Tenemos dos palabras de código con números de serie 15 y 6.
Mostrar formación detallada del resultado inferior No. 6 - una palabra de código (multiplicación de la fila de la palabra de información por las columnas de la matriz generadora); suma sobre (mod2)
<0110> ∙ <1000> = 0 ∙ 1 + 1 ∙ 0 + 1 ∙ 0 + 0 ∙ 0 = 0 (mod2);
<0110> ∙ <0100> = 0 ∙ 0 + 1 ∙ 1 + 1 ∙ 0 + 0 ∙ 0 = 1 (mod2);
<0110> ∙ <0010> = 0 ∙ 0 + 1 ∙ 0 + 1 ∙ 1 + 0 ∙ 0 = 1 (mod2);
<0110> ∙ <0001> = 0 ∙ 0 + 1 ∙ 0 + 1 ∙ 0 + 0 ∙ 1 = 0 (mod2);
<0110> ∙ <0111> = 0 ∙ 0 + 1 ∙ 1 + 1 ∙ 1 + 0 ∙ 1 = 0 (mod2);
<0110> ∙ <1011>= 0 ∙ 1 + 1 ∙ 0 + 1 ∙ 1 + 0 ∙ 1 = 1 (mod2);
<0110> ∙ <1101> = 0 ∙ 1 + 1 ∙ 1 + 1 ∙ 0 + 0 ∙ 1 = 1 (mod2).
Recibido como resultado de la multiplicación de las palabras decimoquinta y sexta de la Tabla K. Los primeros cuatro bits de estas palabras de código (resultados de la multiplicación) representan palabras de información. Parecen:, (en la tabla ASCII es solo la mitad de la letra t). Para la matriz de codificación, el conjunto de palabras con los números: 1, 2, 4, 8 se seleccionan como vectores base en la tabla K. En la tabla se resaltan llenando. Entonces, para esta tabla K, la matriz de codificación recibirá la forma G [k, n].
Como resultado de la multiplicación, se obtuvieron 15 y 6 palabras de la tabla de códigos K.
Aplicación de código. Descifrador
El decodificador está ubicado en el lado receptor del canal donde está el receptor del mensaje. El propósito del decodificador es proporcionar al destinatario el mensaje transmitido en la forma en que existía en el remitente en el momento del envío, es decir el destinatario puede utilizar el texto y utilizar la información del mismo para su trabajo posterior.
La tarea principal del decodificador es verificar si la palabra recibida (7 bits) es la que se envió en el lado transmisor, si la palabra contiene errores. Para resolver este problema, por cada palabra recibida por el decodificador, multiplicándola por la matriz de verificación [nk, n], se calcula un síndrome de vector corto S (3 bits).
Para las palabras que son código, es decir, que no contienen errores, el síndrome siempre toma un valor cero S = <000>. Para una palabra con error, el síndrome no es cero S ≠ 0.El valor del síndrome permite detectar y localizar la posición del error hasta un bit en la palabra recibida en el lado receptor y el decodificador puede cambiar el valor de este bit. En la matriz de verificación del código, el decodificador encuentra una columna que coincide con el valor del síndrome, y el número ordinal de esta columna es igual al bit corrompido por el error. Después de eso, para los códigos binarios, el decodificador cambia este bit, simplemente reemplácelo con el valor opuesto, es decir, uno se reemplaza por cero y cero se reemplaza por uno.
El código en cuestión es sistemático, es decir, los símbolos de la palabra de información se colocan en una fila en los bits más significativos de la palabra de código. La recuperación de palabras de información se realiza simplemente descartando los bits menos significativos (de verificación), cuyo número se conoce. Además, se utiliza una tabla de códigos ASCII en orden inverso: la entrada son secuencias binarias informativas y la salida son las letras del alfabeto del lenguaje natural. Entonces, el código (7, 4) es sistemático, grupal, lineal, de bloque, binario .
La base del decodificador está formada por la matriz de verificación H [nk, n], que contiene el número de filas igual al número de símbolos de verificación, y todas las columnas posibles, excepto cero, columnas de tres caracteres... La matriz de verificación de paridad se construye a partir de las palabras de la tabla K, se eligen de modo que sean ortogonales a la matriz de codificación, es decir, su producto es la matriz cero. La matriz de verificación toma la siguiente forma en las operaciones de multiplicación, se transpone. Para un ejemplo específico, la matriz de verificación H [nk, n] se da a continuación:
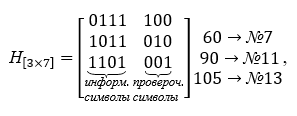



Vemos que el producto de la matriz generadora y la matriz de verificación da como resultado una matriz cero.
Ejemplo 2. Decodificación de una palabra del código Hamming sin error (e <7> = <0000000>).
Sea en el extremo receptor del canal las palabras recibidas # 7 → 60 y # 13 → 105 de la tabla K,
u <7> + e <7> = <0 1 1 1 1 0 0> + <0 0 0 0 0 0 0>,
donde no hay error, es decir, tiene la forma e <7> = <0 0 0 0 0 0 0>.

Como resultado, el síndrome calculado tiene un valor cero, lo que confirma la ausencia de un error en las palabras del código.
Ejemplo 3 . Detección de un error en una palabra recibida en el extremo receptor del canal (Tabla K).
A) Suponga que se requiere transmitir la séptima palabra de código, es decir
u <7> = <0 1 1 1 1 0 0> y en un tercio desde la izquierda de la palabra, se cometió un error. Luego se suma mod2 con la séptima palabra de código transmitida por el canal de comunicación
u <7> + <7> = <0 1 1 1 1 0 0> + <0 0 1 0 0 0 0> = <0 1 0 1 1 0 0>,
donde el error tiene la forma e <7> = <0 0 1 0 0 0 0>.
El establecimiento del hecho de la distorsión de la palabra de código se realiza multiplicando la palabra distorsionada recibida por la matriz de verificación del código. El resultado de esta multiplicación será un vectorllamado síndrome de palabra clave.
Realicemos tal multiplicación para nuestros datos originales (séptimo vector con error).

Como resultado de tal multiplicación, en el extremo receptor del canal, se obtuvo un síndrome de vector S <nk>, cuya dimensión es (n - k). Si el síndrome S <3> = <0,0,0> es cero, se concluye que la palabra recibida en el lado receptor pertenece al código C y se transmite sin distorsión. Si el síndrome no es igual a cero S <3> ≠ <0,0,0>, entonces su valor indica la presencia de un error y su lugar en la palabra. El bit distorsionado corresponde al número de la posición de la columna de la matriz [nk, n], que coincide con el síndrome. Después de eso, se corrige el bit distorsionado y el decodificador procesa más la palabra recibida. En la práctica, se calcula inmediatamente un síndrome para cada palabra aceptada y, si hay un error, se elimina automáticamente.
Entonces, durante los cálculos, el síndrome S = <110> es el mismo para ambas palabras. Observamos la matriz de verificación y encontramos la columna que coincide con el síndrome. Esta es la tercera columna de la izquierda. Por tanto, el error se cometió en el tercer dígito de la izquierda, que coincide con las condiciones del ejemplo. Este tercer bit se cambia al valor opuesto y devolvimos las palabras recibidas por el decodificador al formato de código. El error fue encontrado y solucionado.
Eso es todo, así es como funciona y funciona el código Hamming clásico (7, 4).
No se consideran aquí numerosas modificaciones y actualizaciones de este código, ya que no son ellas las que son importantes, sino aquellas ideas y sus implementaciones que cambiaron radicalmente la teoría de la codificación y, como resultado, los sistemas de comunicación, el intercambio de información, los sistemas de control automatizados.
Conclusión
El documento considera las principales disposiciones y tareas de la seguridad de la información, nombra las teorías diseñadas para resolver estos problemas.
La tarea de proteger la interacción de información de sujetos y objetos de errores ambientales y de las acciones del intruso pertenece a la codología.
El código de Hamming (7, 4) se considera en detalle, lo que sentó las bases para una nueva dirección en la teoría de la codificación: la síntesis de códigos correctores.
Se muestra la aplicación de rigurosos métodos matemáticos utilizados en la síntesis de código.
Se dan ejemplos para ilustrar la eficiencia del código.
Literatura
Peterson W., Weldon E. Códigos de corrección de errores: Trans. De inglés. M.: Mir, 1976, 594 p.
Bleihut R. Teoría y práctica de los códigos de control de errores. Traducido del inglés. M.: Mir, 1986, 576 p.