Introducción
La arquitectura de la Red neuronal convolucional (CNN) RetinaNet consta de 4 partes principales, cada una de las cuales tiene su propio propósito:
a) Backbone: la red principal (básica) utilizada para extraer características de la imagen de entrada. Esta parte de la red es variable y puede incluir redes neuronales de clasificación como ResNet, VGG, EfficientNet y otras;
b) Feature Pyramid Net (FPN): una red neuronal convolucional, construida en forma de pirámide, que sirve para combinar las ventajas de los mapas de características de los niveles inferior y superior de la red; los primeros tienen una capacidad de generalización de alta resolución, pero de baja semántica; los últimos son lo contrario;
c) Subred de clasificación: una subred que extrae información sobre las clases de objetos de FPN, resolviendo el problema de clasificación;
d) Subred de regresión: una subred que extrae información sobre las coordenadas de objetos en la imagen desde FPN, resolviendo el problema de regresión.
En la Fig. 1 muestra la arquitectura de RetinaNet con la red neuronal ResNet como la red troncal.
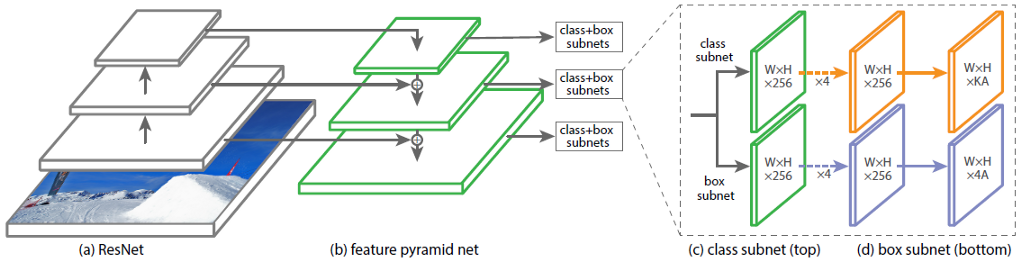
Figura 1 - Arquitectura RetinaNet con una red troncal ResNet
Analicemos en detalle cada una de las partes RetinaNet que se muestran en la Fig. 1)
Backbone es parte de la red RetinaNet
Teniendo en cuenta que la parte de la arquitectura RetinaNet que acepta una imagen como entrada y destaca características importantes es variable y la información extraída de esta parte se procesará en las siguientes etapas, es importante elegir una red troncal adecuada para obtener los mejores resultados.
Investigaciones recientes sobre la optimización de CNN han llevado al desarrollo de modelos de clasificación que superan a todas las arquitecturas desarrolladas previamente con las mejores tasas de precisión en el conjunto de datos ImageNet, al tiempo que mejoran la eficiencia en 10 veces. Estas redes se llamaron EfficientNet-B (0-7). Los indicadores de la familia de nuevas redes se muestran en la Fig. 2.
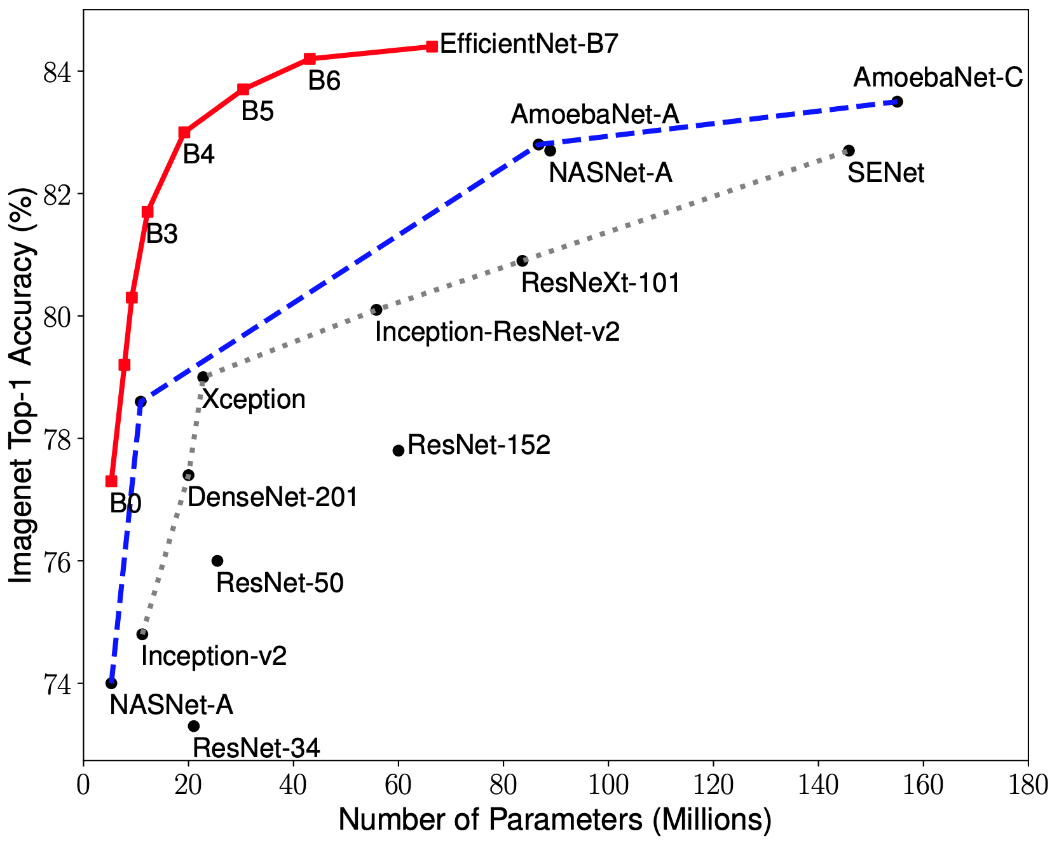
Figura 2 - Gráfico de la dependencia del indicador de mayor precisión en el número de pesos de red para varias arquitecturas
La pirámide de signos
La Feature Pyramid Network consta de tres partes principales: vía ascendente, vía descendente y conexiones laterales.
El camino ascendente es una especie de "pirámide" jerárquica, una secuencia de capas convolucionales con dimensión decreciente, en nuestro caso, una red troncal. Las capas superiores de la red convolucional tienen un significado más semántico, pero una resolución más baja, y las más bajas, por el contrario (Fig. 3). La ruta de abajo hacia arriba tiene una vulnerabilidad en la extracción de características: la pérdida de información importante sobre un objeto, por ejemplo, debido al ruido de un objeto pequeño pero significativo en el fondo, ya que al final de la red la información está muy comprimida y generalizada.
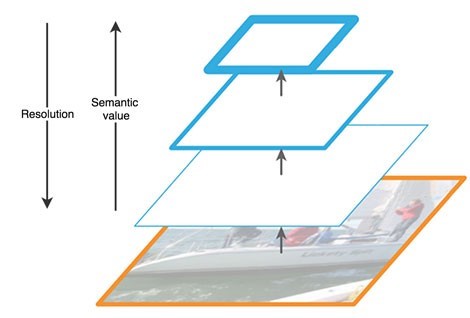
Figura 3 - Características de los mapas de características en diferentes niveles de la red neuronal
El camino descendente es también una "pirámide". Los mapas de características de la capa superior de esta pirámide tienen el tamaño de los mapas de características de la capa superior de abajo hacia arriba de la pirámide y se duplican con el método vecino más cercano (Fig. 4) hacia abajo.
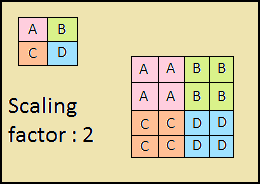
Figura 4: aumento de la resolución de la imagen mediante el método vecino más cercano
Por lo tanto, en la red de arriba hacia abajo, cada mapa de características de la capa superior se incrementa al tamaño del mapa subyacente. Además, las conexiones laterales están presentes en FPN, lo que significa que los mapas de características de las capas ascendentes y descendentes correspondientes de las pirámides se agregan elemento por elemento, y los mapas de abajo hacia arriba se pliegan 1 * 1. Este proceso se muestra esquemáticamente en la Fig. 5.
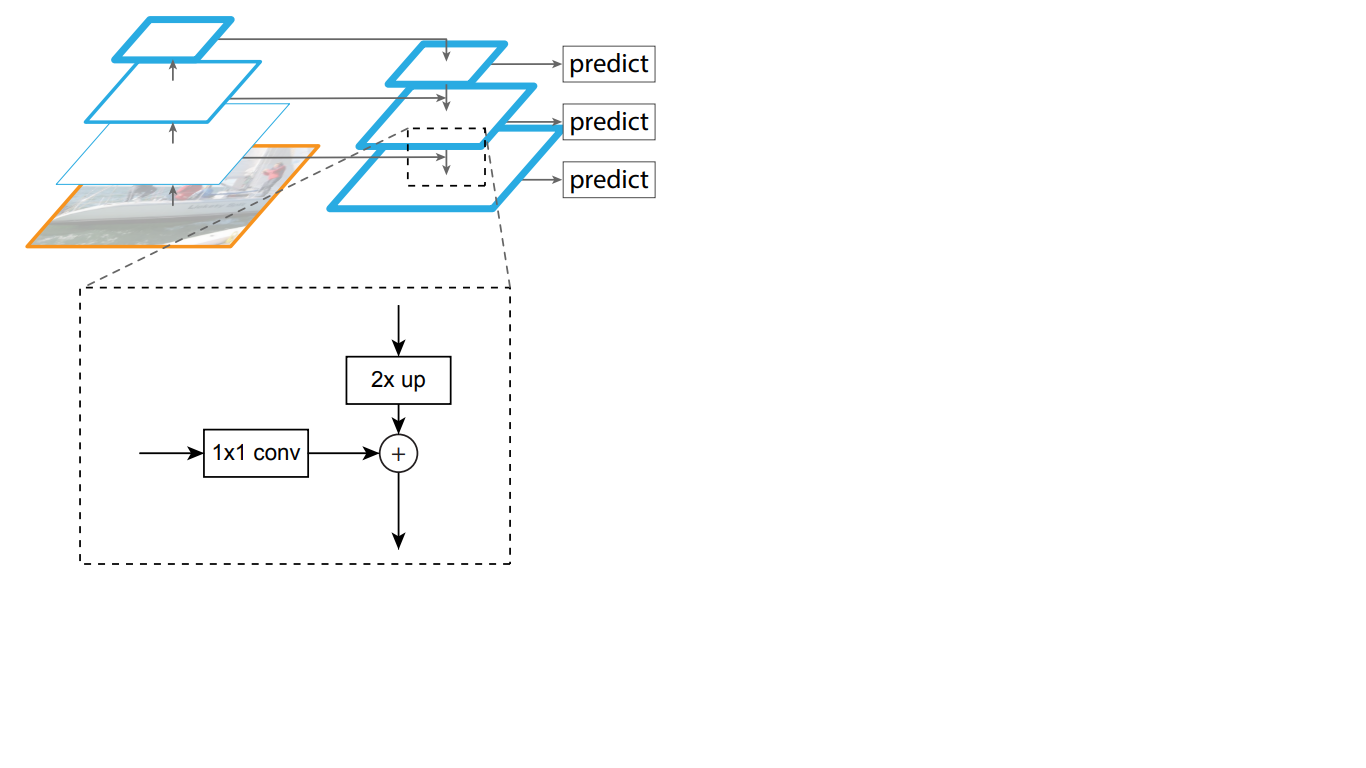
Figura 5 - La estructura de la pirámide de signos
Las conexiones laterales resuelven el problema de la atenuación de señales importantes en el proceso de pasar a través de las capas, combinando información semánticamente importante recibida al final de la primera pirámide e información más detallada obtenida anteriormente en ella.
Además, cada una de las capas resultantes en la pirámide de arriba hacia abajo es procesada por dos subredes.
Subredes de clasificación y regresión
La tercera parte de la arquitectura RetinaNet son dos subredes: clasificación y regresión (Figura 6). Cada una de estas subredes forma en la salida una respuesta sobre la clase del objeto y su ubicación en la imagen. Consideremos cómo funciona cada uno de ellos.

Figura 6 - Subredes de RetinaNet
La diferencia en los principios de los bloques considerados (subredes) no difiere hasta la última capa. Cada uno de ellos consta de 4 capas de redes convolucionales. 256 mapas de características se forman en la capa. En la quinta capa, el número de mapas de características cambia: la subred de regresión tiene mapas de características 4 * A, la subred de clasificación tiene mapas de características K * A, donde A es el número de cuadros de anclaje (descripción detallada de los cuadros de anclaje en la siguiente subsección), K es el número de clases de objetos.
En la última, sexta capa, cada mapa de características se transforma en un conjunto de vectores. El modelo de regresión en la salida tiene para cada cuadro de anclaje un vector de 4 valores que indican el desplazamiento del cuadro de verdad del terreno en relación con el cuadro de anclaje. El modelo de clasificación tiene un vector caliente de longitud K en la salida para cada marco de anclaje, en el que el índice con el valor 1 corresponde al número de clase que la red neuronal asignó al objeto.
Marcos de anclaje
En la última sección, se utilizó el término marcos de anclaje. Anchor box es un hiperparámetro de detectores de redes neuronales, un rectángulo delimitador predefinido con respecto al cual opera la red.
Digamos que la red tiene un mapa de características 3 * 3 en la salida. En RetinaNet, cada celda tiene 9 cajas de anclaje, cada una con un tamaño y una relación de aspecto diferentes (Figura 7). Durante el entrenamiento, los marcos de anclaje se corresponden con cada marco objetivo. Si su indicador IoU tiene un valor de 0.5, entonces el marco de anclaje se asigna como objetivo, si el valor es menor a 0.4, entonces se considera el fondo, en otros casos el marco de anclaje será ignorado para el entrenamiento. La red de clasificación se entrena en relación con la asignación (clase de objeto o fondo), la red de regresión se entrena en relación con las coordenadas del marco de anclaje (es importante tener en cuenta que el error se calcula en relación con el marco de anclaje, pero no con el marco objetivo).
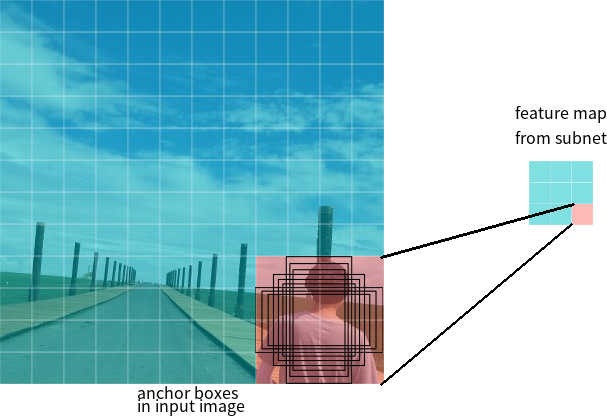
Figura 7 - Marcos de anclaje para una celda del mapa de características con un tamaño de 3 * 3
Funciones de pérdida
Las pérdidas de RetinaNet son compuestas, están compuestas de dos valores: el error de regresión o localización (denotado como Lloc a continuación) y el error de clasificación (denotado como Lcls a continuación). La función de pérdida general se puede escribir como:
Donde λ es un hiperparámetro que controla el equilibrio entre las dos pérdidas.
Consideremos con más detalle el cálculo de cada una de las pérdidas.
Como se describió anteriormente, a cada marco objetivo se le asigna un ancla. Denotemos estos pares como (Ai, Gi) i = 1, ... N, donde A representa el ancla, G es el marco objetivo y N es el número de pares coincidentes.
Para cada ancla, la red de regresión predice 4 números, que se pueden denotar como Pi = (Pix, Piy, Piw, Pih). Los primeros dos pares representan la diferencia predicha entre las coordenadas de los centros del anclaje Ai y el marco objetivo Gi, y los dos últimos representan la diferencia predicha entre su ancho y alto. En consecuencia, para cada marco objetivo, Ti se calcula como la diferencia entre los marcos ancla y objetivo:
Donde smoothL1 (x) se define mediante la siguiente fórmula:
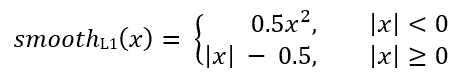
La pérdida del problema de clasificación de RetinaNet se calcula utilizando la función de pérdida focal.
donde K es el número de clases, yi es el valor objetivo de la clase, p es la probabilidad de predecir la i-ésima clase, γ es el parámetro de enfoque, α es el coeficiente de sesgo. Esta característica es una característica avanzada de entropía cruzada. La diferencia radica en la adición del parámetro γ∈ (0, + ∞), que resuelve el problema del desequilibrio de clases. Durante el entrenamiento, la mayoría de los objetos procesados por el clasificador son el fondo, que es una clase separada. Por lo tanto, puede surgir un problema cuando la red neuronal aprende a determinar el fondo mejor que otros objetos. La adición de un nuevo parámetro resolvió este problema al reducir el valor de error para los objetos fácilmente clasificados. Los gráficos de las funciones de entropía focal y cruzada se muestran en la figura 8.
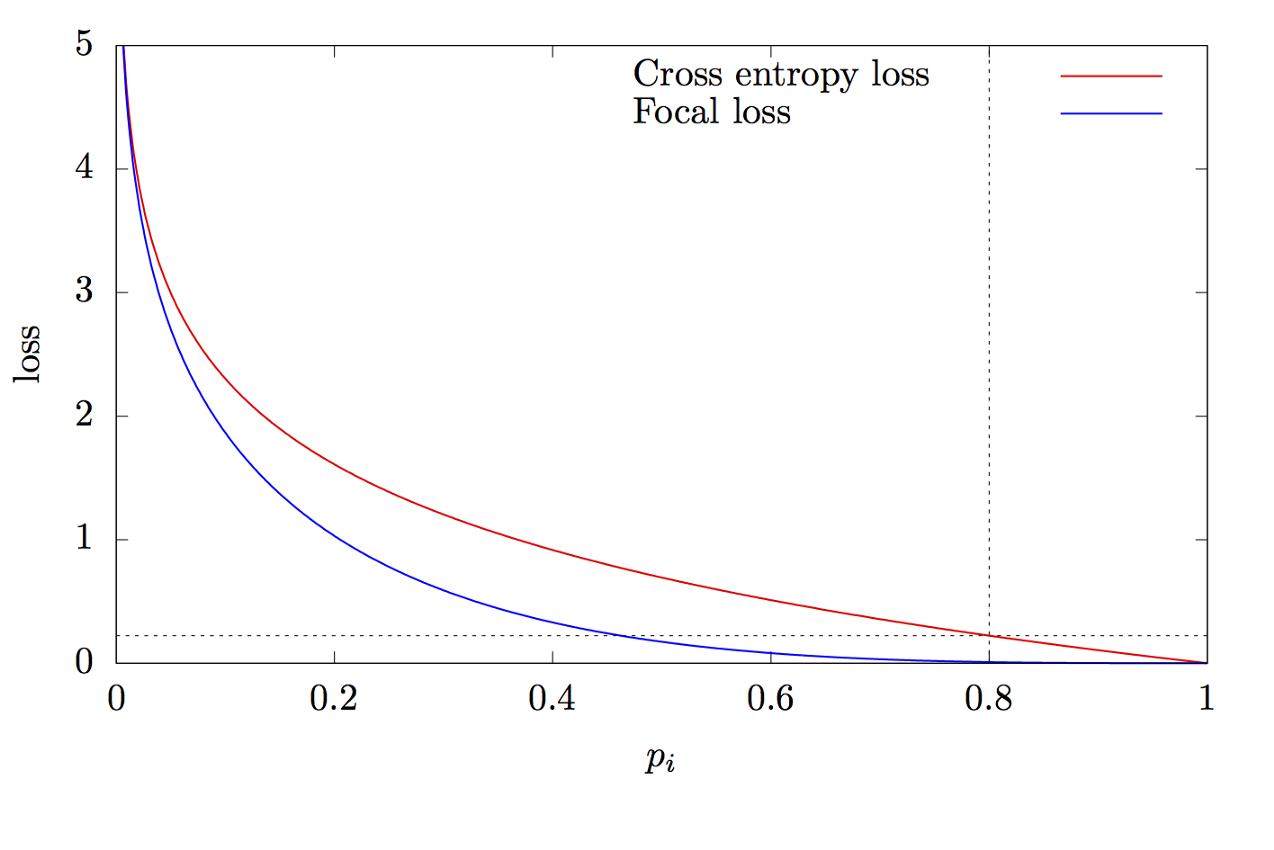
Figura 8 - Gráficos de funciones de entropía focal y cruzada
¡Gracias por leer este artículo!
Lista de fuentes:
- Tan M., Le Q. V. EfficientNet: Rethinking Model Scaling for Convolutional Neural Networks. 2019. URL: arxiv.org/abs/1905.11946
- Zeng N. RetinaNet Explained and Demystified [ ]. 2018 URL: blog.zenggyu.com/en/post/2018-12-05/retinanet-explained-and-demystified
- Review: RetinaNet — Focal Loss (Object Detection) [ ]. 2019 URL: towardsdatascience.com/review-retinanet-focal-loss-object-detection-38fba6afabe4
- Tsung-Yi Lin Focal Loss for Dense Object Detection. 2017. URL: arxiv.org/abs/1708.02002
- The intuition behind RetinaNet [ ]. 2018 URL: medium.com/@14prakash/the-intuition-behind-retinanet-eb636755607d