Clever Geek Handbook

La paradoja del cumpleaños en los datos de VK

¡Hola!



Decidí verificar la paradoja del cumpleaños usando los datos disponibles de VK.



¿Cuál es la paradoja del cumpleaños?



Intente responder la pregunta: ¿Cuántas personas en una habitación se necesitan para que dos personas tengan el mismo cumpleaños con una probabilidad de 0.5? (fecha y mes). La paradoja del cumpleaños responde a esta pregunta.



Para resolver el problema, vale la pena resaltar varios requisitos previos:



  1. El modelo no tendrá 29 de febrero => 365 días al año en el modelo
  2. Cada uno de los 365 días es igualmente probable.


Por supuesto, no es del todo realista que los cumpleaños sean igualmente probables: hay efectos estacionales que afectan las fechas de nacimiento de los niños, creo que usted mismo puede adivinar qué ...



La mayoría de las personas responden intuitivamente la pregunta del problema: 180. Parece lógico, se necesitan 180 personas para tener probabilidad de 0.5 cumpleaños idénticos (365 días en total). Todos los que nunca han oído hablar de la paradoja del cumpleaños tratan sobre esta intuición. La respuesta correcta es en realidad mucho menos que 180, e incluso 150, e incluso 100: 23.



Se requiere al menos 1 cumpleaños coincidente, por lo que puedo encontrar la probabilidad de que no haya cumpleaños coincidentes:

P(" ")=365∗364∗363∗...∗(365−k+1)365k=365!365k∗(365−k)!

...

La idea es esta: tomo a la primera persona y recuerdo su cumpleaños, luego la segunda y calculo la probabilidad de que su cumpleaños no coincida con el cumpleaños de la primera; más allá del tercero y calculo la probabilidad de que su cumpleaños no coincida con los cumpleaños del primero y segundo.



Al resolver la ecuación, resulta que se necesitan 23 personas y la probabilidad de cumpleaños coincidentes será 0.5073, con 100 personas, la probabilidad es 0.9999.



¿Veamos la paradoja sobre los datos de VK?



En teoría, con 23 personas, la probabilidad de cumpleaños coincidentes es 0.5073, con 50 personas 0.97 y con 100 0.99. Vamos a verlo a través de la API de VK.



1. Elijo una gran comunidad en VK. Decidí tomar el grupo MDK en Vkontakte ...



Primero, creo un archivo csv con las columnas que necesito. 



with open('vk_data.csv', 'w') as new_file:
                # csv
                fieldnames = ['id', 'bdate', 'bmonth', 'byear', 'dandm']

                csv_writer = csv.DictWriter(new_file, fieldnames=fieldnames, delimiter=',')

                csv_writer.writeheader()

                newDict = dict()


Me conecto a VK a través de la API y configuro el público que necesito 

vk_session = vk_api.VkApi('username', 'password')
                vk_session.auth()

                vk = vk_session.get_api()
                
                vk_group = vk.groups.getMembers(group_id = 'mudakoff', fields = 'bdate')


Comenzamos a analizar VKontakte, su API le permite analizar solo 1000 usuarios, por lo que creo un bucle. 



for i in range(0, 20):
                    vk_group = vk.groups.getMembers(group_id = 'mudakoff', offset = 1000 * i,  fields = 'bdate')
                    for k in range(0, 1000):
                        try:
                            new_file.write(str(vk_group['items'][k]["id"]) + ',' + str(vk_group['items'][k]["bdate"]).replace('.', ','))
                            new_file.write('\n')
                        except:
                            pass


En teoría, asumimos que los cumpleaños son igualmente probables, pero ¿qué sucede en la práctica? Construiré un histograma de cumpleaños.



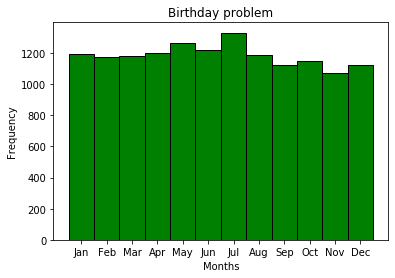
imagen



Los cumpleaños por mes no son eventos equiprobables, lo que generalmente es bastante lógico; este es solo un requisito previo para resolver el problema del cumpleaños. Obviamente, habrá diferentes eventos de temporada, para diferentes lugares. Por alguna razón, julio es el mes más popular para el cumpleaños de los suscriptores de MDK.



Voy a estimar empíricamente la probabilidad de que en un grupo de 50 personas arbitrarias haya al menos dos con el mismo cumpleaños. Para hacer esto, escribí un ciclo durante el cual se produce una submuestra de 50 líneas de la tabla. Para estas 50 líneas dentro de la condición, verifiqué la coincidencia de cumpleaños. Si coincidía, entonces lo recordaba en la variable del contador, que luego dividiría por la duración del ciclo para obtener la probabilidad. 



fifty = df["dandm"].sample(n = 50)
for i in range(0, 1000):
    fifty = df["dandm"].sample(n = 50)
    for j in fifty.duplicated():
        if j == True:
            counter = counter + 1
            break
print(':', counter / 1000)


La probabilidad se obtiene en la región de 0.97, que coincide con los datos teóricos.



Salida



Fue interesante ver cómo la teoría se relaciona con el empirismo, y en este caso los datos confirman la teoría. Cabe señalar que el resultado es representativo, ya que la muestra es lo suficientemente grande: 20,000 personas.



Recursos



  1. Universidad Harvard. Problema de cumpleaños, propiedades de probabilidad | Estadísticas 110. URL: www.youtube.com/watch?v=LZ5Wergp_PA&t=150s . Acceso: 08/07/2020
  2. Problema de cumpleaños. URL: en.wikipedia.org/wiki/Birthday_problem . Accedido: 07/08/2020>


More articles:


All Articles