- Hola a todos, mi nombre es Rishat. He estado trabajando en la calidad de la búsqueda de Yandex durante casi tres años. Pero hoy quiero hablar no sobre el trabajo, sino sobre lo que hago en mi tiempo libre. Me dedico a la informática cuántica, pero de hecho, una variedad de modelos de computación, incluidos los cuánticos.
La informática cuántica es un área interesante en este momento. Se está invirtiendo mucho esfuerzo allí, se ha hecho mucho. En mi informe intentaré interesar a algunos de ustedes. Tal vez hay un ingeniero de ML genial entre ustedes que quiere hacer aprendizaje automático cuántico, o simplemente un algoritmo fuerte que puede invertir en esta dirección. Será genial porque el futuro llegará pronto.
Debo decir de inmediato que no soy físico. Seguramente hay personas entre ustedes que entienden todos estos procesos en física más que yo. Por lo tanto, no diré casi nada sobre física.
Espero de usted que recuerde un poco el álgebra, recuerde qué es un vector y cómo multiplicar un vector por una matriz.

¿Cómo se estructurará mi informe? Primero, hablaremos un poco sobre la historia, de dónde vino todo para mirar con confianza hacia el futuro. Luego veremos dónde se puede aplicar esto, en qué estado se encuentra ahora, si es posible hacer algo con sus manos en este momento. Vamos a escribir el primer programa Python que se puede ejecutar en una computadora cuántica. Y luego, como beneficio adicional, le mostraré algunos ejemplos de algoritmos en los que la computación cuántica ayuda a lograr un rendimiento incomparablemente mejor en comparación con los clásicos.

¿Cómo empezó todo? De este joven. Este es Alan Turing, se le puede llamar con seguridad el padre de la informática o la informática, por la cual todos vivimos ahora, ganar dinero. En la década de 1930, a Turing se le ocurrió un modelo de computación que ahora llamaríamos una computadora programable. ¿Pero alguien reconocerá a esta persona?

Más difícil. Su apellido muy a menudo va junto al apellido de Turing. Esta es Alonzo Church, también se ocupó de problemas de computabilidad, e incluso un poco antes de que Turing presentara sus propios modelos de computación. Pero el trabajo de Turing se hizo más popular. Y en general, Church en algún momento fue el asesor científico de Turing. En conjunto, sus nombres generalmente están asociados con esta tesis.
La tesis de Church-Turing dice: cualquier proceso puede ser modelado eficientemente en una máquina de Turing. Esto es a finales de los 30, principios de los 40, y todo está muy bien. Durante unos 30 años todo está muy bien, hasta que aparecieron estas dos personas. ¿Alguien los conoce?

Esto ya es los años 70, muy cerca del presente. Sus apellidos se encuentran a menudo en cursos de criptografía. Estos son Robert Nightingale y Volker Strassen. Estas dos personas son famosas por idear un algoritmo probabilístico para verificar la simplicidad de un número, la prueba Solovey-Strassen.
Y este es un punto muy importante para nosotros, porque hasta ahora dijimos que cualquier proceso algorítmico se puede modelar en una máquina Turing. Pero ahora resulta que su algoritmo no puede ser modelado. Es probabilístico, no hay nada de eso en la máquina de Turing.
Tuve que hacer una solución rápida y decir que cualquier proceso puede ser modelado en una máquina de Turing probabilística. Esto ya no es muy bueno, seguro que uno de ustedes tiene un pellizco en el pecho. Pensaste: ¿cómo es eso? Ahora decimos "probabilístico", en diez años se descubrirá algo más, habrá que corregir algo más. Esto no es muy agradable. Pero tú y yo, por supuesto, no estamos solos.

Había otro joven, David Deutsch. Y él también se preguntó: ¿cómo es eso? ¿Como vivir? Es físico de formación, dedicó toda su vida a la física. Y decidí abordar este problema desde el punto de vista de la física. Él dijo: tratemos de corroborar, obtener algo para que la naturaleza misma nos diga que este es exactamente el caso. Y la naturaleza ya dijo entonces (y todavía creemos) que es mecánica cuántica. Entonces comenzamos a buscar una respuesta en mecánica cuántica. Y fue con David Deutsch, con sus primeros algoritmos, que comenzó la informática cuántica.
Esta es una pequeña excursión a la historia para que entiendan: no salió de la nada. En esta área hay problemas reales, teóricos, por supuesto, que atormentan a las personas que lo comenzaron todo.
¿Pero todo está solo en el nivel de la teoría? En general, desde el punto de vista de las matemáticas, no quedan problemas. Matemáticamente, sabemos todo sobre cómo debería funcionar una computadora cuántica. Ahora ya hay computadoras cuánticas reales de diferentes configuraciones, que funcionan de diferentes maneras. Y esto es, en general, un desafío de ingeniería.
Por ejemplo, en nuestro instituto tenemos un departamento completo que se ocupa de la informática cuántica. Hay matemáticos y físicos. Los físicos ahora están muy involucrados en el problema del almacenamiento a largo plazo de información cuántica. Es muy similar a nuestros discos duros, pero queremos que la información cuántica se almacene allí.

¿Cuáles son los usos de toda esta economía? Por supuesto, lo primero que viene a la mente es el modelado de procesos, porque el mundo es de mecánica cuántica. Y si usamos una computadora cuántica para simular procesos, reacciones químicas o lo que sea, será mucho más barato computacionalmente.
La segunda sección, muy grande, a la que ahora se dedican muchos esfuerzos, es el aprendizaje automático cuántico. Existe una gran esperanza de que la computación cuántica ayude a acelerar los procesos de aprendizaje y a mejorar los algoritmos. Hay mucho trabajo aquí. Ahora, por ejemplo, nuestro grupo cuántico está trabajando junto con un científico de China. Él es un ingeniero de ML muy fuerte, y tenemos un sesgo cuántico, tratando de llegar a algo juntos.
La tercera cosa fue un poco exagerada hace unos meses. Ahora, tal vez el bombo ya está dormido, pero incluso hay una cadena de bloques cuántica completa. Fue inventado por mi buen amigo y gran amigo. Este soy yo, digo con orgullo.
Pero no tenemos una computadora cuántica. Desafortunadamente, no podemos volver a casa y ejecutar programas tan fácilmente como programamos en Python.
¿Qué hacer? Estaba pensando en qué hacer en mi tercer año cuando estaba escribiendo mi primer trabajo. Estaba escribiendo un emulador de computación cuántica. Por supuesto, todos escriben emuladores y todos los usan de alguna manera. En mi cuarto año, escribí un emulador que simula interferencias, ruidos, etc. Y luego me aburrí.
Traté de buscar en un motor de búsqueda y me di cuenta de que hay muchos emuladores. Aquí hay algunos enlaces, son bastante simples e interesantes:
- github.com/quantumlib/Cirq
- github.com/artiste-qb-net/qubiter
- code.google.com/archive/p/pyqu
- qiskit.org
Pero quiero parar en qiskit. Es especial, se destaca de todos. ¿Que?
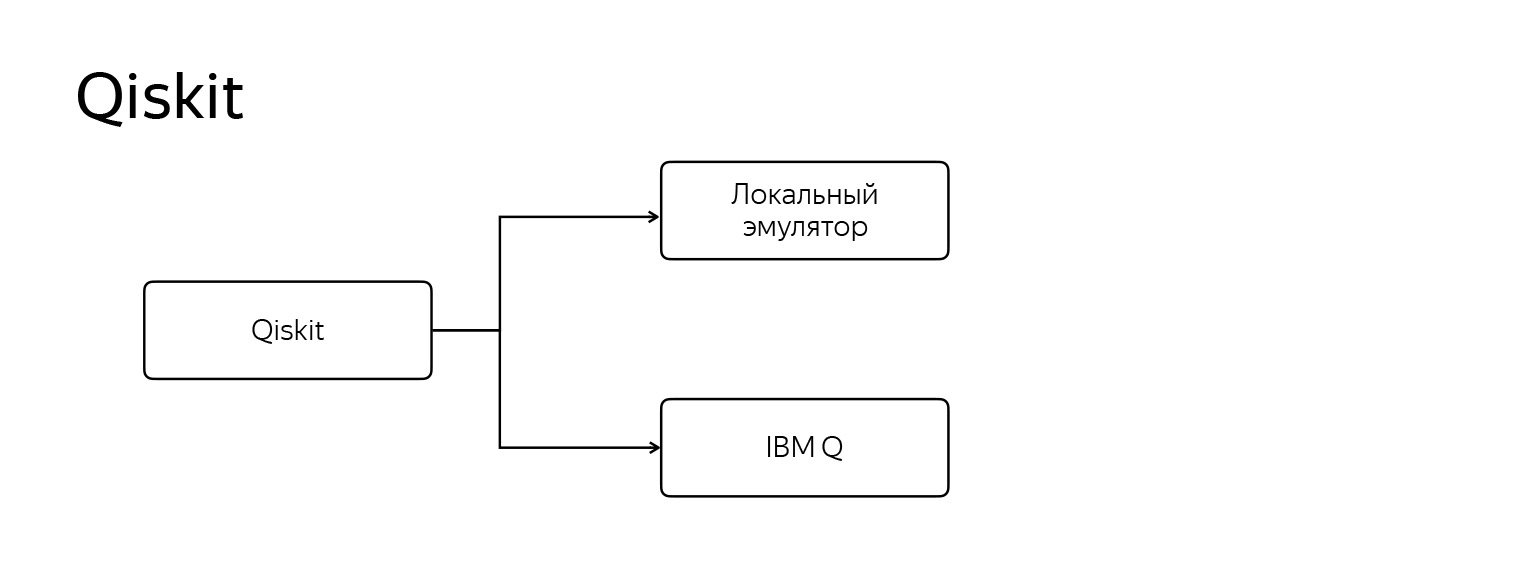
Funciona en dos modos. El primero es, como todos los demás, un emulador local regular. El segundo es ejecutar su programa en una computadora cuántica IBM Q real, que se parece a esto.

Ahora es un barril entero en el que se mantiene una temperatura extremadamente baja, aproximadamente tres milikelvin. Hace mucho frío. E IBM proporciona la capacidad basada en la nube para conectar y ejecutar su código directamente en esa máquina.
Por supuesto, compila comandos y demás de una manera especial. ¿Cómo funciona? Hay varias instalaciones de tal computadora para acceso general. Uno de ellos es de 5 qubits, hay 15 qubits, 16 qubits, incluso 20 qubits están disponibles para nosotros. Esto es aproximadamente 20 bits de información ordinaria, clásica, pero ya algo.
Aquí, seguro, muchos de ustedes piensan: eso es, ¡quiero! Pero tienes que recordar un poco de matemática. Un poco de álgebra, pero solo un poco, como prometí.
Para comenzar a programar en una computadora cuántica, debe comprender qué es un qubit. Es solo un vector en un espacio vectorial 2D. Pero como estamos hablando de espacios vectoriales, tienen una base.

La base se parece a esto. Hay dos columnas de vectores y una base de unidad, estándar, en cursos de álgebra se denota de la siguiente manera:
y
... Y hay una notación estándar en la notación de Dirac, en estos corchetes angulares.
Es decir, para que no te confundas, continuaré acortando así.
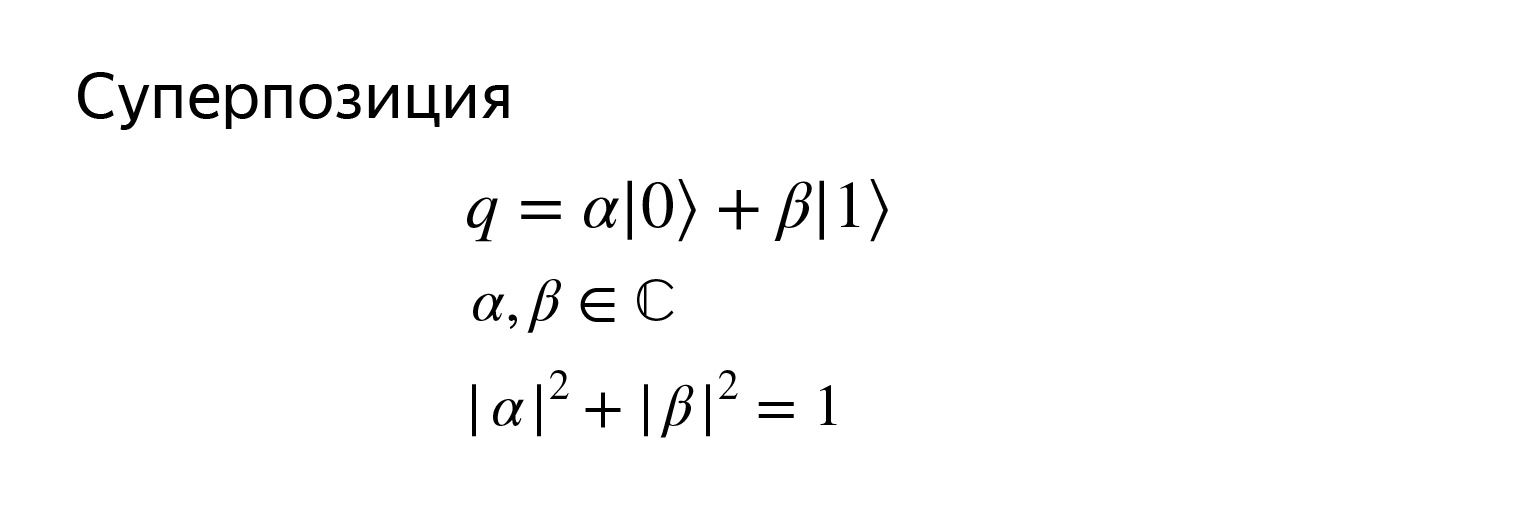
Y como es un vector, su estado puede escribirse así. Un qubit q es una superposición de dos vectores básicos, donde α y β son números complejos, pero no absolutamente ningún número, sino que la suma de los módulos de sus cuadrados es igual a uno.
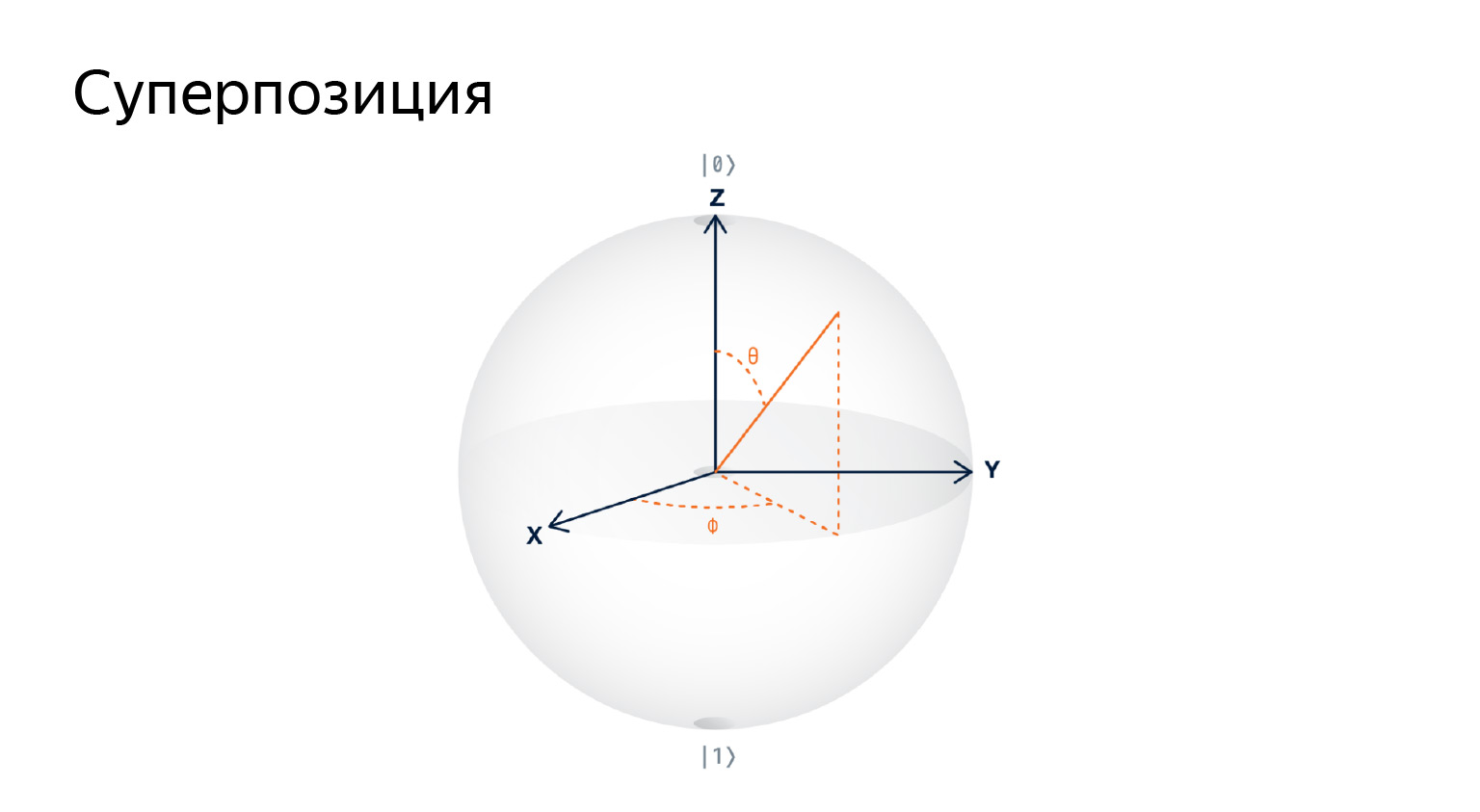
Si tratamos de dibujar esto, obtenemos que un qubit es un vector en una esfera tridimensional. Se puede almacenar una cantidad infinita de información en un qubit, porque es solo un vector, del cual hay una cantidad infinita.
No necesita prestar atención a la imagen, es solo una técnica de visualización para atraer la atención.
Hablamos de qubits. Lo más importante, un qubit es un vector. Vector en espacio vectorial complejo. ¿Qué puedes hacer con eso?
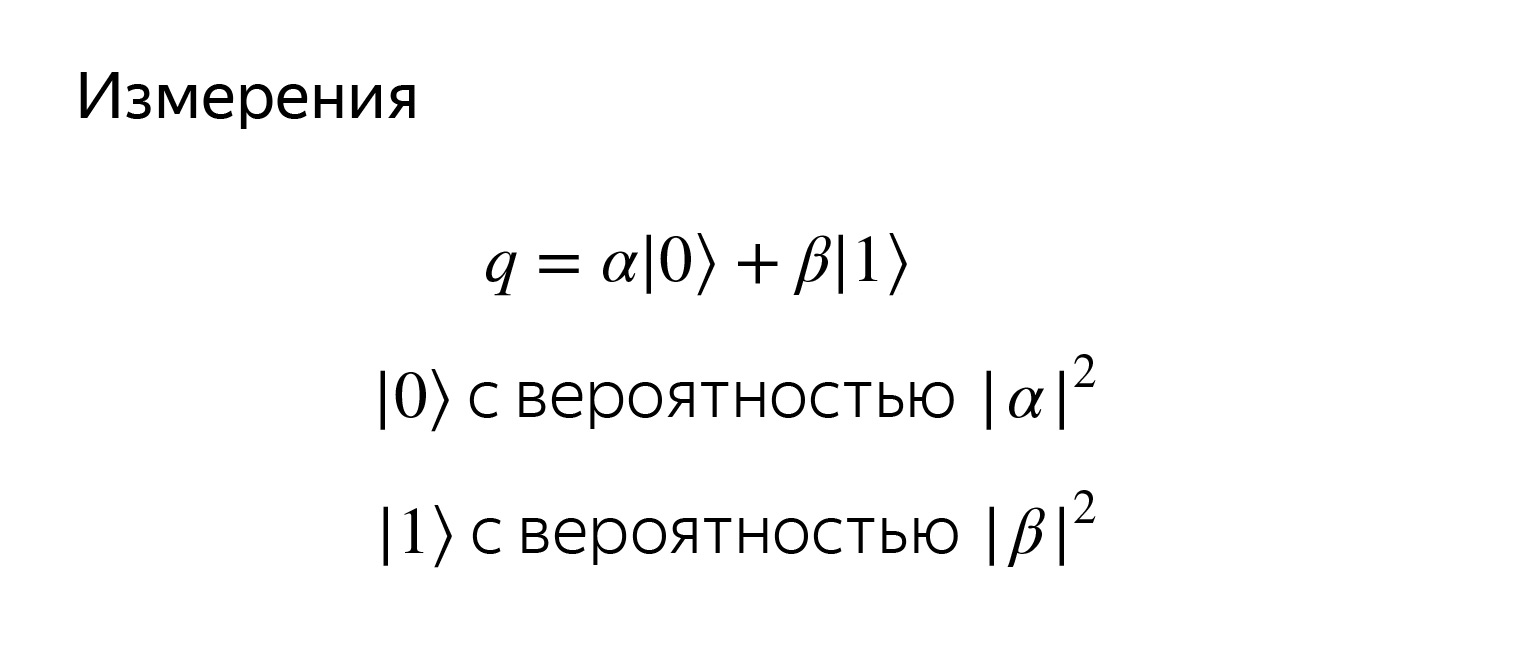
Lo primero que solíamos hacer es tratar de calcular el valor de nuestra variable, por ejemplo, en Python. Queremos leer en qué estado se encuentra el qubit. Pero nunca sabremos el significado exacto de α y β.
Si tratamos de ver un qubit, léelo, entonces obtenemos un cero o uno con las probabilidades correspondientes. Las probabilidades son simplemente proyecciones sobre los vectores de base correspondientes.
La segunda cosa que podemos hacer es, por ejemplo, clonar un qubit. Llamamos a esto asignar una variable a otra. Desafortunadamente, esto no se puede hacer en el mundo cuántico.

No hay una operación de asignación, y esto está muy relacionado con lo que acabo de decir: ni siquiera podremos ver el valor exacto. Este es un resultado fundamental. Se demuestra de manera muy simple : literalmente dos líneas de comparaciones, por contradicción.
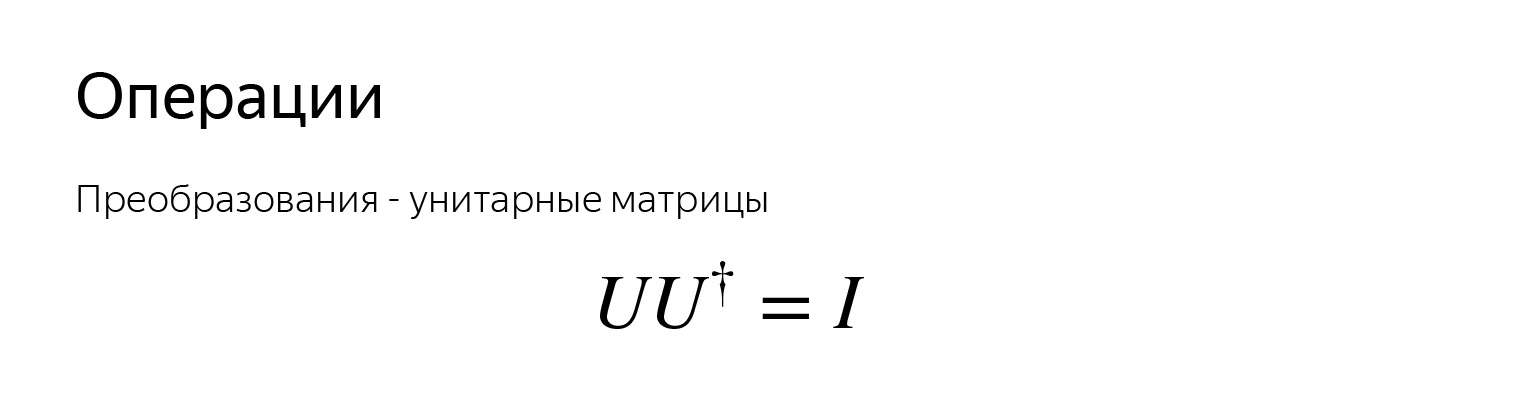
Hay un qubit que no podemos leer, no podemos clonar. ¿Qué puedes hacer en absoluto?
Un qubit es un vector. El vector se puede tomar y rotar alrededor de la esfera. Para rotar, puedes pensar en una matriz que haga esta rotación. Todas las operaciones en qubits son matrices. Se llaman unitarios.
Unitario: para que se cumpla dicha condición, está escrito aquí de una manera astuta. Este icono denota una matriz conjugada transpuesta y compleja. Esta propiedad es muy importante, significa que hay una inversa para cualquier operación. Es decir, no importa cómo giremos el vector, siempre podemos devolverlo a su posición anterior. Siempre hay una operación inversa.
Veamos qué operaciones pueden ser. A lo que estamos acostumbrados en el caso clásico. Hay un cero, puedes convertirlo en uno y viceversa.
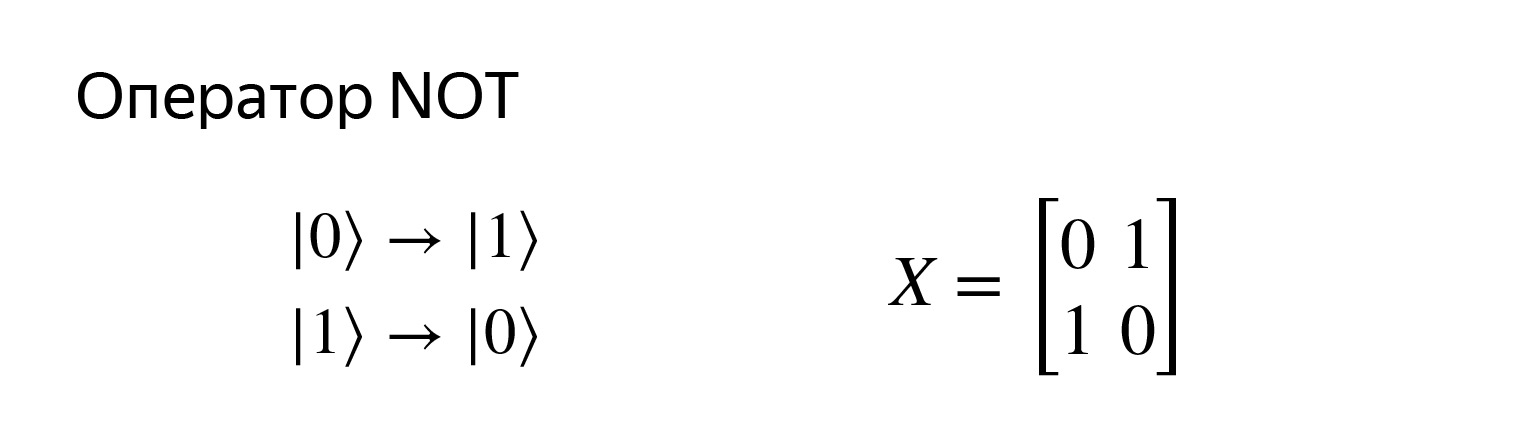
Este es el operador de negación y es muy simple. Se registra con tal matriz. Si tratamos de multiplicar, obtenemos exactamente lo que queremos.
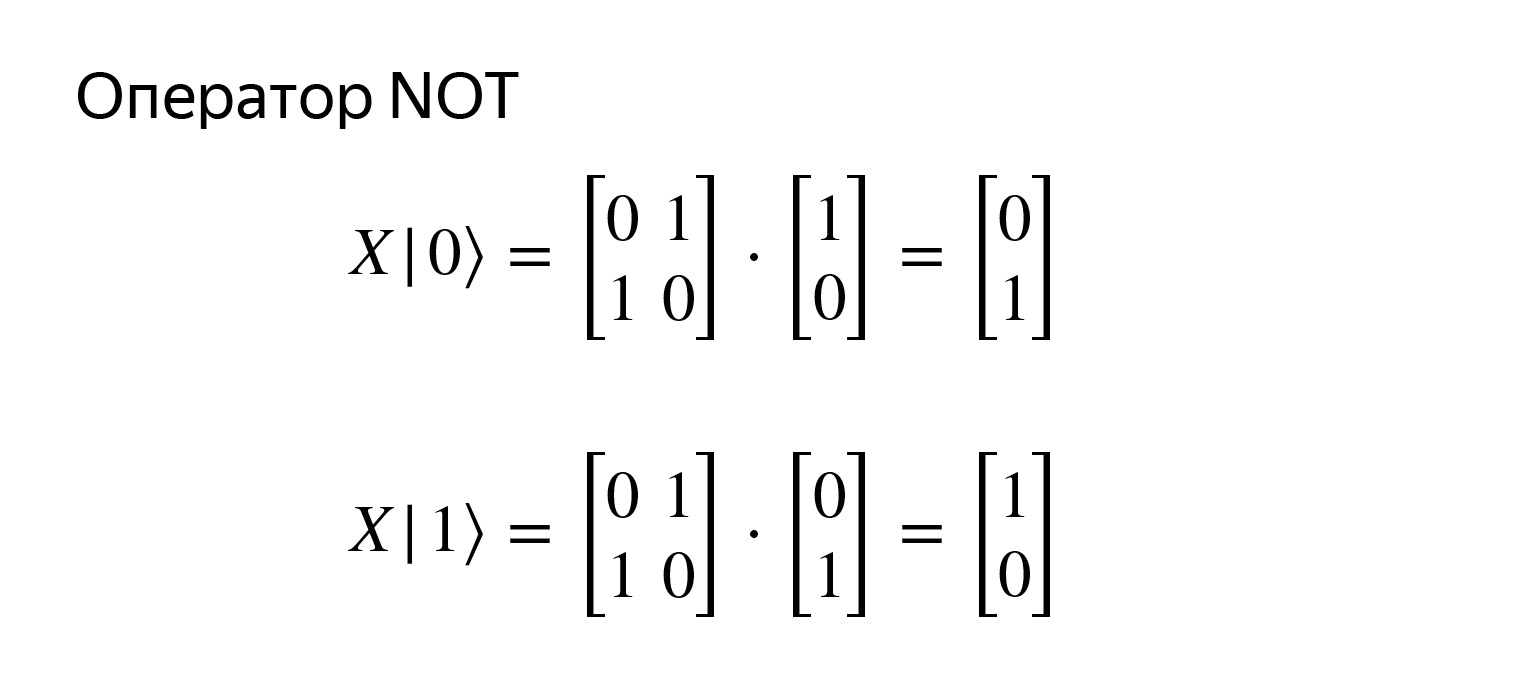
Incluso lo tengo dibujado aquí. Nada complicado El operador de negación tiene una notación estándar, el operador X. Ahora que lo pienso, es solo una rotación alrededor de uno de los ejes. Y hay operadores Y y Z, rotación alrededor de otros ejes, pero esto no es tan importante ahora.
Y ya podemos ejecutar nuestro primer programa en una computadora cuántica que negará un qubit.
Pero nosotros en informática cuántica, por supuesto, rara vez escribimos en Python. Usamos esquemas con más frecuencia.

El diagrama generalmente se ve así. Las líneas horizontales son simplemente valores qubit. Tengo cinco de ellos dibujados aquí. Y en el bloque, la operación que haremos.
Primer bloque. Aquí se dibuja un dispositivo de medición. Esto significa que solo queremos medir lo que está en el primer qubit.
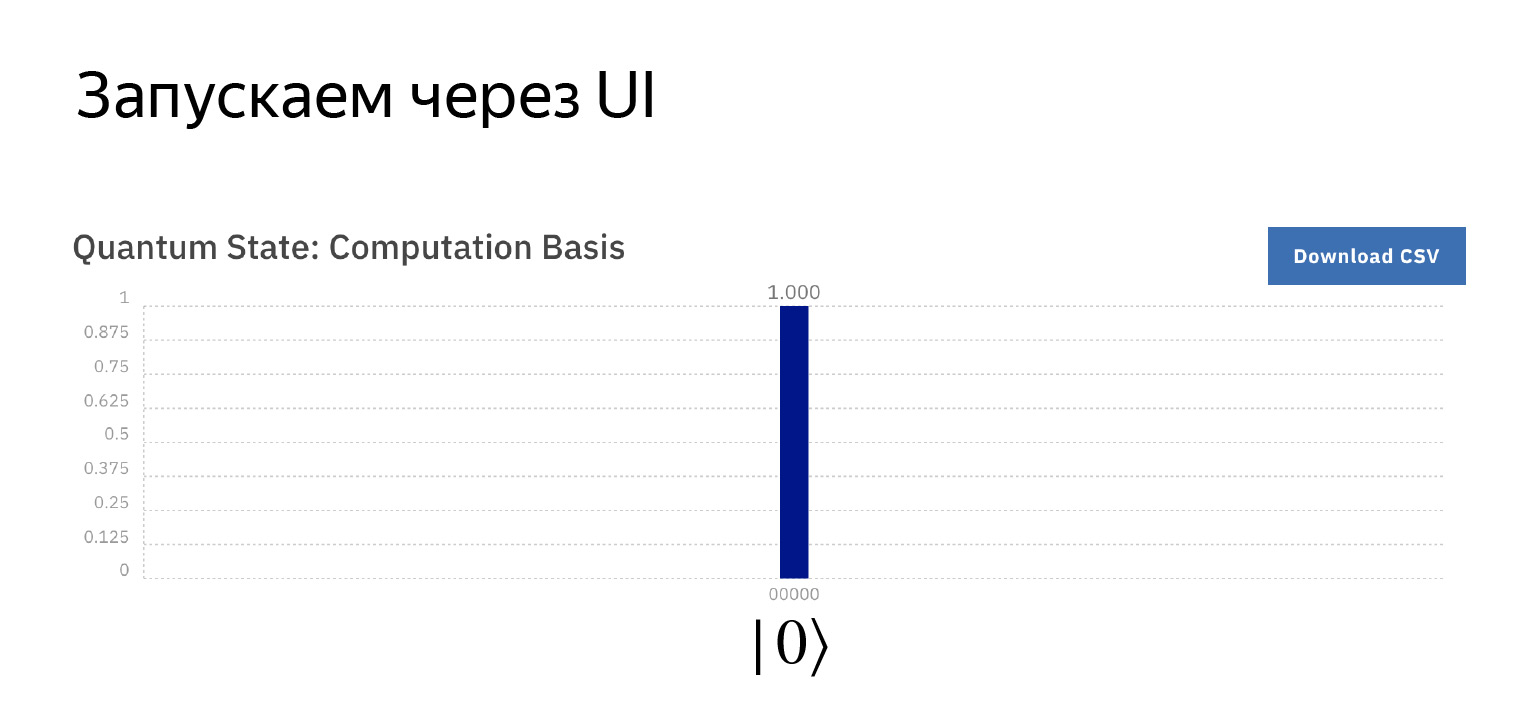
Si ejecutamos esto, obtenemos que con una probabilidad de uno tenemos un cero allí, porque se inicializan en este estado y no hicimos nada más con ellos.
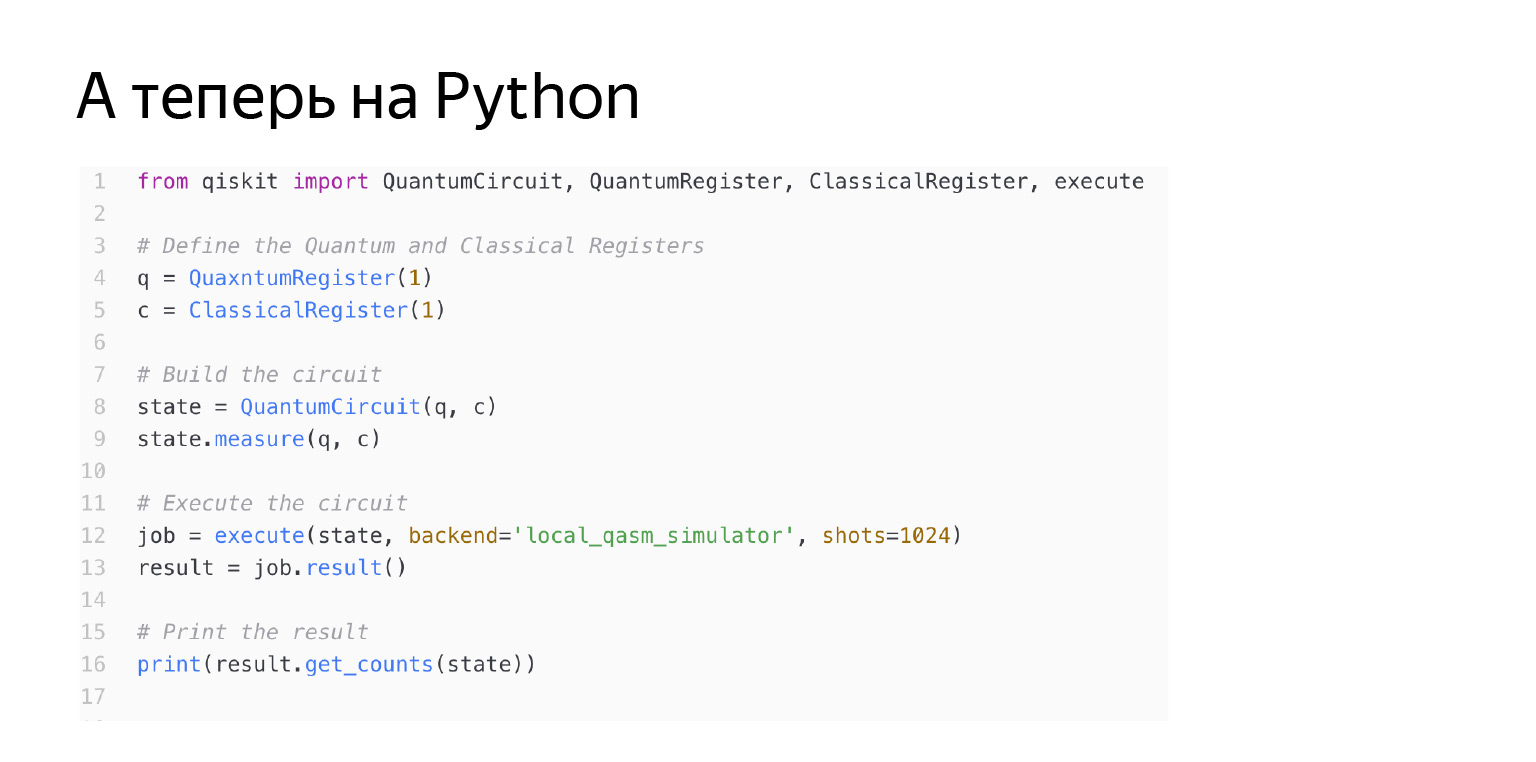
Tal cosa se puede escribir en Python usando la biblioteca qiskit. Veamos qué sucede aquí línea por línea. Primero, comenzamos el registro cuántico. Lo estoy encendiendo aquí desde un qubit. Y el registro clásico. El registro clásico es necesario para escribir el resultado de la medición en alguna parte. Es decir, hago transformaciones con un registro cuántico, el resultado es uno clásico: cero o uno. Y luego creo mi propio circuito, que tiene este qubit clásico cuántico. Solo digo: midamos el q qubit en C. Comencemos todo esto y todo estará bien. Pero el lector atento verá: aquí dice que mi servidor es un emulador local.

Lo mismo se puede hacer con IBM Q, pero hay un poco más de código aquí. Hay todo tipo de fideos sobre la elección de un dispositivo que nos responderá lo antes posible, transfiriendo algunos tokens, eso es todo. Pero no hay nada complicado.

Lo mismo se puede hacer con el operador de negación. Este es el operador X, como dije. Se ve exactamente igual en el diagrama, ejecutemos lo mismo.
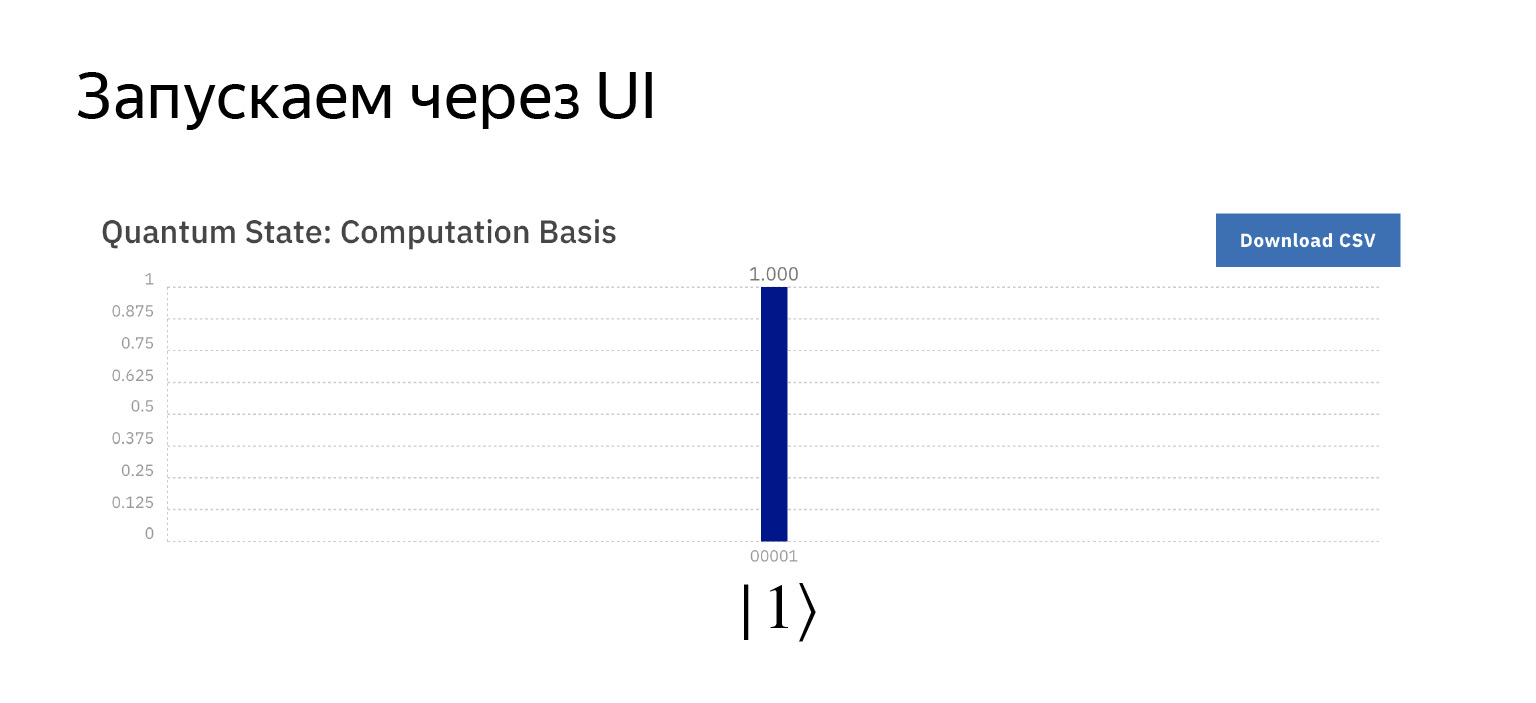
Ahora, con una probabilidad de uno, obtenemos uno, según lo planeado. Sin magia
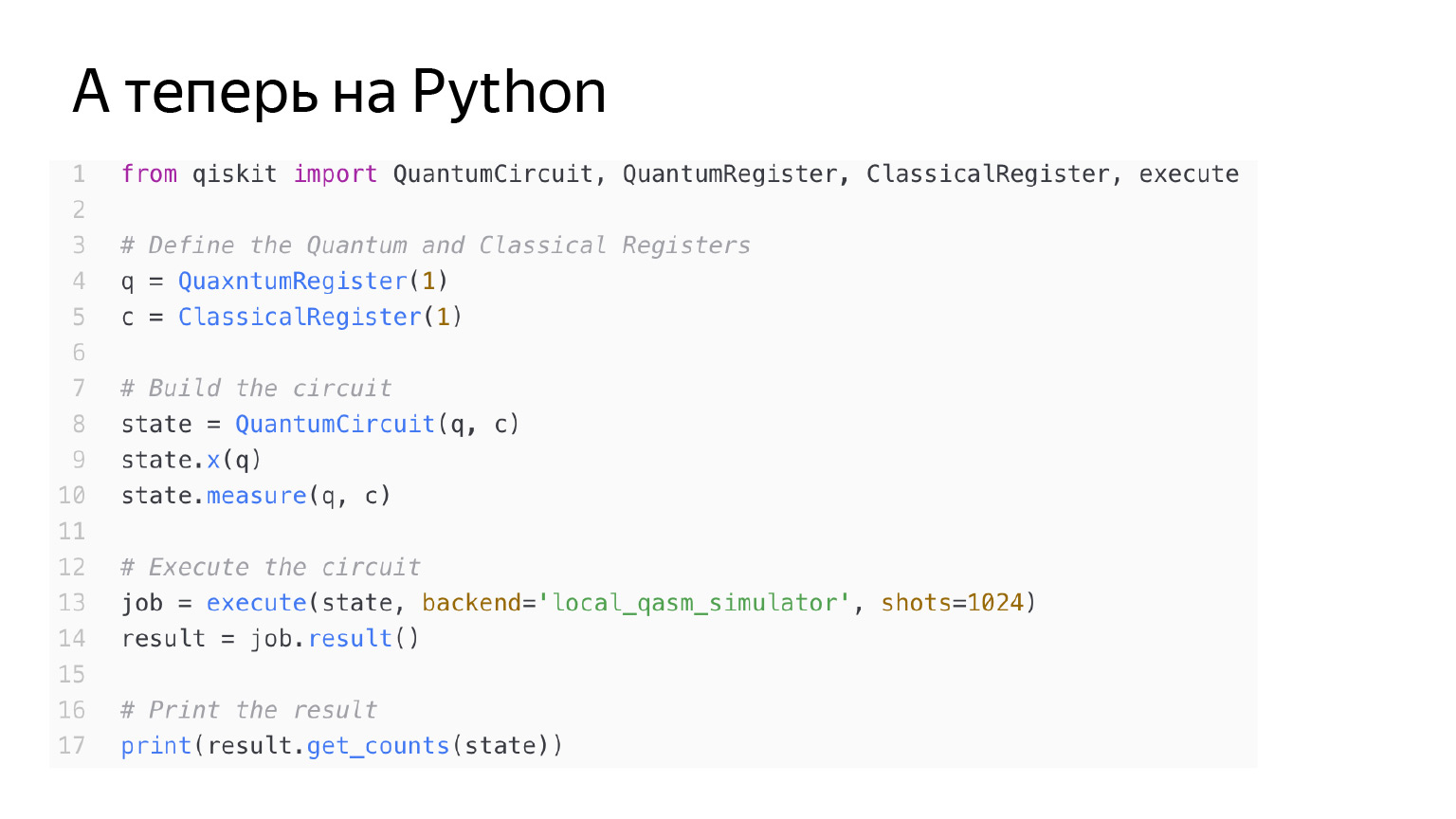
El código es el mismo. Es solo que aquí también estoy aplicando el operador X al q qubit.
Bien, intentemos ir más allá.
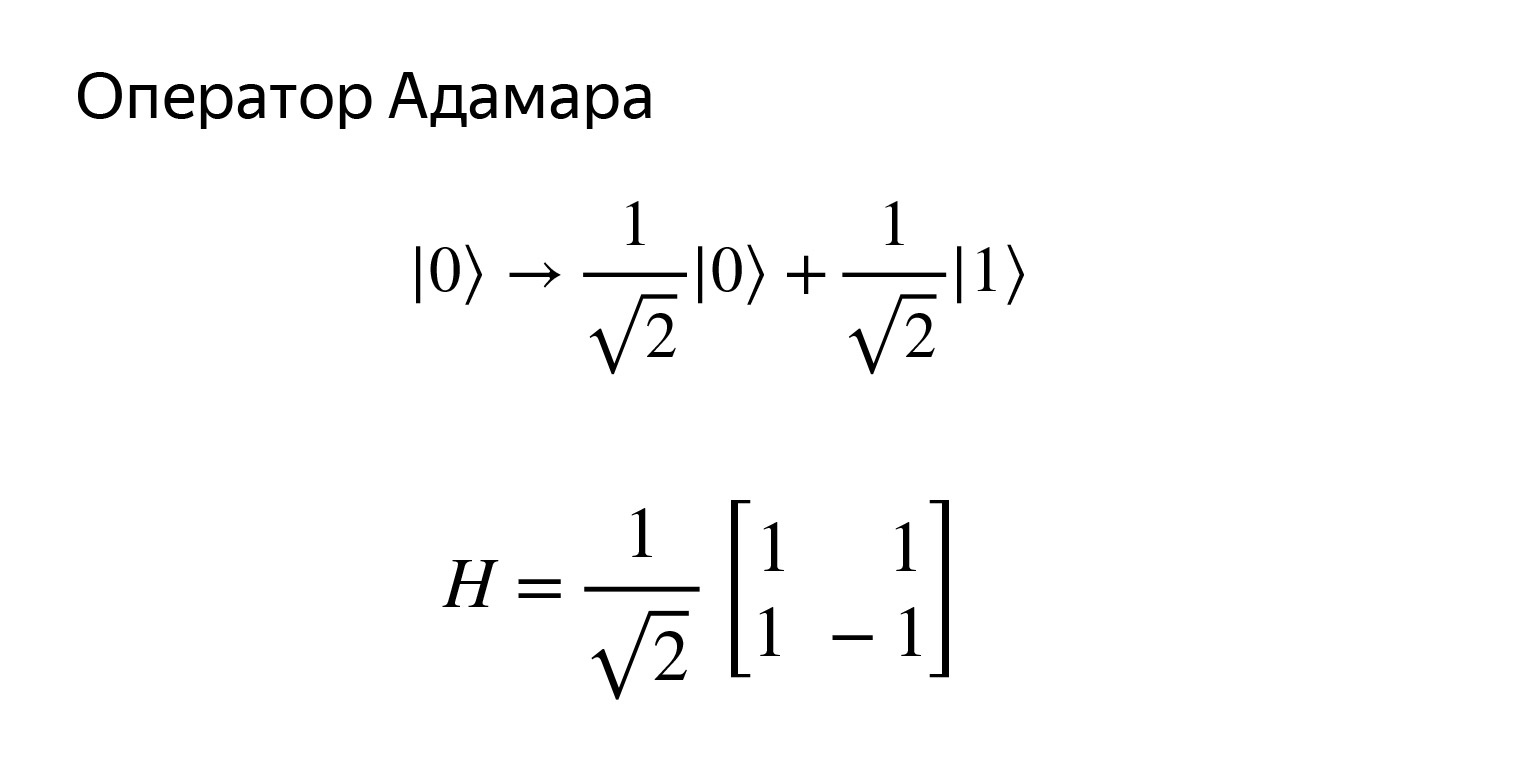
Aquí hay algo muy complicado. Intentemos obtener este estado. Este estado es muy interesante. Obtendremos tal superposición. Si tratamos de medirlo, entonces con una probabilidad de 1/2 obtenemos cero o uno. Es decir, será una superposición tan uniforme, que podemos obtener cualquier cosa.
Se puede establecer una analogía con lo que es un lanzamiento cuántico de monedas. Diremos bien, con probabilidad ½ obtenemos cero y uno. La matriz se ve así.
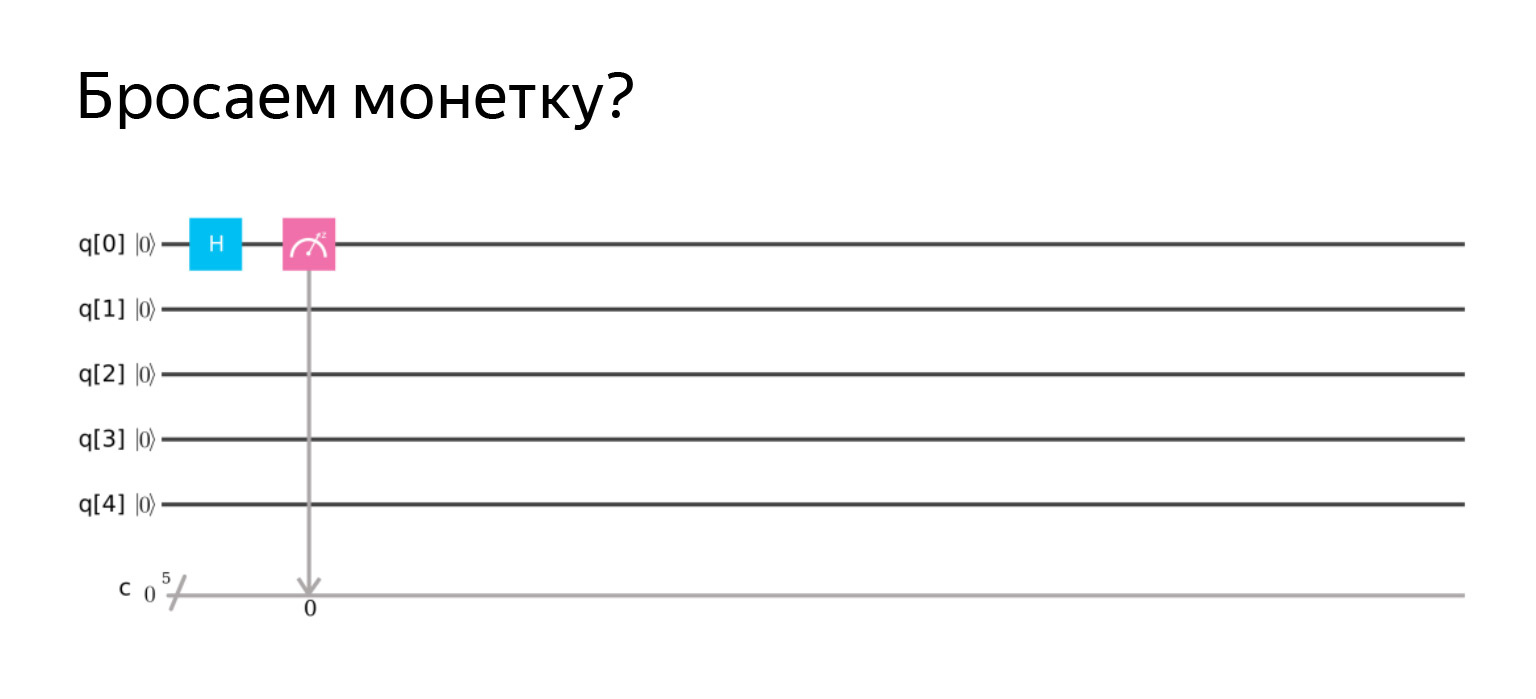
Fácil de verificar, pero ciertamente no lo haremos. Dibujemos un diagrama. Operador H en honor de Hadamard.
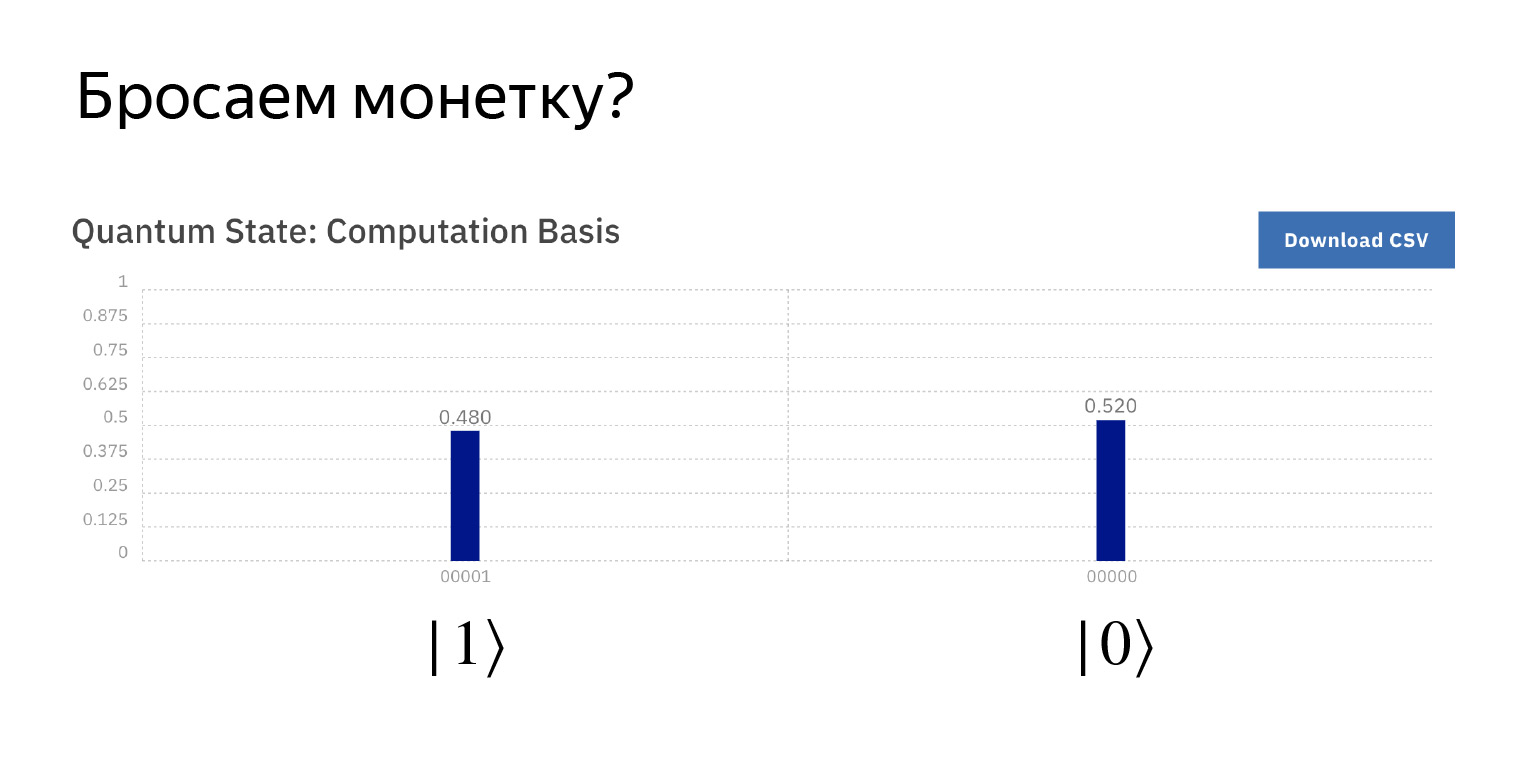
Midamos y obtengamos aproximadamente lo que esperamos. Con una probabilidad de ½, cero y uno. Un poco más, un poco menos, pero así es como funciona.
Aquí está el código de Python, solo para estar allí, estamos en una conferencia de Python.

Existe tal superposición. Le aplicamos el operador Hadamard y lo medimos.
Pero puedes lanzar una moneda dos veces, todos estamos acostumbrados a esto. Si lanzas una moneda dos veces, nada cambia. Intentemos hacer esto en el caso cuántico.

Aplicamos el operador Hadamard dos veces seguidas y siempre obtenemos un cero.

Es decir, si lanza una moneda cuántica dos veces, siempre obtendrá un cero, porque el operador Hadamard es inverso a sí mismo. Si multiplicas por ti mismo, siempre obtienes uno. Aquí hay una cosa.
Entonces, puedes hacer algo con un qubit. Se puede torcer, torcer y medir. Intentemos agregar más qubits. ¿Qué estamos acostumbrados a hacer en el mundo clásico? Tomar y realizar operaciones lógicas simples, "o" y "y".

En el mundo cuántico, no puedes hacer esto, porque no son completamente reversibles. Es decir, al obtener cero en la operación "y", nunca podemos saber cuáles fueron los valores iniciales.
Y en el mundo cuántico, como dije, una operación es una matriz unitaria que siempre es reversible. ¿Cómo, entonces, programa usted? Todo a lo que estamos acostumbrados se está desmoronando. Pero aparece un nuevo héroe, este es el operador de la llamada negación controlada.

Si estuviéramos escribiendo en Python, se vería así. Si el primer qubit es uno, invirtamos el segundo qubit. Esto no es una matriz, así es como se ve el operador. Pero, en principio, lo que dije está escrito aquí. Donde hay unidad en el primer qubit, el segundo se invierte.
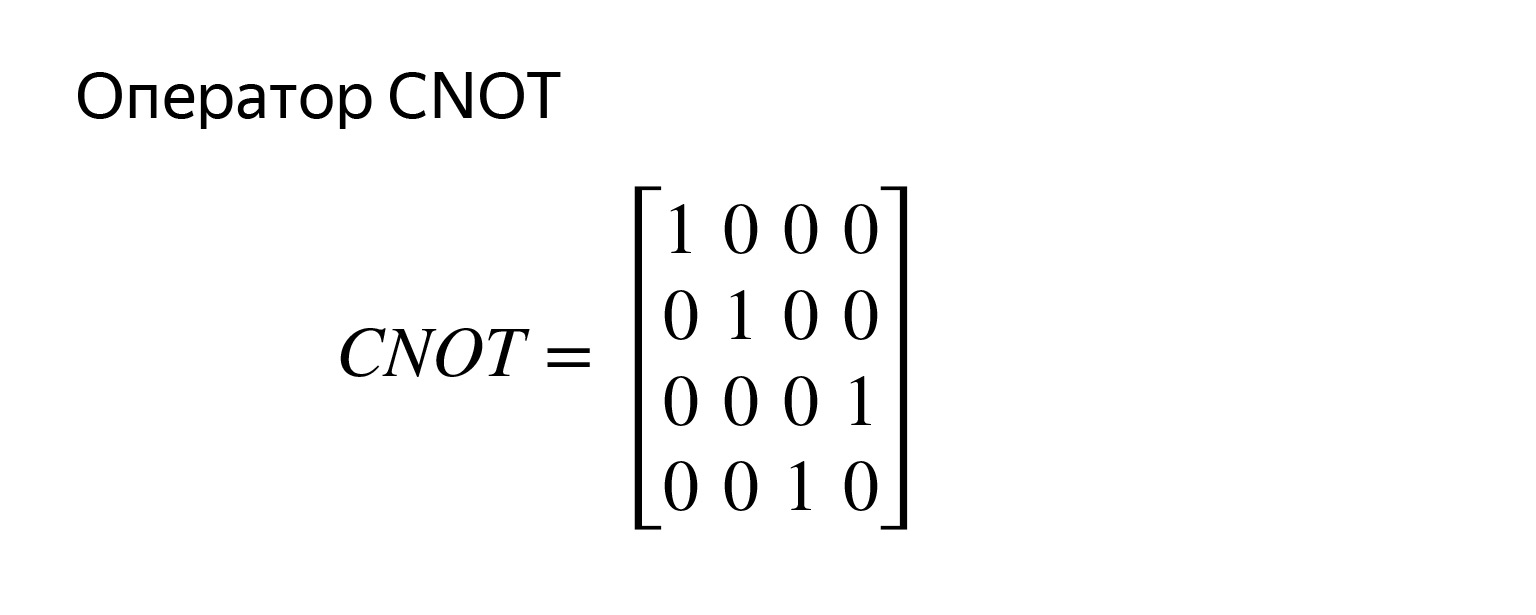
La matriz ya es de cuatro por cuatro. Para dos qubits, se ve así. Dejaré el problema con un asterisco para multiplicar y ver si esto es cierto.

Esta cosa incluso se puede programar. No hay ciencia espacial. Solo necesita tomar, crear un circuito con dos qubits, con dos clásicos, y hacer, no solo CNOT, sino CX, negación controlada.
La negación era el operador X, por lo que, en principio, todo es lógico. Y puedes dibujar un diagrama. El esquema es el siguiente.
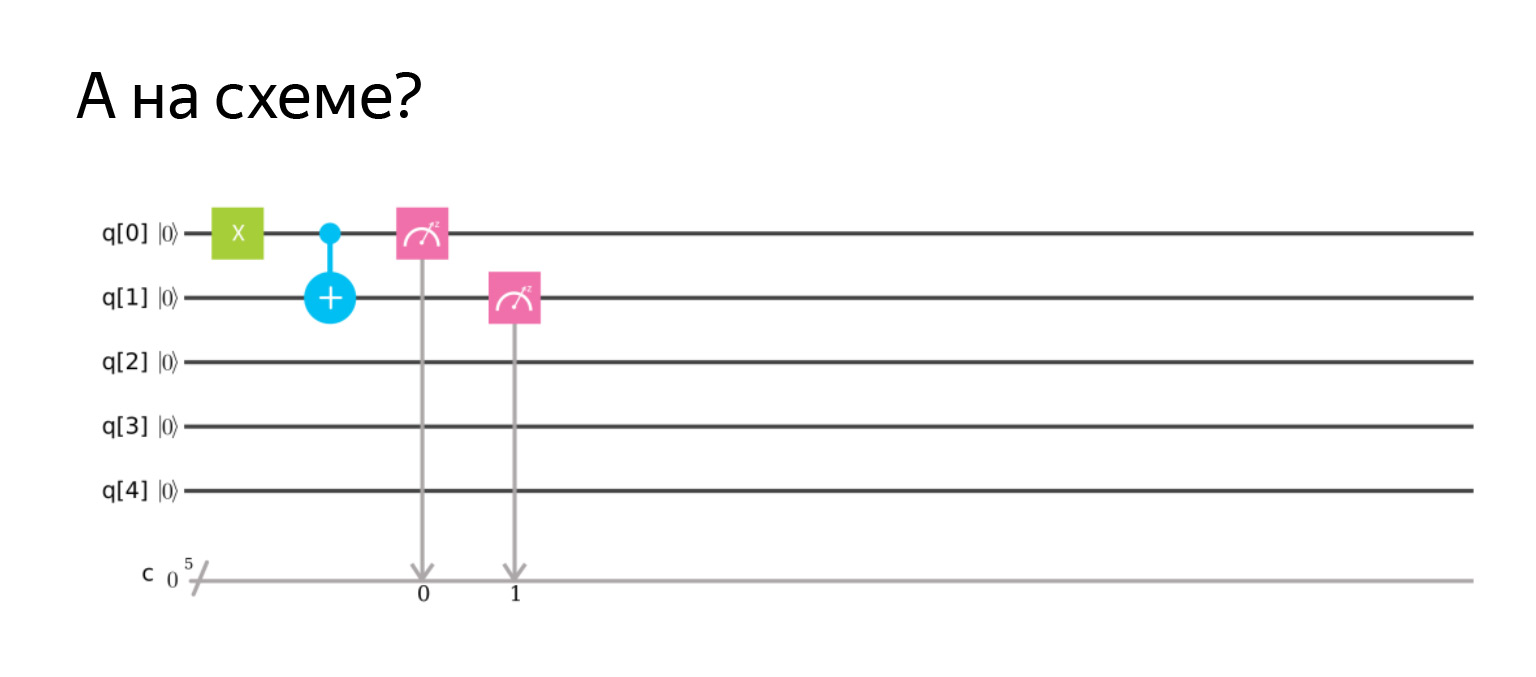
Es decir, la negación controlada es una ventaja en el qubit que queremos cambiar. Y el punto, que es el control. Aquí, si el qubit está en la unidad, entonces cambiaremos el segundo.

Aquí, primero invierto específicamente el primero para que sea uno, y luego mido ambos y obtengo el resultado | 11⟩. Todo es como lo esperábamos.
Pero ahora es el momento de usar todos nuestros conocimientos juntos.

Tomemos los tres o cuatro operadores que conocemos y pegámoslos en un esquema. Es decir, aplicamos el operador Hadamard al primer operador. Invierta el segundo, luego todos juntos, haga una negación controlada y mida.
No lo ejecutemos todavía, pero intente adivinar lo que sucederá.
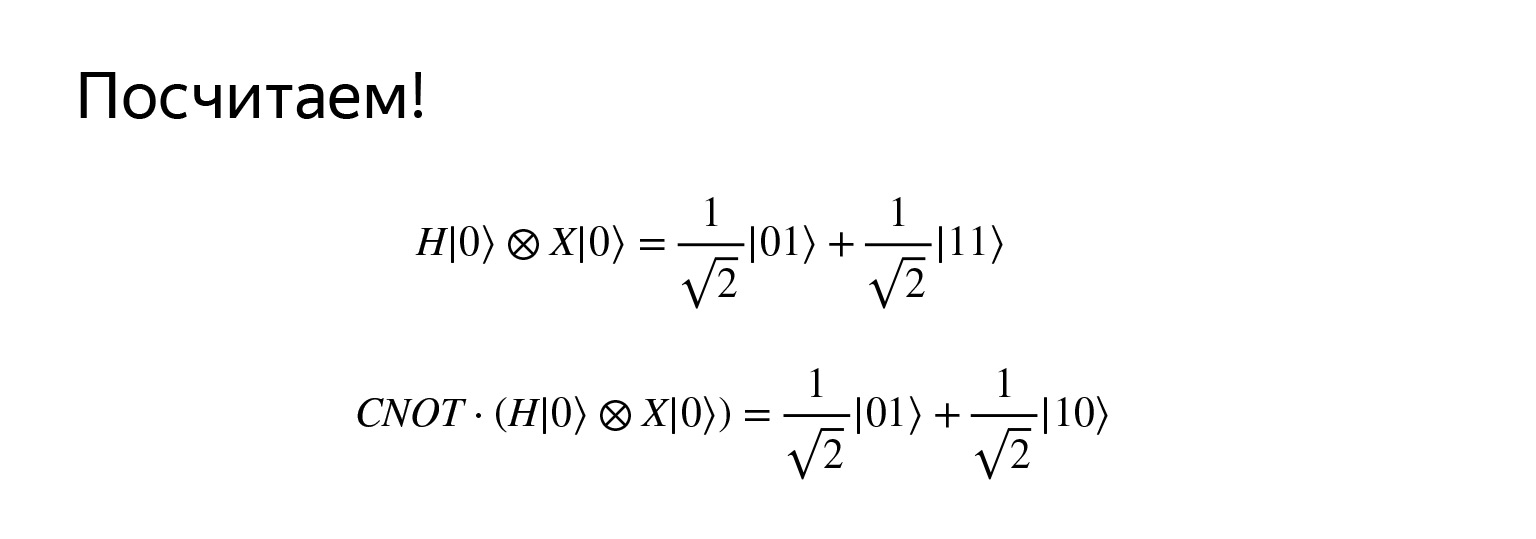
Si aplicamos el operador Hadamard al primer qubit y negamos el segundo, obtenemos tal superposición. No quiero perder tiempo comprobando ahora, se puede multiplicar fácilmente. Pero la posición es muy interesante. En primer lugar, es muy similar al uniforme y, en segundo lugar, ahora este estado se llama enredado, si también tomamos una negación controlada.

El estado es confuso. ¿Y por qué? Tratemos de hacer una medida. Mire, si mido el primer qubit y lo tengo en estado cero, entonces puedo decir que el segundo qubit está necesariamente en el estado uno.
Es decir, si realizo tal transformación con mis qubits, le doy un qubit a mi amigo, él volará a Nueva York, y mido el segundo qubit solo, sabré exactamente en qué estado está su qubit. Esto se llama el efecto del enredo cuántico o la conexión cuántica. Y este es el mecanismo principal por el cual funciona la computación cuántica. Cambiará, están muy rígidamente conectados y durante la medición solo podemos obtener | 00⟩ o | 11⟩.
En esta ocasión, hay una ilustración muy interesante a favor de un científico, austriaco, en mi opinión,

La distracción era que usaba medias diferentes todo el tiempo. Y sus colegas bromearon sobre él: si entra en la habitación con un pie y vemos que el calcetín es rosado, entonces definitivamente podemos decir que el segundo calcetín no es rosado. Así que va.
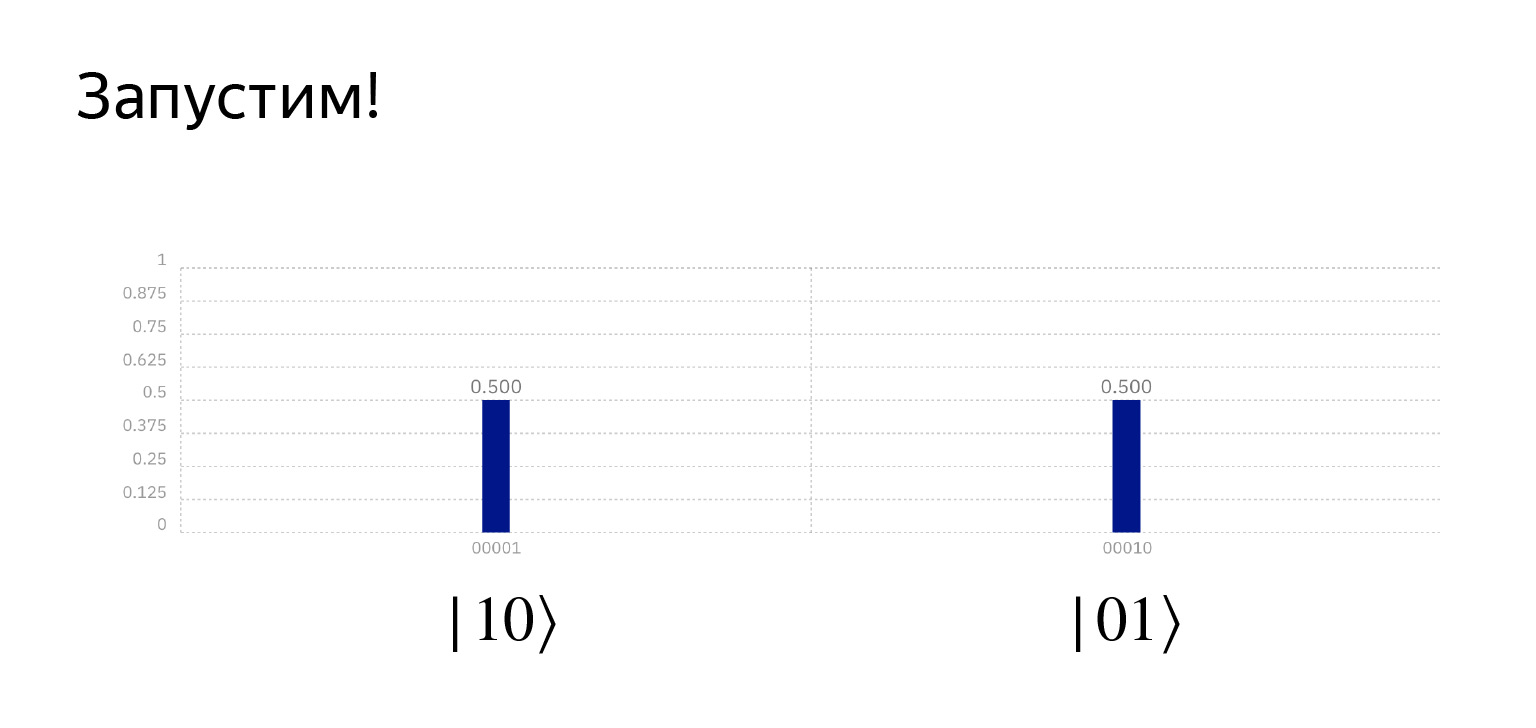
Si ejecutamos esto, obtenemos exactamente lo que queremos. Ya es bastante divertido aquí. La probabilidad es exactamente 0.5, pero esto es una coincidencia.
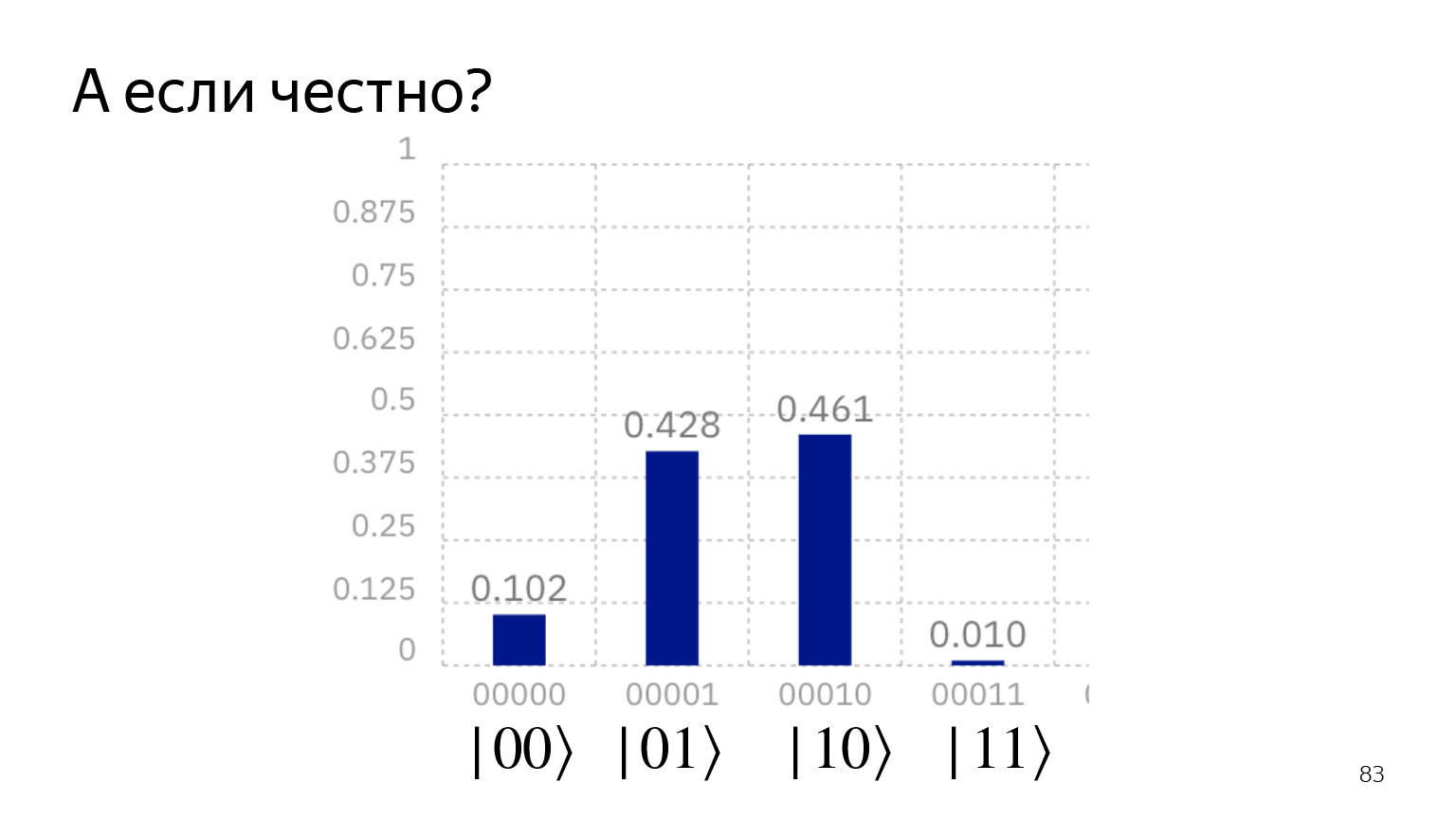
Si honestamente corremos en una computadora cuántica, obtenemos esta imagen. Parece que decimos: el estado | 00⟩ nunca se puede obtener y el estado | 11⟩ nunca se puede obtener. Pero aún funciona: el estado actual de la tecnología es tal que hay ruidos que no siempre se pueden suprimir fácilmente. Y están luchando con esto.
Pero si recuerdas la informática clásica, es lo mismo: códigos de corrección de errores y todo eso. Es solo que el qubit es demasiado pequeño por ahora para gastar bits adicionales en la corrección de errores.
Ahora, como prometí, algunos ejemplos de algoritmos. Pero estos serán solo ejemplos infundados sin análisis de algoritmos, de modo que se vea, piense y se interese.

El primer algoritmo está relacionado con Deutsch, del que hablamos al principio. Este es el algoritmo Deutsch-Jozy. Y él hace lo siguiente. Imagina que tenemos una función booleana en n variables. Y sabemos con certeza que es constante o equilibrado. Equilibrado significa que exactamente en la mitad de los argumentos es igual a cero, y en la otra mitad, a uno. Tratemos de verificar clásicamente si es constante o no.
Para hacer esto, debemos verificar al menos la mitad de todas las opciones posibles: opción 2 n - 1 +1. El algoritmo cuántico le permite hacer esto en n llamadas a la función misma, en n cálculos de la función misma. Este es un número exponencialmente menor de visitas.
El segundo ejemplo probablemente sea bien conocido por todos, por eso dicen que las computadoras cuánticas romperán toda la criptografía: podemos factorizar los números cuánticos muy rápidamente.

Las estimaciones de dificultad se dan aquí y hay un ejemplo fantástico. En 2011, el número 15 fue factorizado en una computadora real, tomó siete qubits.

Pero no todo es tan malo. En caso de que las computadoras cuánticas alcancen el nivel en el que puede romper el RSA, ya existe una criptografía post-cuántica. Se basa en el aprendizaje con errores. Esto es cuando se introduce un pequeño error en el problema, por lo que es muy difícil encontrar una respuesta. Por lo general, estos son algún tipo de ecuaciones o un sistema de ecuaciones. Aquí hay un ejemplo del algoritmo. Cualquiera que quiera puede leer con más detalle.
Lo más interesante: el algoritmo New Hope se basa en esta cosa , la nueva esperanza de toda la humanidad. En 2016, Chrome agregó soporte para este algoritmo. Hay un enlace al blog aquí. Esta no fue mi idea, todo lo es realmente. El futuro ya está aquí.
Hay algunos enlaces al final:
- , : Michael A.Nielsen and Isaac L. Chuang, «Quantum Computation and Quantum Information». , . .
- IBM Q: quantumexperience.ng.bluemix.net
- IBM Q User Guide: quantumexperience.ng.bluemix.net/proxy/tutorial/full-user-guide/introduction.html
- Qiskit: qiskit.org
- :
nplus1.ru/material/2017/06/07/quantumcomputers
nplus1.ru/news/2017/05/26/quantum-blockchain
Esto es más o menos todo. Solo quiero agregar que hace unos 50 años, cuando Deutsch comenzó a hacer ciencia de la información cuántica, las computadoras eran grandes. Fueron hechos por varias compañías. Eran del tamaño de un armario. Y ahora, aproximadamente las mismas compañías fabrican grandes computadoras cuánticas. Y, por supuesto, no sabemos qué pasará en 50 años.
Si intenta escribir su motor de búsqueda favorito, hoy puede encontrar vacantes para un programador cuántico. Claro, hay más investigación por ahí, pero no obstante. Gracias.