donde q es la carga de la partícula, r ij es la distancia entre partículas, C es algo constante dependiendo de la elección de las unidades de medida. En SI es - , en SGS - 1, en mi programa (donde la energía se expresa en voltios de electrones, la distancia en angstroms y la carga en cargas elementales) C es aproximadamente igual a 14.3996.
¿Y qué, dices? Simplemente agregue el término correspondiente al par potencial y ya está. Sin embargo, con mayor frecuencia en el modelado MD, se utilizan condiciones de contorno periódicas, es decir. El sistema simulado está rodeado por todos lados por un número infinito de sus copias virtuales. En este caso, cada imagen virtual de nuestro sistema interactuará con todas las partículas cargadas dentro del sistema de acuerdo con la ley de Coulomb. Y dado que la interacción de Coulomb disminuye muy débilmente con la distancia (como 1 / r), no es tan fácil descartarla, diciendo que no la calculamos a partir de tal o cual distancia. Una serie de la forma 1 / x diverge, es decir su cantidad, en principio, puede crecer indefinidamente. Y ahora, ¿no le salas un plato de sopa? ¿Te matará con electricidad?
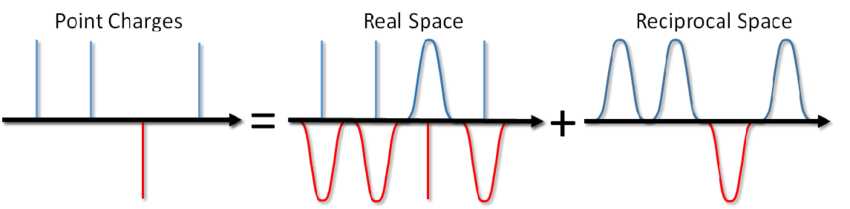
... no solo puedes salar la sopa, sino también calcular la energía de la interacción de Coulomb bajo condiciones de límite periódicas. Ewald propuso este método en 1921 para calcular la energía de un cristal iónico (también se puede ver en Wikipedia ). La esencia del método es seleccionar cargas puntuales y luego restar la función de detección. En este caso, una parte de la interacción electrostática se reduce a una de acción corta y simplemente se puede cortar de manera estándar. La parte restante de largo alcance se suma efectivamente en el espacio de Fourier. Omitiendo la conclusión, que puede verse en el artículo de Blinov o en el mismo libro de Frenkel y Smith , escribiré inmediatamente una solución llamada la suma de Ewald:
donde α es un parámetro que regula la relación de los cálculos en los espacios hacia adelante y hacia atrás, k son vectores en el espacio recíproco sobre el cual se realiza la suma, V es el volumen del sistema (en el espacio hacia adelante). La primera parte (E real ) es de corto alcance y se calcula en el mismo ciclo que los potenciales de los otros pares; consulte la función real_ewald en el artículo anterior. La última contribución ( Econst ) es una corrección para la auto-interacción y a menudo se llama la "parte constante" porque no depende de las coordenadas de las partículas. Su cálculo es trivial, por lo que nos centraremos solo en la segunda parte de la suma de Ewald (E rec), sumatoria en espacio recíproco. Naturalmente, en el momento de la derivación de Ewald, no había dinámica molecular; no pude encontrar quién utilizó este método por primera vez en MD. Hoy en día, cualquier libro sobre MD contiene su presentación como una especie de estándar de oro. Para reservar, Allen incluso proporcionó un código de ejemplo en Fortran. Afortunadamente, todavía tengo el código que una vez se escribió en C para la versión secuencial, solo queda para paralelizarlo (me permití omitir algunas declaraciones variables y otros detalles insignificantes):
void ewald_rec()
{
int mmin = 0;
int nmin = 1;
// iexp(x[i] * kx[l]),
double** elc;
double** els;
//... iexp(y[i] * ky[m])
double** emc;
double** ems;
//... iexp(z[i] * kz[n]),
double** enc;
double** ens;
// iexp(x*kx)*iexp(y*ky)
double* lmc;
double* lms;
// q[i] * iexp(x*kx)*iexp(y*ky)*iexp(z*kz)
double* ckc;
double* cks;
//
eng = 0.0;
for (i = 0; i < Nat; i++) //
{
// emc/s[i][0] enc/s[i][0]
// elc/s , .
elc[i][0] = 1.0;
els[i][0] = 0.0;
// iexp(kr)
sincos(twopi * xs[i] * ra, els[i][1], elc[i][1]);
sincos(twopi * ys[i] * rb, ems[i][1], emc[i][1]);
sincos(twopi * zs[i] * rc, ens[i][1], enc[i][1]);
}
// emc/s[i][l] = iexp(y[i]*ky[l]) ,
for (l = 2; l < ky; l++)
for (i = 0; i < Nat; i++)
{
emc[i][l] = emc[i][l - 1] * emc[i][1] - ems[i][l - 1] * ems[i][1];
ems[i][l] = ems[i][l - 1] * emc[i][1] + emc[i][l - 1] * ems[i][1];
}
// enc/s[i][l] = iexp(z[i]*kz[l]) ,
for (l = 2; l < kz; l++)
for (i = 0; i < Nat; i++)
{
enc[i][l] = enc[i][l - 1] * enc[i][1] - ens[i][l - 1] * ens[i][1];
ens[i][l] = ens[i][l - 1] * enc[i][1] + enc[i][l - 1] * ens[i][1];
}
// K-:
for (l = 0; l < kx; l++)
{
rkx = l * twopi * ra;
// exp(ikx[l]) ikx[0]
if (l == 1)
for (i = 0; i < Nat; i++)
{
elc[i][0] = elc[i][1];
els[i][0] = els[i][1];
}
else if (l > 1)
for (i = 0; i < Nat; i++)
{
// iexp(kx[0]) = iexp(kx[0]) * iexp(kx[1])
x = elc[i][0];
elc[i][0] = x * elc[i][1] - els[i][0] * els[i][1];
els[i][0] = els[i][0] * elc[i][1] + x * els[i][1];
}
for (m = mmin; m < ky; m++)
{
rky = m * twopi * rb;
// iexp(kx*x[i]) * iexp(ky*y[i])
if (m >= 0)
for (i = 0; i < Nat; i++)
{
lmc[i] = elc[i][0] * emc[i][m] - els[i][0] * ems[i][m];
lms[i] = els[i][0] * emc[i][m] + ems[i][m] * elc[i][0];
}
else // m :
for (i = 0; i < Nat; i++)
{
lmc[i] = elc[i][0] * emc[i][-m] + els[i][0] * ems[i][-m];
lms[i] = els[i][0] * emc[i][-m] - ems[i][-m] * elc[i][0];
}
for (n = nmin; n < kz; n++)
{
rkz = n * twopi * rc;
rk2 = rkx * rkx + rky * rky + rkz * rkz;
if (rk2 < rkcut2) //
{
// (q[i]*iexp(kr[k]*r[i])) -
sumC = 0; sumS = 0;
if (n >= 0)
for (i = 0; i < Nat; i++)
{
//
ch = charges[types[i]].charge;
ckc[i] = ch * (lmc[i] * enc[i][n] - lms[i] * ens[i][n]);
cks[i] = ch * (lms[i] * enc[i][n] + lmc[i] * ens[i][n]);
sumC += ckc[i];
sumS += cks[i];
}
else // :
for (i = 0; i < Nat; i++)
{
//
ch = charges[types[i]].charge;
ckc[i] = ch * (lmc[i] * enc[i][-n] + lms[i] * ens[i][-n]);
cks[i] = ch * (lms[i] * enc[i][-n] - lmc[i] * ens[i][-n]);
sumC += ckc[i];
sumS += cks[i];
}
//
akk = exp(rk2 * elec->mr4a2) / rk2;
eng += akk * (sumC * sumC + sumS * sumS);
for (i = 0; i < Nat; i++)
{
x = akk * (cks[i] * sumC - ckc[i] * sumS) * C * twopi * 2 * rvol;
fxs[i] += rkx * x;
fys[i] += rky * x;
fzs[i] += rkz * x;
}
}
} // end n-loop (over kz-vectors)
nmin = 1 - kz;
} // end m-loop (over ky-vectors)
mmin = 1 - ky;
} // end l-loop (over kx-vectors)
engElec2 = eng * * twopi * rvol;
}
Un par de explicaciones para el código: la función calcula el exponente complejo (en los comentarios al código se denota iexp para eliminar la unidad imaginaria de los corchetes) del producto vectorial del vector k y el vector radio de la partícula para todos los vectores k y para todas las partículas. Este exponente se multiplica por la carga de partículas. Luego, se calcula la suma de tales productos para todas las partículas (la suma interna en la fórmula para E rec ), en Frenkel se llama densidad de carga, y en Blinov se llama factor estructural. Y luego, sobre la base de estos factores estructurales, se calcula la energía y las fuerzas que actúan sobre las partículas. Los componentes de k-vectores (2π * l / a, 2π * m / b, 2π * n / c) se caracterizan por tres números enteros l , m y n, que se ejecutan en ciclos hasta los límites especificados por el usuario. Los parámetros a, byc son las dimensiones del sistema simulado en las dimensiones x, y y z, respectivamente (la conclusión es correcta para un sistema con una geometría paralelepípeda rectangular). En el código, 1 / a , 1 / b, y 1 / c corresponden a las variables ra , rb, y rc . Las matrices para cada valor se presentan en dos copias: para las partes real e imaginaria. Cada siguiente k-vector en una dimensión se obtiene iterativamente del anterior mediante la multiplicación compleja del anterior por uno, a fin de no contar el seno con coseno cada vez. El EMC / s y enc / s arrays se rellenan para todos my n , respectivamente, y la matriz de ELC / s lugares el valor para cada l > 1 en el índice cero de l con el fin de ahorrar memoria.
A los efectos de la paralelización, es ventajoso "invertir" el orden de los ciclos para que el ciclo externo se ejecute sobre las partículas. Y aquí vemos un problema: esta función se puede paralelizar solo antes de calcular la suma de todas las partículas (densidad de carga). Los cálculos adicionales se basan en esta cantidad, y se calculará solo cuando todos los hilos terminen su trabajo, por lo que debe dividir esta función en dos. El primero calcula la densidad de carga, y el segundo calcula la energía y las fuerzas. Tenga en cuenta que la segunda función requerirá nuevamente la cantidad q iiexp (kr) para cada partícula y para cada vector k, calculado en el paso anterior. Y aquí hay dos enfoques: volver a calcularlo o recordarlo.
La primera opción lleva más tiempo, la segunda: más memoria (número de partículas * número de k-vectores * sizeof (float2)). Me decidí por la segunda opción:
__global__ void recip_ewald(int atPerBlock, int atPerThread, cudaMD* md)
// calculate reciprocal part of Ewald summ
// the first part : summ (qiexp(kr)) evaluation
{
int i; // for atom loop
int ik; // index of k-vector
int l, m, n;
int mmin = 0;
int nmin = 1;
float tmp, ch;
float rkx, rky, rkz, rk2; // component of rk-vectors
int nkx = md->nk.x;
int nky = md->nk.y;
int nkz = md->nk.z;
// arrays for keeping iexp(k*r) Re and Im part
float2 el[2];
float2 em[NKVEC_MX];
float2 en[NKVEC_MX];
float2 sums[NTOTKVEC]; // summ (q iexp (k*r)) for each k
extern __shared__ float2 sh_sums[]; // the same in shared memory
float2 lm; // temp var for keeping el*em
float2 ck; // temp var for keeping q * el * em * en (q iexp (kr))
// invert length of box cell
float ra = md->revLeng.x;
float rb = md->revLeng.y;
float rc = md->revLeng.z;
if (threadIdx.x == 0)
for (i = 0; i < md->nKvec; i++)
sh_sums[i] = make_float2(0.0f, 0.0f);
__syncthreads();
for (i = 0; i < md->nKvec; i++)
sums[i] = make_float2(0.0f, 0.0f);
int id0 = blockIdx.x * atPerBlock + threadIdx.x * atPerThread;
int N = min(id0 + atPerThread, md->nAt);
ik = 0;
for (i = id0; i < N; i++)
{
// save charge
ch = md->specs[md->types[i]].charge;
el[0] = make_float2(1.0f, 0.0f); // .x - real part (or cos) .y - imagine part (or sin)
em[0] = make_float2(1.0f, 0.0f);
en[0] = make_float2(1.0f, 0.0f);
// iexp (ikr)
sincos(d_2pi * md->xyz[i].x * ra, &(el[1].y), &(el[1].x));
sincos(d_2pi * md->xyz[i].y * rb, &(em[1].y), &(em[1].x));
sincos(d_2pi * md->xyz[i].z * rc, &(en[1].y), &(en[1].x));
// fil exp(iky) array by complex multiplication
for (l = 2; l < nky; l++)
{
em[l].x = em[l - 1].x * em[1].x - em[l - 1].y * em[1].y;
em[l].y = em[l - 1].y * em[1].x + em[l - 1].x * em[1].y;
}
// fil exp(ikz) array by complex multiplication
for (l = 2; l < nkz; l++)
{
en[l].x = en[l - 1].x * en[1].x - en[l - 1].y * en[1].y;
en[l].y = en[l - 1].y * en[1].x + en[l - 1].x * en[1].y;
}
// MAIN LOOP OVER K-VECTORS:
for (l = 0; l < nkx; l++)
{
rkx = l * d_2pi * ra;
// move exp(ikx[l]) to ikx[0] for memory saving (ikx[i>1] are not used)
if (l == 1)
el[0] = el[1];
else if (l > 1)
{
// exp(ikx[0]) = exp(ikx[0]) * exp(ikx[1])
tmp = el[0].x;
el[0].x = tmp * el[1].x - el[0].y * el[1].y;
el[0].y = el[0].y * el[1].x + tmp * el[1].y;
}
//ky - loop:
for (m = mmin; m < nky; m++)
{
rky = m * d_2pi * rb;
//set temporary variable lm = e^ikx * e^iky
if (m >= 0)
{
lm.x = el[0].x * em[m].x - el[0].y * em[m].y;
lm.y = el[0].y * em[m].x + em[m].y * el[0].x;
}
else // for negative ky give complex adjustment to positive ky:
{
lm.x = el[0].x * em[-m].x + el[0].y * em[-m].y;
lm.y = el[0].y * em[-m].x - em[-m].x * el[0].x;
}
//kz - loop:
for (n = nmin; n < nkz; n++)
{
rkz = n * d_2pi * rc;
rk2 = rkx * rkx + rky * rky + rkz * rkz;
if (rk2 < md->rKcut2) // cutoff
{
// calculate summ[q iexp(kr)] (local part)
if (n >= 0)
{
ck.x = ch * (lm.x * en[n].x - lm.y * en[n].y);
ck.y = ch * (lm.y * en[n].x + lm.x * en[n].y);
}
else // for negative kz give complex adjustment to positive kz:
{
ck.x = ch * (lm.x * en[-n].x + lm.y * en[-n].y);
ck.y = ch * (lm.y * en[-n].x - lm.x * en[-n].y);
}
sums[ik].x += ck.x;
sums[ik].y += ck.y;
// save qiexp(kr) for each k for each atom:
md->qiexp[i][ik] = ck;
ik++;
}
} // end n-loop (over kz-vectors)
nmin = 1 - nkz;
} // end m-loop (over ky-vectors)
mmin = 1 - nky;
} // end l-loop (over kx-vectors)
} // end loop by atoms
// save sum into shared memory
for (i = 0; i < md->nKvec; i++)
{
atomicAdd(&(sh_sums[i].x), sums[i].x);
atomicAdd(&(sh_sums[i].y), sums[i].y);
}
__syncthreads();
//...and to global
int step = ceil((double)md->nKvec / (double)blockDim.x);
id0 = threadIdx.x * step;
N = min(id0 + step, md->nKvec);
for (i = id0; i < N; i++)
{
atomicAdd(&(md->qDens[i].x), sh_sums[i].x);
atomicAdd(&(md->qDens[i].y), sh_sums[i].y);
}
}
// end 'ewald_rec' function
__global__ void ewald_force(int atPerBlock, int atPerThread, cudaMD* md)
// calculate reciprocal part of Ewald summ
// the second part : enegy and forces
{
int i; // for atom loop
int ik; // index of k-vector
float tmp;
// accumulator for force components
float3 force;
// constant factors for energy and force
float eScale = md->ewEscale;
float fScale = md->ewFscale;
int id0 = blockIdx.x * atPerBlock + threadIdx.x * atPerThread;
int N = min(id0 + atPerThread, md->nAt);
for (i = id0; i < N; i++)
{
force = make_float3(0.0f, 0.0f, 0.0f);
// summ by k-vectors
for (ik = 0; ik < md->nKvec; ik++)
{
tmp = fScale * md->exprk2[ik] * (md->qiexp[i][ik].y * md->qDens[ik].x - md->qiexp[i][ik].x * md->qDens[ik].y);
force.x += tmp * md->rk[ik].x;
force.y += tmp * md->rk[ik].y;
force.z += tmp * md->rk[ik].z;
}
md->frs[i].x += force.x;
md->frs[i].y += force.y;
md->frs[i].z += force.z;
} // end loop by atoms
// one block calculate energy
if (blockIdx.x == 0)
if (threadIdx.x == 0)
{
for (ik = 0; ik < md->nKvec; ik++)
md->engCoul2 += eScale * md->exprk2[ik] * (md->qDens[ik].x * md->qDens[ik].x + md->qDens[ik].y * md->qDens[ik].y);
}
}
// end 'ewald_force' function
Espero que me perdones por dejar comentarios en inglés, el código es prácticamente el mismo que la versión en serie. El código incluso se hizo más legible debido al hecho de que las matrices perdieron una dimensión: elc / s [i] [l] , emc / s [i] [m] y enc / s [i] [n] se convirtieron en unidimensional el , em y en , arrays LMC / s y ckc / s - en las variables LM y ck (dimensión por las partículas ha desaparecido, puesto que ya no es la necesidad de almacenar para cada partícula, el resultado intermedio se acumula en la memoria compartida). Desafortunadamente, surgió un problema de inmediato: las matrices em y entuvo que establecerse estática para no usar memoria global y no asignar memoria dinámicamente cada vez. El número de elementos en ellos está determinado por la directiva NKVEC_MX (el número máximo de k-vectores en una dimensión) en la etapa de compilación, y solo los primeros elementos nky / z se usan en tiempo de ejecución. Además, apareció un índice de extremo a extremo en todos los k-vectores y una directiva similar, limitando el número total de estos vectores NTOTKVEC . El problema surgirá si el usuario necesita más k-vectores que los especificados por las directivas. Para calcular la energía, se proporciona un bloque con un índice cero, ya que no importa qué bloque realizará este cálculo y en qué orden. Tenga en cuenta que el valor calculado en la variable akkel código de serie depende solo del tamaño del sistema simulado y puede calcularse en la etapa de inicialización, en mi implementación se almacena en la matriz md-> exprk2 [] para cada vector k. Del mismo modo, los componentes de los k-vectores se toman de la matriz md-> rk [] . Aquí podría ser necesario usar funciones FFT listas para usar, ya que el método se basa en él, pero aún no descubrí cómo hacerlo.
Bueno, ahora intentemos contar algo, pero el mismo cloruro de sodio. Tomemos 2 mil iones de sodio y la misma cantidad de cloro. Establezcamos las cargas como enteros y tomemos potenciales de pares, por ejemplo, de este trabajo.... Establezcamos la configuración inicial al azar y mezclemos ligeramente, Figura 2a. Elegimos el volumen del sistema para que corresponda a la densidad de cloruro de sodio a temperatura ambiente (2.165 g / cm 3 ). Comencemos todo esto por un corto tiempo (10'000 pasos de 5 femtosegundos) con una ingenua consideración de la electrostática de acuerdo con la ley de Coulomb y usando la suma de Ewald. Las configuraciones resultantes se muestran en las Figuras 2b y 2c, respectivamente. Parece que en el caso de Ewald, el sistema es un poco más aerodinámico que sin él. También es importante que las fluctuaciones totales de energía hayan disminuido significativamente con el uso de la sumatoria.

Figura 2. Configuración inicial del sistema NaCl (a) y después de 10'000 pasos de integración: método ingenuo (b) y con el esquema Ewald (c).
En lugar de una conclusión
Tenga en cuenta que la estructura obtenida en la figura no corresponde a la red cristalina de NaCl, sino a la red ZnS, pero esto ya es una queja sobre los potenciales de los pares. Tener en cuenta la electrostática es muy importante para el modelado de dinámica molecular. Se cree que es la interacción electrostática la responsable de la formación de las redes cristalinas, ya que actúa a grandes distancias. Es cierto que desde esta posición es difícil explicar cómo se cristalizan sustancias como el argón durante el enfriamiento.
Además del método de Ewald mencionado, también hay otros métodos de contabilización de la electrostática, consulte, por ejemplo, esta revisión .