FAISS: encuentre rápidamente caras y clones en datos multimillonarios

Una vez, en la víspera de la conferencia de clientes, que se realiza anualmente por el grupo DAN, estábamos pensando en qué cosas interesantes podemos pensar para que nuestros socios y clientes tengan impresiones agradables y recuerdos del evento. Decidimos hacer un archivo de miles de fotos de esta conferencia y varias pasadas (y había 18 en total para ese momento): una persona nos envía su foto, y en un par de segundos le enviamos una selección de fotos con él durante varios años desde nuestros archivos.



No inventamos una bicicleta, llevamos la conocida biblioteca dlib a todos y recibimos incrustaciones (representaciones vectoriales) de cada persona. 



Agregamos un bot de Telegram por conveniencia, y todo fue genial. Desde el punto de vista de los algoritmos de reconocimiento facial, todo funcionó de maravilla, pero la conferencia terminó y no quería separarme de las tecnologías probadas. Queríamos pasar de varios miles de personas a cientos de millones, pero no teníamos una tarea comercial específica. Después de un tiempo, nuestros colegas tenían una tarea que requería trabajar con cantidades tan grandes de datos.



La pregunta era escribir un sistema inteligente de monitoreo de bots dentro de la red de Instagram. Aquí nuestro pensamiento dio lugar a un enfoque simple y complejo:



forma simple: consideramos todas las cuentas que tienen muchas más suscripciones que suscriptores, sin avatar, el nombre completo no está completo, etc. Como resultado, obtenemos una multitud incomprensible de cuentas medio muertas.



El camino difícil: dado que los robots modernos se han vuelto mucho más inteligentes, y ahora publican publicaciones, duermen e incluso escriben contenido, surge la pregunta: ¿cómo atraparlos? En primer lugar, vigile de cerca a sus amigos, ya que a menudo también son bots, y rastree fotos duplicadas. En segundo lugar, rara vez un bot sabe cómo generar sus propias imágenes (aunque esto es posible), lo que significa que las fotos duplicadas de personas en diferentes cuentas en Instagram son un buen disparador para encontrar una red de bots.

¿Que sigue?

Si un camino simple es bastante predecible y rápidamente da algunos resultados, entonces un camino difícil es difícil precisamente porque para implementarlo tendremos que vectorizar e indexar volúmenes increíblemente grandes de fotografías para comparaciones posteriores de similitudes: millones e incluso miles de millones. ¿Cómo ponerlo en práctica? Después de todo, surgen preguntas técnicas:

1. Velocidad de búsqueda y precisión
2. Espacio en disco ocupado por los datos
3. El tamaño de la RAM utilizada. 

Si solo hubiera unas pocas fotos, al menos no más de diez mil, podríamos limitarnos a soluciones simples con agrupación de vectores, pero para trabajar con grandes volúmenes de vectores y encontrar los vecinos más cercanos a un determinado vector, se requieren algoritmos complejos y optimizados.



Existen tecnologías conocidas y probadas, como Annoy, FAISS, HNSW. Algoritmo de búsqueda rápida de vecinos HNSW disponible en las bibliotecas nmslib y hnswlib, muestra resultados de vanguardia en la CPU, que se pueden ver desde los mismos puntos de referencia. Pero lo cortamos de inmediato, ya que no estamos contentos con la cantidad de memoria utilizada cuando trabajamos con grandes cantidades de datos. Comenzamos a elegir entre Annoy y FAISS y al final elegimos FAISS por conveniencia, menor uso de memoria, uso potencial en la GPU y puntos de referencia para el rendimiento (puede ver, por ejemplo, aquí ). Por cierto, en FAISS, el algoritmo HNSW se implementa como una opción.

¿Qué es FAISS?

Facebook AI Research Similarity Search es un desarrollo del equipo de Facebook AI Research para encontrar rápidamente vecinos cercanos y agruparlos en el espacio vectorial. La alta velocidad de búsqueda permite trabajar con datos muy grandes, hasta varios miles de millones de vectores.



La principal ventaja de FAISS es sus resultados de vanguardia en la GPU, mientras que su implementación en la CPU es ligeramente inferior a hnsw (nmslib). Queríamos poder buscar tanto en la CPU como en la GPU. Además, FAISS está optimizado en términos de uso de memoria y búsqueda en grandes lotes.



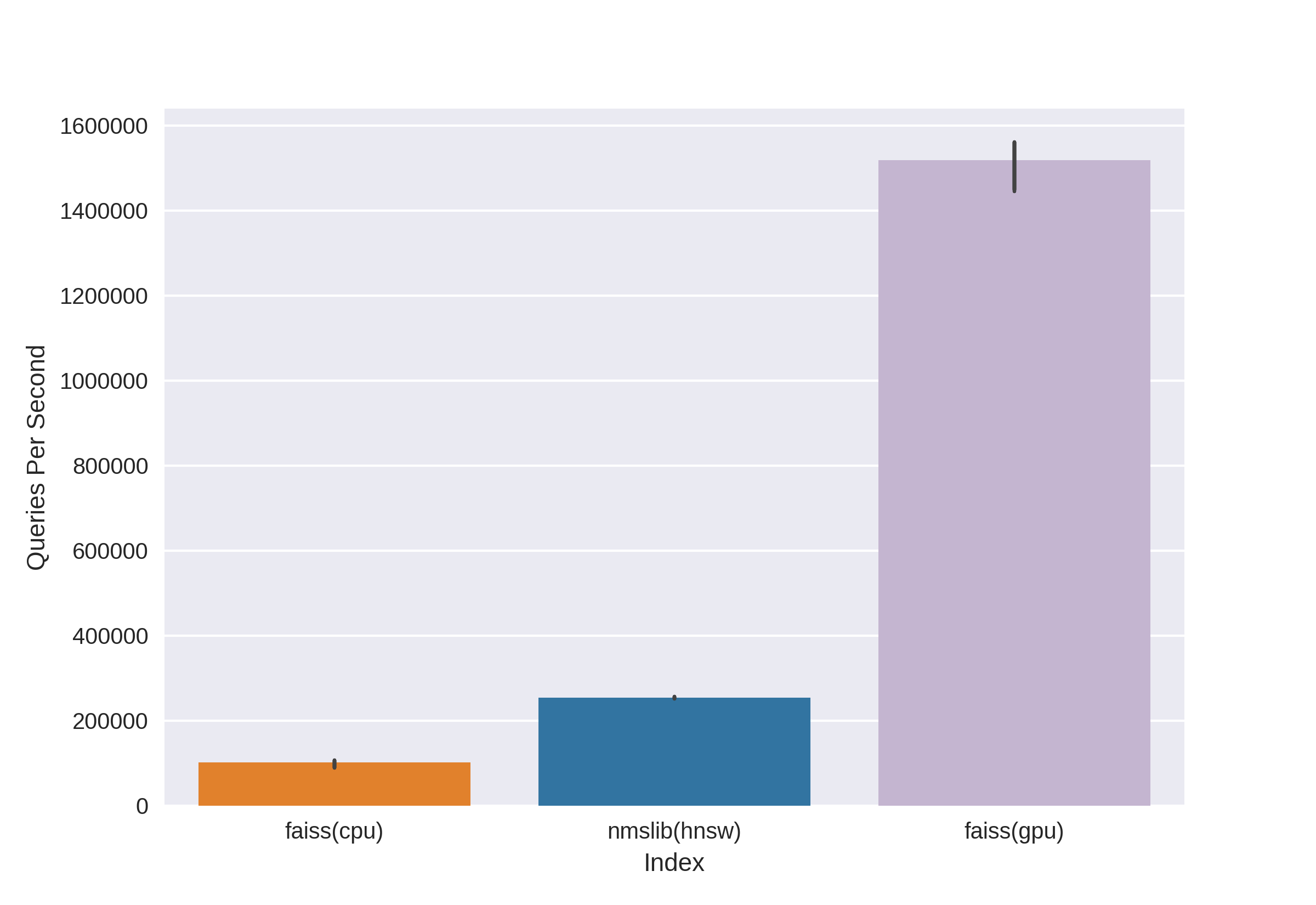
Source



FAISS le permite encontrar rápidamente los k vectores más cercanos para un vector dado x. Pero, ¿cómo funciona esta búsqueda bajo el capó?

Índices

El concepto principal en FAISS es el índice y, de hecho, es solo una colección de parámetros y vectores. Los conjuntos de parámetros son completamente diferentes y dependen de las necesidades del usuario. Los vectores pueden permanecer sin cambios, pero pueden reconstruirse. Algunos índices están disponibles para trabajar inmediatamente después de agregarles vectores, y algunos requieren capacitación previa. Los nombres de los vectores se almacenan en el índice: ya sea en la numeración de 0 a n, o como un número que se ajusta al tipo Int64.



El primer índice, y el más simple que utilizamos en la conferencia, es Flat . Solo almacena todos los vectores en sí mismo, y la búsqueda de un vector dado se realiza mediante una búsqueda exhaustiva, por lo que no hay necesidad de entrenarlo (pero más información sobre el entrenamiento a continuación). En una pequeña cantidad de datos, un índice tan simple puede cubrir sus necesidades de búsqueda.



Ejemplo:

import numpy as np
dim = 512  #     512
nb = 10000  #    
nq = 5 #      
np.random.seed(228)
vectors = np.random.random((nb, dim)).astype('float32')
query = np.random.random((nq, dim)).astype('float32')

Cree un índice plano y agregue vectores sin capacitación:

import faiss
index = faiss.IndexFlatL2(dim)
print(index.ntotal)  #   
index.add(vectors)
print(index.ntotal)  #    10 000 

Ahora busquemos los 7 vecinos más cercanos para los primeros cinco vectores de vectores:

topn = 7
D, I = index.search(vectors[:5], topn)  #  : Distances, Indices
print(I)
print(D)

Vemos que los vecinos más cercanos con una distancia de 0 son los propios vectores, el resto se alinean al aumentar la distancia. Busquemos nuestros vectores desde la consulta:

D, I = index.search(query, topn) 
print(I)
print(D)

Ahora las distancias en la primera columna de los resultados no son cero, ya que los vectores de consulta no están en el índice.



El índice puede guardarse en el disco y luego cargarse desde el disco:

faiss.write_index(index, "flat.index")
index = faiss.read_index("flat.index")

¡Parece que todo es elemental! Algunas líneas de código, y ya tenemos una estructura para buscar vectores de alta dimensión. Pero dicho índice con solo diez millones de vectores de dimensión 512 pesará alrededor de 20 GB y ocupará la misma cantidad de RAM cuando lo use.



En el proyecto para la conferencia, utilizamos un enfoque tan básico con un índice plano, todo fue genial debido a la cantidad relativamente pequeña de datos, ¡pero ahora estamos hablando de decenas y cientos de millones de vectores de alta dimensión!

Acelere su búsqueda con listas invertidas

Fuente



La característica principal y más genial de FAISS es el índice de FIV o elíndice de archivo invertido . La idea de los archivos invertidos es lacónica, y está bellamente explicada con los dedos :



imaginemos un ejército gigantesco que consta de los guerreros más multicolores, que suman, digamos, 1,000,000 de personas. Dirigir todo un ejército a la vez será imposible. Como es habitual en los asuntos militares, necesitamos dividir nuestro ejército en subunidades. Dividámonos en$$partes aproximadamente iguales por comandantes en el papel de representante de cada división. E intentaremos enviar los más similares en carácter, origen, datos físicos, etc. guerreros en una unidad, y elegiremos al comandante para que represente a su unidad con la mayor precisión posible: es alguien "promedio". Como resultado, nuestra tarea se redujo de comandar un millón de soldados a comandar 1000 unidades a través de sus comandantes, y tenemos una excelente idea de la composición de nuestro ejército, ya que sabemos qué son los comandantes. Esta es la idea detrás del índice de FIV: agrupemos un gran conjunto de vectores pieza por pieza usando el algoritmok-means$\sqrt{1 000 000} = 1000$



, establecer cada parte de acuerdo con el centroide, es un vector que es el centro seleccionado para un grupo dado. La búsqueda se llevará a cabo a través de la distancia mínima al centroide, y solo entonces buscaremos las distancias mínimas entre los vectores en el grupo que corresponde al centroide dado. Tomando k igual$$ , donde$\sqrt{n}$$$ es el número de vectores en el índice, obtendremos una búsqueda óptima en dos niveles, el primero entre$n$$$ centroide, luego entre$\sqrt{n}$$$ vectores en cada grupo. La búsqueda es mucho más rápida que la búsqueda de fuerza bruta, que resuelve uno de nuestros problemas cuando trabajamos con muchos millones de vectores. El espacio vectorial se divide por el método k-medias en k grupos. A cada grupo se le asigna un centroide Código de ejemplo:$\sqrt{n}$

dim = 512
k = 1000  #  “”
quantiser = faiss.IndexFlatL2(dim) 
index = faiss.IndexIVFFlat(quantiser, dim, k)
vectors = np.random.random((1000000, dim)).astype('float32')  # 1 000 000 “”

Y puede escribirlo de manera mucho más elegante, utilizando la práctica herramienta FAISS para crear el índice:

index = faiss.index_factory(dim, “IVF1000,Flat”)
 :
print(index.is_trained)   # False.
index.train(vectors)  # Train    
 
#  ,      ,      :
print(index.is_trained)  # True
print(index.ntotal)   # 0
index.add(vectors)
print(index.ntotal)   # 1000000

Después de considerar este tipo de índice después de Flat, resolvimos uno de nuestros problemas potenciales: la velocidad de búsqueda, que se vuelve varias veces más lenta en comparación con una búsqueda completa.

D, I = index.search(query, topn) 
print(I)
print(D)

Pero hay un "pero": la precisión de la búsqueda, así como la velocidad, dependerán de la cantidad de clústeres visitados, que se pueden configurar con el parámetro nprobe:

print(index.nprobe)  # 1 –           
index.nprobe = 16  #   -16    top-n  
D, I = index.search(query, topn) 
print(I)
print(D)

Como puede ver, después de aumentar nprobe, tenemos resultados completamente diferentes, la parte superior de las distancias más pequeñas en D mejoró.



Puede tomar nprobe igual al número de centroides en el índice, entonces esto será equivalente a buscar por búsqueda exhaustiva, la precisión será mayor, pero la velocidad de búsqueda disminuirá notablemente.

Búsqueda en el disco: listas invertidas en disco

¡Genial, resolvimos el primer problema, ahora tenemos una velocidad de búsqueda aceptable en decenas de millones de vectores! Pero todo esto es inútil siempre que nuestro enorme índice no se ajuste a la RAM.



Específicamente para nuestra tarea, la principal ventaja de FAISS es la capacidad de almacenar Listas Invertidas del índice de FIV en el disco, cargando solo metadatos en la RAM.



¿Cómo creamos dicho índice? Entrenamos indexIVF con los parámetros necesarios sobre la cantidad máxima posible de datos que cabe en la memoria, luego agregamos vectores (aquellos que han sido entrenados y no solo) al índice entrenado en partes y escribimos el índice para cada una de las partes en el disco.

index = faiss.index_factory(512, “,IVF65536, Flat”, faiss.METRIC_L2)

Entrenamos el índice en la GPU de esta manera:

res = faiss.StandardGpuResources()
index_ivf = faiss.extract_index_ivf(index)
index_flat = faiss.IndexFlatL2(512)
clustering_index = faiss.index_cpu_to_gpu(res, 0, index_flat)  #  0 –  GPU
index_ivf.clustering_index = clustering_index

faiss.index_cpu_to_gpu (res, 0, index_flat) se puede reemplazar con faiss.index_cpu_to_all_gpus (index_flat) para usar todas las GPU juntas.



Es altamente deseable que la muestra de entrenamiento sea lo más representativa posible y tenga una distribución uniforme, por lo que precomponemos el conjunto de datos de entrenamiento del número requerido de vectores, seleccionándolos aleatoriamente de todo el conjunto de datos.

train_vectors = ...  #     
index.train(train_vectors)

#    ,   :
faiss.write_index(index, "trained_block.index") 

#       
#      :
for bno in range(first_block, last_block+ 1):
    block_vectors = vectors_parts[bno]
    block_vectors_ids = vectors_parts_ids[bno]  # id ,  
    index = faiss.read_index("trained_block.index")
    index.add_with_ids(block_vectors, block_vectors_ids)
    faiss.write_index(index, "block_{}.index".format(bno))

Después de eso, combinamos todas las Listas Invertidas juntas. Esto es posible, ya que cada uno de los bloques es esencialmente el mismo índice entrenado, solo que con diferentes vectores dentro.

ivfs = []
for bno in range(first_block, last_block+ 1):
    index = faiss.read_index("block_{}.index".format(bno), faiss.IO_FLAG_MMAP)
    ivfs.append(index.invlists)
    #  index   inv_lists 
    #        :
    index.own_invlists = False

#   :
index = faiss.read_index("trained_block.index")

#   invlists
#  invlists       merged_index.ivfdata
invlists = faiss.OnDiskInvertedLists(index.nlist, index.code_size, "merged_index.ivfdata")
ivf_vector = faiss.InvertedListsPtrVector() 

for ivf in ivfs: 
    ivf_vector.push_back(ivf)

ntotal = invlists.merge_from(ivf_vector.data(), ivf_vector.size())
index.ntotal = ntotal  #     
index.replace_invlists(invlists)  
faiss.write_index(index, data_path + "populated.index")  #    

En pocas palabras: ahora nuestro índice es populated.index y archivos merged_blocks.ivfdata .



En populated.index registró la ruta completa original al archivo con las Listas Invertidas, por lo que si la ruta del archivo ivfdata por alguna razón, el cambio en la lectura del índice necesitará usar el indicador faiss.IO_FLAG_ONDISK_SAME_DIR , que le permite buscar el archivo ivfdata en el mismo directorio que el populated.index:

index = faiss.read_index('populated.index', faiss.IO_FLAG_ONDISK_SAME_DIR)

El ejemplo de demostración del proyecto Github FAISS se tomó como base .



Puede encontrar una mini guía para elegir un índice en el Wiki de FAISS . Por ejemplo, pudimos colocar un conjunto de datos de entrenamiento de 12 millones de vectores en RAM, por lo que elegimos el índice IVFFlat en 262144 centroides y luego lo escalamos a cientos de millones. La guía también propone usar el índice IVF262144_HNSW32, en el que el vector que pertenece al clúster está determinado por el algoritmo HNSW con 32 vecinos más cercanos (en otras palabras, se usa el cuantificador IndexHNSWFlat), pero, como nos pareció durante otras pruebas, la búsqueda de dicho índice es menos precisa. Además, debe tenerse en cuenta que dicho cuantificador excluye la posibilidad de usar en la GPU.

Uso de disco significativamente reducido con la cuantificación del producto

Gracias al método de búsqueda de disco, fue posible eliminar la carga de la RAM, pero un índice con un millón de vectores todavía tomó alrededor de 2 GB de espacio en disco, y estamos hablando de la posibilidad de trabajar con miles de millones de vectores, ¡lo que requeriría más de dos TB! Por supuesto, el volumen no es tan grande si establece un objetivo y asigna espacio de disco adicional, pero nos molestó un poco.



Y aquí la codificación vectorial viene al rescate, a saber, la cuantificación escalar (SQ) y la cuantificación del producto (PQ). SQ: codifica cada componente del vector en n bits (generalmente 8, 6 o 4 bits). Consideraremos la opción PQ, porque la idea de codificar un solo componente de tipo float32 con ocho bits parece demasiado deprimente en términos de precisión. Aunque en algunos casos la compresión de SQfp16 a float16 tendrá una precisión casi sin pérdidas.



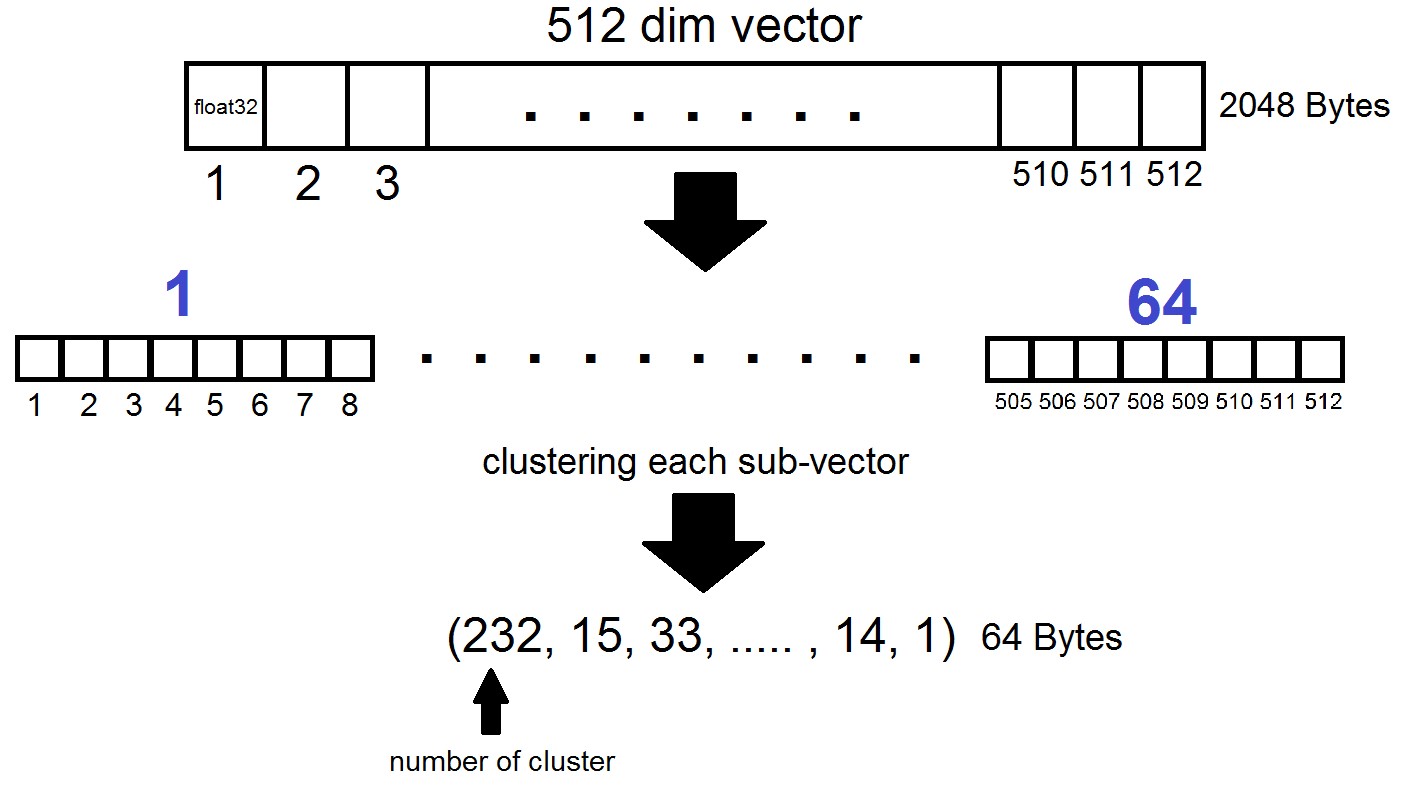
La esencia de la cuantificación del producto es la siguiente: los vectores de dimensión 512 se dividen en n partes, cada una de las cuales se agrupa en 256 grupos posibles (1 byte), es decir, representamos un vector con n bytes, donde n es generalmente como máximo 64 en una implementación FAISS. ¡Pero tal cuantización se aplica no a los vectores del conjunto de datos en sí, sino a las diferencias de estos vectores y los centroides correspondientes obtenidos durante la generación de Listas Invertidas! Resulta que las Listas Invertidas serán conjuntos codificados de distancias entre vectores y sus centroides.

index = faiss.index_factory(dim, "IVF262144,PQ64", faiss.METRIC_L2)

Resulta que ahora no es necesario que almacenemos todos los vectores: es suficiente asignar n bytes por vector y 2048 bytes por cada vector centroide. En nuestro caso, tomamos$$ , es decir$n = 64$$$: la longitud de un subvector, que se define en uno de los 256 grupos. Al buscar por el vector x, los centroides más cercanos se determinarán primero con el cuantificador plano habitual, y luego x también se divide en sub-vectores, cada uno de los cuales está codificado por el número de uno de los 256 centroides correspondientes. Y la distancia al vector se define como la suma de 64 distancias entre los sub-vectores.$\frac{512}{64} = 8$

Cual es el resultado?

Detuvimos nuestros experimentos en el índice "IVF262144, PQ64", ya que satisfizo completamente todas nuestras necesidades de velocidad y precisión de búsqueda, y también aseguró el uso razonable del espacio en disco con una mayor escala del índice. Más específicamente, en este momento, con 315 millones de vectores, el índice ocupa 22 GB de espacio en disco y aproximadamente 3 GB de RAM cuando se usa.



Otro detalle interesante que no mencionamos anteriormente es la métrica utilizada por el índice. Por defecto, las distancias entre dos vectores se consideran en la métrica euclidiana L2, o en un lenguaje más comprensible, las distancias se consideran como la raíz cuadrada de la suma de los cuadrados de las diferencias de coordenadas. Pero puede establecer otra métrica, en particular, probamos la métrica METRIC_INNER_PRODUCT, o la métrica de las distancias del coseno entre vectores. Es coseno porque el coseno del ángulo entre dos vectores en el sistema de coordenadas euclidiana se expresa como la relación del producto escalar (en coordenadas) al producto de sus longitudes, y si todos los vectores en nuestro espacio tienen longitud 1, entonces el coseno del ángulo será exactamente igual al producto en forma de coordenadas. En este caso, cuanto más cerca estén los vectores en el espacio, más cerca de uno estará su producto de punto.



La métrica L2 tiene una transición matemática directa a la métrica del producto punto. Sin embargo, al comparar experimentalmente las dos métricas, la impresión fue que la métrica de los productos escalares nos ayuda a analizar los coeficientes de similitud de las imágenes de una manera más exitosa. Además, las incrustaciones de nuestras fotos se obtuvieron utilizandoInsightFace , que implementa la arquitectura ArcFace utilizando distancias de coseno. También hay otras métricas en los índices FAISS que puede leer aquí .

Conclusión y ejemplos interesantes.

Entonces, de vuelta a donde todo comenzó. Y comenzó, recuerde, con la motivación de resolver el problema de encontrar bots en la red de Instagram y, más específicamente, buscar publicaciones duplicadas con personas o avatares en ciertos grupos de usuarios. En el proceso de redacción del material, quedó claro que una descripción detallada de nuestra metodología de búsqueda de bots se dibuja en un artículo separado, que discutiremos en futuras publicaciones, pero por ahora nos limitaremos a ejemplos de nuestros experimentos con FAISS.



Puede vectorizar imágenes o caras de diferentes maneras, elegimos la tecnología InsightFace (vectorizar imágenes y seleccionar características n-dimensionales de ellas es una larga historia separada). En el curso de los experimentos con la infraestructura que recibimos, se descubrieron propiedades bastante interesantes y divertidas.



Por ejemplo, con el permiso de colegas y conocidos, subimos sus rostros en una búsqueda y rápidamente encontramos las fotos en las que están presentes:





nuestro colega se metió en la foto de un visitante de la Comic-Con, estando en segundo plano en la multitud. Fuente





Picnic en un gran grupo de amigos, foto de la cuenta de un amigo. Fuente





Simplemente pasando. Un fotógrafo desconocido capturó a los chicos por su perfil temático. No sabían dónde había terminado su foto, y después de 5 años olvidaron por completo cómo fueron fotografiados. Fuente





En este caso, el fotógrafo es desconocido y fotografiado en secreto.

Inmediatamente recordé a una chica sospechosa con una cámara réflex, sentada enfrente en ese momento :) Fuente



Por lo tanto, mediante acciones simples, FAISS le permite ensamblar un análogo del conocido FindFace en su rodilla.



Otra característica interesante: en el índice FAISS, cuanto más se parecen las caras entre sí, más cerca están los vectores correspondientes en el espacio. Decidí mirar más de cerca los resultados de búsqueda un poco menos precisos en mi cara y encontré clones terriblemente similares a mí :)





Algunos de los clones del autor.

Fuentes fotográficas: 1 , 2 ,  3



En general, FAISS abre un campo enorme para la implementación de cualquier idea creativa. Por ejemplo, usando el mismo principio de proximidad vectorial de caras similares, uno podría construir caminos de una persona a otra. O, como último recurso, haga de FAISS una fábrica para la producción de tales memes:





Fuente ¡



Gracias por su atención y esperamos que este material sea útil para los lectores de Habr!



Este artículo fue escrito con el apoyo de mis colegas Artyom Korolyov (korolevart), Timur Kadyrov y Arina Reshetnikova.



I + D Dentsu Aegis Network Rusia.