Continuamos familiarizándonos con una variedad de montones y algoritmos de clasificación utilizando estos montones. Hoy tenemos el llamado árbol de torneos.
La idea principal de la clasificación de torneos es usar un montón auxiliar relativamente pequeño (en comparación con la matriz principal), que actúa como una cola prioritaria. En este montón, se comparan los elementos en los niveles más bajos, como resultado de lo cual los elementos más pequeños (en este caso, el árbol MIN-HEAP) suben, y el mínimo actual de la parte de los elementos de la matriz que caen en este montón aparece en la raíz. El mínimo se transfiere a una matriz adicional de "ganadores", como resultado de lo cual el montón compara / mueve los elementos restantes, y ahora hay un nuevo mínimo en la raíz del árbol. Tenga en cuenta que con un sistema de este tipo, el siguiente mínimo es mayor en valor que el anterior; luego, se ensambla fácilmente una nueva matriz ordenada de "ganadores", donde simplemente se agregan nuevos mínimos al final de la matriz adicional.
EDISON .
, . , .
computer science ;-)
Mover los mínimos a una matriz adicional lleva al hecho de que aparecen vacantes en el montón para los siguientes elementos de la matriz principal, como resultado de lo cual todos los elementos se procesan en el orden de la cola.
La principal sutileza es que además de los "ganadores" también hay "perdedores". Si algunos elementos ya se han transferido al conjunto de "ganadores", entonces si los elementos no procesados son más pequeños que estos "ganadores", entonces no tiene sentido separarlos a través del árbol del torneo en esta etapa; insertar estos elementos en el conjunto de "ganadores" será demasiado costoso (en No puede finalizarlos, pero para ponerlos al principio, debe cambiar los mínimos previamente insertados). Dichos elementos que no lograron encajar en el conjunto de "ganadores" se envían al conjunto de "perdedores": pasarán por el árbol del torneo en una de las siguientes iteraciones, cuando todas las acciones se repitan para los perdedores restantes.
No es fácil encontrar una implementación de este algoritmo en Internet, pero se encontró una implementación clara y agradable en Ruby en YouTube. El código Java también se menciona en la sección "Enlaces", pero no parece tan legible allí.
#
require_relative "pqueue"
#
MAX_SIZE = 16
def tournament_sort(array)
# , ""
return optimal_tourney_sort(array) if array.size <= MAX_SIZE
bracketize(array) # , ""
end
#
def bracketize(array)
size = array.size
pq = PriorityQueue.new
#
pq.add(array.shift) until pq.size == MAX_SIZE
winners = [] # ""
losers = [] # ""
#
until array.empty?
# "" ?
if winners.empty?
# ""
winners << pq.peek
#
pq.remove
end
# , ""
if array.first > winners.last
pq.add(array.shift) #
else # ""
losers << array.shift # ""
end
# , ""
winners << pk.peek unless pk.peek.nil?
pq.remove #
end
# , - ?
until pq.heap.empty?
winners << pq.peek # ""
pq.remove #
end
# "" , , ,
# "" -
return winners if losers.empty?
# , ""
# ""
array = losers + winners
array.pop while array.size > size
bracketize(array) #
end
#
def optimal_tourney_sort(array)
sorted_array = [] #
pq = PriorityQueue.new
array.each { |num| pq.add(num) } # -
until pq.heap.empty? # -
sorted_array << pq.heap[0]
pq.remove #
end
sorted_array #
end
#
if $PROGRAM_NAME == __FILE__
#
shuffled_array = Array.new(30) { rand(-100 ... 100) }
#
puts "Random Array: #{shuffled_array}"
#
puts "Sorted Array: #{tournament_sort(shuffled_array)}"
endEsta es una implementación ingenua, en la que después de cada división en "perdedores" y "ganadores", estos conjuntos se combinan y luego, para el conjunto combinado, todas las acciones se repiten nuevamente. Si en la matriz combinada hay elementos "perdedores" primero, luego examinar el montón de torneos los ordenará junto con los "ganadores".
Esta implementación es bastante simple e intuitiva, pero no se puede llamar efectiva. Los "ganadores" ordenados pasan varias veces por el árbol del torneo, lo que obviamente es redundante. Supongo que la complejidad del tiempo aquí es log-cuadrática,
Opción de combinación de múltiples rutas
El algoritmo se acelera notablemente si los elementos ordenados que pasan por el tamiz no se pasan repetidamente por las carreras del torneo.
Después de que la matriz desordenada se divide en "ganadores" ordenados y "perdedores" sin clasificar, todo el proceso se repite solo para los "perdedores". En cada nueva iteración, se acumulará un conjunto de matrices con "ganadores" y esto continuará hasta que en algún momento no queden "perdedores". Después de eso, todo lo que queda es fusionar todas las matrices de "ganadores". Como todas estas matrices están ordenadas, esta fusión se realiza con un mínimo esfuerzo.
De esta forma, el algoritmo ya puede encontrar una aplicación útil. Por ejemplo, si tiene que trabajar con big data, a lo largo del proceso de uso del montón de torneos, se lanzarán paquetes de datos ordenados con los que ya puede hacer algo mientras se procesa todo lo demás.
Cada uno de los n elementos de la matriz pasa por el árbol de torneos solo una vez, lo que lleva tiempo
En el final de temporada
Una serie de artículos sobre la clasificación del montón está casi completa. Queda por hablar sobre el más efectivo de ellos.
Enlaces
Tournament sort
Priority queue
Tournament sort in Java
The Theory Behind the The Theory Behind the z/Architecture Sort Assist Instructions
Using Tournament Trees to Sort
Tournament Sort Demo Ruby
Tournament Sort Visualization
Tournament Sort Data Structure UGC NET DS
Tournament Sort Algorithm — a Heapsort variant
:
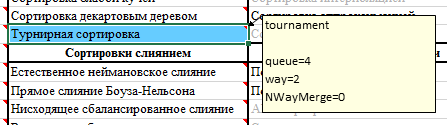
La clasificación de hoy se ha agregado a la aplicación AlgoLab, que la usa: actualice el archivo de Excel con macros.
En los comentarios a la celda con el nombre de clasificación, puede especificar algunas configuraciones.
La forma variable es un árbol de torneo de múltiples vías (por si acaso, es posible hacer que este árbol no solo sea binario, sino también ternario, cuaternario y pentario).
La variable de cola es el tamaño de la cola inicial (el número de nodos en el nivel más bajo del árbol). Como los árboles están llenos, si, por ejemplo, con way = 2, especifique cola = 5, entonces el tamaño de la cola aumentará a la potencia más cercana de dos (en este caso, hasta 8).
Variable NWayMerge toma el valor 1 o 0; con la ayuda de este se indica si se debe usar la combinación de múltiples rutas o no.