👱🏿 👨🏼‍🍳 👂🏽 Aplicación obscena ⌨️ 🚡 👌🏿

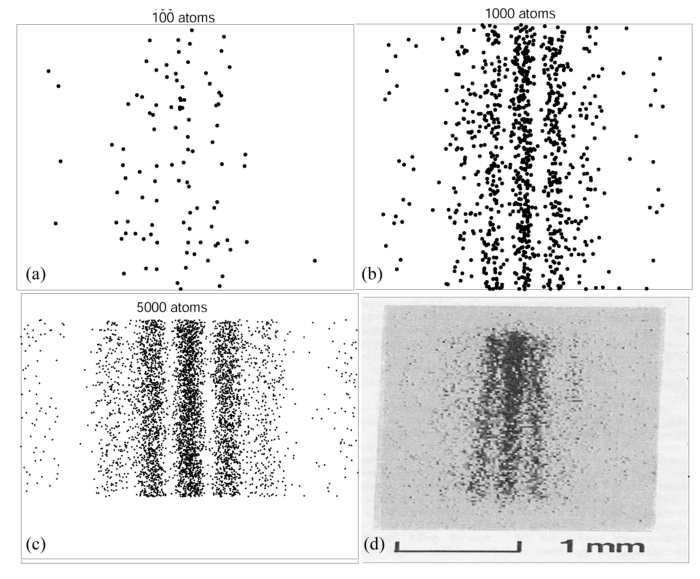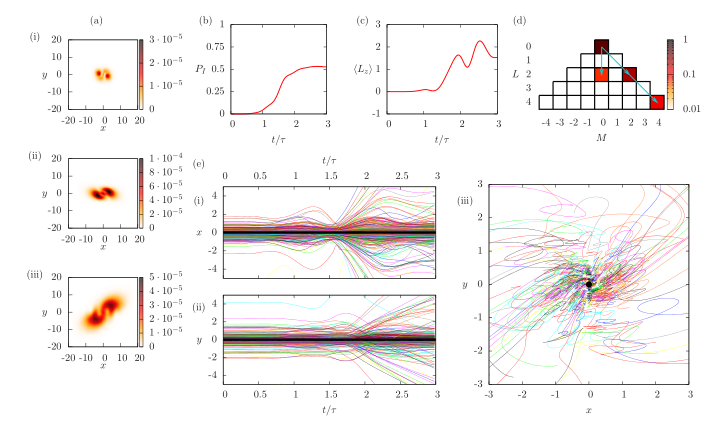
En el apéndice del artículo, el camino de la partícula proporciona materiales cortados: integrales del camino, un experimento de dos huecos en átomos de neón fríos, marcos de teletransportación de partículas y otras escenas de crueldad y naturaleza sexual.

En mi opinión, no puede haber otra forma de considerar el formalismo matemático como lógicamente coherente que demostrar que sus consecuencias se desvían de la experiencia, o demostrar que sus predicciones no agotan las posibilidades de observación.

Niels Bohr

En conclusión, el autor quisiera afirmar que reconocemos solo dos buenas razones para rechazar una teoría que explica una amplia gama de fenómenos. En primer lugar, la teoría no es internamente consistente y, en segundo lugar, no está de acuerdo con los experimentos.

David Bohm

Anteriormente aprendimos de dónde viene la ecuación de Schrödinger, por qué se toma de allí y cómo se toma por varios métodos

i ℏ \frac{\partial Ψ}{\partial t} = (- \frac{ℏ^{2}}{2 m} \nabla^{2} + V) Ψ

$i\hbar\frac{\partial\Psi}{\partial t} = \left( -\frac{\hbar^2}{2m}\nabla^2 + V\right) \Psi$

Ahora, lo dividimos en dos ecuaciones reales. Para hacer esto, representamos psi en forma polar $\Psi = Re^{iS/\hbar}$ , :

\frac{\partial S}{\partial t} + \frac{(\nabla S)^{2}}{2 m} - \frac{ℏ^{2}}{2 m} \frac{\nabla^{2} R}{R} + V = 0 \frac{\partial R^{2}}{\partial t} + \nabla \cdot (\frac{R^{2} \nabla S}{m}) = 0

$\frac{\partial S}{\partial t}+\frac{(\nabla S)^{2}}{2 m}-\frac{\hbar^{2}}{2 m} \frac{\nabla^{2} R}{R}+V=0 \\ \frac{\partial R^{2}}{\partial t}+\nabla \cdot\left(\frac{R^{2} \nabla S}{m}\right)=0$

S — , R — . , , , — -, ( ).

, $U = \nabla S /m$ . , S -, - - :

S = - \frac{i ℏ}{2} \ln \frac{Ψ}{Ψ^{*}}

$S = -\frac{i\hbar}{2}\ln\frac{\Psi}{\Psi^*}$

, -, , , , S, , , , . , , . -.

— , . , , , . , , , .

, , , . . . , , , .

, .

, , , . , ( - ). :

()

, , , : ,

, . . .

U = \nabla S / m = - \frac{i ℏ}{2 m} \nabla \ln \frac{Ψ}{Ψ^{*}} = \frac{ℏ}{m} I m (\frac{\nabla ψ}{ψ})

$U = \nabla S /m = -\frac{i\hbar}{2m}\nabla\ln\frac{\Psi}{\Psi^*} = \frac{\hbar}{m}\mathrm{Im}\left(\frac{\nabla\psi}{\psi} \right)$

-, :

x + = U Δ t

$x += U\Delta t$

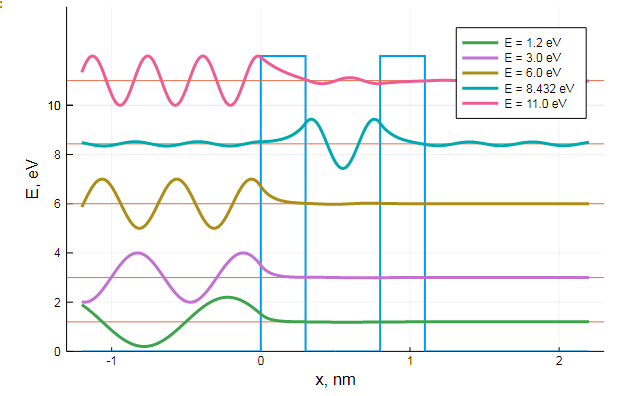
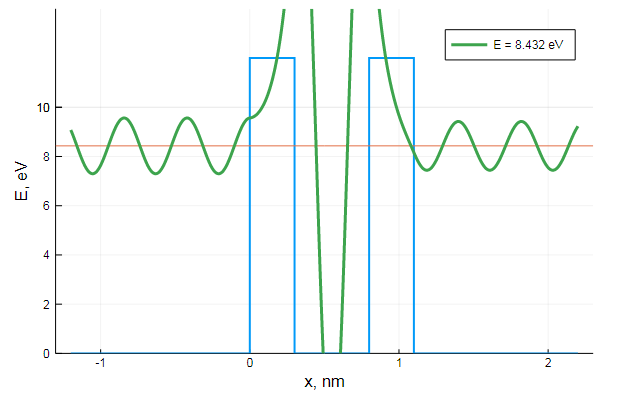
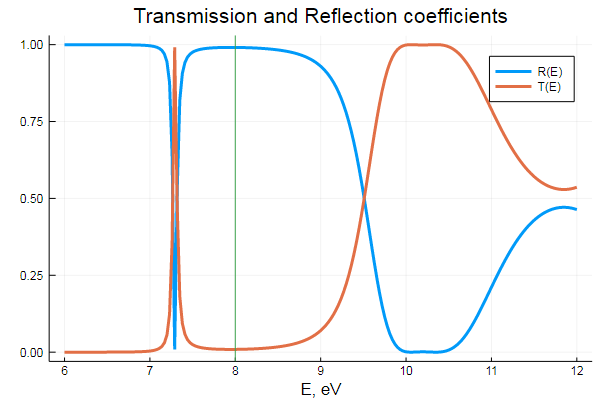
using LinearAlgebra, SparseArrays, Plots

const ħ = 1.0546e-34 # J*s
const m = 9.1094e-31 # kg
const q = 1.6022e-19 # Kl
const nm = 1e-9 # m
const fs = 1e-12; # s

function wavefun()

    gauss(x) = exp( -(x-x0)^2 / (2*σ^2) + im*x*k )
    k = m*v/ħ

    #    
    Vm = spdiagm(0 => V )
    H = spdiagm(-1 => ones(Nx-1), 0 => -2ones(Nx), 1 => ones(Nx-1) )
    H *= ħ^2 / ( 2m*dx^2 )
    H += Vm

    A = I + 0.5im*dt/ħ * H #  
    B = I - 0.5im*dt/ħ * H # 
    psi = zeros(Complex, Nx, Nt)
    psi[:,1] = gauss.(x)

    for t = 1:Nt-1

        b = B * psi[:,t]
        #       A*psi = b
        psi[:,t+1] = A \ b
    end

    return psi
end

dx = 0.05nm # x step
dt = 0.01fs # t step
xlast = 400nm
Nt = 260 # Number of time steps
t = range(0, length = Nt, step = dt)

x = [0:dx:xlast;]
Nx = length(x) # Number of spatial steps

a1 = 200nm
a2 = 200.5nm # 5 
a3 = 205nm
a4 = 205.5nm 
#V = [ a1<xi<a2 ? 2q : 0.0 for xi in x ] # 2 eV 
V = [ a1<xi<a2 || a3<xi<a4 ? 2q : 0.0 for xi in x ] # 2 eV 

x0 = 80nm # Initial position
σ = 20nm # gauss width
v = -120nm/fs;

@time Psi = wavefun()
P = abs2.(Psi);

function ψ(xi, j)

    k = findfirst(el-> abs(el-xi)<dx, x)
    k == nothing && ( k = 1 )

    Psi[k, j]
end

function corpusculaz(n)

    X = zeros(n, Nt)
    X[:,1] = x0 .+ σ*randn(n)

    for j in 2:Nt, i in 1:n
        U = ħ/(2m*dx) * imag( ( ψ(X[i,j-1]+dx, j) -  ψ(X[i,j-1]-dx, j) ) /  ψ(X[i,j-1], j) )
        X[i,j] = X[i,j-1] - U*dt
    end

    X
end

@time X = corpusculaz(20);

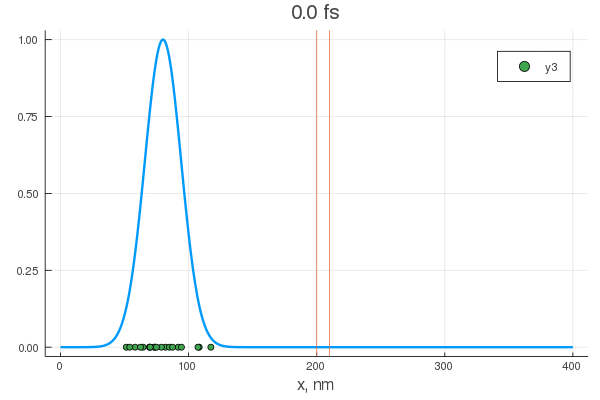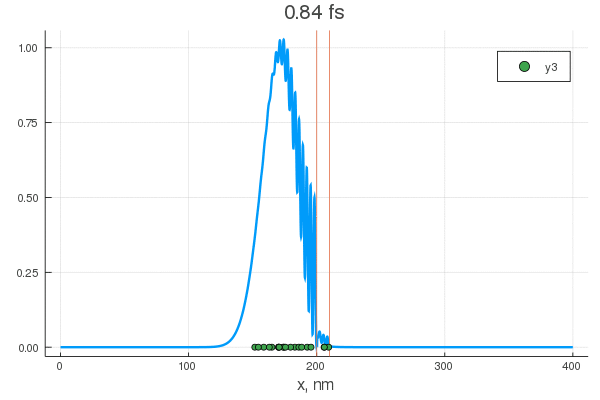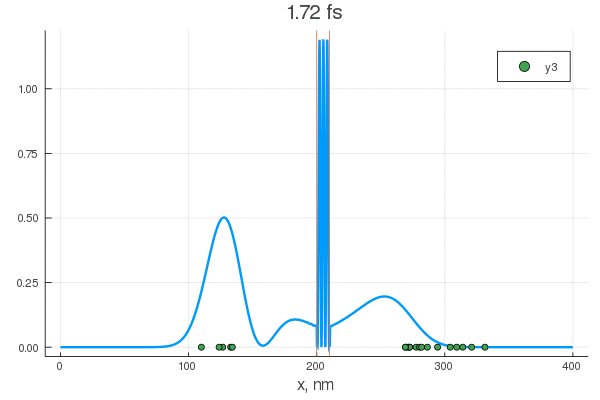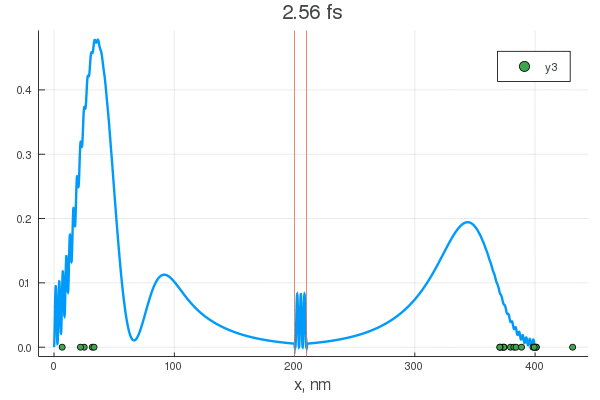
plot(x, P[:, 1], legend = false)
plot!(x, P[:, 80], legend = false)
scatter!( X[:,1], zeros(20) )
scatter!( X[:,80], zeros(20) )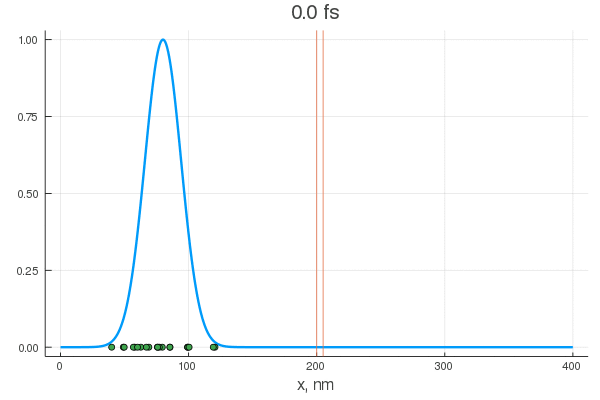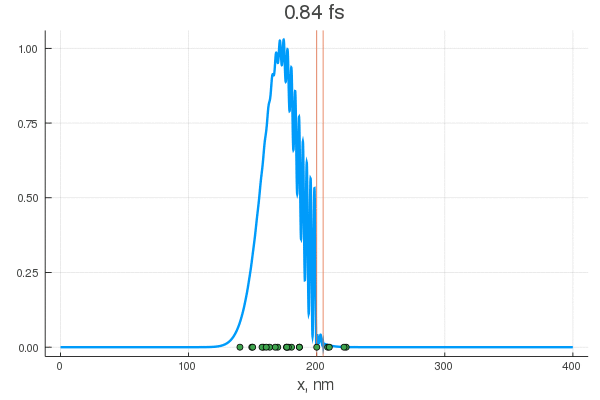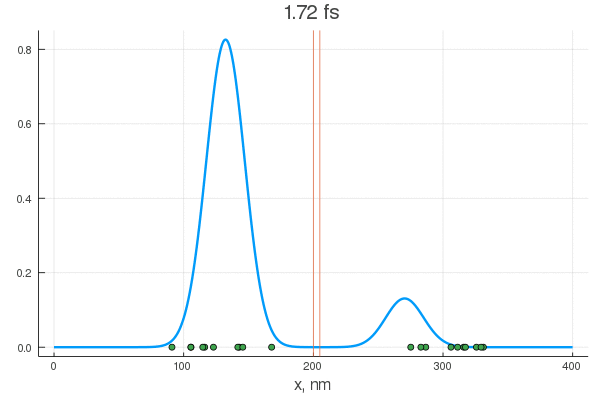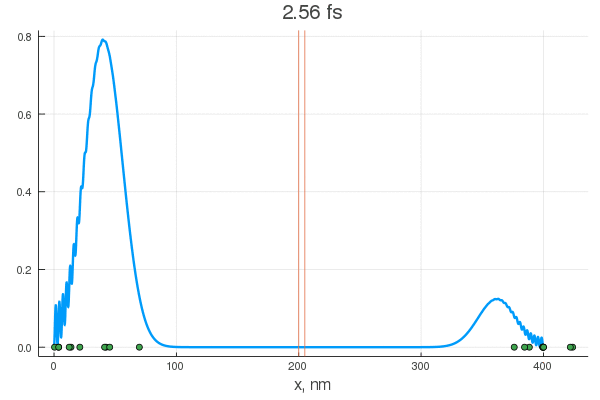

. — , . :

, . , , !

, . Double-slit interference with ultracold metastable neon atoms — - .

using Random, Gnuplot, Statistics
#  
function trapez(f, a, b, n)
    h = (b - a)/n
    result = 0.5*(f(a) + f(b))
    for i in 1:n-1
        result += f(a + i*h)
    end
    result * h
end
#  
function rk4(f, x, y, h)
    k1 = h * f(x       , y        )
    k2 = h * f(x + 0.5h, y + 0.5k1)
    k3 = h * f(x + 0.5h, y + 0.5k2)
    k4 = h * f(x +    h, y +    k3)

    return y + (k1 + 2*(k2 + k3) + k4)/6.0
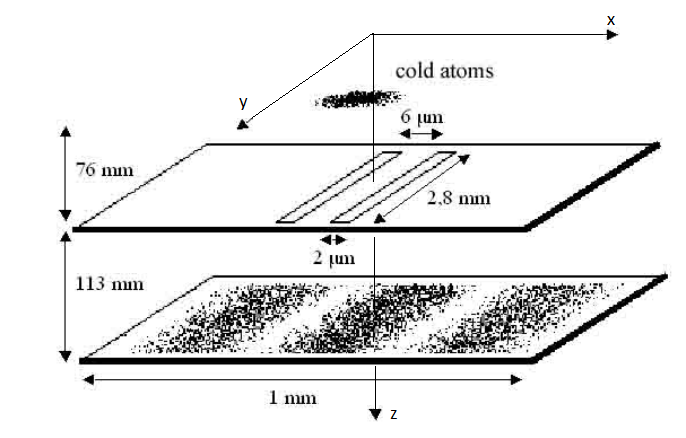
end

const ħ = 1.055e-34 # J*s 
const kB = 1.381e-23 # J*K-1
const g = 9.8 # m/s^2

const l1 = 76e-3 # m
const l2 = 113e-3 # m
const yh = 2.8e-3 # m
const d = 6e-6 # m
const b = 2e-6 # m
const a1 = 0.5(- d - b) # 
const a2 = 0.5(- d + b)
const b1 = 0.5(  d - b)
const b2 = 0.5(  d + b)

const m = 3.349e-26 # kg
const T = 2.5e-3 # K
const σv = sqrt(kB*T/m) #  
const σ₀ = 10e-6 # 10 mkm #      
const σz = 3e-4 # 0.3 mm #  z
const σk = m*σv / (ħ*√3) # 2e8 m/s #    

v₀ = zeros(3)
k₀ = zeros(3);

: , , -, .

\begin{aligned} 1) ψ_{0} (x, y, z; k_{0 x}, k_{0 y}, k_{0 z}) = & ψ_{0 x} (x; k_{0 x}) ψ_{0_{y}} (z; k_{0 y}) ψ_{0 z} (z; k_{0 z}) \\ = & {(2 π σ_{0}^{2})}^{- 1 / 4} e^{- x^{2} / 4 σ_{0}^{2}} e^{i k_{0 x} x} \\ \times {(2 π σ_{0}^{2})}^{- 1 / 4} e^{- y^{2} / 4 σ_{0}^{2}} e^{i k_{0 y} y} \\ \times {(2 π σ_{z}^{2})}^{- 1 / 4} e^{- z^{2} / 4 σ_{z}^{2}} e^{i k_{0 z} z} \end{aligned}

$\begin{aligned} 1)\psi_{0}\left(x, y, z ; k_{0 x}, k_{0 y}, k_{0 z}\right)=& \psi_{0 x}\left(x ; k_{0 x}\right) \psi_{0_{y}}\left(z ; k_{0 y}\right) \psi_{0 z}\left(z ; k_{0 z}\right) \\ =&\left(2 \pi \sigma_{0}^{2}\right)^{-1 / 4} e^{-x^{2} / 4 \sigma_{0}^{2}} e^{i k_{0 x} x} \\ & \times\left(2 \pi \sigma_{0}^{2}\right)^{-1 / 4} e^{-y^{2} / 4 \sigma_{0}^{2}} e^{i k_{0 y} y} \\ & \times\left(2 \pi \sigma_{z}^{2}\right)^{-1 / 4} e^{-z^{2} / 4 \sigma_{z}^{2}} e^{i k_{0 z} z} \end{aligned}$

, . , , , . , , .

, . , , — . , , , . , , .

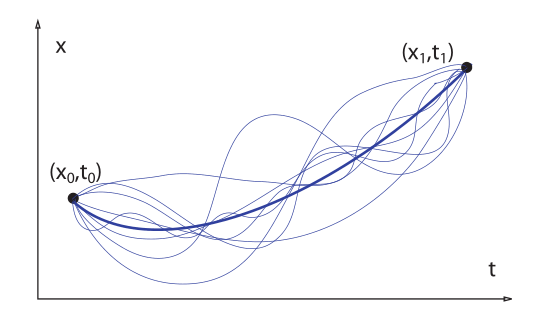
Quantum Mechanics And Path Integrals, A. R. Hibbs, R. P. Feynman, , 3.6 .

K (β, t_{β}; α, t_{α}) = K_{x} (x_{β}, t_{β}; x_{α}, t_{α}) K_{y} (y_{β}, t_{β}; y_{α}, t_{α}) K_{z} (z_{β}, t_{β}; z_{α}, t_{α})

$K\left(\beta, t_{\beta} ; \alpha, t_{\alpha}\right)=K_{x}\left(x_{\beta}, t_{\beta} ; x_{\alpha}, t_{\alpha}\right) K_{y}\left(y_{\beta}, t_{\beta} ; y_{\alpha}, t_{\alpha}\right) K_{z}\left(z_{\beta}, t_{\beta} ; z_{\alpha}, t_{\alpha}\right)$

\begin{aligned} K_{x} (x_{β}, t_{β}; x_{α}, t_{α}) = & {(\frac{m}{2 i π ℏ (t_{β} - t_{α})})}^{1 / 2} \exp \frac{i m}{ℏ} (\frac{{(x_{β} - x_{α})}^{2}}{2 (t_{β} - t_{α})}) \\ K_{y} (y_{β}, t_{β}; y_{α}, t_{α}) = & {(\frac{m}{2 i π ℏ (t_{β} - t_{α})})}^{1 / 2} \exp \frac{i m}{ℏ} (\frac{{(y_{β} - y_{α})}^{2}}{2 (t_{β} - t_{α})}) \\ K_{z} (z_{β}, t_{β}; z_{α}, t_{α}) = & {(\frac{m}{2 i π ℏ (t_{β} - t_{α})})}^{1 / 2} \exp \frac{i m}{ℏ} (\frac{{(z_{β} - z_{α})}^{2}}{2 (t_{β} - t_{α})}) \\ \times \exp \frac{i m}{ℏ} (\frac{g}{2} (z_{β} + z_{α}) (t_{β} - t_{α}) - \frac{g^{2}}{24} {(t_{β} - t_{α})}^{3}) \end{aligned}

$\begin{aligned} K_{x}\left(x_{\beta}, t_{\beta} ; x_{\alpha}, t_{\alpha}\right)=&\left(\frac{m}{2 i \pi \hbar\left(t_{\beta}-t_{\alpha}\right)}\right)^{1 / 2} \exp \frac{i m}{\hbar}\left(\frac{\left(x_{\beta}-x_{\alpha}\right)^{2}}{2\left(t_{\beta}-t_{\alpha}\right)}\right) \\ K_{y}\left(y_{\beta}, t_{\beta} ; y_{\alpha}, t_{\alpha}\right)=&\left(\frac{m}{2 i \pi \hbar\left(t_{\beta}-t_{\alpha}\right)}\right)^{1 / 2} \exp \frac{i m}{\hbar}\left(\frac{\left(y_{\beta}-y_{\alpha}\right)^{2}}{2\left(t_{\beta}-t_{\alpha}\right)}\right) \\ K_{z}\left(z_{\beta}, t_{\beta} ; z_{\alpha}, t_{\alpha}\right)=&\left(\frac{m}{2 i \pi \hbar\left(t_{\beta}-t_{\alpha}\right)}\right)^{1 / 2} \exp \frac{i m}{\hbar}\left(\frac{\left(z_{\beta}-z_{\alpha}\right)^{2}}{2\left(t_{\beta}-t_{\alpha}\right)}\right) \\ & \times \exp \frac{i m}{\hbar}\left(\frac{g}{2}\left(z_{\beta}+z_{\alpha}\right)\left(t_{\beta}-t_{\alpha}\right)-\frac{g^{2}}{24}\left(t_{\beta}-t_{\alpha}\right)^{3}\right) \end{aligned}$

Z , . ,

ψ (β, t) = \int K (β, t; α, t_{α}) ψ (α, t_{α}) d x_{α}, d y_{α}, d z_{α}

$\psi\left(\beta, t \right)=\int K\left(\beta, t ; \alpha, t_{\alpha}\right) \psi\left(\alpha, t_{\alpha}\right) d x_{\alpha}, d y_{\alpha}, d z_{\alpha}$

, . , X, . :

\begin{aligned} ψ_{x} (x, t; k_{0 x}) & = \int K (x, t; x_{α}, 0) ψ_{0} (x_{α}) d x_{α} \\ ψ_{x} (x, t; k_{0 x}) & = {(2 π s_{0}^{2} (t))}^{- 1 / 4} \exp [- \frac{{(x - v_{0 x} t)}^{2}}{4 σ_{0} s_{0} (t)} + i k_{0 x} (x - v_{0 x} t)] \\ ρ_{x} (x, t) & = {(2 π ε_{0}^{2} (t))}^{- 1 / 2} \exp [- \frac{x^{2}}{2 ε_{0}^{2} (t)}] \end{aligned}

$\begin{aligned} \psi_{x}\left(x, t ; k_{0 x}\right)&=\int K\left(x, t ; x_\alpha, 0\right) \psi_0\left(x_\alpha\right) d x_{\alpha}\\ \psi_{x}\left(x, t ; k_{0 x}\right) &=\left(2 \pi s_{0}^{2}(t)\right)^{-1 / 4} \exp \left[-\frac{\left(x-v_{0 x} t\right)^{2}}{4 \sigma_{0} s_{0}(t)}+i k_{0 x}\left(x-v_{0 x} t\right)\right] \\ \rho_{x}(x, t) &=\left(2 \pi \varepsilon_{0}^{2}(t)\right)^{-1 / 2} \exp \left[-\frac{x^{2}}{2 \varepsilon_{0}^{2}(t)}\right] \end{aligned}$

ε_{0}^{2} (t) = σ_{0}^{2} (t) + {(\frac{h t σ_{v}}{m})}^{2} σ_{0}^{2} (t) = σ_{0}^{2} + {(\frac{h t}{2 m σ_{0}^{2}})}^{2}

$\varepsilon_{0}^{2}(t)=\sigma_{0}^{2}(t)+\left(\frac{h t \sigma_v}{m}\right)^{2}\\ \sigma_{0}^{2}(t)=\sigma_{0}^{2}+\left(\frac{h t}{2 m \sigma_{0}^{2}}\right)^{2}$

, :

ε₀(t) = σ₀^2 + ( ħ/(2m*σ₀) * t )^2 + (ħ*t*σv/m)^2
s₀(t) = σ₀ + im*ħ/(2m*σ₀) * t

ρₓ(x, t) = exp( -x^2 / (2ε₀(t)) ) / sqrt( 2π*ε₀(t) )

t₁(v, z) = sqrt( 2*(l1-z)/g + (v/g)^2 ) - v/g
tf1 = t₁(v₀[3], 0) # s #    
X1 = range(-100, stop = 100, length = 100)*1e-6 
Z1 = range(0, stop = l1, length = 100)
Cron1 = range(0, stop = tf1, length = 100)

P1 = [ ρₓ(x, t) for t in Cron1, x in X1 ]
P1 /= maximum(P1); #   

@gp "set title 'Wavefun before the slits'" xlab="Z, mkm" ylab="X, mkm"
@gp :- 1000Z1 1000000X1 P1 "w image notit"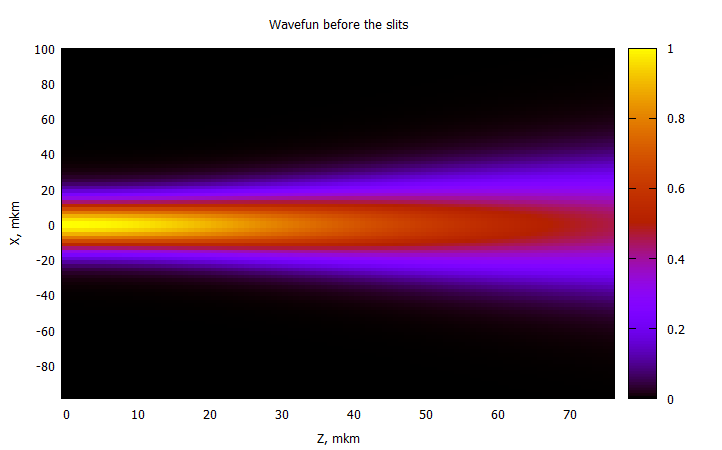

— .

, :

\begin{aligned} ψ_{x} & (x, t) = ψ_{A} + ψ_{B} \\ ψ_{A} & = \int_{A} K_{x} (x, t; x_{a}, t_{1}) ψ_{x} (x_{a}, t_{1}, k_{0 x}) d x_{a} \\ ψ_{B} & = \int_{B} K_{x} (x, t; x_{b}, t_{1}) ψ_{x} (x_{b}, t_{1}, k_{0 x}) d x_{b} \end{aligned}

$\begin{aligned} \psi_{x}&\left(x, t\right)=\psi_{A}+\psi_{B}\\ \psi_{A} &=\int_{A} K_{x}\left(x, t ; x_{a}, t_{1}\right) \psi_{x}\left(x_{a}, t_{1}, k_{0 x}\right) d x_{a} \\ \psi_{B} &=\int_{B} K_{x}\left(x, t ; x_{b}, t_{1}\right) \psi_{x}\left(x_{b}, t_{1}, k_{0 x}\right) d x_{b} \end{aligned}$

ρ_{x} (x, t) = \int_{- \infty}^{+ \infty} {(2 π σ_{v}^{2})}^{- 1 / 2} \exp (- \frac{k_{0 x}^{2}}{2 σ_{v}^{2}}) {| ψ_{x} (x, t; k_{0 x}) |}^{2} d k_{0 x}

$\rho_{x}\left(x, t\right)=\int_{-\infty}^{+\infty}\left(2 \pi \sigma_v^{2}\right)^{-1 / 2} \exp \left(-\frac{k_{0 x}^{2}}{2 \sigma_v^{2}}\right)\left|\psi_{x}\left(x, t ; k_{0 x}\right)\right|^{2} d k_{0 x}$

, :

function ρₓ(xᵢ, tᵢ) 

    Kₓ(xb, tb, xa, ta) = sqrt( m/(2im*π*ħ*(tb-ta)) ) * exp( im*m*(xb-xa)^2 / (2ħ*(tb-ta)) )

    function subintrho(k) 

        ψₓ(x, t) = ( 2π*s₀(t) )^-0.25 * exp( -(x-ħ*k*t/m)^2 / (4σ₀*s₀(t)) + im*k*(x-ħ*k*t/m) )
        subintpsi(x) = Kₓ(xᵢ, tᵢ, x, tf1) * ψₓ(x, tf1)

        ψa = trapez(subintpsi, a1, a2, 200)
        ψb = trapez(subintpsi, b1, b2, 200)

        exp( -k^2 / (2σv^2) ) * abs2(ψa + ψb)
    end

    trapez(subintrho, -10σk, 10σk, 20) / sqrt( 2π*σv^2 )
end

t₂(v, z) = sqrt( 2*(l1+l2-z)/g + (v/g)^2 ) - v/g
tf2 = t₂(v₀[3], 0) # s #    
X2 = range(-800, stop = 800, length = 200)*1e-6
Z2 = range(l1, stop = l2, length = 100)
Cron2 = range(tf1, stop = tf2, length = 100)

@time P2 = [ ρₓ(x, t) for t in Cron2, x in X2 ];

P2 /= maximum(P2[4:end,:]);
@gp "set title 'Wavefun after the slits'" xlab="t, s" ylab="X, mkm"
@gp :- Cron2[4:end] 1000000X2 P2[4:end,:] "w image notit"

2 :

\vec{v} = \frac{\nabla S}{m}

$\vec v = \frac{\nabla S}{m}$

. . , ,

\begin{aligned} \vec{v} (x, y, z, t) & = \frac{\nabla S}{m} + \frac{\nabla \log ρ \times \vec{s}}{m} \\ \vec{s} & = (0, 0, ℏ / 2) \\ \frac{\nabla \log ρ \times \vec{s}}{m} & = \frac{ℏ}{2 m ρ} (\frac{\partial ρ}{\partial y}, - \frac{\partial ρ}{\partial x}, 0) \end{aligned}

$\begin{aligned} \vec v(x, y, z, t)&=\frac{\nabla S}{m}+\frac{\nabla \log \rho \times \vec s}{m} \\ \vec s &= (0,0,\hbar/2)\\ \frac{\nabla \log \rho \times \vec s}{m} &= \frac{\hbar}{2 m \rho}\left( \frac{\partial \rho}{\partial y}, -\frac{\partial \rho}{\partial x}, 0\right) \end{aligned}$

, ,

\begin{aligned} \frac{d x}{d t} & = v_{x} (x, t) = \frac{1}{m} \frac{\partial S}{\partial x} + \frac{ℏ}{2 m ρ} \frac{\partial ρ}{\partial y} = v_{0 x} + \frac{(x - v_{0 x} t) ℏ^{2} t}{4 m^{2} σ_{0}^{2} σ_{0}^{2} (t)} - \frac{ℏ (y - v_{0 y} t)}{2 m σ_{0}^{2} (t)} \\ \frac{d y}{d t} & = v_{y} (x, t) = \frac{1}{m} \frac{\partial S}{\partial y} - \frac{ℏ}{2 m ρ} \frac{\partial ρ}{\partial x} = v_{0 y} - \frac{(y - v_{0 y} t) ℏ^{2} t}{4 m^{2} σ_{0}^{2} σ_{0}^{2} (t)} + \frac{ℏ (x - v_{0 x} t)}{2 m σ_{0}^{2} (t)} \\ \frac{d z}{d t} & = v_{z} (z, t) = \frac{1}{m} \frac{\partial S}{\partial z} = v_{0 z} + g t + \frac{(z - v_{0 z} t - g t^{2} / 2) ℏ^{2} t}{4 m^{2} σ_{z}^{2} σ_{z}^{2} (t)} \end{aligned}

$\begin{aligned} \frac{d x}{d t} &=v_{x}(x, t)=\frac{1}{m} \frac{\partial S}{\partial x}+\frac{\hbar}{2 m \rho} \frac{\partial \rho}{\partial y}=v_{0 x}+\frac{\left(x-v_{0 x} t\right) \hbar^{2} t}{4 m^{2} \sigma_{0}^{2} \sigma_{0}^{2}(t)}-\frac{\hbar\left(y-v_{0 y} t\right)}{2 m \sigma_{0}^{2}(t)} \\ \frac{d y}{d t} &=v_{y}(x, t)=\frac{1}{m} \frac{\partial S}{\partial y}-\frac{\hbar}{2 m \rho} \frac{\partial \rho}{\partial x}=v_{0 y}-\frac{\left(y-v_{0 y} t\right) \hbar^{2} t}{4 m^{2} \sigma_{0}^{2} \sigma_{0}^{2}(t)}+\frac{\hbar\left(x-v_{0 x} t\right)}{2 m \sigma_{0}^{2}(t)} \\ \frac{d z}{d t} &= v_{z}(z, t)=\frac{1}{m} \frac{\partial S}{\partial z}=v_{0 z}+g t+\frac{\left(z-v_{0 z} t-g t^{2} / 2\right) \hbar^{2} t}{4 m^{2} \sigma_{z}^{2} \sigma_{z}^{2}(t)} \end{aligned}$

\begin{aligned} x (t) & = v_{0 x} t + \sqrt{x_{0}^{2} + y_{0}^{2}} \frac{σ_{0} (t)}{σ_{0}} \cos φ (t) \\ y (t) & = v_{0 y} t + \sqrt{x_{0}^{2} + y_{0}^{2}} \frac{σ_{0} (t)}{σ_{0}} \sin φ (t) \\ z (t) & = v_{0 z} t + \frac{1}{2} g t^{2} + z_{0} \frac{σ_{z} (t)}{σ_{z}} \end{aligned}

$\begin{aligned} x(t) &=v_{0 x} t+\sqrt{x_{0}^{2}+y_{0}^{2}} \frac{\sigma_{0}(t)}{\sigma_{0}} \cos \varphi(t) \\ y(t) &=v_{0 y} t+\sqrt{x_{0}^{2}+y_{0}^{2}} \frac{\sigma_{0}(t)}{\sigma_{0}} \sin \varphi(t)\\ z(t) &= v_{0 z} t+\frac{1}{2} g t^{2}+z_{0} \frac{\sigma_{z}(t)}{\sigma_{z}} \end{aligned}$

\begin{aligned} σ_{0}^{2} (t) & = σ_{0}^{2} + {(\frac{ℏ t}{2 m σ_{0}})}^{2} \\ φ (t) & = φ_{0} + \arctan (- \frac{ℏ t}{2 m σ_{0}^{2}}) \\ \cos (φ_{0}) & = \frac{x_{0}}{\sqrt{x_{0}^{2} + y_{0}^{2}}} \\ \sin (φ_{0}) & = \frac{y_{0}}{\sqrt{x_{0}^{2} + y_{0}^{2}}} \\ \sin (\arctan x) & = \frac{x}{\sqrt{1 + x^{2}}} \\ \cos (\arctan x) & = \frac{1}{\sqrt{1 + x^{2}}} \\ \cos (a + b) & = \cos a \cos b - \sin a \sin b \\ \sin (a + b) & = \sin a \cos b + \cos a \sin b \end{aligned}

$\begin{aligned} \sigma_{0}^{2}(t) &= \sigma_{0}^{2}+\left(\frac{\hbar t}{2 m \sigma_{0}}\right)^{2} \\ \varphi(t) &= \varphi_{0}+\arctan \left(-\frac{\hbar t}{2 m \sigma_{0}^{2}}\right) \\ \cos \left(\varphi_{0}\right) &= \frac{x_{0}}{\sqrt{x_{0}^{2}+y_{0}^{2}}} \\ \sin \left(\varphi_{0}\right) &= \frac{y_{0}}{\sqrt{x_{0}^{2}+y_{0}^{2}} } \\ \sin(\arctan x) &= \frac{x}{\sqrt{1+x^2}} \\ \cos(\arctan x) &= \frac{1}{\sqrt{1+x^2}} \\ \cos(a+b) &= \cos a\cos b - \sin a\sin b \\ \sin(a+b) &= \sin a\cos b + \cos a\sin b \end{aligned}$

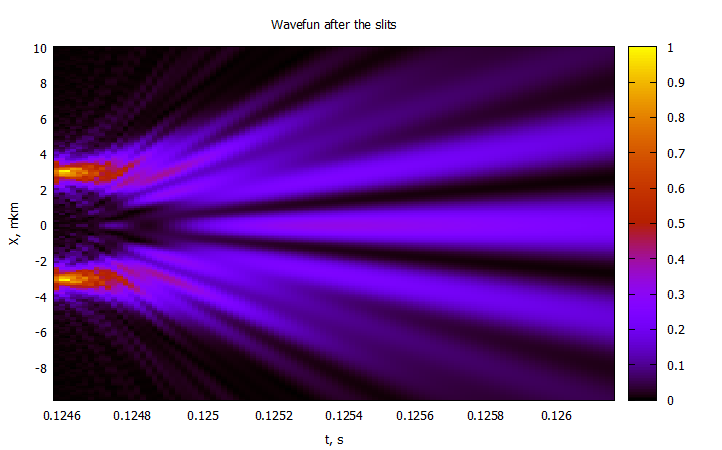
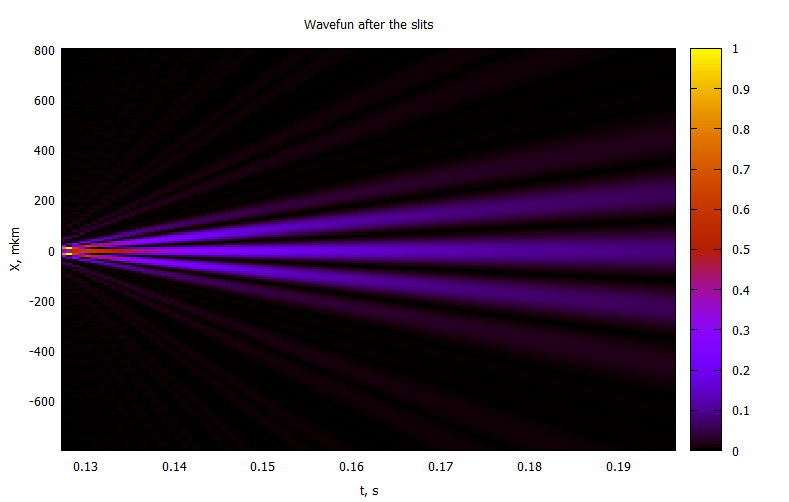
function xbs(t, xo, yo, vo)

    cosϕ = xo / sqrt( xo^2 + yo^2 )
    sinϕ = yo / sqrt( xo^2 + yo^2 )
    atnx = -ħ*t / (2m*σ₀^2)
    sinatnx = atnx / sqrt( atnx^2 + 1)
    cosatnx =    1 / sqrt( atnx^2 + 1)
    cosϕt = cosϕ * cosatnx - sinϕ * sinatnx
    #sinϕt = sinϕ*cosatnx + cosϕ*sinatnx

    σ₀t = sqrt( σ₀^2 + ( ħ*t / (2*m*σ₀) )^2 )

    vo*t + sqrt(xo^2 + yo^2) * σ₀t/σ₀ * cosϕt
end

@gp "set title 'Trajectories before slits'" xlab="t, s" ylab="X, mkm" # "set yrange [-10:10]"

@time for i in 1:80

    x0 = randn()*σ₀
    y0 = randn()*σ₀
    v0 = randn()*σv*1e-4

    prtclᵢ = [ xbs(t,x0,y0,v0) for t in Cron1 ]

    @gp :- Cron1 1000000prtclᵢ "with lines notit lw 2 lc rgb 'black'"
    # slits -4-> -2, 2->4 mkm
end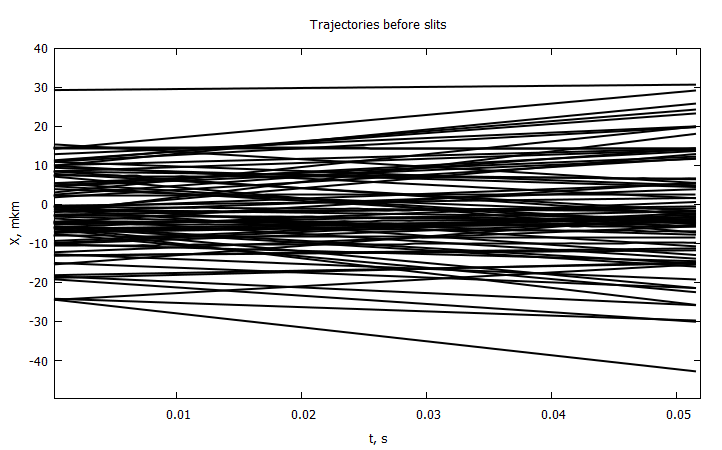

, , , , , . . . , .

Y , , . X . .

" " ,

v_{x} (x, t) = \frac{1}{t - t_{1}} [x + \frac{- 1}{2 (α^{2} + β_{t}^{2})} (β_{t} I m (\frac{C (x, t)}{H (x, t)}) + α Re (\frac{C (x, t)}{H (x, t)}) - β_{t} γ_{x, t})]

$v_{x}(x, t)=\frac{1}{t-t_{1}}\left[x+\frac{-1}{2\left(\alpha^{2}+\beta_{t}^{2}\right)}\left(\beta_{t} I m\left(\frac{C(x, t)}{H(x, t)}\right)+\alpha \operatorname{Re}\left(\frac{C(x, t)}{H(x, t)}\right)-\beta_{t} \gamma_{x, t}\right)\right]$

18+

\begin{aligned} H (x, t) & = \int_{X_{A} - b}^{X_{A} + b} f (x, u, t) d u + \int_{X_{B} - b}^{X_{B} + b} f (x, u, t) d u \\ C (x, t) & = [f (x, u, t)]_{u = X_{A} - b}^{u = X_{A} + b} + [f (x, u, t)]_{u = X_{B} - b}^{u = X_{B} + b} \\ f (x, u, t) & = \exp [(α + i β_{t}) u^{2} + i γ_{x, t} u] \\ α & = - \frac{1}{4 σ_{0}^{2} (1 + {(\frac{ℏ t_{1}}{2 m σ_{0}^{2}})}^{2})} \\ β_{t} & = \frac{m}{2 ℏ} (\frac{1}{t - t_{1}} + \frac{1}{t_{1} (1 + {(\frac{2 m σ_{0}^{2}}{ℏ t_{1}})}^{2})}) \\ γ_{x, t} & = - \frac{m x}{ℏ (t - t_{1})} \end{aligned}

$\begin{aligned} H(x, t) &= \int_{X_{A}-b}^{X_{A}+b} f(x, u, t) d u+\int_{X_{B}-b}^{X_{B}+b} f(x, u, t) d u \\ C(x, t) &= [f(x, u, t)]_{u=X_{A}-b}^{u=X_{A}+b}+[f(x, u, t)]_{u=X_{B}-b}^{u=X_{B}+b} \\ f(x, u, t) &= \exp \left[\left(\alpha+i \beta_{t}\right) u^{2}+i \gamma_{x, t} u\right]\\ \alpha &= -\frac{1}{4 \sigma_{0}^{2}\left(1+\left(\frac{\hbar t_{1}}{2 m \sigma_{0}^{2}}\right)^{2}\right)} \\ \beta_{t} &= \frac{m}{2 \hbar}\left(\frac{1}{t-t_{1}}+\frac{1}{t_{1}\left(1+\left(\frac{2 m \sigma_{0}^{2}}{\hbar t_{1}}\right)^{2}\right)}\right) \\ \gamma_{x, t} &= -\frac{m x}{\hbar\left(t-t_{1}\right)} \end{aligned}$

function Uₓ(t, x)

    γ = -m*x / ( ħ*(t-tf1) )
    β = m/(2ħ) * ( 1/(t-tf1) + 1 / ( tf1*( 1 + (2m*σ₀^2 / (ħ*tf1) )^2 ) ) )
    α = -( 4σ₀^2 * ( 1 + ( ħ*tf1 / (2m*σ₀^2) )^2 ) )^-1

    f(x, u, t) = exp( ( α + im*β )*u^2 + im*γ*u )

    C = f(x, a2, t) - f(x, a1, t) + f(x, b2, t) - f(x, b1, t)
    H = trapez( u-> f(x, u, t) , a1, a2, 400) + trapez( u-> f(x, u, t) , b1, b2, 400)

    return 1/(t-tf1) * ( x - 0.5/(α^2 + β^2) * ( β*imag(C/H) + α*real(C/H) - β*γ ) )
end

init() = bitrand()[1] ? rand()*(b2 - b1) + b1 : rand()*(a2 - a1) + a1
myrng(a, b, N) = collect( range(a, stop = b, length = N ÷ 2) )

n = 1
xx = 0
ξ = 1e-5
while xx < Cron2[end]-Cron2[1]
    n+=1
    xx += (ξ*n)^2 
end
n

steps = [ (ξ*i)^2 for i in 1:n1 ]
Cronadapt = accumulate(+, steps, init = Cron2[1] )

function modelsolver(Np = 10, Nt = 100)

    #xo = [ init() for i = 1:Np ] # 
    xo = vcat( myrng(a2, a1, Np), myrng(b1, b2, Np) ) # 

    xpath = zeros(Nt, Np)
    xpath[1,:] = xo

    for i in 2:Nt, j in 1:Np
        xpath[i,j] = rk4(Uₓ, Cronadapt[i], xpath[i-1,j], steps[i] )
    end

    xpath
end

@time paths = modelsolver(20, n);

@gp "set title 'Trajectories after the slits'" xlab="t, s" ylab="X, mkm" "set yrange [-800:800]"
for i in 1:size(paths, 2)
    @gp :- Cronadapt 1e6paths[:,i] "with lines notit lw 1 lc rgb 'black'"
end

- 4 , . 2

, : , , .

. , ,

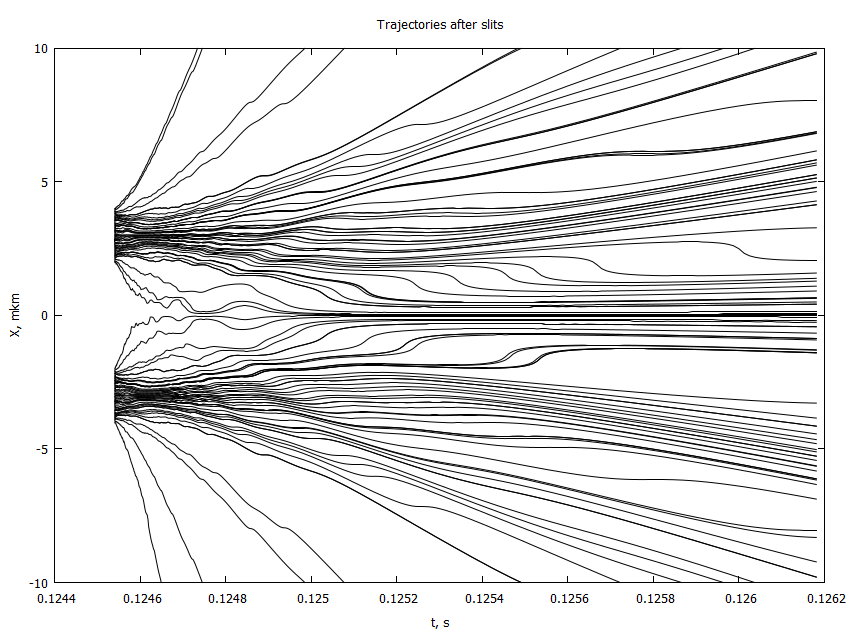
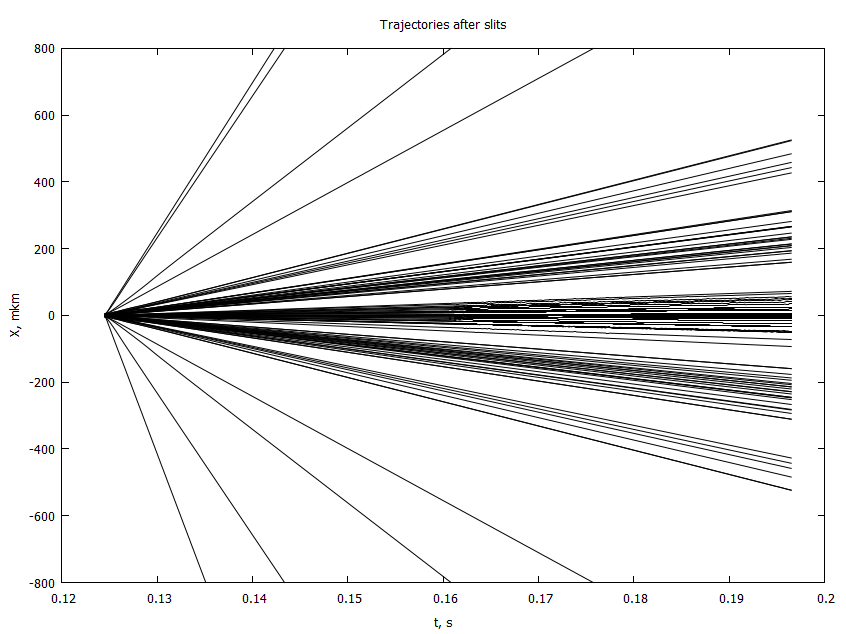
function yas(t, xo, yo, vo)

    cosϕ = xo / sqrt( xo^2 + yo^2 )
    sinϕ = yo / sqrt( xo^2 + yo^2 )
    atnx = -ħ*t / (2m*σ₀^2)
    sinatnx = atnx / sqrt( atnx^2 + 1)
    cosatnx =    1 / sqrt( atnx^2 + 1)
    #cosϕt = cosϕ * cosatnx - sinϕ * sinatnx
    sinϕt = sinϕ*cosatnx + cosϕ*sinatnx

    σ₀t = sqrt( σ₀^2 + ( ħ*t / (2*m*σ₀) )^2 )

    vo*t + sqrt(xo^2 + yo^2) * σ₀t/σ₀ * sinϕt
end

function modelsolver2(Np = 10)

    Nt = length(Cronadapt)
    xo = [ init() for i = 1:Np ]
    #xo = vcat( myrng(a2, a1, Np), myrng(b1, b2, Np) )

    xcoord = copy(xo)
    ycoord = zeros(Np)

    for i in 2:Nt, j in 1:Np
        xcoord[j] = rk4(Uₓ, Cronadapt[i], xcoord[j], steps[i] )
    end

    for (i, x) in enumerate(xo)

        y0 = randn()*yh
        v0 = 0 #randn()*σv*1e-4

        ycoord[i] = yas(Cronadapt[end], x, y0, v0)
    end

    xcoord, ycoord
end

@time X, Y = modelsolver2(100);

@gp "set title 'Impacts on the screen'" xlab="X, mm" ylab="Y, mm"# "set xrange [-1:1]"
@gp :- 1000X 1000Y "with points notit pt 7 ps 0.5 lc rgb 'black'"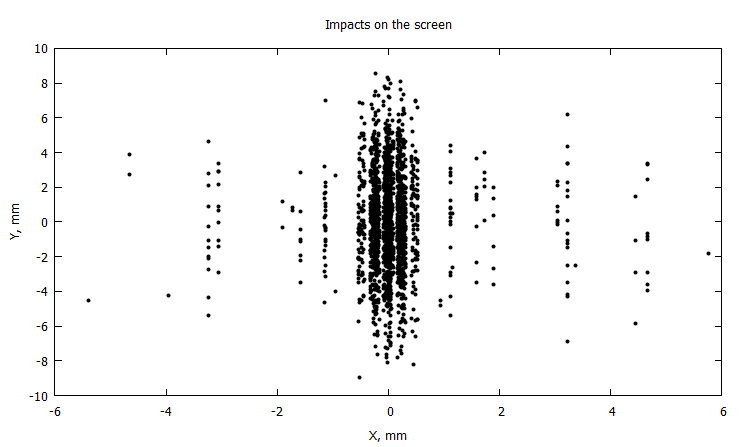

, , . , ,

, , , , , — , .

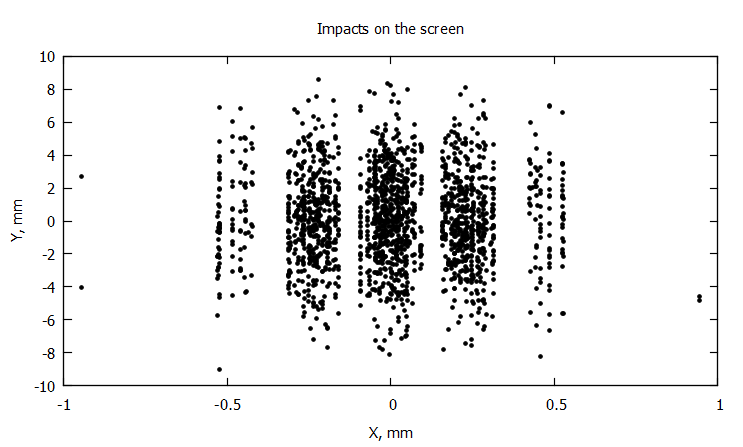
Aplicación obscena

More articles: