1. Introducción
Al realizar estudios de ingeniería y geológicos, puede surgir una tarea relacionada con la comparación de datos de estudios de campo y de laboratorio en los mismos suelos para confirmar el transporte correcto de muestras desde el objeto de estudio al laboratorio (las muestras no se deformaron y / o destruyeron durante el transporte).
Con esta formulación del problema, se puede aplicar la técnica de prueba A / B con los siguientes parámetros:
La métrica medida será el valor promedio de la densidad del esqueleto del suelo (p d , g / cm 3 ), que caracteriza la adición de las muestras. Este valor tiene una ley de distribución normal;
El criterio para probar la hipótesis será la prueba t (prueba de Student): para dos muestras independientes , si los datos comparados de campo (antes del transporte) y de laboratorio (después del transporte) se realizaron en diferentes muestras de suelo; para dos muestras dependientes , si los estudios se realizaron en las mismas muestras.
En el marco de este tema, generaremos dos muestras aleatorias, las cuales compararemos, formularemos hipótesis estadísticas, las contrastaremos y sacaremos conclusiones.
2. Generación de muestras
2.1 Estimación del tamaño de la muestra
Como parte del diseño del experimento, antes de generar las muestras de densidad, estimamos su volumen requerido para un tamaño de efecto dado (ES - tamaño del efecto) , potencia y error de tipo I permisible (α) (las definiciones de estos términos se dan a continuación ). Realizaremos el cálculo utilizando el paquete statsmodels .
El tamaño del efecto (estandarizado) es el valor que caracteriza la diferencia que queremos detectar, igual a la relación entre la diferencia en los valores medios entre las muestras y la desviación estándar ponderada. En nuestro caso:
La desviación estándar ponderada S combinada para muestras del mismo tamaño se puede calcular mediante la fórmula:
(Cohen, 1988) ES = 0.2 - ; 0.5 - ; 0.8 - .
– II ( 80%).
I II :
H0 |
H1 |
|
|---|---|---|
H0 |
H0 |
II (β) |
H0 |
I (α) |
H0 (power = 1-β) |
:
α = 0.05 ( )
ES = 0.5 ( ).
Power = 0.8 ( ).
:
#
import numpy as np
from statsmodels.stats.power import TTestIndPower
from matplotlib.pyplot import figure
import matplotlib.pyplot as plt
import scipy
from statsmodels.stats.weightstats import *
#
effect = 0.5
alpha = 0.05
power = 0.8
analysis = TTestIndPower()
#
size = analysis.solve_power(effect, power=power, alpha=alpha)
print(f' , .: {int(size)}')
, .: 63
, 63 . 65 .
.
plt.figure(figsize=(10, 7), dpi=80)
results = dict((i/10, analysis.solve_power(i/10, power=power, alpha=alpha))
for i in range(2, 16, 1))
plt.plot(list(results.keys()), list(results.values()), 'bo-')
plt.grid()
plt.title(' \n ')
plt.ylabel(' n, .')
plt.xlabel(' ES, ..')
for x,y in zip(list(results.keys()),list(results.values())):
label = "{:.0f}".format(y)
plt.annotate(label,
(x,y),
textcoords="offset points",
xytext=(0,10),
ha='center')
plt.show()
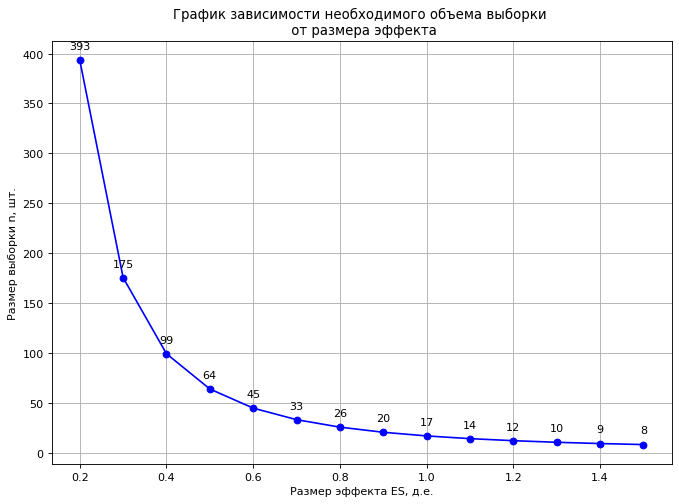
, ES. : 0,03 /3 0,1 /c3 (ES = 0,03 /3 / 0,1 /3 = 0,3 ..), 175 (power=0.80, α=0.05).
2.2
, numpy.
( ) . (X̄) (S):
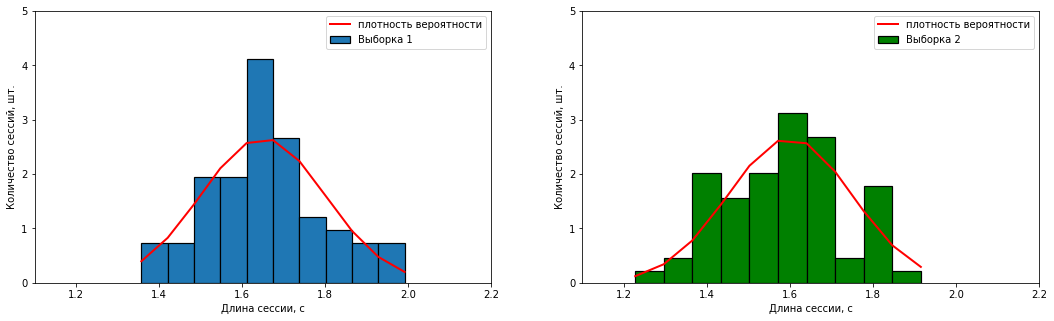
– X̄1= 1,65 /3, S1 = 0.15 /3;
– X̄2 = 1,60 /3, S2 = 0.15 /3.
loc_1 = 1.65
sigma_1 = 0.15
loc_2 = 1.60
sigma_2 = 0.15
sample_size = 65
#
sample_1 = np.random.normal(loc=loc_1, scale=sigma_1, size=sample_size)
sample_2 = np.random.normal(loc=loc_2, scale=sigma_2, size=sample_size)
" " .
fig, axes = plt.subplots(ncols=2, figsize=(18, 5))
max_y = np.max(np.hstack([sample_1,sample_2]))
# 1
count_1, bins_1, ignored_1 = axes[0].hist(sample_1, 10, density=True,
label=" 1", edgecolor='black',
linewidth=1.2)
axes[0].plot(bins_1, 1/(sigma_1 * np.sqrt(2 * np.pi)) *
np.exp( - (bins_1 - loc_1)2 / (2 * sigma_12)),
linewidth=2, color='r', label=' ')
axes[0].legend()
axes[0].set_xlabel(u' , ')
axes[0].set_ylabel(u' , .')
axes[0].set_ylim([0, 5])
axes[0].set_xlim([1.1, 2.2])
# 2
count_2, bins_2, ignored_2 = axes[1].hist(sample_2, 10, density=True,
label=" 2", edgecolor='black',
linewidth=1.2, color="green")
axes[1].plot(bins_2, 1/(sigma_2 * np.sqrt(2 * np.pi)) *
np.exp( - (bins_2 - loc_2)2 / (2 * sigma_22)),
linewidth=2, color='r', label=' ')
axes[1].legend()
axes[1].set_xlabel(u' , ')
axes[1].set_ylabel(u' , .')
axes[1].set_ylim([0, 5])
axes[1].set_xlim([1.1, 2.2])
plt.show()
#
fig, ax = plt.subplots(figsize=(8, 8))
axis = ax.boxplot([sample_1, sample_2], labels=[' 1', ' 2'])
data = np.array([sample_1, sample_2])
means = np.mean(data, axis = 1)
stds = np.std(data, axis = 1)
for i, line in enumerate(axis['medians']):
x, y = line.get_xydata()[1]
text = ' μ={:.2f}\n σ={:.2f}'.format(means[i], stds[i])
ax.annotate(text, xy=(x, y))
plt.ylabel(' , /3')
plt.show()
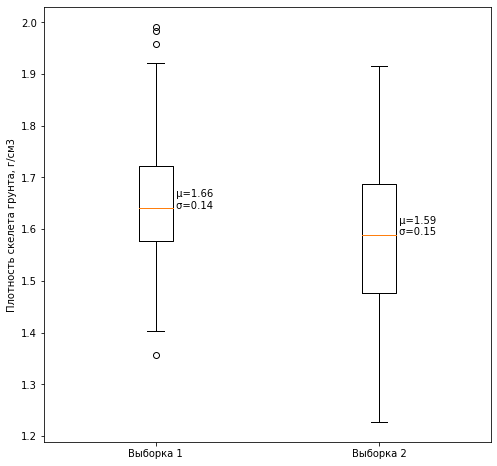
3.
. :
1. , t- ;
2. , t- .
.
1.
.
H0: μ1 = μ2.
H1: μ1≠μ2.
:
: T(X1n1,X2n2)≈~St(ν), ν
ttest_ind stats.
t_st, p_val = scipy.stats.ttest_ind(sample_1, sample_2, equal_var = False)
print(f't- {round(t_st, 2)}')
print(f' t- \
(p-value) {round(p_val, 3)}')
t- 2.92
t- (p-value) 0.004
№ 1
H0 , , 0,05 ( p-value 0.004) .
.
c_m = CompareMeans(DescrStatsW(sample_1), DescrStatsW(sample_2))
print("95%% : \
[%.4f, %.4f]" % c_m.tconfint_diff(usevar='unequal'))
95% : [0.0235, 0.1228]
95% , , 5%.
2.
, ( ) ( ) . , .
H0: μ1 = μ2.
H1: μ1≠μ2.
:
: T(X1n, X2n) ~ St(n-1)
ttest_rel stats.
t_st, p_val = stats.ttest_rel(sample_1, sample_2)
print(f't- {round(t_st, 2)}')
print(f' t- \
(p-value) {round(p_val, 3)}')
t- 2.79
t- (p-value) 0.007
№ 2
H0 , , 0,05 ( p-value 0.007).
Para mayor claridad, estimemos también el intervalo entre las medias de estas muestras.
print("95%% confidence interval: [%.4f, %.4f]"
% DescrStatsW(sample_1 - sample_2).tconfint_mean())
Intervalo de confianza del 95%: [0.0208, 0.1255]
Dado que cero no cae dentro del intervalo de confianza del 95% considerado, podemos concluir que los valores medios de las muestras consideradas difieren.
5. Resultado
En este artículo, examinamos la posibilidad de utilizar el lenguaje Python para resolver un problema práctico en ingeniería geológica, con un estudio de acompañamiento sobre el tema del tamaño de muestra requerido para probar hipótesis.