Vea la publicación anterior aquí .
Regresión
Si bien puede ser útil saber que las dos variables están correlacionadas, no podemos usar esta información por sí sola para predecir el peso de los nadadores olímpicos en presencia de datos de altura, o viceversa. Al establecer la correlación, medimos la fuerza y el signo de la conexión, pero no la pendiente, es decir, Pendiente. Para generar una predicción, necesita conocer la tasa de cambio esperada en una variable para un cambio de unidad dado en otra.
Nos gustaría derivar una ecuación que relacione el valor específico de una variable, la llamada variable independiente, con el valor esperado de otra variable dependiente. Por ejemplo, si nuestra ecuación lineal predice el peso para una altura determinada, el crecimiento es nuestra variable independiente y depende del peso .
Las líneas descritas por estas ecuaciones se denominan líneas de regresión . Este término fue acuñado por el erudito británico del siglo XIX, Sir Francis Galton. Él y su alumno Carl Pearson, quien derivó el coeficiente de correlación, desarrollaron una gran cantidad de métodos para estudiar las relaciones lineales en el siglo XIX, que colectivamente se conocieron como métodos de análisis de regresión.
Recuerde que la correlación no implica causalidad, y los términos "dependiente" e "independiente" no significan causalidad implícita. Son solo nombres para valores matemáticos de entrada y salida. Un ejemplo clásico es la correlación extremadamente positiva entre el número de camiones de bomberos enviados para extinguir un incendio y el daño causado por el incendio. Por supuesto, enviar camiones de bomberos para extinguir un incendio no causa daños en sí mismo. Nadie recomendaría reducir el número de vehículos enviados para extinguir un incendio como una forma de reducir los daños. En tales situaciones, debemos buscar una variable adicional que se relacione causalmente con otras variables y explicar la correlación entre ellas. En este ejemplo, podría ser el tamaño del fuego.... Estas causas subyacentes se denominan variables de confusión porque distorsionan nuestra capacidad para determinar la relación entre las variables dependientes.
Ecuaciones lineales
Las dos variables, que podemos denotar como x y y , pueden ser estrictamente o vagamente relacionados entre sí. La relación más simple entre la variable independiente x y la variable dependiente y es sencilla, que se expresa mediante la siguiente fórmula:
a b . a , b — , . , a = 32 b = 1.8. a b, :
10° x 10:
, , 10° 50°F, . Python pandas, , :
''' '''
celsius_to_fahrenheit = lambda x: 32 + (x * 1.8)
def ex_3_11():
''' '''
df = pd.DataFrame({'C':s, 'F':s.map(celsius_to_fahrenheit)})
df.plot('C', 'F', legend=False, grid=True)
plt.xlabel(' ')
plt.ylabel(' ')
plt.show()
:
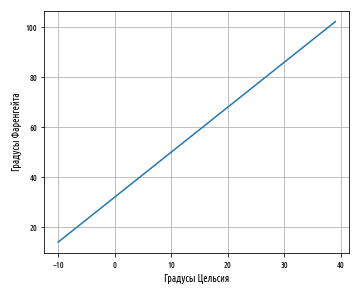
, 0 32 . a — y, x 0.
b; 2. , . , , .
, , . y x. , , , , :
, ε — , , a b x y. y — ŷ, — :
. - , , , . , , , ( ).
a b , x , . , , , x y.
, , , , , . , , .
, , , . , , , .
, , . , . Ordinary Least Squares (OLS), :

, , , . , , , :
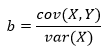
(a) — , X Y:
a b — , .
covariance
, variance
mean
, . :
def slope(xs, ys):
''' ( )'''
return xs.cov(ys) / xs.var()
def intercept(xs, ys):
''' ( Y)'''
return ys.mean() - (xs.mean() * slope(xs, ys))
def ex_3_12():
''' ( )
'''
df = swimmer_data()
X = df[', ']
y = df[''].apply(np.log)
a = intercept(X, y)
b = slope(X, y)
print(': %f, : %f' % (a,b))
: 1.691033, : 0.014296
0.0143 1.6910.
— ( ), () . np.exp
, np.log
. , 5.42 . , , .
, y x. , 1.014 . . , , , .
regression_line
x, ŷ a b.
''' '''
regression_line = lambda a, b: lambda x: a + (b * x) # fn(a,b)(x)
def ex_3_13():
'''
'''
df = swimmer_data()
X = df[', '].apply( jitter(0.5) )
y = df[''].apply(np.log)
a, b = intercept(X, y), slope(X, y)
ax = pd.DataFrame(np.array([X, y]).T).plot.scatter(0, 1, s=7)
s = pd.Series(range(150,210))
df = pd.DataFrame( {0:s, 1:s.map(regression_line(a, b))} )
df.plot(0, 1, legend=False, grid=True, ax=ax)
plt.xlabel(', .')
plt.ylabel(' ')
plt.show()
regression_line
x, a + bx.
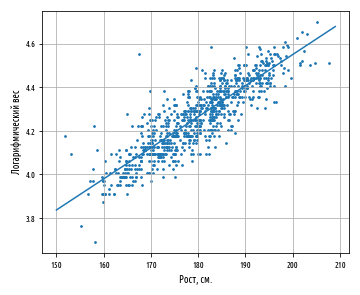
, , ŷ y.
def residuals(a, b, xs, ys):
''' '''
estimate = regression_line(a, b) #
return pd.Series( map(lambda x, y: y - estimate(x), xs, ys) )
constantly = lambda x: 0
def ex_3_14():
''' '''
df = swimmer_data()
X = df[', '].apply( jitter(0.5) )
y = df[''].apply(np.log)
a, b = intercept(X, y), slope(X, y)
y = residuals(a, b, X, y)
ax = pd.DataFrame(np.array([X, y]).T).plot.scatter(0, 1, s=12)
s = pd.Series(range(150,210))
df = pd.DataFrame( {0:s, 1:s.map(constantly)} )
df.plot(0, 1, legend=False, grid=True, ax=ax)
plt.xlabel(', .')
plt.ylabel('')
plt.show()
— , Y X. , :
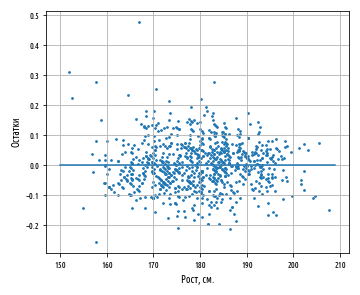
, , -, , . , . , , .
, , , . , . , , . , .
, . . , , , .. . , , , .
. , , , , .
R-
, , .. , . R2, R-, 0 1 . .
, R2 1, Y X. R2 :
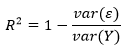
var(ε) — var(Y) — Y. , - . , . var(Y), .. .
, , a + bx. .
var(ε)/var(Y) — , . . , . R2 — , .
r, R2 , . , .
R2 . — , R2. R2 .
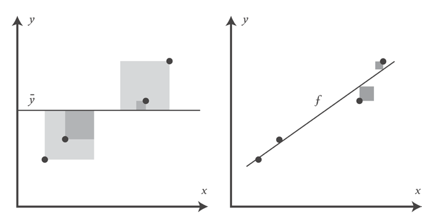
, , , , f. , y. R2 y:
def r_squared(a, b, xs, ys):
''' (R-)'''
r_var = residuals(a, b, xs, ys).var()
y_var = ys.var()
return 1 - (r_var / y_var)
def ex_3_15():
''' R-
'''
df = swimmer_data()
X = df[', '].apply( jitter(0.5) )
y = df[''].apply(np.log)
a, b = intercept(X, y), slope(X, y)
return r_squared(a, b, X, y)
0.75268223613272323
0.753. , 75% , 2012 ., .
( ), R2 r :
r , Y X, R2 0.52, .. 0.25.
, . , . .
. , , β (), :
- , β1 = a β2 = b , x1 1, β1 — , , x1 () , .
β, , :
x1 xn , y. β1 βn , .
, : , , , . , , .
, x. pandas, , : .
Los ejemplos de código fuente para esta publicación están en mi repositorio de Github. Todos los datos de origen se toman del repositorio del autor del libro.
El tema de la próxima publicación, la publicación # 3 , será las operaciones matriciales, la ecuación normal y la colinealidad.