Cuanto más conozco a la gente, más me gusta mi perro.
-Mark Twain
En la serie anterior de publicaciones para principiantes del libro de remezclas Henry Garner « Investigación de datos de Clojure » (Clojure para ciencia de datos) en Python, hemos revisado métodos para describir la muestra en términos de estadísticas de resumen y los métodos de inferencia estadística son parámetros de población. Este análisis nos dice algo sobre la población en general y sobre la muestra en particular, pero no nos permite hacer afirmaciones muy precisas sobre sus elementos individuales. Esto se debe a que al reducir los datos a solo dos estadísticas, la media y la desviación estándar, se pierde una gran cantidad de información.
A menudo necesitamos ir más allá y establecer una relación entre dos o más variables, o predecir una variable en presencia de otra. Y eso nos lleva al tema de esta serie de 5 publicaciones: explorar la correlación y la regresión. La correlación se ocupa de la fuerza y la direccionalidad de una relación entre dos o más variables. La regresión determina la naturaleza de esta relación y permite realizar predicciones a partir de ella.
Esta serie de publicaciones cubrirá la regresión lineal . Dada una muestra de datos, nuestro modelo aprenderá una ecuación lineal que le permitirá hacer predicciones sobre datos nuevos que nunca antes se habían visto. Para hacer esto, regresaremos a la biblioteca de pandas y examinaremos la relación entre la altura y el peso en los atletas olímpicos. Introduciremos el concepto de matrices y le mostraremos cómo administrarlas usando la biblioteca de pandas.
Acerca de los datos
, Guardian News and Media Ltd., , 2012 . . .
, , , .
all-london-2012-athletes.tsv . pandas, «Python, », read_csv
:
def load_data():
return pd.read_csv('data/ch03/all-london-2012-athletes-ru.tsv', '\t')
def ex_3_1():
'''
2012 .'''
return load_data()
Python Jupyter, :
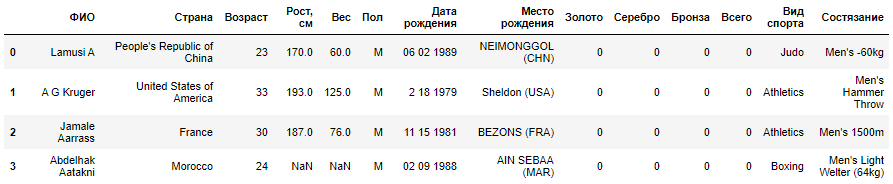
|
|
|
|
( , ) :
,
,
, .
, .
«» «»
( )
,
,
,
, , , . , .
2012 . . , , :
def ex_3_2():
'''
'''
df = load_data()
df[', '].hist(bins=20)
plt.xlabel(', .')
plt.ylabel('')
plt.show()
:
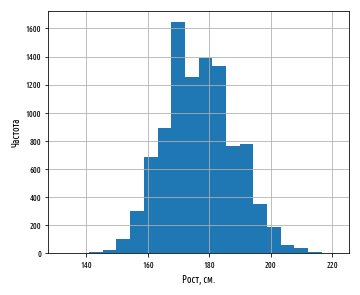
, . 177 . :
def ex_3_3():
''' '''
df = load_data()
df[''].hist(bins=20)
plt.xlabel('')
plt.ylabel('')
plt.show()
:
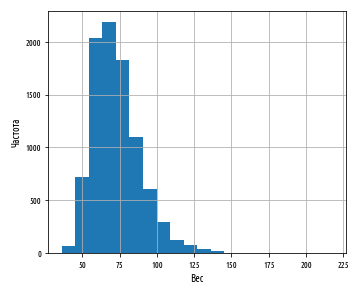
. , , , - . pandas skew
:
def ex_3_4():
''' '''
df = load_data()
swimmers = df[ df[' '] == 'Swimming']
return swimmers[''].skew()
0.23441459903001483
, numpy np.log
:
def ex_3_5():
'''
'''
df = load_data()
df[''].apply(np.log).hist(bins=20)
plt.xlabel(' ')
plt.ylabel('')
plt.show()
:
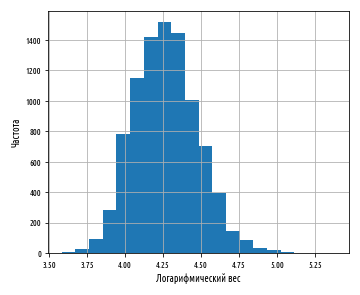
. , .
— , . . , .
, () . , , . 10 e, , 2.718. numpy np.log
np.exp
e. loge , ln, - , .
, . , c 1931 . , , . , , .
, , , , , .
, , , Wolfram MathWorld, .
, . , , .
, . , , :
def swimmer_data():
''' '''
df = load_data()
return df[df[' '] == 'Swimming'].dropna()
def ex_3_6():
''' '''
df = swimmer_data()
xs = df[', ']
ys = df[''].apply( np.log )
pd.DataFrame(np.array([xs,ys]).T).plot.scatter(0, 1, s=12, grid=True)
plt.xlabel(', .')
plt.ylabel(' ')
plt.show()
:

, . , . :

, , , . , , , . , , , - ( . . ). , , , , . ( ) , , , , , . .
, , 180 , 179.5 180.5 , 80 79.5 80.5 . , -0.5 0.5 (, c , ):
def jitter(limit):
''' ( )'''
return lambda x: random.uniform(-limit, limit) + x
def ex_3_7():
''' '''
df = swimmer_data()
xs = df[', '].apply(jitter(0.5))
ys = df[''].apply(jitter(0.5)).apply(np.log)
pd.DataFrame(np.array([xs,ys]).T).plot.scatter(0, 1, s=12, grid=True)
plt.xlabel(', .')
plt.ylabel(' ')
plt.show()
:

, — , , , .
. .
, X Y, :
xi — X i, yi — Y i, x̅ — X, y̅ — Y. X Y , : , — , , . , , , , . .
:

Python :
def covariance(xs, ys):
''' (, .. n-1)'''
dx = xs - xs.mean()
dy = ys - ys.mean()
return (dx * dy).sum() / (dx.count() - 1)
, pandas cov
:
df[', '].cov(df[''])
1.3559273321696459
1.356, . .
. , . -1 +1. .
, . standard score, z- — , . , , — . , .
r , dxi dyi :

X Y , , σx σy — X Y:

, , r.
. :
def variance(xs):
''' ,
n <= 30'''
x_hat = xs.mean()
n = xs.count()
n = n - 1 if n in range( 1, 30 ) else n
return sum((xs - x_hat) ** 2) / n
def standard_deviation(xs):
''' '''
return np.sqrt(variance(xs))
def correlation(xs, ys):
''' '''
return covariance(xs, ys) / (standard_deviation(xs) *
standard_deviation(ys))
pandas corr
:
df[', '].corr(df[''])
, r . r -1.0 1.0, .
, r = 0, , . . , , r :

, , y = 0. r 0, . ; y . .
:
def ex_3_8():
''' pandas
'''
df = swimmer_data()
return df[', '].corr( df[''].apply(np.log))
0.86748249283924894
0.867, , , .
r ρ
, . ; , : . r, ρ ().
, , , , . , . , , , -.
— , , — . , r, ρ, :
r
, , , . , , , . , .
, , (, , ) . , , .
, , :
H0 - , . , , .
H1 - , . , , . , .
r :

, r (, ρ ), , , .
t- t-:

df — . n - 2, n — . , :

t- 102.21. p- t-. scipy () t- stats.t.cdf
, (1-cdf) stats.t.sf
. p- . 2, :
def t_statistic(xs, ys):
''' t-'''
r = xs.corr(ys) # , correlation(xs, ys)
df = xs.count() - 2
return r * np.sqrt(df / 1 - r ** 2)
def ex_3_9():
''' t-'''
df = swimmer_data()
xs = df[', ']
ys = df[''].apply(np.log)
t_value = t_statistic(xs, ys)
df = xs.count() - 2
p = 2 * stats.t.sf(t_value, df) #
return {'t-':t_value, 'p-':p}
{'p-': 1.8980236317815443e-106, 't-': 25.384018200627057}
P- , 0, , , , . .
, , , , , , , , , ρ, . , r ( %), ρ .
, . r 1, r r .

r- ρ, 0.6.
, z- r . , , .
z- :

z :

, r z z-, SEz r.
SEz, , . 1.96, , 95% . , 1.96 r ρ 95%- .

, scipy stats.norm.ppf
. , .
, , , .. 2.5%, , 95%- . 100%. , 95% , 97.5%:
def critical_value(confidence, ntails): #
'''
'''
lookup = 1 - ((1 - confidence) / ntails)
return stats.norm.ppf(lookup, 0, 1) # mu=0, sigma=1
critical_value(0.95, 2)
1.959963984540054
95%- z- ρ :

zr SEz, :

r=0.867 n=859 1.137 1.722. z- r-, z-:

:
def z_to_r(z):
''' z- r-'''
return (np.exp(z*2) - 1) / (np.exp(z*2) + 1)
def r_confidence_interval(crit, xs, ys):
'''
'''
r = xs.corr(ys)
n = xs.count()
zr = 0.5 * np.log((1 + r) / (1 - r))
sez = 1 / np.sqrt(n - 3)
return (z_to_r(zr - (crit * sez))), (z_to_r(zr + (crit * sez)))
def ex_3_10():
'''
'''
df = swimmer_data()
X = df[', ']
y = df[''].apply(np.log)
interval = r_confidence_interval(1.96, X, y)
print(' (95%):', interval)
(95%): (0.8499088588880347, 0.8831284878884087)
95%- ρ, 0.850 0.883. , .
Los ejemplos de código fuente para esta publicación están en mi repositorio de Github. Todos los datos de origen se toman del repositorio del autor del libro.
En la próxima publicación, la publicación n. ° 2 , se considerará el tema de la serie en sí: regresión y técnicas para evaluar su calidad.