😍 🚵🏼 👨🏻‍🚀 Matrix-Rematrix 🎅🏻 ⭕️ 🤞🏼

El trabajo de una red neuronal se basa en la manipulación de matrices. Para el entrenamiento, se utilizan una variedad de métodos, muchos de los cuales han surgido del método de descenso de gradientes, donde es necesario poder manejar matrices, calcular gradientes (derivadas con respecto a matrices). Si miras debajo del capó de una red neuronal, puedes ver cadenas de matrices, que a menudo parecen intimidantes. En pocas palabras, "la matriz nos espera a todos". Es hora de conocerse mejor.

Para ello, seguiremos los siguientes pasos:

Consideremos manipulaciones con matrices: transposición, multiplicación, gradiente;
;
.

NumPy . , , , , . , , , - , , , . , - : , .

-

- , , , . , , , Google TensorFlow.

, , , , , $a_ {i}$ , i = 0, 1, 2, ..., n-1 ; norte - .

import numpy as np #   numpy
a=np.array([1,2,5])
a.ndim #  ,   = 1
a.shape #      (3,)
a.shape[0] #      = 3

$a_ {i} \ cdot b_ {i} = a_ {0} \ cdot b_ {0} + a_ {1} \ cdot b_ {1} + a_ {2} \ cdot b_ {2}$ . , , 0 2 .

b=np.array([3,4,7])
np.dot(a,b) #   = 46
a*b #   array([ 3,  8, 35])
np.sum(a*b) # = 46

( ) - , $A_ {i, j}$ . , $A_ {0, 2}$ - 0- 2- . , .

A=np.array([[ 1,  2,  3],
            [ 2,  4,  6]])
A # array([[1, 2, 3],
  #        [2, 4, 6]])
A[0, 2] #    ,    = 3
A.shape # (2, 3)   2 , 3

C = AB , $C_ {i, k} = A_ {i, j} B_ {j, k}$ . , ( )

B=np.array([[7, 8, 1, 3],
            [5, 4, 2, 7],
            [3, 6, 9, 4]])
A.shape[1] == B.shape[0] # true
A.shape[1], B.shape[0] # (3, 3) 
A.shape, B.shape # ((2, 3), (3, 4))
C = np.dot(A, B)
C # array([[26, 34, 32, 29],
  #        [52, 68, 64, 58]]); 
  #  , C[0,1]=A[0,0]B[0,1]+ A[0,1]B[1,1]+A[0,2]B[2,1]=1*8+2*4+3*6=34
C.shape # (2, 4)

licenciado en Letras , :

np.dot(B, A) # ValueError: shapes (3,4) and (2,3) not aligned: 4 (dim 1) != 2 (dim 0)

, .

, . , $a_ {i, 0}$ $b_ {j, 0}$ . $D_ {i, j} = a_ {i, 0} b_ {j, 0}$ . , , , $b_ {j, 0} = (bT) _ {0, j}$ , - ( NumPy). $D = a \ cdot bT$ . , $DT = (a \ cdot bT) .T = (bTT) \ cdot aT = b \ cdot aT$ .

a = np.reshape(a, (3,1)) #   ,  a.shape = (3,)  (3,1),
b = np.reshape(b, (3,1)) #  ,  
D = np.dot(a,b.T)
D # array([[ 3,  4,  7],
  #        [ 6,  8, 14],
  #        [15, 20, 35]])

, . , .

, , . (cost function). , . . , (learning rate), , (epoch). , . (), . . , , , .

, ( , ).

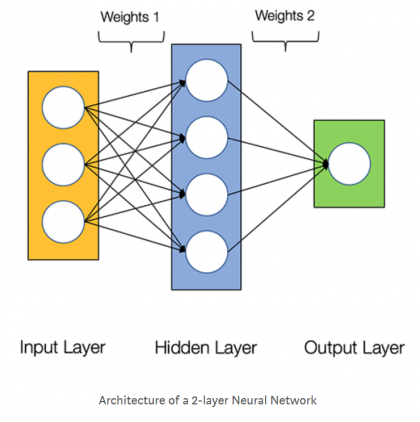
- (samples) . . , (), ( ) - (samples), - (features).

, ( ). (, …) , , . , .

!

, , . , “ ” . , , . , , . , , , .

, 10 . , (10, 3). “ ”, . , . , :

, , 0 50 ;

X=np.random.randint(0, 50, (10, 3))

0 1;

X=np.random.rand(10, 3)

$\ mu = 2$ $\ sigma ^ 2 = 16$ . , , $N (\ mu, \ sigma ^ 2)$ ;

X=4*np.random.randn(10, 3) + 2

$\ mu = 0$ $\ sigma = 1$ , .

, (10, 3) $W ^ {(1)}$ , . , , . , , , $W ^ {(1)}$ (3, 4) . , $(10, 3) (3, 4) \ Flecha derecha (10, 4)$ . , $X \ cdot W ^ {(1)}$ (10,4) , - - , . . , (m, n) ( metro , norte ) $a_ {i, j}$ , f (A) , $f (a_ {i, j})$ ; , , $a_ {1,2} \ Flecha derecha f (a_ {1,2})$ , . , $W ^ {(2)}$ , (4, 1) . , $(10, 3) (3, 4) (4, 1) \ Flecha derecha (10, 1)$ . , $\hat{Y}$ 10- (samples) . :

$\hat{Y}=X\cdot W^{(1)}\cdot W^{(2)}, \quad\quad \hat{Y}_{i,0}=X_{i,j} W_{j,k}^{(1)} W_{k,0}^{(2)}.$

, . (bias).

. : , , , .

X=np.random.randint(0, 50, (10, 3))
w1=2*np.random.rand(3,4)-1 #       -1  +1
w2=2*np.random.rand(4,1)-1
Y=np.dot(np.dot(x,w1),w2) #   
Y.shape # (10, 1)
Y.T.shape # (1, 10)
(np.dot(Y.T,Y)).shape # (1, 1), ,

. -1 +1, “” ( ).

. f_1 “ ”, - .

$\hat{Y}_{i,0}=f_2(f_1(X_{i,j} W_{j,k}^{(1)})W_{k,0}^{(2)}),$ $\hat{Y}=f_2(f_1(X \cdot W^{(1)})\cdot W^{(2)}).$

, .

$\triangle=\sum_i(Y_{i,0}-\hat{Y}_{i,0})^2=\sum_i\widetilde{Y}_{i,0}^2=(\widetilde{Y}.T)_{0,i}\widetilde{Y}_{i,0}=(\widetilde{Y}.T)\cdot\widetilde{Y},$

(X,Y) - , $\widetilde{Y}_{i,0}=Y_{i,0}-\hat{Y}_{i,0}$ . , $(\widetilde{Y}.T)_{0,i}=\widetilde{Y}_{i,0}$ .

, . .

. - . , . , .

- , . f(x) $f^{'}(x_0)=0$ , “ ” - . , , . , , . : - , , - . (, 16 ), , . . , $f^{'}(W)<0$ , , , $f^{'}(W)>0$ , . , .

$W\Rightarrow W+\mu\cdot\delta W=W-\mu\cdot\frac{\partial \triangle}{\partial W},$

$W_{i,j}\Rightarrow W_{i,j}+\mu\cdot\delta W_{i,j}=W_{i,j}-\mu\cdot\frac{\partial \triangle}{\partial W_{i,j}},$

$\mu$ - (learning rate). , . . - , , . , - .

.

$\frac{\partial a_{m, n}}{\partial a_{i,j}}=\delta_{m,i}\delta_{n,j},$

$\delta_{i,j}$ - , , i=j . , $\delta_{1,1}=1$ , $\delta_{2,1}=0$ . : .

$\frac{\partial \triangle}{\partial W_{m,n}}=-2\sum_i(Y_{i,0}-\hat{Y}_{i,0})\frac{\partial \hat{Y}_{i,0}}{\partial W_{m,n}}=-2\widetilde{Y}_{i,0}\frac{\partial \hat{Y}_{i,0}}{\partial W_{m,n}},$

, , $\widetilde{Y}_{i,0}=Y_{i,0}-\hat{Y}_{i,0}$ , .

. . , , .

, $\hat{Y}_{i,0}=X_{i,j} W_{j,k}^{(1)} W_{k,0}^{(2)}$ ,

$\frac{\partial \triangle}{\partial W_{m,0}^{(2)}}=-2\widetilde{Y}_{i,0}\frac{\partial \hat{Y}_{i,0}}{\partial W_{m,0}^{(2)}}=-2\widetilde{Y}_{i,0}X_{i,j} W_{j,k}^{(1)}\delta_{k,m}=-2\widetilde{Y}_{i,0}X_{i,j} W_{j,m}^{(1)}=-2\widetilde{Y}_{i,0}(X\cdot W^{(1)})_{i,m}$

, $A_{i,m}=(A.T)_{m.i}$ . , :

$\delta W_{m,0}^{(2)}=-\frac{\partial \triangle}{\partial W_{m,0}^{(2)}}=2((X\cdot W^{(1)}).T)_{m,i}\widetilde{Y}_{i,0},$

$\delta W^{(2)}=2((X\cdot W^{(1)}).T)\cdot \widetilde{Y}.$

, , , $\delta W^{(2)}$ . $X\cdot W^{(1)}$ (10,3)(3,4)=(10,4) , - (4,10) . $\widetilde{Y}$ $\hat{Y}$ - (10,1) . , $\delta W^{(2)}$ (4,10)(10,1)=(4,1) , .

deltaW2=2*np.dot(np.dot(X,w1).T,Y)
deltaW2.shape # (4,1)

$W^{(1)}$ .

$\frac{\partial \triangle}{\partial W_{m,n}^{(1)}}=-2\widetilde{Y}_{i,0}\frac{\partial \hat{Y}_{i,0}}{\partial W_{m,n}^{(1)}}=-2\widetilde{Y}_{i,0}X_{i,j} \delta_{j,m}\delta_{k,n}W_{k,0}^{(2)}=-2\widetilde{Y}_{i,0}X_{i,m} W_{n,0}^{(2)}=-2(X.T)_{m,i}\widetilde{Y}_{i,0}(W^{(2)}.T)_{0,n},$ $\delta W^{(1)}=2(X.T)\cdot \widetilde{Y}\cdot (W^{(2)}.T).$

, “ ”, “ ” - . , , . : “” ( ), , .

$\delta W^{(1)}$ : (3,10)(10,1)(1,4)=(3,4) .

. ,, , , . . , . , . , , : z=f(y(x)) , $z_x^{'}=f_y^{'}y_x^{'}$ .

$\hat{Y}_{i,0}=f_2(f_1(X_{i,j} W_{j,k}^{(1)})W_{k,0}^{(2)})\quad\Rightarrow\quad \hat{Y}_{i,0}=f_2(C_{i,0}),$

$C_{i,0}=B_{i,k}W_{k,0}^{(2)}, \quad\quad B_{i,k}=f_1(A_{i,k}), \quad\quad A_{i,k}=X_{i,j} W_{j,k}^{(1)}.$

W_2 , . ,

$\delta W_{m,0}^{(2)}=2\widetilde{Y}_{i,0}\frac{\partial \hat{Y}_{i,0}}{\partial W_{m,0}^{(2)}}=2\widetilde{Y}_{i,0}\frac{\partial f_2(C_{i,0})}{\partial C_{\mu,0}}\frac{\partial C_{\mu,0}}{\partial W_{m,0}^{(2)}}=2\widetilde{Y}_{i,0}f_2^{'}(C_{i,0})\delta_{i,\mu}B_{\mu,k}\delta_{k,m}=2\widetilde{Y}_{i,0}f_2^{'}(C_{i,0})B_{i,m}.$

$\frac{\partial f_2(C_{i,0})}{\partial C_{\mu,0}}=f_2^{'}(C_{i,0})\delta_{i,\mu}, \quad\quad \frac{\partial C_{\mu,0}}{\partial W_{m,0}^{(2)}}=B_{\mu,k}\frac{\partial W_{k,0}^{(2)}}{\partial W_{m,0}^{(2)}}=B_{\mu,k}\delta_{k,m}.$

, - . : $B_{i,m}=(B.T)_{m,i}$ , $f_1(A_{i,m})=(f_1(A).T)_{m,i}$ . ,

$\delta W_{m,0}^{(2)}=2(B.T)_{m,i}\widetilde{Y}_{i,0}f_2^{'}(C_{i,0}) \Rightarrow \delta W^{(2)}=2(B.T)\cdot(\widetilde{Y}*f_2^{'}(C))$

“*” . , , , a*b , ; , $a_{1,2}b_{1,2}$ .

. f_1(x)=x^2 f_2(x)=x^3 . , , . NumPy .

def f1(x): #  
    return np.power(x,2)
def graf1(x): # 
    return 2*x
def f2(x): #  
    return np.power(x,3)
def gradf2(x): # 
    return 3*np.power(x,2)

A=np.dot(X,w1) #   
B=f1(A)        #   
C=np.dot(B,w2) #    
Y=f2() #   
deltaW2=2*np.dot(B.T, Y*gradf2(C))
deltaW2.shape # (4,1)

$W^{(1)}$ , . - .

$\delta W_{m,n}^{(1)}=2\widetilde{Y}_{i,0}\frac{\partial \hat{Y}_{i,0}}{\partial W_{m,n}^{(1)}}=2\widetilde{Y}_{i,0}\frac{\partial f_2(C_{i,0})}{\partial C_{\mu,\nu}}\frac{\partial C_{\mu,\nu}}{\partial B_{l,s}}\frac{\partial B_{l,s}}{\partial W_{m,n}^{(1)}},$

$C_{\mu,\nu}=B_{\mu,k}W_{k,\nu}^{(2)}$ . :

$\frac{\partial f_2(C_{i,0})}{\partial C_{\mu,\nu}}=f_2^{'}(C_{i,0})\delta_{i,\mu}\delta_{0,\nu},\quad\quad \frac{\partial C_{\mu,\nu}}{\partial B_{l,s}}=\delta_{\mu,l}\delta_{k,s}W_{k,\nu}^{(2)},\quad\quad$ $\frac{\partial B_{l,s}}{\partial W_{m,n}^{(1)}}=\frac{\partial B_{l,s}}{\partial A_{r,e}}\frac{\partial A_{r,e}}{\partial W_{m,n}^{(1)}}=f_1^{'}(A_{l,s})\delta_{l,r}\delta_{s,e}\delta_{j,m}\delta_{e,n}X_{r,j}=f_1^{'}(A_{l,s})\delta_{l,r}\delta_{s,n}X_{r,m}.$

$\ delta W_ {m, n} ^ {(1)} = 2 \ widetilde {Y} _ {i, 0} f_2 ^ {'} (C_ {i, 0}) \ delta_ {i, \ mu} \ delta_ {0, \ nu} \ delta _ {\ mu, l} \ delta_ {k, s} W_ {k, \ nu} ^ {(2)} f_1 ^ {'} (A_ {l, s}) \ delta_ {s, n} \ delta_ {l, r} X_ {r, m} = 2 \ widetilde {Y} _ {i, 0} f_2 ^ {'} (C_ {i, 0}) W_ {n, 0} ^ {(2)} f_1 ^ {'} (A_ {i, n}) X_ {i, m},$

$\ delta_ {i, \ mu} \ delta_ {0, \ nu} \ delta _ {\ mu, l} \ delta_ {k, s} \ delta_ {s, n} \ delta_ {l, r} = \ delta_ { i, l} \ delta_ {i, r} \ delta_ {k, n} \ delta_ {s, n}.$

, $\ delta_ {0, \ nu} W_ {k, \ nu} ^ {(2)} = W_ {k, 0} ^ {(2)}$ , metro norte , “”, l, r, k, s .

“” ,

$\ delta W_ {m, n} ^ {(1)} = 2 (XT) _ {m, i} \ widetilde {Y} _ {i, 0} f_2 ^ {'} (C_ {i, 0}) ( W ^ {(2)}. T) _ {0, n} f_1 ^ {'} (A_ {i, n}),$ $\ delta W ^ {(1)} = 2 (XT) \ cdot [[(\ widetilde {Y} * f_2 ^ {'} (C)) \ cdot (W ^ {(2)}. T)] * f_1 ^ {'} (A)].$

, $D_ {i, o} = \ widetilde {Y} _ {i, 0} f_2 ^ {'} (C_ {i, 0}) \ Rightarrow \ widetilde {Y} * f_2 ^ {'} (C)$ , $F_ {i, n} = D_ {io} (W ^ {(2)}. T) _ {0, n}$ , $F_ {i, n} f_1 ^ {'} (A_ {i, n}) \ Flecha derecha F * f_1 ^ {'} (A)$ .

deltaW1=2*np.dot(X.T, np.dot(Y*gradf2(C),w2.T)*gradf1(A))
deltaW1.shape # (3,4)

. .

“, - . -!” ? , , , . , . - , , . ! , , - . , , .

, . James Loy - , , , , , . . , , , . “-”, , , . , TensorFlow Keras. , la fuente original (hay una traducción al ruso).

Escribe códigos, profundiza en fórmulas, lee libros, hazte preguntas.

En cuanto a las herramientas, son Jupyter Notebook ( ¡reglas de Anaconda !), Colab ...

Matrix-Rematrix

-

!

.

More articles: