Este artículo se centrará en conceptos de la teoría de números como la raíz digital y el cuadrado védico.
Este artículo no dice nada sobre la numerología, excepto que es un concepto pseudocientífico.
El propósito de este artículo: mostrar los patrones matemáticos en torno al cálculo de la raíz digital y su relación con los números cíclicos.
Introducción
Hace unos días decidí escribir un artículo sencillo sobre la suma numerológica. Mi objetivo era mostrar que incluso una operación tan simple puede tener una gran cantidad de patrones interesantes. Encontré muchos de estos patrones en la escuela, cuando me aburría en las lecciones de geografía. Tras una inspección más cercana, encontré más patrones de los que esperaba, y esto me llevó de nuevo a mi tema principal favorito de repetición completa .
Después de eso, estudié cuidadosamente lo que encontré, aprendí que muchos de estos conceptos ya existen y decidí reescribir el artículo nuevamente para confiar en conceptos bien conocidos. Además de los conceptos familiares, he agregado mis propias visualizaciones para que la lectura sea un poco más divertida.
Suma de dígitos y raíz digital
La raíz digital de un número natural en un sistema numérico dado es el valor obtenido al calcular iterativamente la suma de dígitos , donde en la primera iteración, se calcula la suma de los dígitos de un número natural, y en cada iteración siguiente, la suma de los dígitos del resultado de la iteración anterior se calcula. La operación se realiza hasta que el valor calculado sea menor que el sistema numérico especificado, es decir hasta que sea igual a un solo dígito.
La fuerza aditiva de un número natural es el número de iteraciones en las que es necesario aplicar la operación de la suma de dígitos para obtener la raíz digital.
Ejemplo: la suma digital de 142857 es 1 + 4 + 2 + 8 + 5 + 7 = 27
La suma digital de 27 es 2 + 7 = 9
Como resultado, la raíz digital del número 142857 = 9, la durabilidad aditiva 142857 = 2.
Python:
def digitalRootRecurrent(number, base):
digitSum = 0
while number > 0:
digitSum += number % base
number //= base
if digitSum >= base:
digitSum = digitalRootRecurrent(digitSum, base)
return digitSum
. , , 50 , , ; , , , .
. , . , , .
: , - 1, - 1.
:
def digitalRoot(number, base):
if number == 0:
return 0
dR = number % (base - 1)
if dR == 0:
dR = base - 1
return dR
, , :

:
firstTermRangeStart = 2
firstTermRangeEnd = 8
secondTermRangeStart = 1
secondTermRangeEnd = 9
base = 10
for j in range(firstTermRangeStart, firstTermRangeEnd + 1):
print()
for i in range(secondTermRangeStart, secondTermRangeEnd + 1):
if i % (secondTermRangeEnd + 1) == 0:
print()
print('dr(',j,'+', i, ') =', digitalRoot(j + i, base), ' ', end='')
, :
, .
: 455 - 123 = 332.
, 4 - 6 8, , :
, :

:
firstTermRangeStart = 1
firstTermRangeEnd = 8
secondTermRangeStart = 1
secondTermRangeEnd = 9
base = 10
for i in range(secondTermRangeStart, secondTermRangeEnd + 1):
print()
for j in range(firstTermRangeStart, firstTermRangeEnd + 1):
print('dr(',j,'*', i, ') =', digitalRoot(i * j, base), ' ', end='')
:
1) [1, 2, 3, 4, 5, 6, 7, 8, 9]
2) [2, 4, 6, 8, 1, 3, 5, 7, 9]
3) [3, 6, 9, 3, 6, 9, 3, 6, 9]
4) [4, 8, 3, 7, 2, 6, 1, 5, 9]
5) [5, 1, 6, 2, 7, 3, 8, 4, 9]
6) [6, 3, 9, 6, 3, 9, 6, 3, 9]
7) [7, 5, 3, 1, 8, 6, 4, 2, 9]
8) [8, 7, 6, 5, 4, 3, 2, 1, 9]
9) [9, 9, 9, 9, 9, 9, 9, 9, 9]
, 1 8, 2 7, 3 6, 4 5. , , , , - 1.
, -1 - 1. 1 .
:
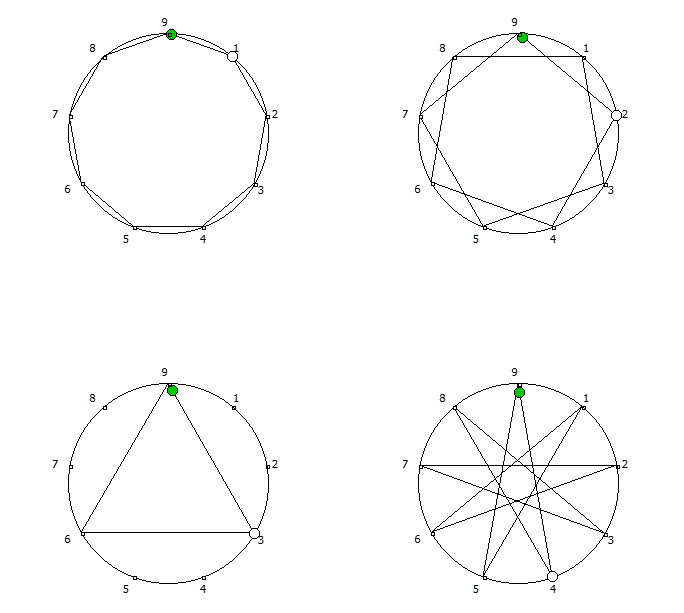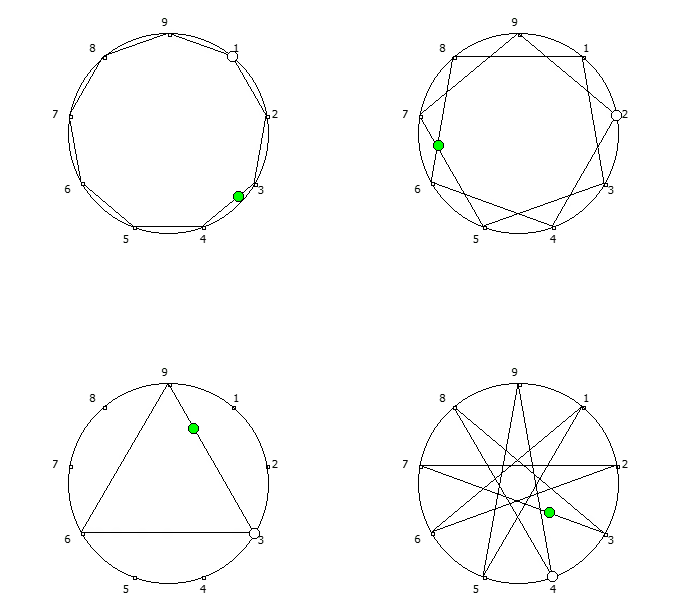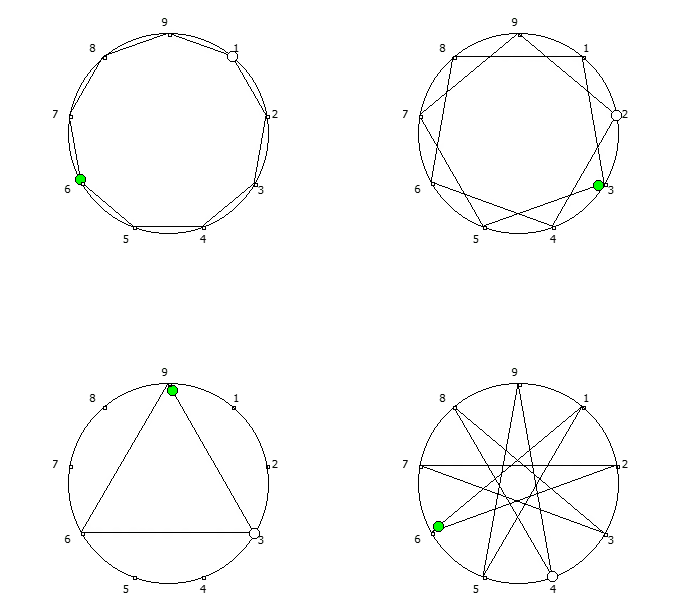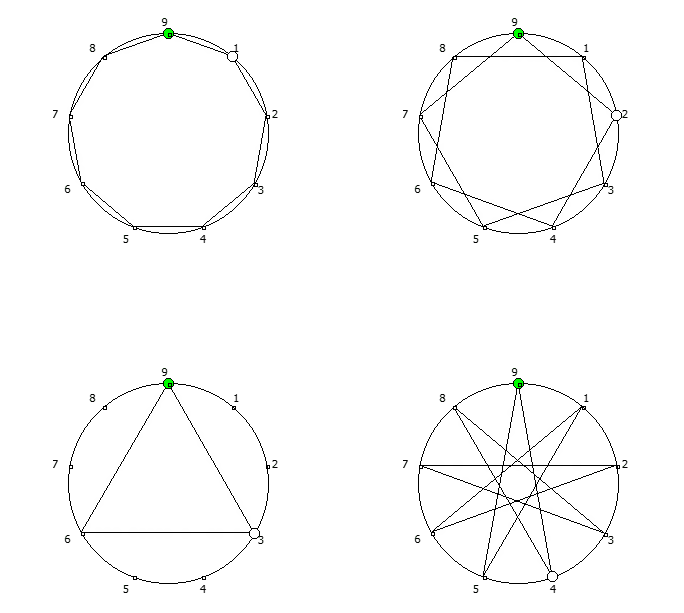
, - 1, n-. , - 1, 3 6.
:
, .
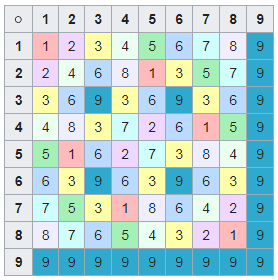
. , , - 1.
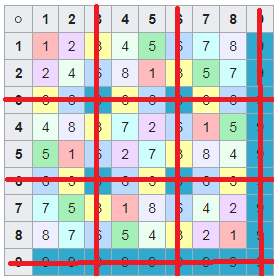
:
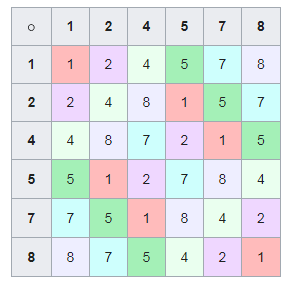
, . , , .
100 1000. - - 1, - , 1.

. .
, , , .
, , 2, 5, 4, 8.
, , 1000; 1000 1, .

base = 10
divisors = [2, 4, 5, 8]
for j in divisors:
print()
for i in range(1, base):
value = (digitalRoot(int((i / j) * (base ** 3)), base))
print('dr(',i, '/', j, ') =', value, ' ', end='')
. 9 , , 9. 3 6, , .
:
2) [5, 1, 6, 2, 7, 3, 8, 4, 9] - 5
4) [7, 5, 3, 1, 8, 6, 4, 2, 9] - 7
5) [2, 4, 6, 8, 1, 3, 5, 7, 9] - 2
8) [8, 7, 6, 5, 4, 3, 2, 1, 9] - 8
, .
:

base = 10
.
for i in range(2, base - 2):
print()
for j in range(1, base - 1):
print('dr(', j ,'^', i, ') =', digitalRoot(i ** j, base), ' ', end='')
.
, , - full reptend prime.
, . , : , p^n + 1, p — , n - .
8, [1, 3, 2, 6, 4, 5]. .
![1 7 . [1, 3, 2, 6, 4, 5]. 1 7 . [1, 3, 2, 6, 4, 5].](https://habrastorage.org/getpro/habr/upload_files/740/9dc/7d8/7409dc7d835e4080385e4973454b939c.png)
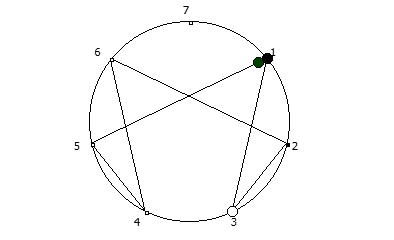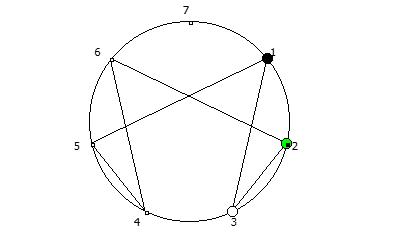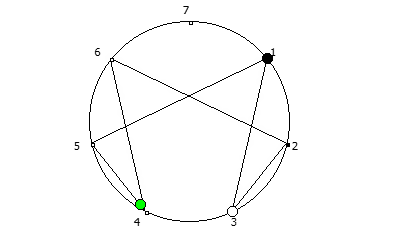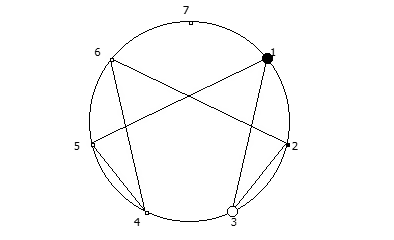
, :
, , 1/P, P - full reptend prime.
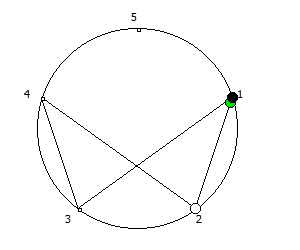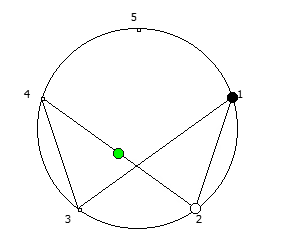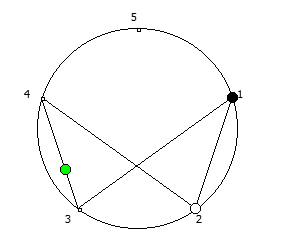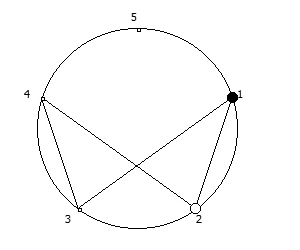
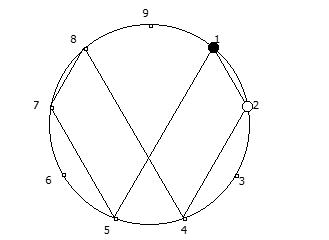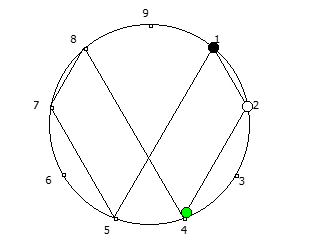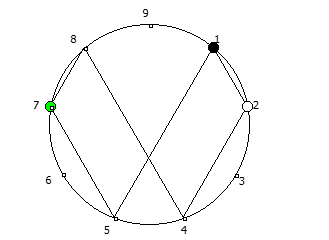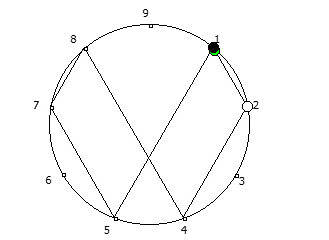
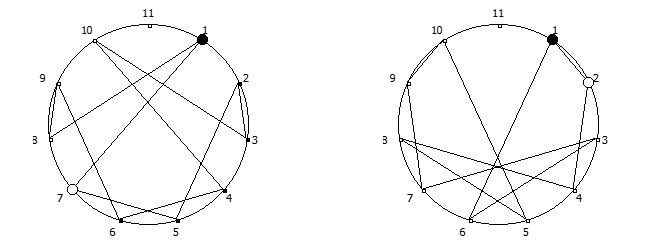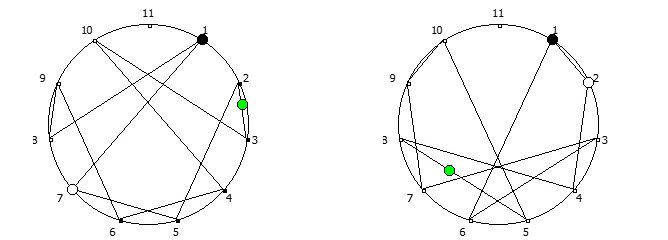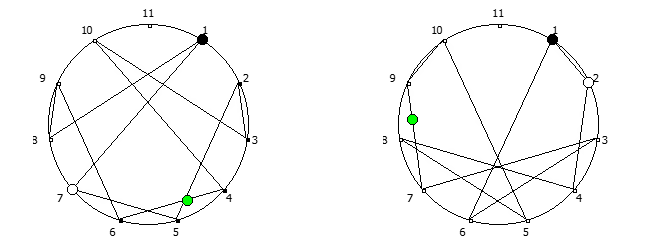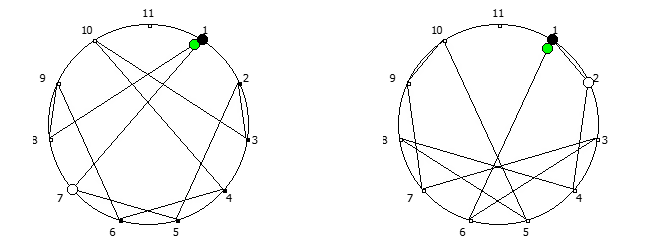
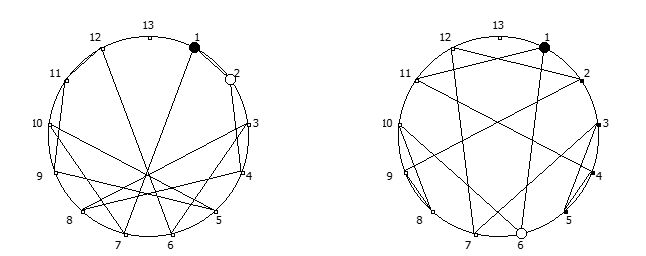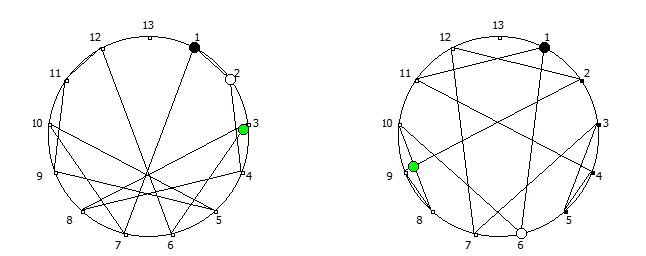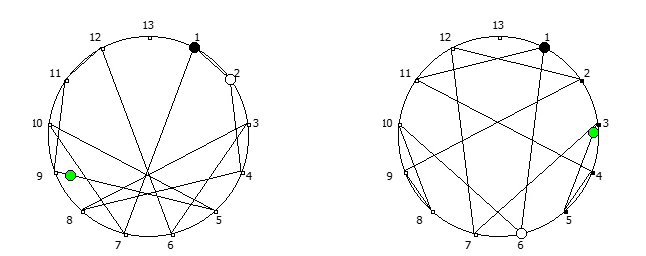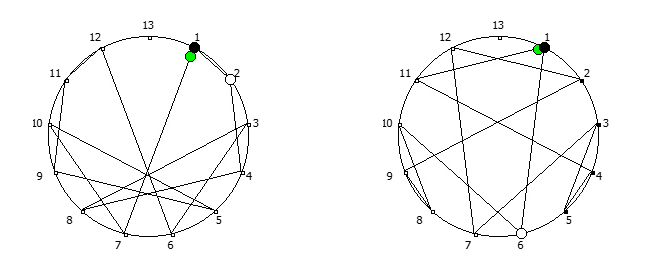
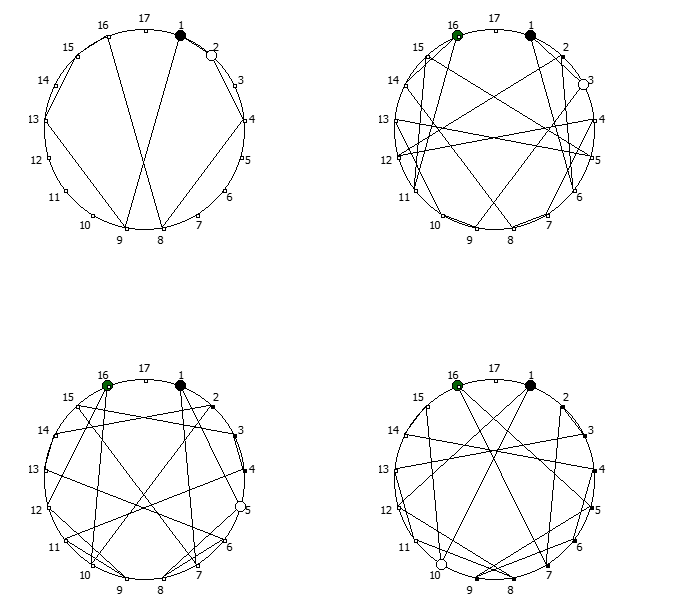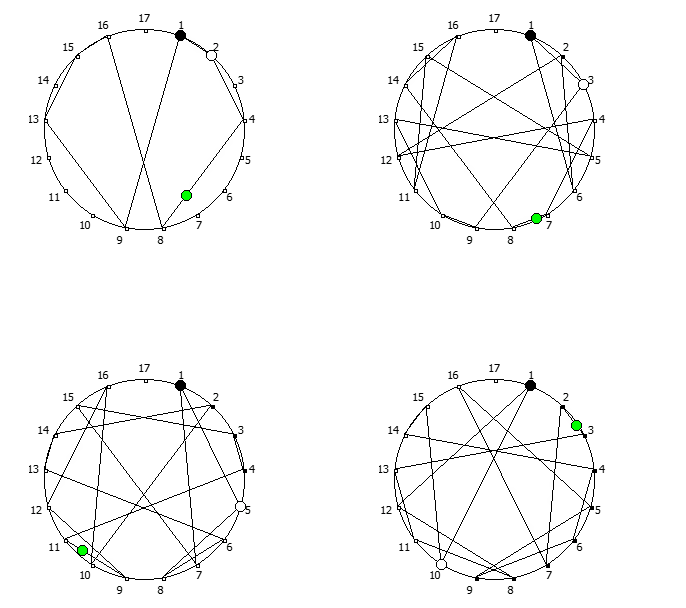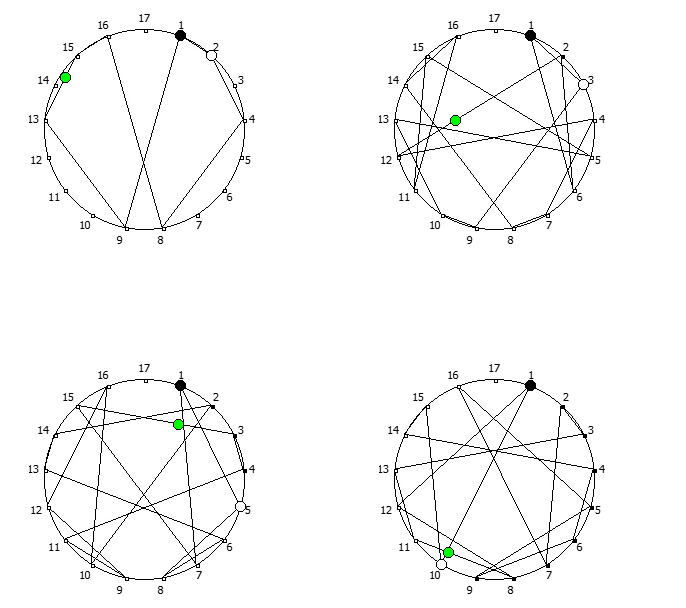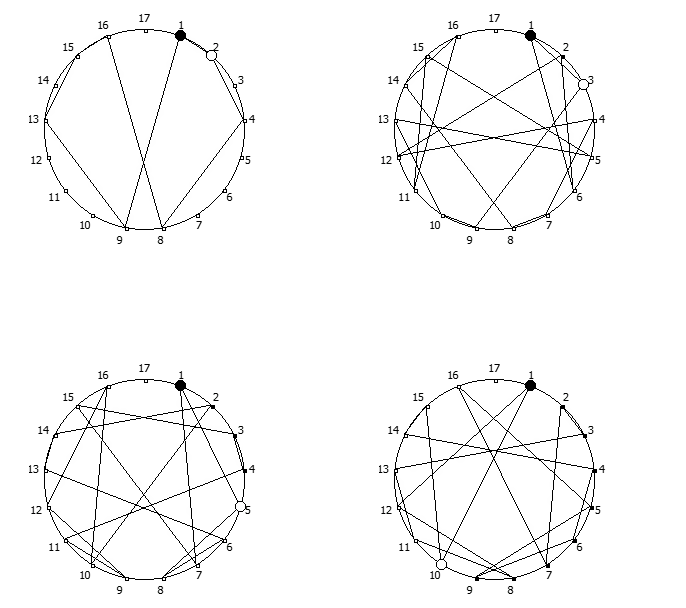
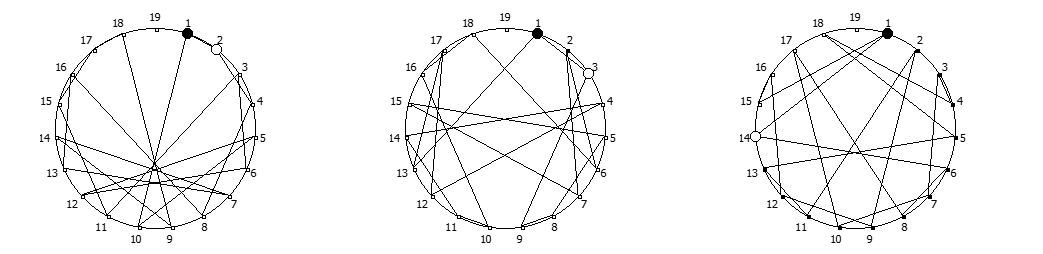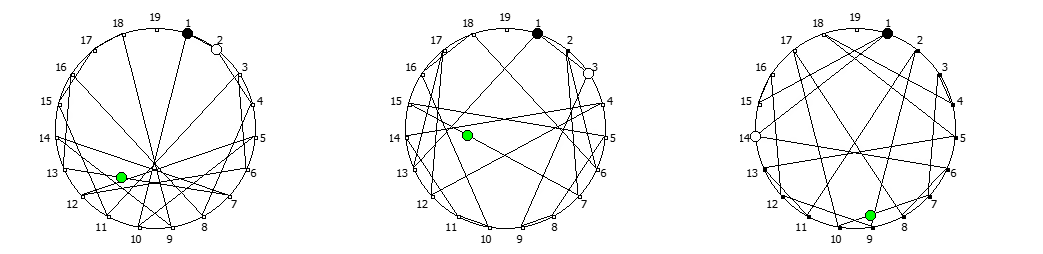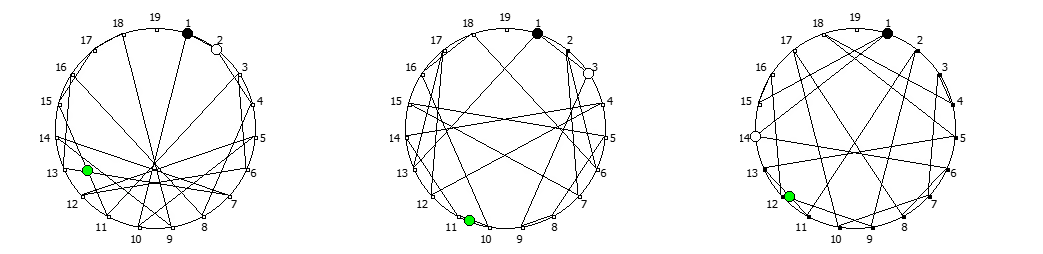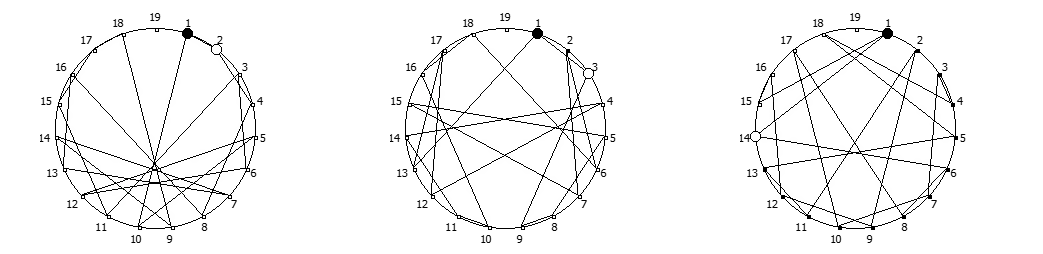
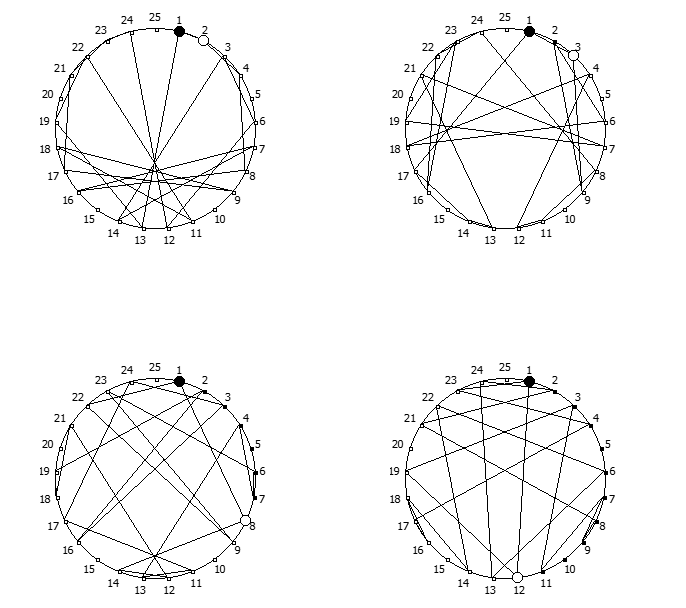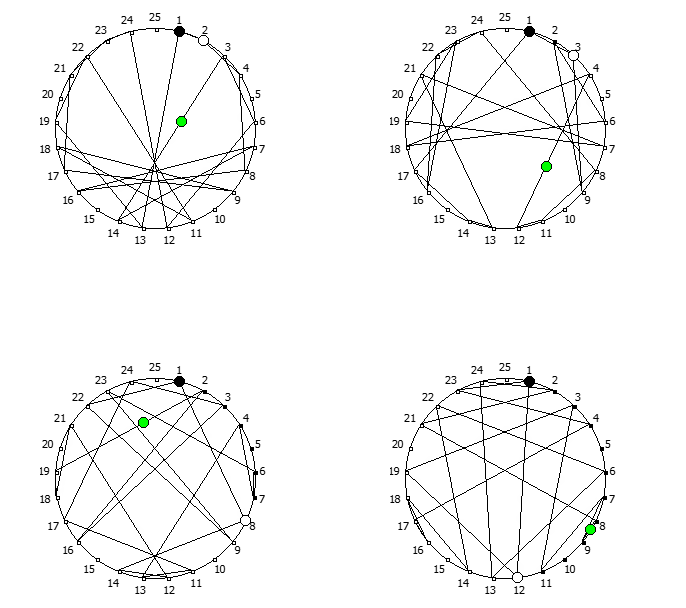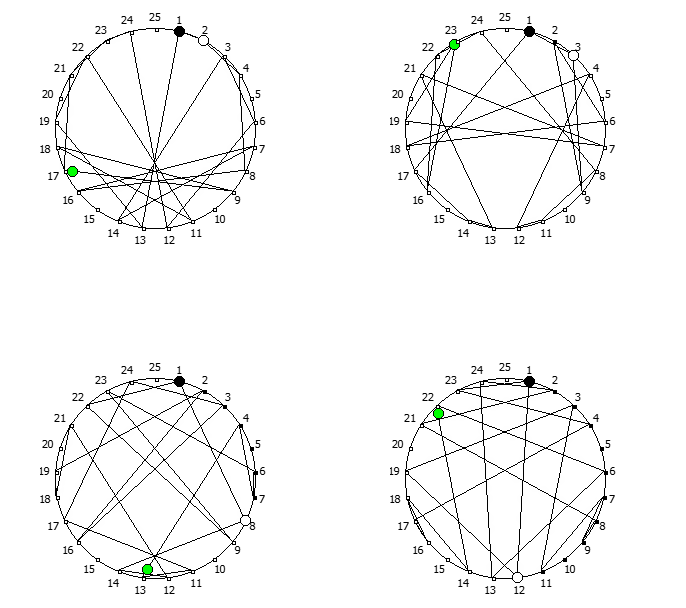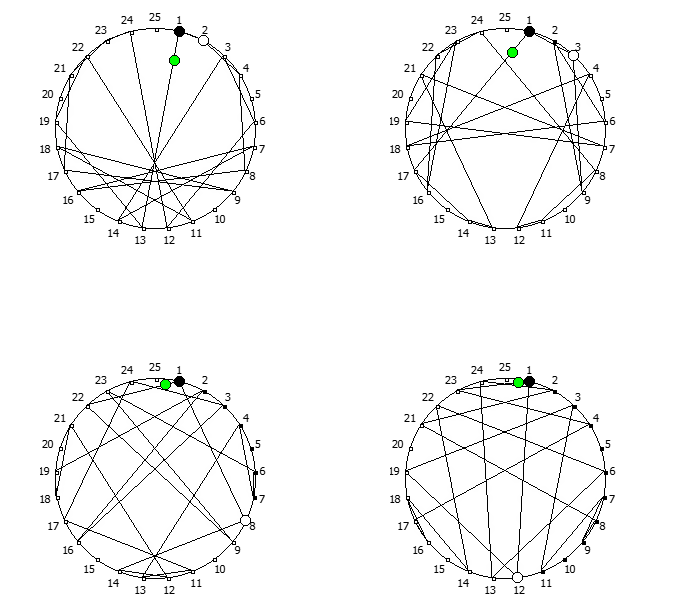

, , :
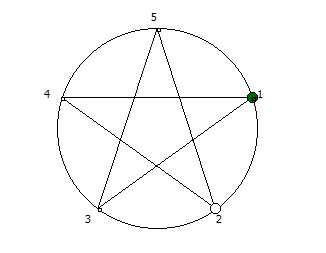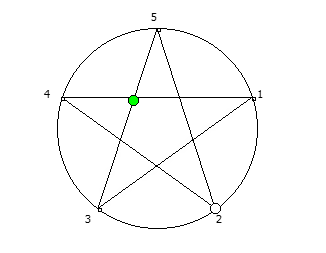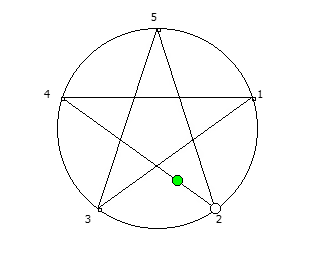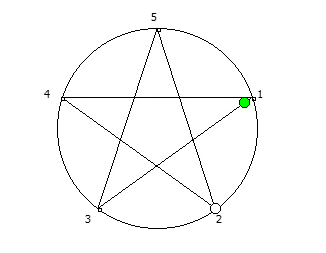
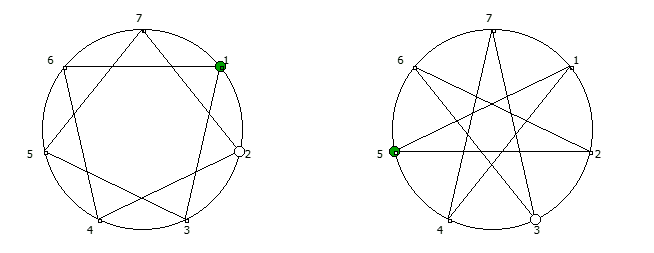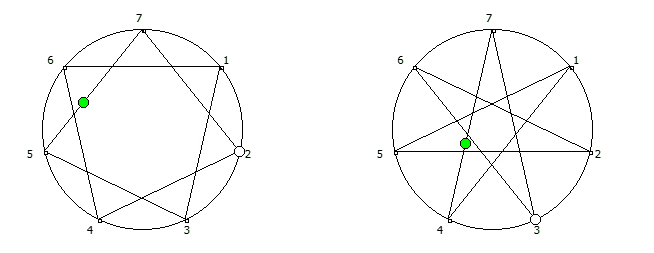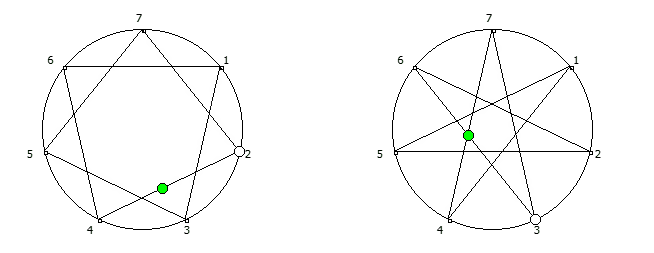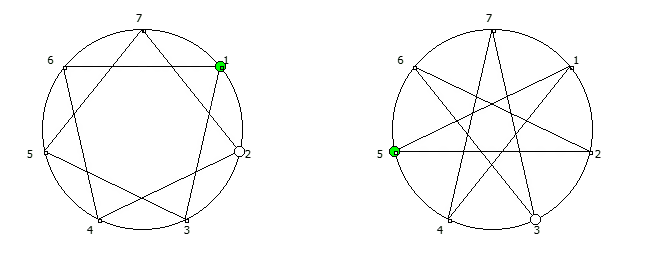
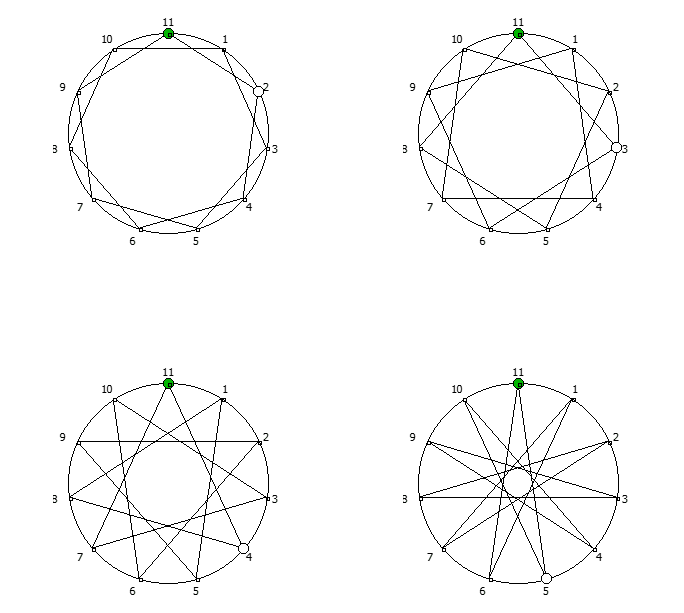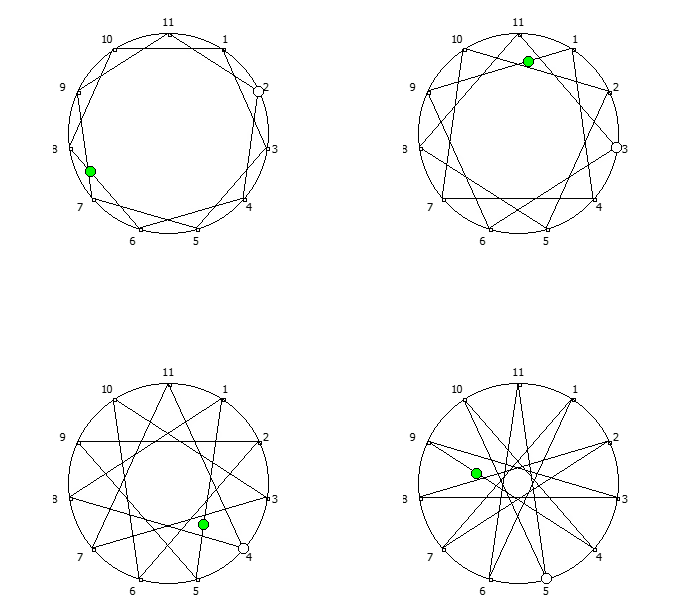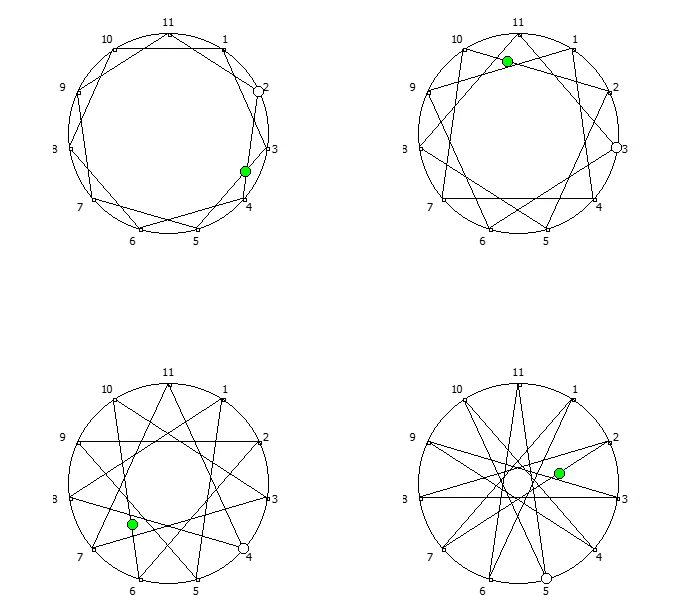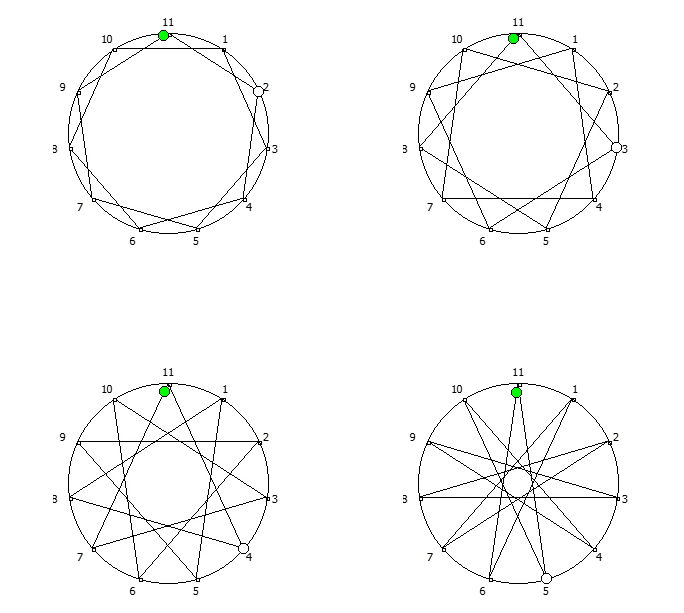
, :
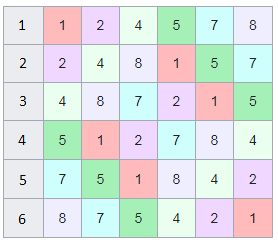
, . , [1, 3, 2, 6, 4, 5]. :
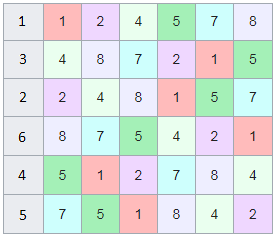
, 142857.
, , .
, n- , \ :)



, !
, , 90 1/91..90/91:
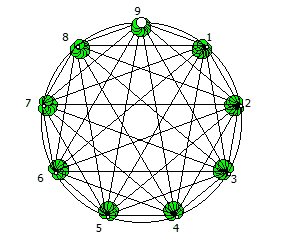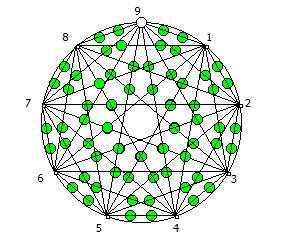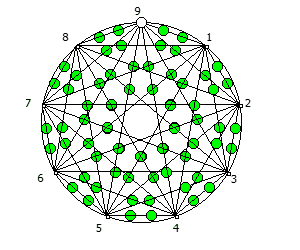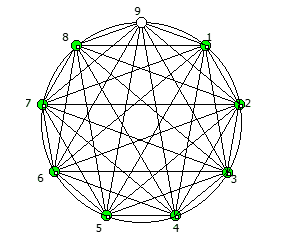
- , , !
Espero que te interese, ¡muchas gracias por tu atención!