🏇🏾 🎫 👋🏾 Una nueva clase de números primos que descubrí por accidente. ✉️ 🚿 😹

¡Hola a todos! Esta es mi primera publicación sobre Habré, así que me presentaré: mi nombre es Kostya, soy un desarrollador de C ++, un poco músico, un ingeniero principiante de ML y un amante de las matemáticas. Como puede imaginar, esta publicación tratará sobre mi afición por las matemáticas.

UPD: Se han agregado conclusiones. Un poco más tarde, agregaré ejemplos de otros números primos y otros sistemas numéricos que se utilizarán para generar números cíclicos y, como consecuencia, números primos cíclicos.

Antecedentes: hace unos 14 años, me encontré con el fenómeno de los números cíclicos, me fascinaron los patrones que se forman en ellos y me prometí explicarlos. Al principio, hice intentos ingenuos de análisis, que arrojaron resultados muy mediocres, pero en 2016 pude ver por mí mismo que la fracción racional 1/7 se puede representar mediante una progresión geométrica convergente. Para ser honesto, en ese momento ni siquiera entendí que era una progresión geométrica, pero lo reconocí visualmente. En 2018, decidí poner todas mis habilidades y diligencia para encontrar tantos patrones de números cíclicos como fuera posible. Encontré mucho, pero ahora quiero compartir lo que considero que es el más importante e, irónicamente, encontré por accidente: una nueva clase de números primos.

Estaba investigando números primos de repetición completa, y para ser más precisos, tales sistemas numéricos para números primos, en los que 1 / P, donde P es un número primo, dará una fracción periódica, cuyo período será igual a el número cíclico.

Aquí probablemente debería dar la definición misma de un número cíclico:

Un número cíclico es un número entero cuyas permutaciones cíclicas son el producto de ese número y números consecutivos.

— 142857, "" + . , . , , , . , " . ".

142857 * 2 = 285714

142857 * 3 = 428571

142857 * 4 = 571428

142857 * 5 = 714285

142857 * 6 = 857142

, 142857 2 6, 142857. .

, 1/7 . 1/7, . .

1/7 . ! , , - , .

, , , 7 . - .

, full reptend prime, «The Philisophy of Arithmetic: Exhibiting a Progressive View on the Theory and Practice of Calculation».

200 , . « », 1/7 .

«History of the Theory of Numbers» , full reptend prime.

«The Penguin Dictionary of Curious and Interesting Numbers» repunit.

«The Book of Numbers» , .

, , , , . .

, 142857, 1428571, . . , 1428571 1, — 7.

, 142857, ( 10 ). , .

7 , 142857: 1428571, 71428571, 7142857142857, 571428571428571, 1428571428571428571428571, 28571428571428571428571428571, 7142857142857142857142857142857.

: 7, 8, 13, 15, 25, 29, 31.


2	34
4	41
7	104
5	273
5	304
1	355
7	440
7	571
1	823
7	2215
5	2523
4	4379
2	4510
4	7553
4	7679
7	9536

23 , 10¹⁰⁰⁰.

. Full reptend prime

, , , , .

full reptend prime long prime. . , , full reptend .

full reptend

P — , , 1/P, N , P-1, , P N full reptend.

P full reptend N, P-1 .

P, , . P, - , P - full reptend prime.

P = 7 . 1/P = 0,(142857). 6, P-1. 1/P .. P-1/P:

2/P = 0,(285714)

3/P = 0,(428571)

4/P = 0,(571428)

5/P = 0,(714285)

6/P = 0,(857142)

, . . , . , . - 1/P. full reptend.

P 1/P. P. P = 2 2, P = 3 3, ..

( ⁿ) mod P = 1

P :

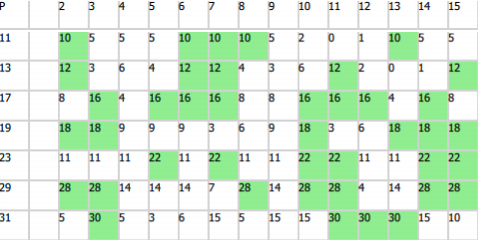
, , full reptend, 7, 17, 19, 23, 29. 2 5 , .

P = 3 : 1/3 = 0,(3). P = 11 , 2 : 1/11 = 0,(09).

P = 13 , 6, P-1. (P-1)/2, , . P 2nd reptend level prime. 2nd reptend level prime:

1/13 = 0,(076923)

2/13 = 0,(153846)

P = 13, P-1/P, , 1/13 2/13, .

3/13 = 0,(230769) — 1

4/13 = 0,(307692) — 1

5/13 = 0,(384615) — 2

6/13 = 0,(461538) — 2

7/13 = 0,(538461) — 2

8/13 = 0,(615384) — 2

9/13 = 0,(692307) — 1

10/13 = 0,(769230) — 1

11/13 = 0,(846153) — 2

12/13 = 0,(923076) — 1

2nd reptend level prime : .

.. : 769230769, 769230769230769230769,769230769230769230769230769230769.

: 1538461.

, , full reptend prime, . P = 7 2 , full reptend, 3 5 — .

7 . 12, . , 17 19, 59 61.

, full reptend n-th repntend level . P N .

1/P:

$\ begin {ecuación} \ sum \ limits_ {n = 0} ^ \ infty \ frac {s * r ^ n} {base ^ {length (n + 1)}} = \ frac {1} {P} \ end { ecuación}$

s — , 1/P:

$\ begin {ecuación} s = [\ frac {1} {P} * base ^ {longitud}] \ end {ecuación}$

full reptend prime , 1 . :)

length , s, . length .

r , 1/P. 1/P P-1, full reptend , P-1.

, , , . P= 7, .. full reptend .

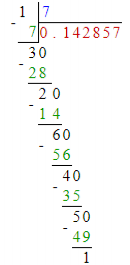
: [3, 2, 6, 4, 5, 1]. . base mod P. , :

$\ begin {ecuación} \ begin {casos} r_0 = 1 \\ r_n = r_ {n-1} * (base \ mod P) \\ \ end {casos} \ end {ecuación}$

$\ begin {ecuación} r_ {longitud} = base ^ {longitud} \ mod P \ end {ecuación}$

, : P— ; base — ; length — , .

$\ begin {ecuación} \ frac {1} {P} = \ sum \ limits_ {n = 0} ^ \ infty \ frac {[\ frac {1} {P} * base ^ {length}] * (base ^ { longitud} \ mod P) ^ n} {base ^ {longitud (n + 1)}} \ end {ecuación}$

P = 7 c s, :

$\ begin {ecuación} \ frac {1} {7} = \ suma \ límites_ {n = 0} ^ \ infty \ frac {1 * 3 ^ n} {10 ^ {n + 1}} \ end {ecuación}$

s = 1, 0,(142857), .. length = 1. r = 3, , length = 1.

$\ begin {ecuación} \ frac {1} {7} = 0,1 + 0,03 + 0,009 + 0,0027 + 0,00081 + .. \ end {ecuación}$

3 10. :

$\begin{equation} \frac{1}{7} = \sum\limits_{n=0}^\infty\frac{14*2^n}{10^{2(n+1)}} \end{equation}$ $\begin{equation} \frac{1}{7} = 0.14 + 0.0028 + 0.000056 + 0.00000112 + .. \end{equation}$

2 100. s = 14, 0,(142857), .. length = 2. r = 2, , length = 2. , , , .

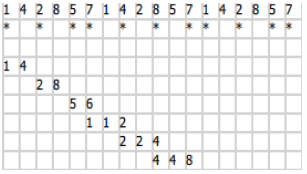
length 1:

$\begin{equation} \frac{1}{7} = \sum\limits_{n=0}^\infty\frac{142*6^n}{10^{3(n+1)}} \end{equation}$ $\begin{equation} \frac{1}{7} = \sum\limits_{n=0}^\infty\frac{1428*4^n}{10^{4(n+1)}} \end{equation}$ $\begin{equation} \frac{1}{7} = \sum\limits_{n=0}^\infty\frac{14285*5^n}{10^{5(n+1)}} \end{equation}$ $\begin{equation} \frac{1}{7} = \sum\limits_{n=0}^\infty\frac{142857*1^n}{10^{6(n+1)}} \end{equation}$

, s :

$\begin{equation} \frac{1}{7} = \sum\limits_{n=0}^\infty\frac{1428571*3^n}{10^{7(n+1)}} \end{equation}$

s - , . . .

, , , s P N — .

P = 17:

$\begin{equation} \frac{1}{17} = \sum\limits_{n=0}^\infty\frac{5*15^n}{10^{2(n+1)}} \end{equation}$ $\ begin {ecuación} \ frac {1} {17} = \ sum \ limits_ {n = 0} ^ \ infty \ frac {58 * 14 ^ n} {10 ^ {3 (n + 1)}} \ end { ecuación}$ $\ begin {ecuación} \ frac {1} {17} = \ sum \ limits_ {n = 0} ^ \ infty \ frac {588 * 4 ^ n} {10 ^ {4 (n + 1)}} \ end { ecuación}$

89 . 1/89 = 0,0112359.. — , . , :

$\ begin {ecuación} \ frac {1} {89} = \ sum \ limits_ {n = 0} ^ \ infty \ frac {1 * 11 ^ n} {10 ^ {2 (n + 1)}} \ end { ecuación}$ $\ begin {ecuación} \ frac {1} {89} = \ suma \ límites_ {n = 0} ^ \ infty \ frac {Fibonacci (n)} {10 ^ {n + 1}} \ end {ecuación}$

, — 109.

1/89 : (-1)ⁿ⁺¹. , , .

$\ begin {ecuación} \ frac {1} {109} = \ sum \ limits_ {n = 0} ^ \ infty \ frac {9 * 17 ^ n} {10 ^ {3 (n + 1)}} \ end { ecuación}$ $\ begin {ecuación} \ frac {1} {109} = \ sum \ limits_ {n = 0} ^ \ infty \ frac {Fibonacci (n) * (- 1) ^ {n + 1}} {10 ^ {n +1}} \ end {ecuación}$

, , .

-

s , , .

, P = 7, 142857, 1428571. , , 1/P, 1/P .. P-1/P. , , 71428571.

, . , . , , , , , .

, s, , , , . - .

P = 7. 1/P, P-1/P, , s : 2, 5, 7, 71, 571, 2857, 28571.

, - .

- P N. , full reptend prime .

,

, . P N, . , P, , .

- :

, P, , . , 142857. 40 5SMYBH ( 5, 28, 22, 34, 11, 17).

, , H5SMYBH 40 , , : 70217142857.

, . , , , .

P=7 N=10:

1) 1428571

2) 71428571

3) 7142857142857

4) 571428571428571

5) 1428571428571428571428571

6) 28571428571428571428571428571

7) 7142857142857142857142857142857

8) 2857142857142857142857142857142857

9) 42857142857142857142857142857142857142857

40 :

1) MCYB

2) Ra2YB

3) 13NYIMYBH

4) 277Sb5SMYB

5) 1D8TJS2CYBH5SMYB

6) GP98QAT0SMYBH5SMYB

7) 2NbRO471EIMYBH5SMYBH

8) PdGa11UDOPSMYBH5SMYBH

9) 3WAEQ3OR61AQVH5SMYBH5SMYBH

P=7 N=10 :

1) H5SMYBH

2) - 77 , 5SMYBH, B:

5SMYBH5SMYBH5SMYBH5SMYBH5SMYBH5SMYBH5SMYBH5SMYBH5SMYBH5SMYBH5SMYBH5SMYBH5SMYB

1) 70217142857

– 12 , 123 .

2) 3262280440470765442418939358741703168874849426...

...28571428571428571428571428571428571428571428571428571428571428571428571428571

- , .

,

P = 7 N = 10. :

Ns(i) = N + 3*N*i + ((i + 1) % 2) * i*N*4

i — . i = 0 , full reptend prime. .

, , .

N = 3, 10, 17, 31, 38, 59:

Ns(i) = N + 3*N*i + ((i + 1) % 2) * i*N

N = 5, 19, 26, 33, 47, 61:

Ns(i) = N + N*i + ((i + 1) % 2) * i*5*N

N = 12:

Ns(i) = N + N*i + ((i + 1) % 2) * i*5*N

N = 40 , N = 10.

N = 24, N = 12.

, , N.

, 40 , . , , - , 40, , 40 .

12 24 . , , , 12.

, , , full reptend.

, , , 40 10 .

P = 5, . P = 17 , , base, base*2, base*4, .

, , .

, , . . .

, , . . : , , , , .

#1: 40 . 1/7₄₀=0.(5SMYBH)₄₀, H5SMYBH₄₀, 70217142857. 7142857, 40 .

#2: 10 . 571428571428571. 40 1D8TJS2CYBH5SMYB₄₀. , YBH5SMYB , .

,

, . . , .

, . , .

, full reptend prime .

. , , github. .

, full reptend prime. .

, , , .

, 2019 , \ .

, , arxiv.org – . , . – :

, arxiv ? ? 6- , .

¡Gracias a todos por su atención! Espero que mi primer artículo no haya sido agotador, hay algunos más por delante y no todos serán sobre matemáticas.

Una nueva clase de números primos que descubrí por accidente.

. Full reptend prime

full reptend

-

,

,

,

More articles: