❓ 🛸 🤨 Opciones matemáticas o modelo Black-Scholes 👼🏽 👇🏽 🎦

El interés general en el modelo Black-Scholes (en adelante, BS) se debe a que en un momento sus autores revolucionaron el campo de la evaluación del valor razonable de opciones y otros instrumentos financieros derivados. Posteriormente recibieron el Premio Nobel por sus descubrimientos, y la fórmula analítica que derivaron se convirtió, quizás, en la más fundamental y conocida en el mundo de las finanzas.

El modelo BS no es menos interesante desde el punto de vista del análisis matemático y teórico probabilístico de bajo nivel. El artículo analiza en detalle el proceso de fundamentación de los principios básicos y clave del modelo BS, y también deduce una fórmula analítica que se utiliza para evaluar el valor razonable de las opciones.

Conceptos básicos

Opción: contrato mediante el cual el comprador de una opción recibe el derecho , pero no la obligación, de comprar o vender un activo determinado a un precio predeterminado, que se denomina precio de ejercicio o precio de ejercicio.

A los efectos de un análisis más detallado, dicho instrumento financiero se representa con mayor precisión como una función que describe los pagos de la opción en el momento del vencimiento del contrato. Para una comprensión más simple e intuitiva, consideraremos una opción del tipo Llamada, cuya función de pago es la siguiente.

donde es el precio del activo subyacente, el precio del ejercicio.

Desde un punto de vista práctico, la función asume que el comprador de la opción se beneficiará si el precio del activo subyacente supera el precio de ejercicio x_s y que coincide con la diferencia [x-x_s] . De lo contrario, el tenedor de la opción recibirá una pérdida equivalente a la prima pagada por la compra del contrato de opción.

, . , . , , ( ).

, C = máximo (x - x_s; 0) , , , , .

, , , . , .

, C = máximo (x - x_s; 0) x (t) . , x (t) , : $dx = xrdt + x \ sigma \ delta W$ *. , .

$dC = \left(\frac{\partial C}{\partial t} + xr\frac{\partial C}{\partial x} + \frac{\sigma^2}{2} \frac{\partial ^2 C}{\partial x^2}\right)dt + x\sigma\frac{\partial C}{\partial x} \delta W \qquad (1)$

, . (1) , . - .

$\Pi = \frac{\partial C}{\partial x} \cdot x - C(x, t) \qquad (2)$

, $\Delta = \frac{\partial C}{\partial x}$ - .

, , $\Delta = const$ - : $d \Pi = \Delta \cdot dx - dC$ . , , *, (1) . :

$d \Pi = \Delta(xrdt + x\sigma \delta W) - \left [ \left(\frac{\partial C}{\partial t} + xr\frac{\partial C}{\partial x} + \frac{\sigma^2}{2} \frac{\partial ^2 C}{\partial x^2}\right)dt + x\sigma\frac{\partial C}{\partial x} \delta W \right ] \qquad (3)$

, $\Delta = \frac{\partial C}{\partial x}$ , $x\sigma\frac{\partial C}{\partial x} \delta W$ :

$d \Pi = - \left [\frac{\partial C}{\partial t} + \frac{\sigma^2}{2} \frac{\partial ^2 C}{\partial x^2}\right]dt \qquad (4)$

, . $\tau$ , $\tau = T-t$ , . , , $\tau$ , . , : $\frac{\partial C}{\partial t } = - \frac{\partial C}{\partial \tau }$ .

B,S - : $d \Pi = \Pi rdt$ , . (4) , $\Pi$ (2) .

$\frac{\partial C}{\partial \tau }dt - \frac{\sigma^2}{2} \frac{\partial ^2 C}{\partial x^2}dt =\left( \frac{\partial C}{\partial x} \cdot x - C(x, t) \right ) rdt$

, :

$\frac{\partial C}{\partial \tau } + rC = \frac{\sigma^2 x^2}{2} \frac{\partial ^2 C}{\partial x^2} + rx\frac{\partial C}{\partial x } \qquad (5)$

, . , , , .

. $y = \ln x$ . x^2 , .

, , x^2 , :

$\frac{\partial C}{\partial \tau } + rC = \frac{\sigma^2}{2} \frac{\partial ^2 C}{\partial y^2} + R\frac{\partial C}{\partial y } \qquad (6)$

$R = r - \frac{\sigma^2}{2}$

, $y = \ln x$

$\frac{\partial C}{\partial x} = \frac{\partial C}{\partial y} \cdot \frac{dy}{dx} = \frac{\partial C}{\partial y} \cdot \frac{1}{x}$

, $y = \ln x$

$\frac{\partial ^2 C}{\partial x^2} =\left ( \frac{\partial C}{\partial y} \cdot \frac{dy}{dx}\right )_x '= (\frac{\partial C}{\partial y})_x '\cdot \frac{dy}{dx} + \frac{\partial C}{\partial y} \cdot (\frac{dy}{dx})_x' = \left( (\frac{\partial C}{\partial y})_y' \cdot y'\right ) \cdot y'+ \frac{\partial C}{\partial y} \cdot y'' =$ $= \left( \frac{\partial^2 C}{\partial y^2} \frac{1}{x}\right ) \frac{1}{x} - \frac{\partial C}{\partial y} \frac{1}{x^2} = \frac{1}{x^2}\left ( \frac{\partial^2 C}{\partial y^2} - \frac{\partial C}{\partial y}\right )$

$\frac{\partial C}{\partial \tau } + rC = \frac{\sigma^2 x^2}{2} \cdot \frac{1}{x^2}\left ( \frac{\partial^2 C}{\partial y^2} - \frac{\partial C}{\partial y}\right ) + rx \cdot \frac{1}{x} \frac{\partial C}{\partial y} \Leftrightarrow \frac{\partial C}{\partial \tau } + rC = \frac{\sigma^2}{2} \left( \frac{\partial ^2 C}{\partial y^2} -\frac{\partial C}{\partial y } \right )+ r\frac{\partial C}{\partial y }$

$\frac{\partial C}{\partial \tau } + rC = \frac{\sigma^2}{2} \left( \frac{\partial ^2 C}{\partial y^2} -\frac{\partial C}{\partial y } \right )+ r\frac{\partial C}{\partial y } \Rightarrow_1 \frac{\partial C}{\partial \tau } + rC = \frac{\sigma^2}{2} \frac{\partial ^2 C}{\partial y^2} - \frac{\sigma^2}{2} \frac{\partial C}{\partial y } + r\frac{\partial C}{\partial y } \Rightarrow_2$ $\frac{\partial C}{\partial \tau } + rC = \frac{\sigma^2}{2} \frac{\partial ^2 C}{\partial y^2} + (r - \frac{\sigma^2}{2}) \frac{\partial C}{\partial y } \Rightarrow_3 \frac{\partial C}{\partial \tau } + rC = \frac{\sigma^2}{2} \frac{\partial ^2 C}{\partial y^2} + R\frac{\partial C}{\partial y }$

$R = r - \frac{\sigma^2}{2}$

, . : $C(e^y, \tau) = e^{\alpha y + \beta \tau} \cdot U(y, \tau)$ , $\alpha$ $\beta$ , , :

$\frac{\partial U}{\partial \tau } = \frac{\sigma^2}{2} \frac{\partial ^2 U}{\partial y^2} \qquad (7)$

$Ue^{\alpha y + \beta \tau}$

$\left (U e^{\alpha y + \beta \tau} \right )_\tau ' + rUe^{\alpha y + \beta \tau} = \frac{\sigma^2}{2} \left (U e^{\alpha y + \beta \tau} \right )_{yy} '' + R\left (U e^{\alpha y + \beta \tau} \right )_y ' \qquad (*)$

$\tau$

$\left (U e^{\alpha y + \beta \tau} \right )_\tau ' = \frac{\partial U}{\partial \tau} \cdot e^{\alpha y + \beta \tau} + U \cdot \left ( e^{\alpha y + \beta \tau} \right )_\tau ' = \frac{\partial U}{\partial \tau} \cdot e^{\alpha y + \beta \tau} + \beta U \cdot e^{\alpha y + \beta \tau}$

$\left (U e^{\alpha y + \beta \tau} \right )_y ' = \frac{\partial U}{\partial y} \cdot e^{\alpha y + \beta \tau} + U \cdot \left ( e^{\alpha y + \beta \tau} \right )_y ' = \frac{\partial U}{\partial y} \cdot e^{\alpha y + \beta \tau} + \alpha U \cdot e^{\alpha y + \beta \tau}$

$\left( { \frac{\partial U}{\partial y}} \cdot e^{\alpha y + \beta \tau} + \alpha U \cdot e^{\alpha y + \beta \tau} \right)_y '= \left( { \frac{\partial U}{\partial y}} \cdot e^{\alpha y + \beta \tau} \right)_y' + \left (\alpha U \cdot e^{\alpha y + \beta \tau} \right )_y' =$ $\left( { \frac{\partial^2 U}{\partial y^2}}e^{\alpha y + \beta \tau} + \alpha \frac{\partial U}{\partial y} e^{\alpha y + \beta \tau} \right) + \left ( \alpha \frac{\partial U}{\partial y} e^{\alpha y + \beta \tau} + \alpha^2 U e^{\alpha y + \beta \tau}\right ) =$ $e^{\alpha y + \beta \tau} \left( \frac{\partial^2 U}{\partial y^2} + 2\alpha \frac{\partial U}{\partial y} + \alpha^2 U \right)$

$e^{\alpha y + \beta \tau}$

$\frac{\partial U}{\partial \tau} + \beta U + rU = \frac{\sigma^2}{2}\left( \frac{\partial^2 U}{\partial y^2} + 2\alpha \frac{\partial U}{\partial y} + \alpha^2 U \right) + R\left ( \frac{\partial U}{\partial y} + aU \right )$

$\alpha = -\frac{R}{\sigma^2}$ , $\beta = -(r + \frac{R^2}{2 \sigma^2})$ , :

$\frac{\partial U}{\partial \tau} - (r + \frac{1}{2}\frac{R^2}{\sigma^2}) U + rU = \frac{\sigma^2}{2}\left( \frac{\partial^2 U}{\partial y^2} - \frac {2R}{\sigma^2} \frac{\partial U}{\partial y} + \frac{R^2}{\sigma^4} U \right) + R\left ( \frac{\partial U}{\partial y} - \frac{R}{ \sigma^2}U \right )$

$\frac{\partial U}{\partial \tau } = \frac{\sigma^2}{2} \frac{\partial ^2 U}{\partial y^2}$

(7) :

$P(y, \tau, y_0) = \frac{1}{\sigma \sqrt{2 \pi \tau }} \cdot \exp(-\frac{(y-y_0)^2}{2\sigma^2 \tau}) \qquad (8)$

$(P)_\tau '$ , $(P)_{yy} ''$ (7) .

$e^{*} = \exp(-\frac{(y-y_0)^2}{2\sigma^2 \tau})$

$\tau$ :

$\frac{\partial P}{\partial \tau} = \left (\frac{1}{\sigma \sqrt{2 \pi \tau }} \right )_ \tau ' \cdot e^{*} + \frac{1}{\sigma \sqrt{2 \pi \tau }} \cdot \left (\exp(-\frac{(y-y_0)^2}{2\sigma^2 \tau}) \right )_\tau ' =$ $- \frac{1}{2\sigma \tau \sqrt{2\pi \tau}} \cdot e^{*} + \frac{1}{\sigma \sqrt{2\pi \tau}}\cdot e^{*} \cdot \frac{(y-y_0)^2}{2\sigma^2 \tau^2} = e^{*} \left (\frac{(y-y_0)^2}{2 \sigma^3 \tau^2 \sqrt{2\pi \tau}} - \frac{1}{2\sigma \tau \sqrt{2\pi \tau}} \right )$

$\frac{\partial P}{\partial y} = \frac{1}{\sigma \sqrt{2\pi \tau}} \cdot (e^{*})_y' = - \frac{1}{\sigma \sqrt{2\pi \tau}} \cdot e^{*} \cdot \frac{(y-y_0)}{ \sigma^2 \tau} \Rightarrow$ $\frac{\partial^2 P}{\partial y^2} = \left (- \frac{1}{\sigma \sqrt{2\pi \tau}} \cdot e^{*} \cdot \frac{(y-y_0)}{\sigma^2 \tau} \right )_y' = \left (- \frac{1}{\sigma^3 \tau \sqrt{2\pi \tau}} \cdot \left ( e^{*} \cdot (y-y_0) \right ) \right )_y' =$ $- \frac{1}{\sigma^3 \tau \sqrt{2\pi \tau}} \cdot \left[\left( e^{*} \cdot (-\frac{(y-y_0)}{\sigma^2 \tau}) \cdot (y-y_0) \right ) + e^{*} \cdot 1\right] = e^{*} \cdot \left (\frac{(y-y_0)^2}{\sigma^5 \tau^2 \sqrt{2\pi \tau}} - \frac{1}{\sigma^3 \tau \sqrt{2\pi \tau}} \right )$

(7) e^* . :

$\frac{(y-y_0)^2}{2 \sigma^3 \tau^2 \sqrt{2\pi \tau}} - \frac{1}{2\sigma \tau \sqrt{2\pi \tau}} = \frac{\sigma^2}{2}\left (\frac{(y-y_0)^2}{\sigma^5 \tau^2 \sqrt{2\pi \tau}} - \frac{1}{\sigma^3 \tau \sqrt{2\pi \tau}} \right )$

, u(s) :

$\int_ {-\infty}^{+\infty} u(s) P(y, \tau, s)ds,$

$\tau$ , (7) , - . , (7) :

$U(y, \tau) = \int_{-\infty}^{+\infty} u(s) P(y, \tau, s)ds =\frac{1}{\sigma \sqrt{2 \pi \tau }} \int_{-\infty}^{+\infty} u(s) \cdot \exp \left(-\frac{(y-s)^2}{2\sigma^2 \tau}\right)ds \qquad (9)$

(9) u(s) . , u(y) = U(y;0) . - , $\tau \mapsto 0$ - $\delta (y-s)$ :

$U(y; 0) = \int _{-\infty}^{+\infty}u(s) \delta (y-s)ds = u(y)$

: f(x) [a;b] , g(x) , $c \in[a,b]$ , :

$\int_{a}^{b} f(x)g(x) dx = f(c) \int_{a}^{b}g(x)dx$

$\varepsilon > 0$ .

$\tau \mapsto 0$ "" $\int_{-\infty}^{y- \varepsilon }, \int_{y-\varepsilon }^{+\infty}$ :

$U(y, \tau) \approx \int_{y- \varepsilon}^{y+ \varepsilon} u(s) P(y, \tau, s)ds$

$d \in [y-\varepsilon; y+\varepsilon ]$ ,

$\int_{y- \varepsilon}^{y+ \varepsilon} u(s) P(y, \tau, s)ds = u(d) \int_{y- \varepsilon}^{y+ \varepsilon} P(y, \tau, s)ds.$

, $\lim_{\tau \mapsto 0} \int_{y- \varepsilon}^{y+ \varepsilon} P(y, \tau, s)ds = 1$ , $u(d) \int_{y- \varepsilon}^{y+ \varepsilon} P(y, \tau, s)ds \approx u(d)$ . , $\varepsilon >0$ , $\tau \mapsto 0$ , $d \mapsto y$ . :

$u(y) = U(y;0) = e^{-\alpha y}\cdot C(e^{y}; 0) = e^{-\alpha y} \cdot \max (e^y -x_s;0)$

, $\max (e^y -x_s;0)=0$ $y < \ln x_s$ , (9) :

$U(y, \tau) = \int_{\ln x_s}^{+\infty} (e^s - x_s)\frac{e^{-\alpha s}}{\sigma \sqrt{2 \pi \tau}} \exp\left(-\frac{(y-s)^2}{2 \sigma^2 \tau}\right)ds \qquad (10)$

(10) $U(y;\tau)$ , , $C(e^y, \tau) = e^{\alpha y + \beta \tau} \cdot U(y, \tau)$ . , $U(y, \tau)$ $C(e^y, \tau)$ .

(10) .

, -:

$C = x_0F \left [ \frac{\ln(xe^{r\tau} / x_s)}{\sigma \sqrt{\tau}} + \frac{\sigma \sqrt{\tau}}{2} \right ] - x_se^{-r\tau}F \left [ \frac{\ln(xe^{r\tau} / x_s)}{\sigma \sqrt{\tau}} - \frac{\sigma \sqrt{\tau}}{2} \right ]$

, , $\sigma -$ .

, :

$z = \frac{(s-y)}{ \sigma \sqrt{\tau}}; \qquad s = z\sigma \sqrt{\tau} + y \qquad$ $z(\ln x_s) = \frac{\ln x_s - y}{\sigma \sqrt{\tau}} =: \gamma \text{ - }$ $dz = \left (\frac{(s-y)}{2 \sigma \sqrt{\tau}} \right )' ds \Rightarrow dz = \frac{ds}{\sigma \sqrt{\tau}} \Rightarrow ds = \sigma \sqrt{\tau}dz$

$U(y, \tau) =\int_{\gamma }^{+\infty}\left (e^{(1-\alpha)(\sqrt{\tau} \sigma z + y)} - x_s e^{-\alpha(y + \sqrt{\tau}\sigma z)} \right ) \frac{e^{-\frac{z^2}{2}}}{\sigma \sqrt{2 \pi \tau}} \sqrt{\tau }\sigma dz =$ $\frac{1}{\sqrt{2 \pi }} \int_{\gamma }^{+\infty}\left (e^{(1-\alpha)(\sqrt{\tau} \sigma z + y) -\frac{z^2}{2} } - x_s e^{-\alpha(y + \sqrt{\tau}\sigma z)-\frac{z^2}{2}} \right ) dz$

$U(y, \tau) =\frac{1}{\sqrt{2 \pi }}\left [ \int_{\gamma }^{+\infty}e^{(1-\alpha)(\sqrt{\tau} \sigma z + y)-\frac{z^2}{2}} dz -\int_{\gamma }^{+\infty} x_s e^{-\alpha(y + \sqrt{\tau}\sigma z)-\frac{z^2}{2}} dz \right ]$

, .

, , , , $e^{-\frac{v^2}{2}}$ , .

, $-\infty$ , . , . :

$\ frac {1} {\ sqrt {2 \ pi}} \ int _ {\ gamma} ^ {+ \ infty} e ^ {- \ frac {z ^ 2} {2}} dz = F (- \ gamma) \ qquad (*)$

, , . , , , . :

, $d_1 = - \ left (\ gamma - \ sigma \ sqrt {\ tau} (1- \ alpha) \ right)$ , $d_2 = - \ izquierda (\ gamma + \ alpha \ sigma \ sqrt {\ tau} \ derecha)$ , *.

, , . , :

$\ gamma = \ frac {\ ln x_s - y} {\ sigma \ sqrt {\ tau}}; \ qquad \ alpha = - \ frac {R} {\ sigma ^ 2}; \ qquad R = r - \ frac {\ sigma ^ 2} {2}; \ qquad y = \ ln x.$

$d_1 = \ frac {\ ln (xe ^ {r \ tau} / x_s)} {\ sigma \ sqrt {\ tau}} + \ frac {\ sigma \ sqrt {\ tau}} {2}; \ qquad d_2 = \ frac {\ ln (xe ^ {r \ tau} / x_s)} {\ sigma \ sqrt {\ tau}} - \ frac {\ sigma \ sqrt {\ tau}} {2}.$

, . $C (e ^ y, \ tau)$ , , $C (e ^ y, \ tau) = e ^ {\ alpha y + \ beta \ tau} \ cdot U (y, \ tau)$ , , ** $e ^ {\ alpha y + \ beta \ tau}$ .

. , $e ^ {\ alpha y + \ beta \ tau} \ cdot e ^ {y (1- \ alpha) + \ frac {1} {2} \ sigma ^ 2 \ tau (1- \ alpha) ^ 2}$ , $e ^ {\ alpha y + \ beta \ tau} \ cdot e ^ {{\ alpha y + a ^ 2 \ sigma ^ 2 \ tau / 2}}$ $e ^ {- r \ tau}$ . , :

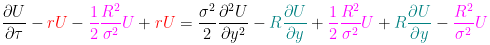
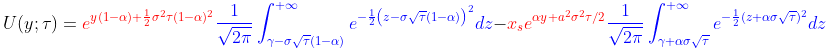
.. " ", 2009 . — 376 .
.. . 2, . 1985 . — 560 .
Wentzel E.S. L.A. Ovcharov Teoría de la probabilidad y sus aplicaciones de ingeniería. - M., ACADEMA, 2003.- 480 p.
Zhulenev S.V. "Matemáticas financieras. Introducción a la teoría clásica. Parte 2.", 2012 - 419 p.
Shiryaev A.N. "Fundamentos de las matemáticas financieras estocásticas. Volumen 1. Hechos. Modelos", 1998 - 512 p.

Opciones matemáticas o modelo Black-Scholes

Conceptos básicos

More articles: