🕘 🚠 📅 Cómo convertir texto a álgebra: ejemplos 🖖🏻 🧦 📗

En el artículo anterior , la representación de secuencias de signos mediante polinomios de unidades matriciales se desarrolló utilizando el ejemplo de un texto lingüístico. El texto se convierte en un objeto algebraico. Con el texto, puede realizar todas las operaciones algebraicas necesarias para la estructuración: cálculo de encabezados, diccionarios, anotaciones, marcado semántico. Este artículo proporciona dos ejemplos de la estructuración algebraica de textos de diferente naturaleza. Se eligió el código Morse debido a la extrema brevedad del diccionario y las fórmulas matemáticas como ejemplo de un problema inverso.

1. Código Morse-Weil-Gerke como álgebra de unidades matriciales

En código Morse, las secuencias de símbolos (textos) de 26 letras latinas consisten en puntos y guiones. El ejemplo se eligió debido a la extrema brevedad del diccionario ("punto" y "guión").

Las palabras aquí son puntos o guiones. 26 letras del alfabeto: textos de tales palabras. Cada palabra tiene dos coordenadas. La primera coordenada es el número de la palabra (punto o guión) en esta letra (de uno a cuatro). La segunda coordenada es el número en el diccionario (1 o 2). Diccionario E ₁₁ ("punto") y E ₂₂ ("guión").

$D_R = E_ {11} + E_ {22}$

Tabla 1. Código Morse: letras latinas como secuencias de signos (textos)

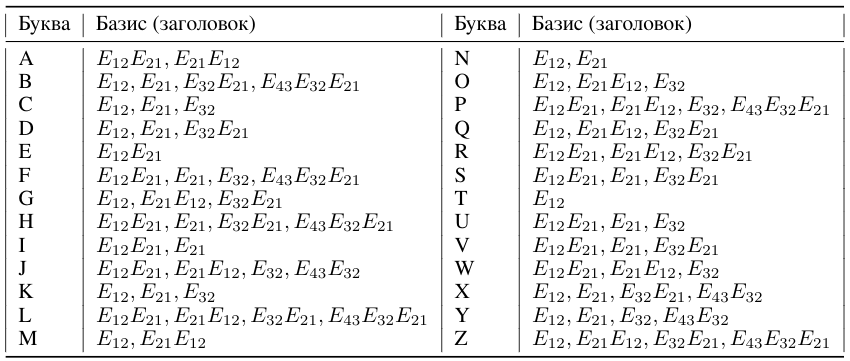
Cada letra (secuencia de signos) con un número de la Tabla 1 se puede asociar con un polinomio matricial P de 4x4 unidades matriciales de acuerdo con la fórmula (8) del artículo [1] .

Tabla 2: Código Morse: letras como polinomios matriciales

Por ejemplo, la letra Q (No. 17) está asociada con un polinomio matricial:

$E_ {12} + E_ {22} + E_ {31} + E_ {42} = \ begin {Vmatrix} 0 & 1 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \ end {Vmatrix}.$

26 - 2 , E₁₂, E_21, E₃₂

26 2 ||P||, , :

$\begin{Vmatrix} a_{11} & \ldots & a_{1n}\\ \ldots & \ldots & \ldots\\ a_{m1} & \ldots & a_{mn} \end{Vmatrix} \begin{Vmatrix} b_{1} \\ \ldots \\ b_{n} \end{Vmatrix}= \begin{Vmatrix} a_{11} \\ \ldots \\ a_{m1} \end{Vmatrix}b_1+\ldots + \begin{Vmatrix} a_{1n} \\ \ldots \\ a_{mn} \end{Vmatrix}b_n,$

2 ||P||₁, ||P||₂, ||P||₃.

$\left\|P\right\|_1=\begin{Vmatrix} E_{12} \\ E_{21} \\ E_{32} \end{Vmatrix}, \left\|P\right\|_2=\begin{Vmatrix} E_{12} \\ E_{21}E_{12} \\ E_{12}+E_{21}E_{12} \\ E_{12}E_{21} \\ E_{21} \\ E_{21}+E_{12}E_{21} \\ E_{32} E_{21} + E_{43}E_{32} E_{21} \\ E_{43}E_{32} E_{21} \\ E_{32} E_{21} \\ E_{32} \\ E_{32} + E_{43}E_{32} \\ E_{43}E_{32} \end{Vmatrix}, \left\|P\right\|_3=\begin{Vmatrix} E_{12}E_{21} \\ E_{12} \\ E_{21} \\ E_{21}E_{12} \\ E_{32}E_{21} \\ E_{32} \\ E_{43}E_{32} E_{21} \\ E_{43}E_{32} \end{Vmatrix}, (1.1)$

||P||₂(||P||₂)^T - - – ( ), , – () - .

(||P||₂)^T||P||₂ - - – , , – – () .

() (1.3). (1.3). 3 4:

: ABCDEFGHIJKLMNOPQRSTUVWXYZ

- ( - E₁₂, E_21, E₃₂) ( ) E₁₂, E_21, E₃₂:

E₁₂ - , «» 4- :

_BCD__G___K_MNO_Q__T___XYZ (13 )

E₂₁ - , «» 4- :

_BCD_F_HI_K__N____S_UV_XY_ (13 )

E₃₂ - , «» 4- :

__C__F___JK ___OP____U_W_Y_ (9)

2.

[1] ( ), . – () ( ), , , . .

V_K, V V:

$V_K=\frac{1}{3}\pi R_1^2H_1, V_{\text{}}=\pi R_2^2H_2, V_T=\pi^2\left(R_3+R_4\right)r,\ \ \ \ \ \ \ \ \ (2.1)$

. , . , R₁² – R₁R₁, πR₁ – , . (1): R₁ H₁ – , R₂ H₂ – , R₃ – , R₄ – , r – , π – π.

. . (2.1) , π. R₁, R₂, R₃, R₄, H₁, H₂ r – . , , ( ), – : R₁=ar, R₂=br, R₃=cr, R₄=dr, H₁=er, H₂=fr . (2.1):

$\begin{gathered} \frac{1}{3}\pi ararer \\ \pi brbrfr \\ \pi \pi \left(c+d \right)rr \end{gathered} \ \ \ \ \ \ \ \ \ \ \ \ (2.2)$

$\begin{gathered} \left(\frac{1}{3}\right)_{1,1}(\pi)_{2,2}(a)_{3,3} (r)_{4,4} (a)_{5,3} (r)_{6,4} (e)_{7,7} (r)_{8,4} \\ (\pi)_{9,2} (b)_{10,10} (r)_{11,4} (b)_{12,10} (r)_{13,4} (f)_{14,14} (r)_{15,4} \\ (\pi)_{16,2} (\pi)_{17,2} \left(c+d \right)_{18,18} (r)_{19,4}(r)_{20,4} \end{gathered} \ \ \ \ \ \ \ \ \ (2.3)$

(2.2)

$P=F_1(P)+F_2(P)+F_3(P), \ \ \ \ \ \ \ \ \ \ (2.4)$

$\begin{gathered} F_1(P) = D_L\left(E_{1,1}+E_{2,2}+E_{3,3}+E_{4,4}+E_{5,3}+E_{6,4}+E_{7,7}+E_{8,4}\right)D_R \\ F_2(P) = D_L\left(E_{9,2}+E_{10,10}+E_{11,4}+E_{12,10}+E_{13,4}+E_{14,14}+E_{15,4}\right) D_R \\ F_3(P) = D_L\left(E_{16,2}+E_{17,2}+E_{18,18}+E_{19,4}+E_{20,4}\right) D_R \\ D_R = E_{1,1}+E_{2,2}+E_{3,3}+E_{4,4}+E_{7,7}+E_{10,10}+E_{14,14}+E_{18,18} \\ D_L = E_{1,1}+E_{2,2}+E_{3,3}+E_{4,4}+E_{5,5}+E_{6,6}+E_{7,7}+ \ldots + E_{20,20} = E \\ D_L=D_R+E_{5,5}+E_{6,6}+E_{5,5}+E_{8,8}+E_{5,5}+E_{9,9} \end{gathered}$

- :

P (2.1) . , , . , «1/3» ( E_1,1), «a» ( E_3,3+E_5,3) , «e» ( E_7,7) ( (2.5)). ( (2.5)) «b» ( E_11,11+E_13,11) «f» ( E_15,15). ( (2.5)) (c+d) ( E_20,20). , (2.5). :

$\begin{gathered} P = P_{\text{}_1}P_{\text{}_1}+P_{\text{}} \\ P = P_{\text{}_2}P_{\text{}_1}+P_{\text{}} \end{gathered}$

$\begin{gathered} P_{\text{}_1} = \left(E_{2,18}+E_{4,12}+E_{6,14}+E_{8,16}\right) +\left(E_{10,18}+E_{12,12}+E_{14,4}+E_{16,16}\right)+\\ +\left(E_{18,18}+E_{19,19}+E_{21,12}+E_{22,14}\right), \\ P_{\text{}_2} = (E_{2,2}+E_{4,4}+E_{6,4}+E_{8,4})+(E_{10,2}+E_{12,4}+E_{14,4}+E_{16,4})+ \\ +(E_{18,2}+E_{19,2}+E_{21,4}+E_{22,4}), \\ P_{\text{}_1} = E_{18,2} + E_{19,2}+E_{12,4} + E_{14,4} + E_{16,4}, \\ P_{\text{}_2} = E_{2,2} + E_{4,4}, \\ P_{\text{}} = E_{1,1}+E_{3,3} + E_{5,3}+E_{7,7}+E_{11,11} + E_{13,11}+E_{15,15}+E_{20,20}.\\ \end{gathered}$

(2.6) P₁ P₂. P₁ (2.1). P₂ D_R (2.1). , (, – , , , ). , , π r^₂, r^₂π.

- (2.6):

$\begin{gathered} P_{\text{}_1}+P_{\text{}} \\ P_{\text{}_2}+P_{\text{}} \end{gathered}$

$\ begin {collect} P = P _ {\ text {privado} _1} \ left (P _ {\ text {div} _1} + P _ {\ text {rest}} \ right) \\ P = P _ { \ text {privado} _2} \ left (P _ {\ text {div} _2} + P _ {\ text {rest}} \ right) \ end {reunido}$

P₁ P₂ ( ). . , - P₁ P₂ , .

. . . . . , (2.3) :

P₁ P₂ ( π r ),
P₁ P₂ (),
π r P₁ P₂(1,1,2 3,3,2),
P₁ P₂,
P (, -).

[1] Pshenichnikov S.B. Álgebra de texto. Researchgate Preprint, 2021

Cómo convertir texto a álgebra: ejemplos

1. Código Morse-Weil-Gerke como álgebra de unidades matriciales

2.

More articles: