Historia
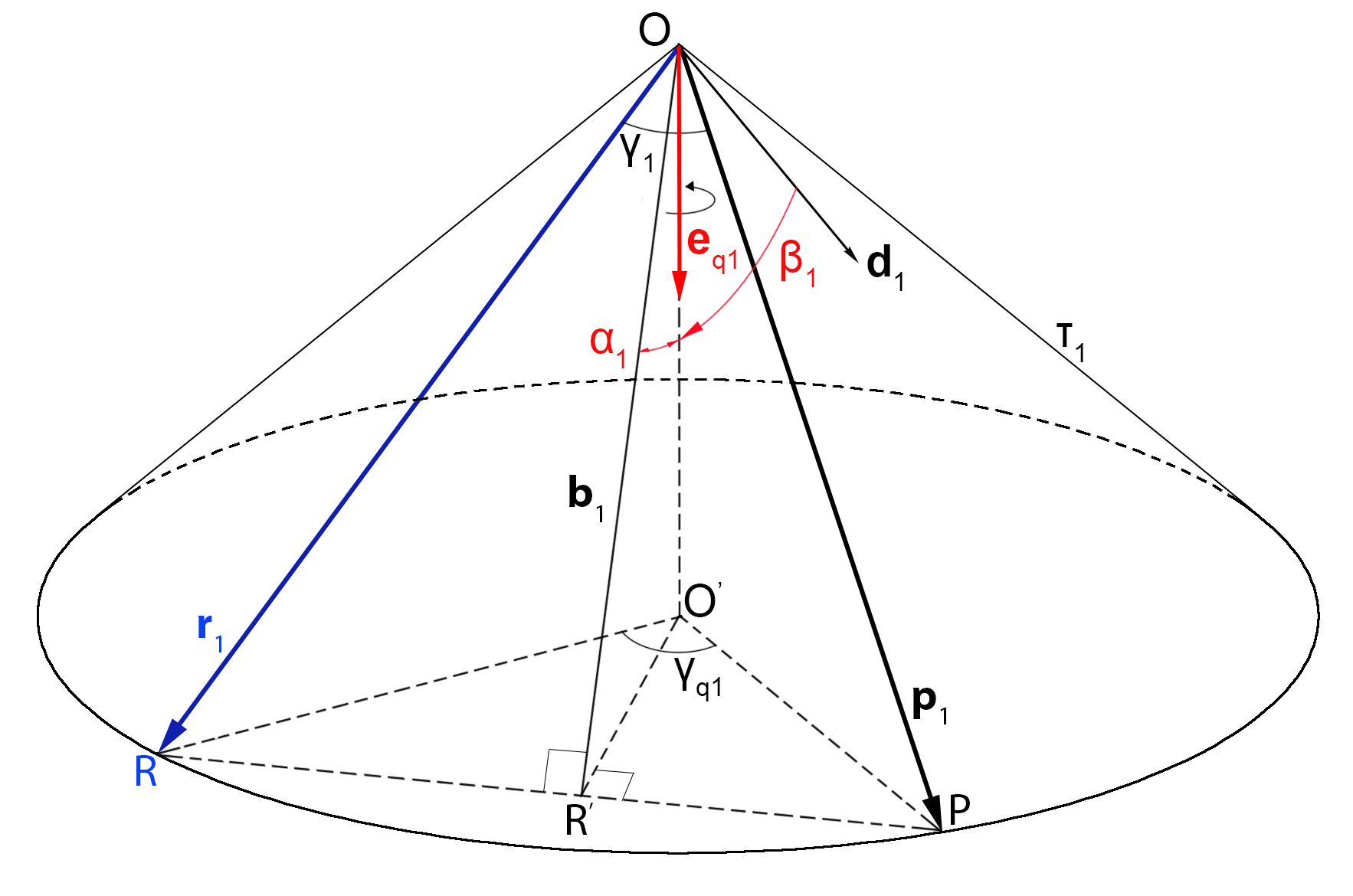
Hace algún tiempo me enfrenté a un problema interesante relacionado con la navegación por satélite. Usando el frente de fase de la señal, el objeto de navegación (NVO) mide las coordenadas de los satélites de navegación (NS) en su sistema de coordenadas (sistema local, LSK). Además, el ONV recibe los valores de las posiciones del NS en el sistema de coordenadas global (GCS), y mide el tiempo de recepción de la señal del NS (Fig. 1). Se requería calcular las coordenadas de la ONV en el GSK y la hora del sistema, es decir, solucionar el problema de navegación.
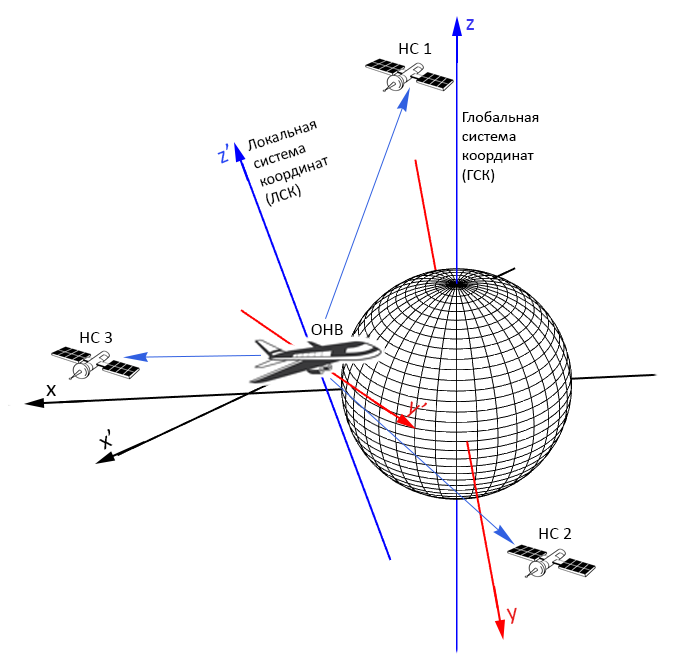
El problema era interesante porque su solución teóricamente permite reducir el número de NN en comparación con el número de NN que se requieren en los métodos implementados en los sistemas de navegación por satélite. En ese momento, me dediqué principalmente al estudio de la calidad de las mediciones del frente de fase y la obtención de ecuaciones de navegación para coordenadas y tiempo, asumiendo que el cálculo de la orientación y coordenadas del NVG no causaría ningún problema especial. Además, en un avión, el problema se resolvió rápida y fácilmente.
, , , . , . - , .
, , . , . , , , .
, :
: -
- ,
: ,
: -
- ;
; , : 3-
; . , - , , .
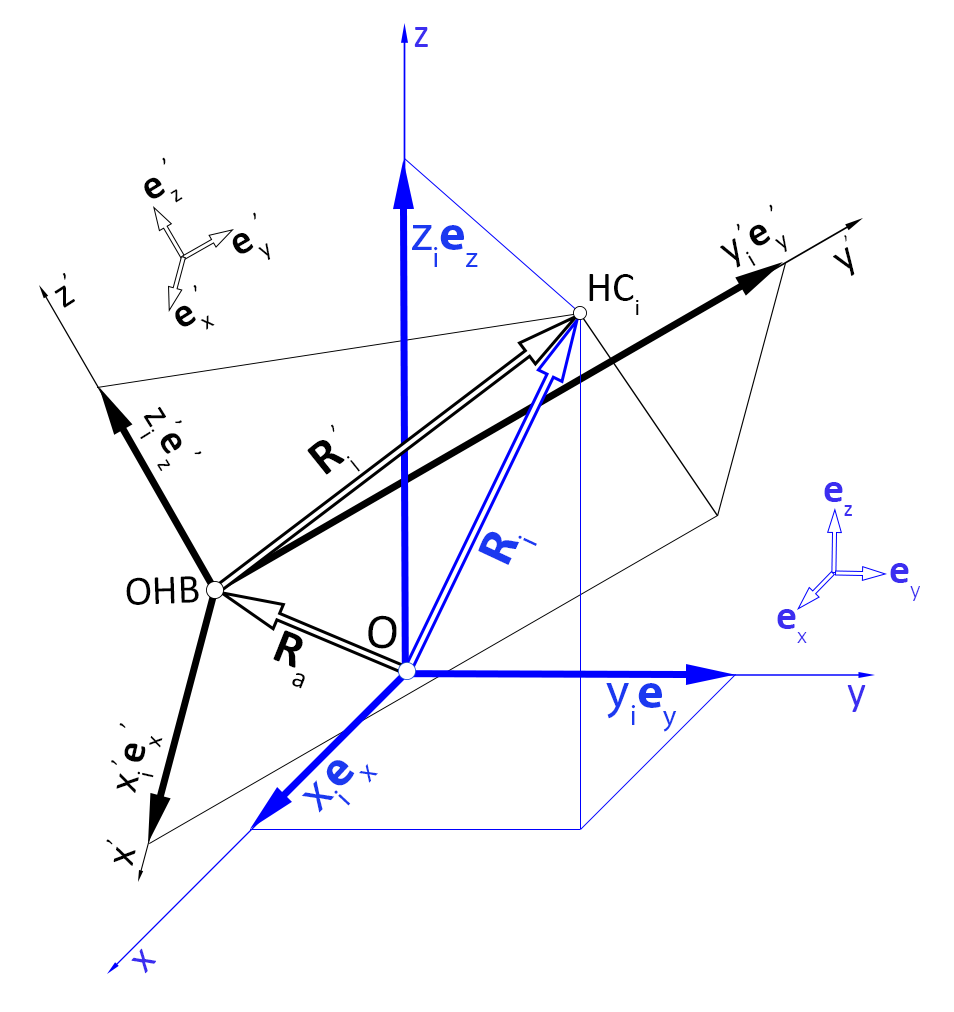
:
: - ,
: , " " (. 2)
.
:
,
- .
,
- ,
.
, ,
,
. ,
. ,
( " "), ,
, . .
:
(1)
(1)
, .
,
. (1) (2) ,
:
.
- (3) (1), . , (3) (2), .
, .
, , (3) (4) . , .
, , , .
, , ,
,
,
,
,
- ( ),
- ; 1, i, j, k - :
(), , . , ,
, ,
,
,
,
. , - .
,
,
,
:
.
,
,
,
,
. "
", , ,
(5).
. :
: ,
: ,
: .
.
. , . k = 1 , i = 2.
-, , , .
-, . , , (3) .
, -, . ,
- ,
, (3) ,
.
T (3) ,
:
:
(3) :
- ,
, (1) :
,
.
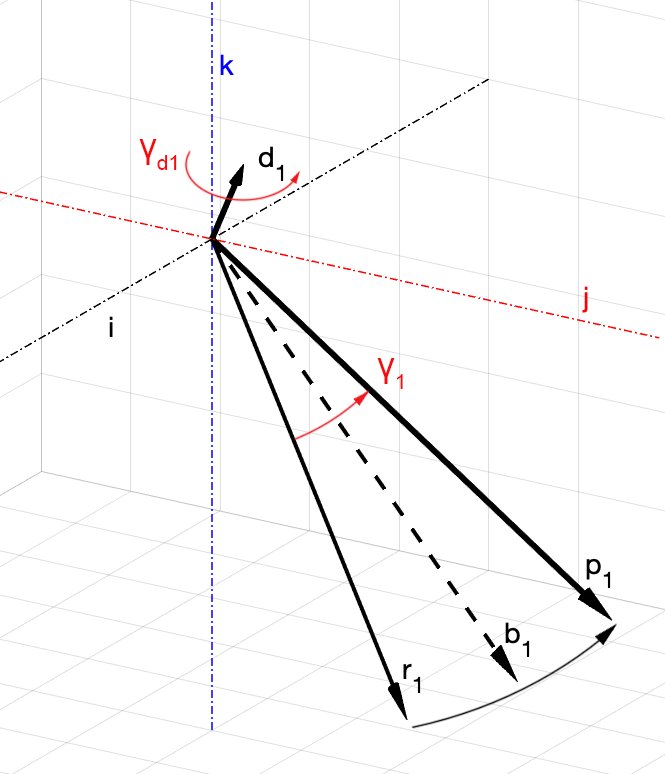
, , ,
, (
). ,
(. 3), ,
.
(6), (3), - : , (6). , , ,
. . 3 ,
,
. ,
.
. 4, ) ) ,
. , ,
, (
),
,
,
,
.
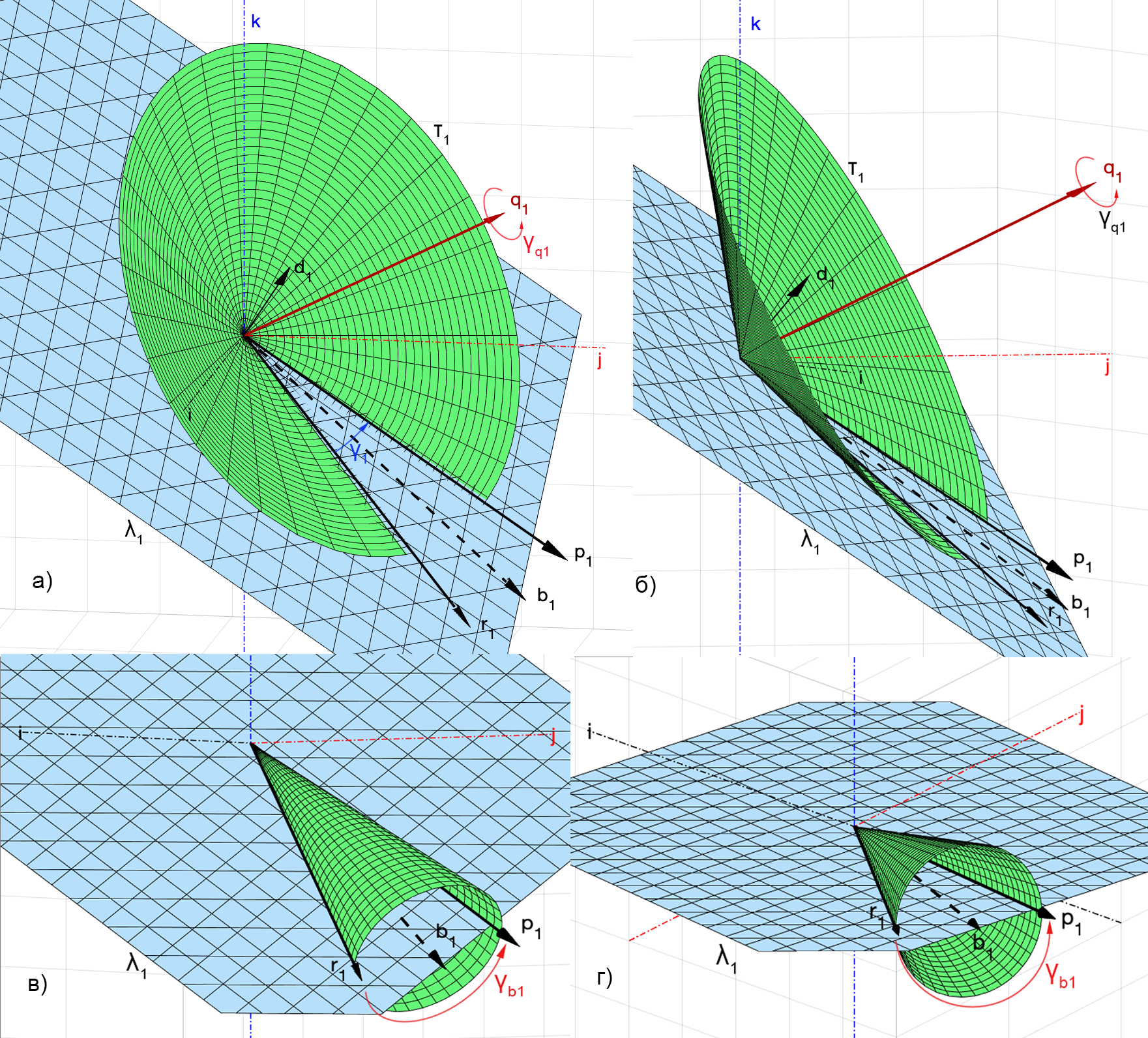
,
,
. (6), (4),
, , (8), , , . , (7)
- .
(8), - , , - .
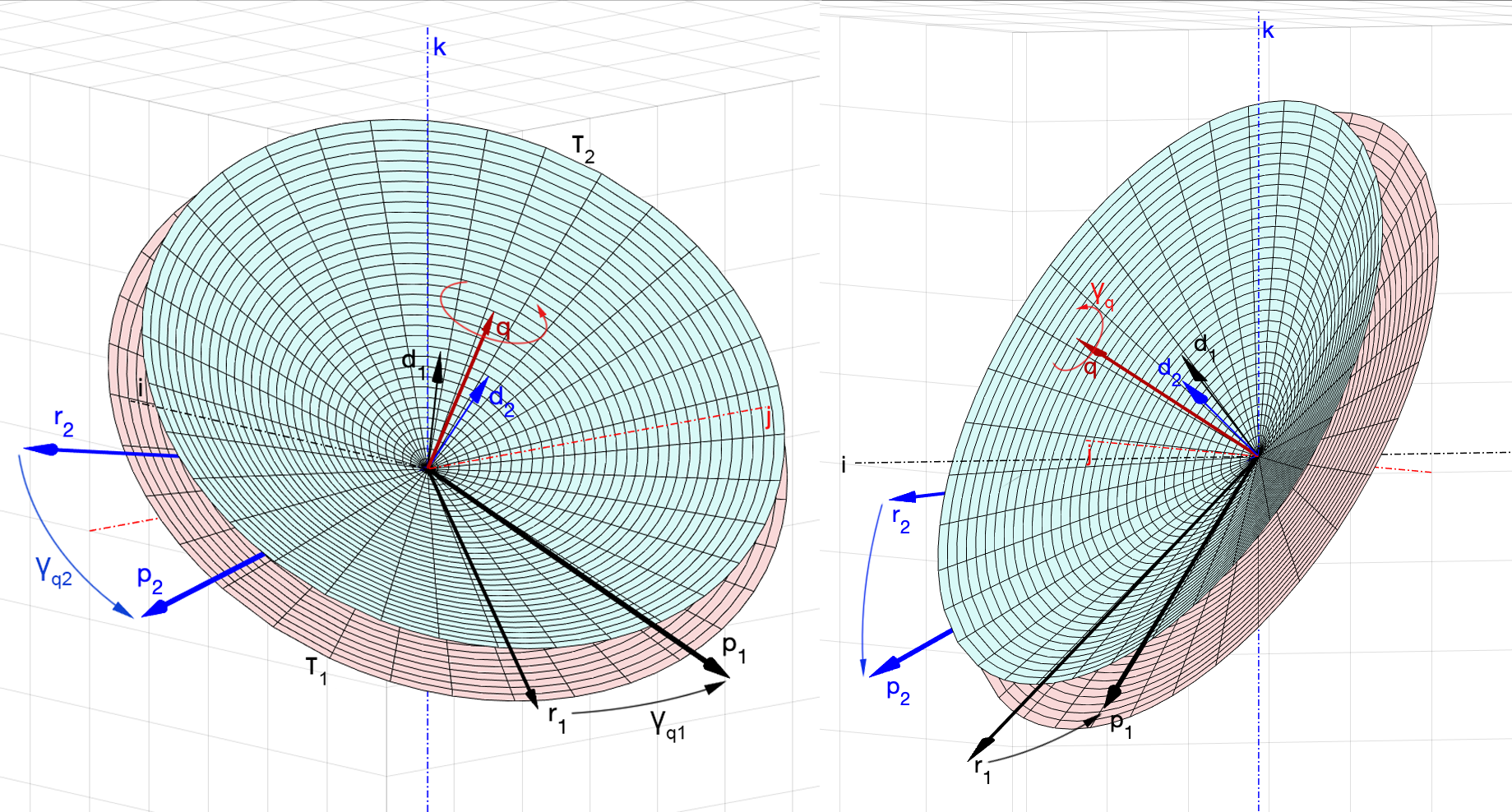
. , ,
,
. ,
(
)
(
),
,
. ,
.
, i = 1, 2, ,
,
,
(. 5).
.
1. ,
,
(. 4, ), )).
2. ,
, i = 1, 2, , ,
(
), . 6). .
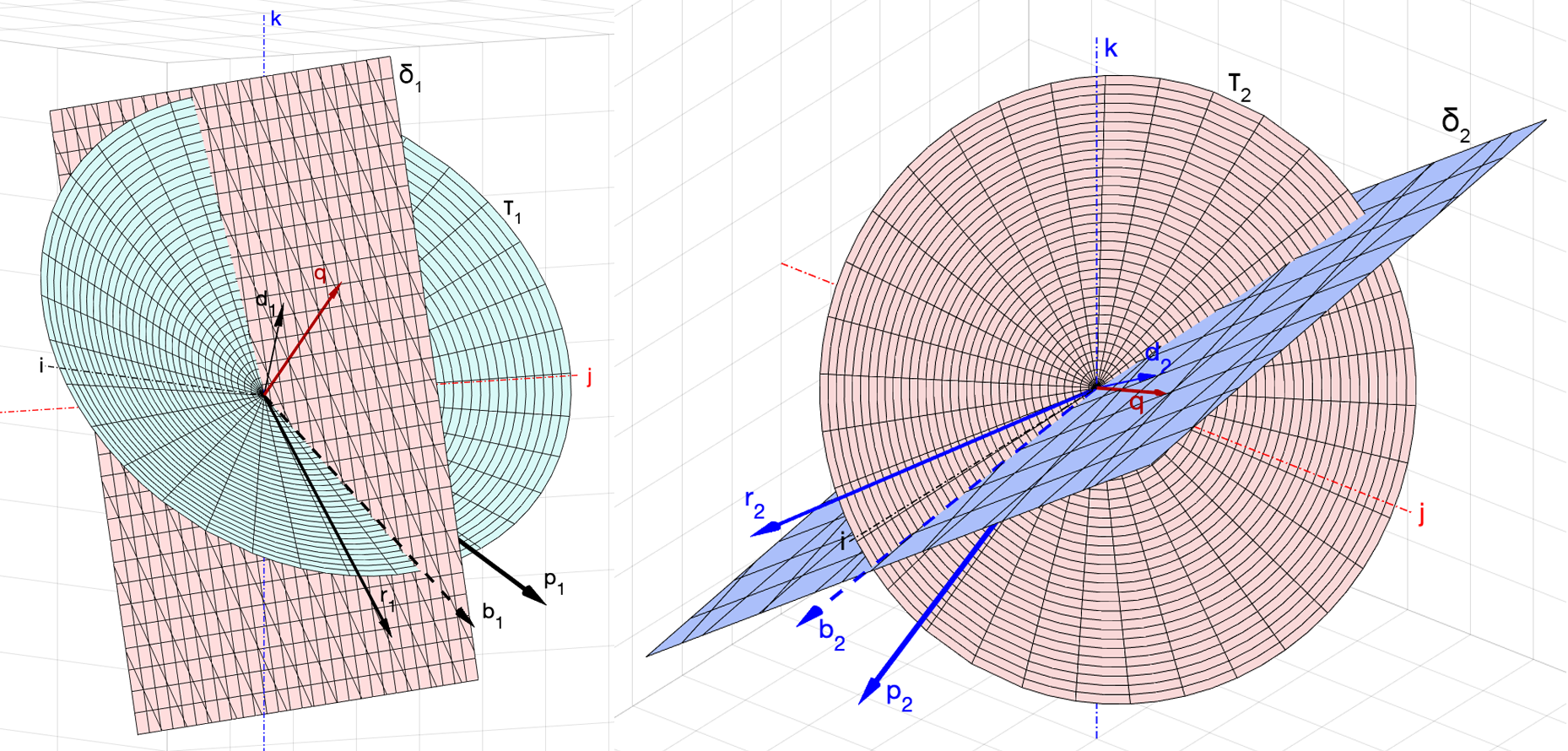
, ,
(
),
.
, , ,
, i = 1, 2,
, .
(. 7).
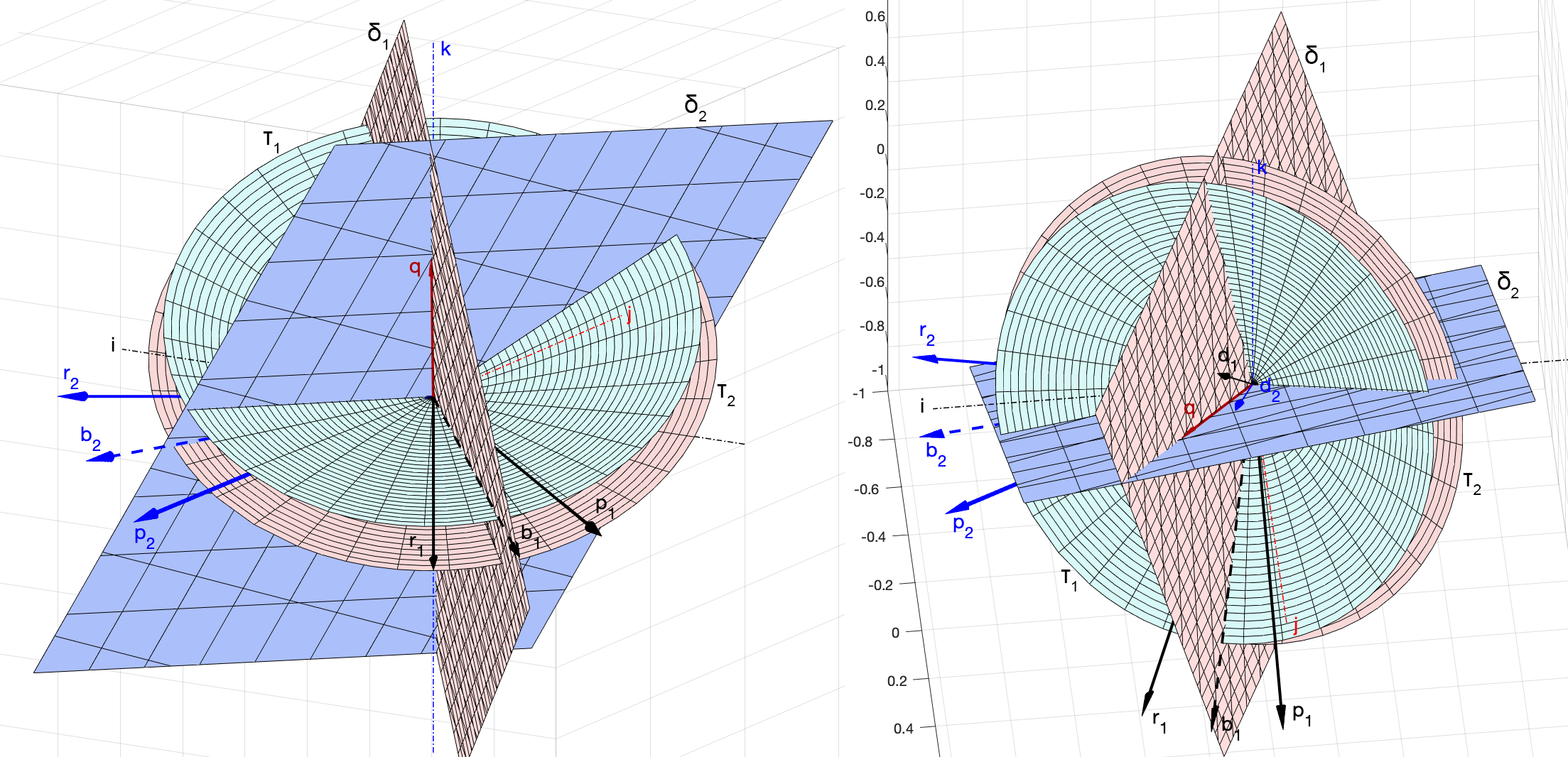
, . ,
,
(. 8).
.
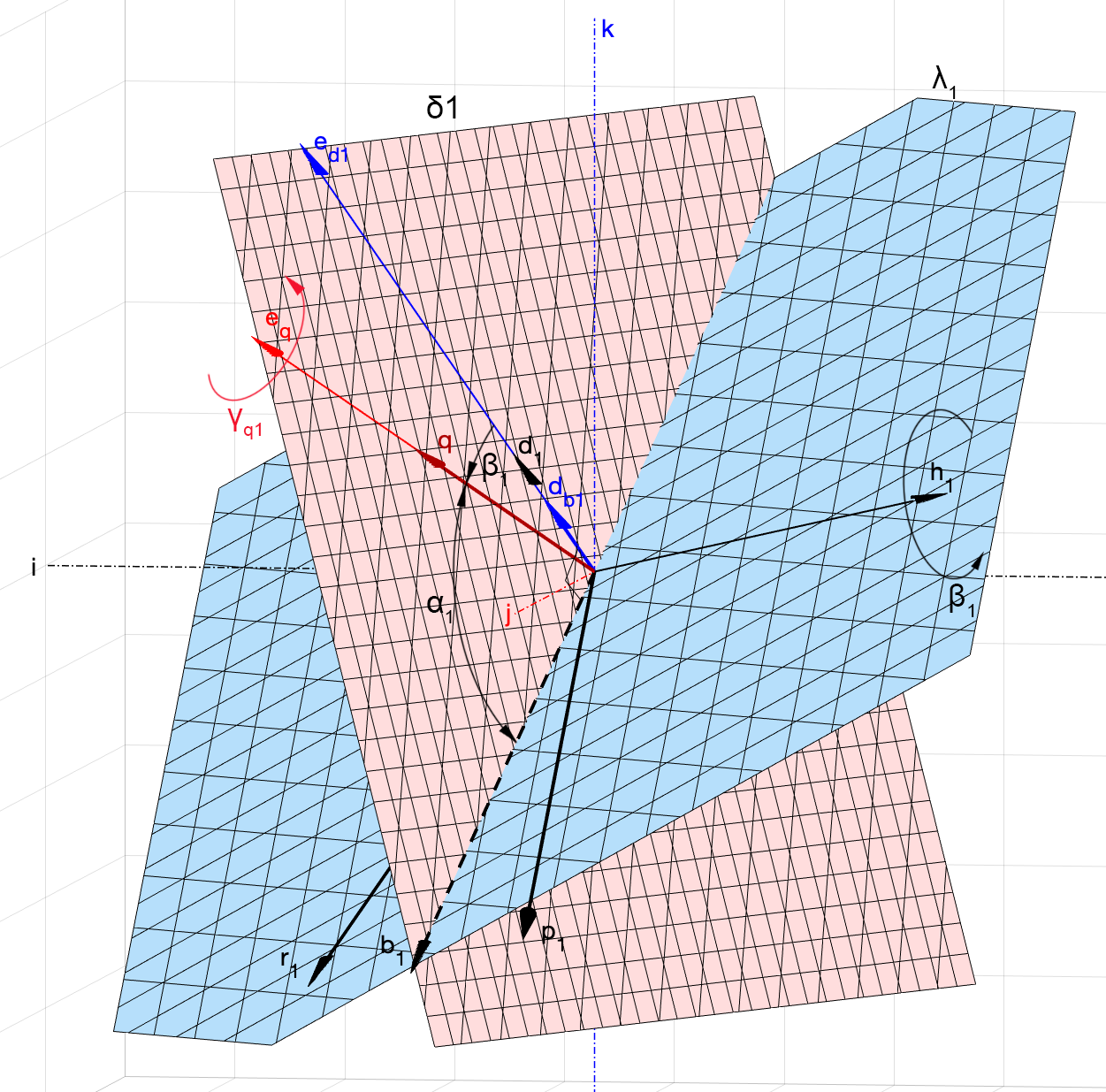
. 8. ,
, ..
,
,
,
.
,
.
2 ,
, , ,
. ,
,
, .
.
.
,
.
: . ,
,
.
, ,
. ,
, ,
, . ,
,
,
:
, . , ,
,
,
,
,
. "1" "2" " i ", , i = 1, 2 .
,
, :
:
,
:
;
,
,
:
;
1,
:
;
,
:
,
:
;
,
:
,
, ,
:
,
.
,
.
,
(. 3).
.
,
, :
- ,
,
:
.
.
- ,
. (17),
(19) (18), , (14), :
" " ,
, .
.
. 6, (. 9).
.
,
,
,
,
(..
). ,
.
:
.
),
(21) ,
,
, 1. ,
,
.
. .
,
, ,
. (9), (18), ,
, (22),
.
. (9),
. :
. (23) (9), :
,
,
. , :
.
. ,
,
( (11)),
. ,
,
,
. (23)
, :
,
(12) , :
, :
,
(24), (13) :
(29).
. (30), . , , . . 10 , .
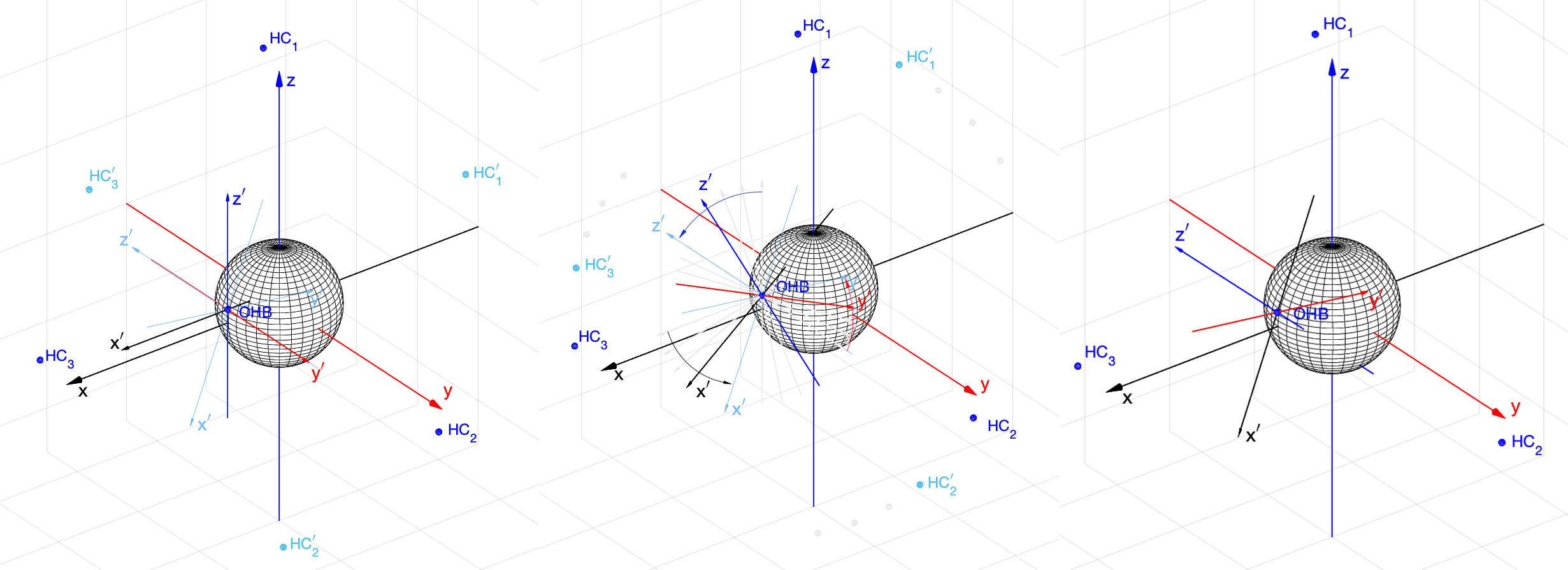
, , , , ( , "", , ). 1', 2' 3' 1, 2 3 (. 10, )). ,
(30) . . 10, ) 10 . ( - ) . . 10, ) ,
, (, , ).
Eso es todo por ahora. Solo señalaré que en un futuro próximo intentaré trabajar en un inconveniente de la expresión (30). Cuando está cerca de cero, es decir, cuando las orientaciones del HSC y LSC difieren poco, el cuaternión se
calcula con un error debido al multiplicador
. Esto puede provocar errores importantes en el cálculo de la orientación del LCS y, como resultado, errores en la determinación de la posición
. Más sobre esto en el próximo artículo.