Formulación del problema
Muchos han oído hablar de la curva ROC, que se usa a menudo en ML . Al decodificar esta abreviatura, obtenemos esa ROC ( característica operativa del receptor ). Traducido del inglés, esto significa RHP ( rendimiento del receptor ). Este concepto está tomado de la teoría de la detección de señales. La curva ROC se puede asociar a una estación de radar ( radar ), considerándola desde el punto de vista de la detección de objetos. Describamos esto de manera más formal.
El radar envía pulsos que rebotan en los objetos. La señal reflejada es recibida por la antena receptora del radar ( Fig. 1 ). Si hay algún objeto ubicado en la zona de detección ( DZ )
, entonces la señal reflejada será más alta que el umbral de detección
y esto significará la presencia del objeto
. Si la señal reflejada está por debajo del umbral de detección, esto significa que no hay ningún objeto
.

ZO
La zona de detección de radar es el área del espacio dentro de la cual el radar asegura la detección de objetos con probabilidades de detección correcta no peores que las requeridas.
,
.
— . ,
, .
, , ,
. ,
, - , :
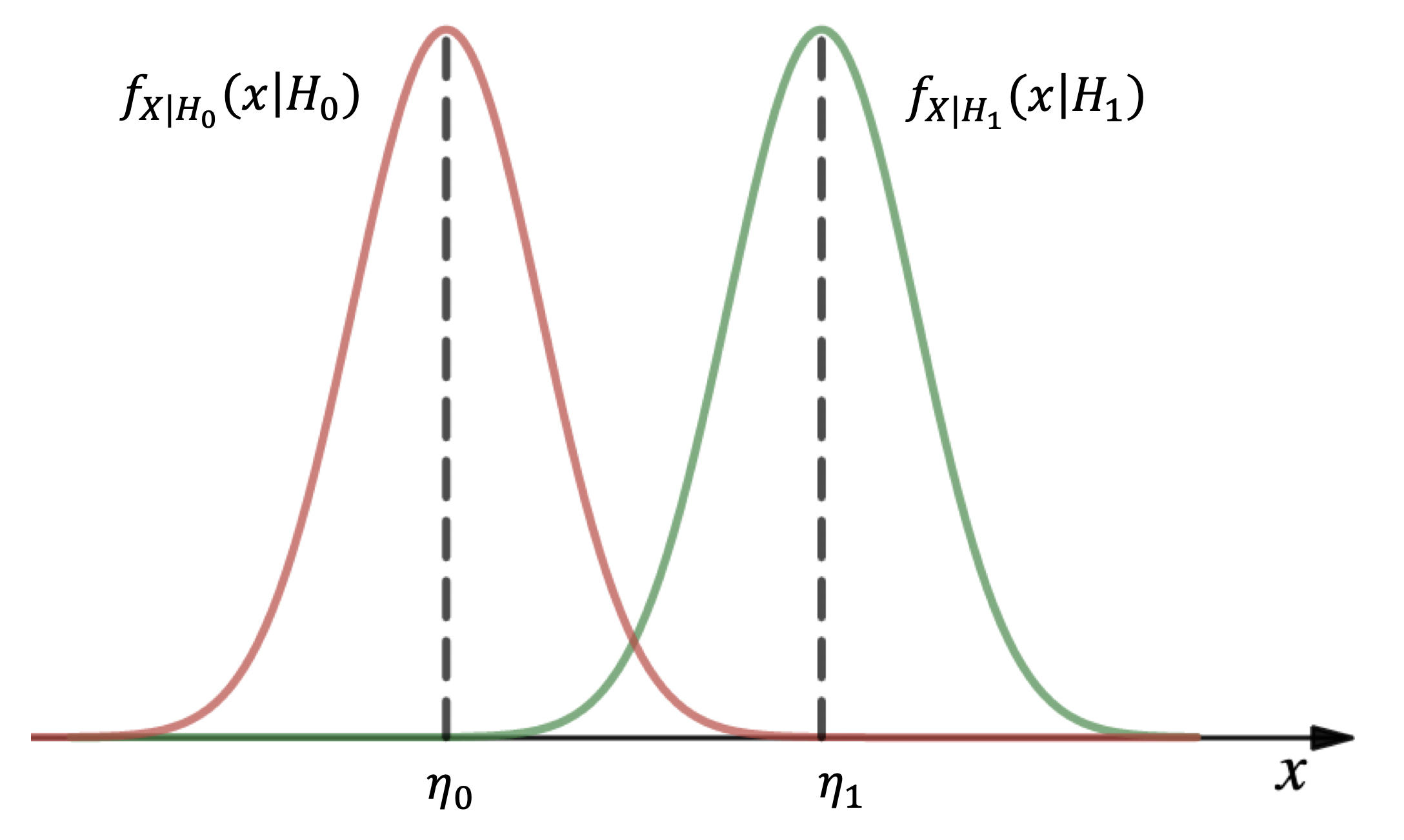
. 2 —
. ,
, ,
.
, ,
.
. . 2
, :
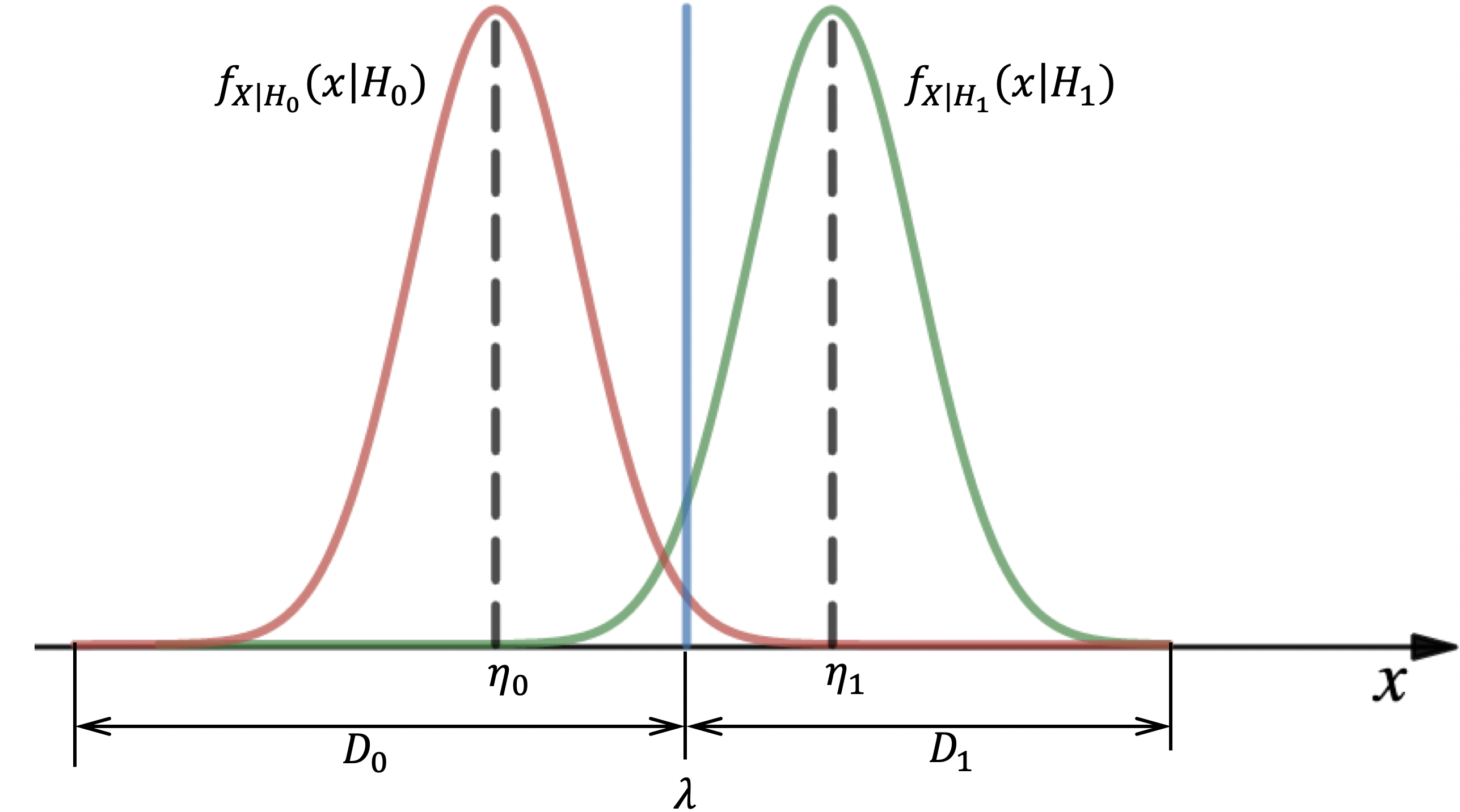
:
:
– ,
, .. .
– , ..
, ,
, .. .
, :
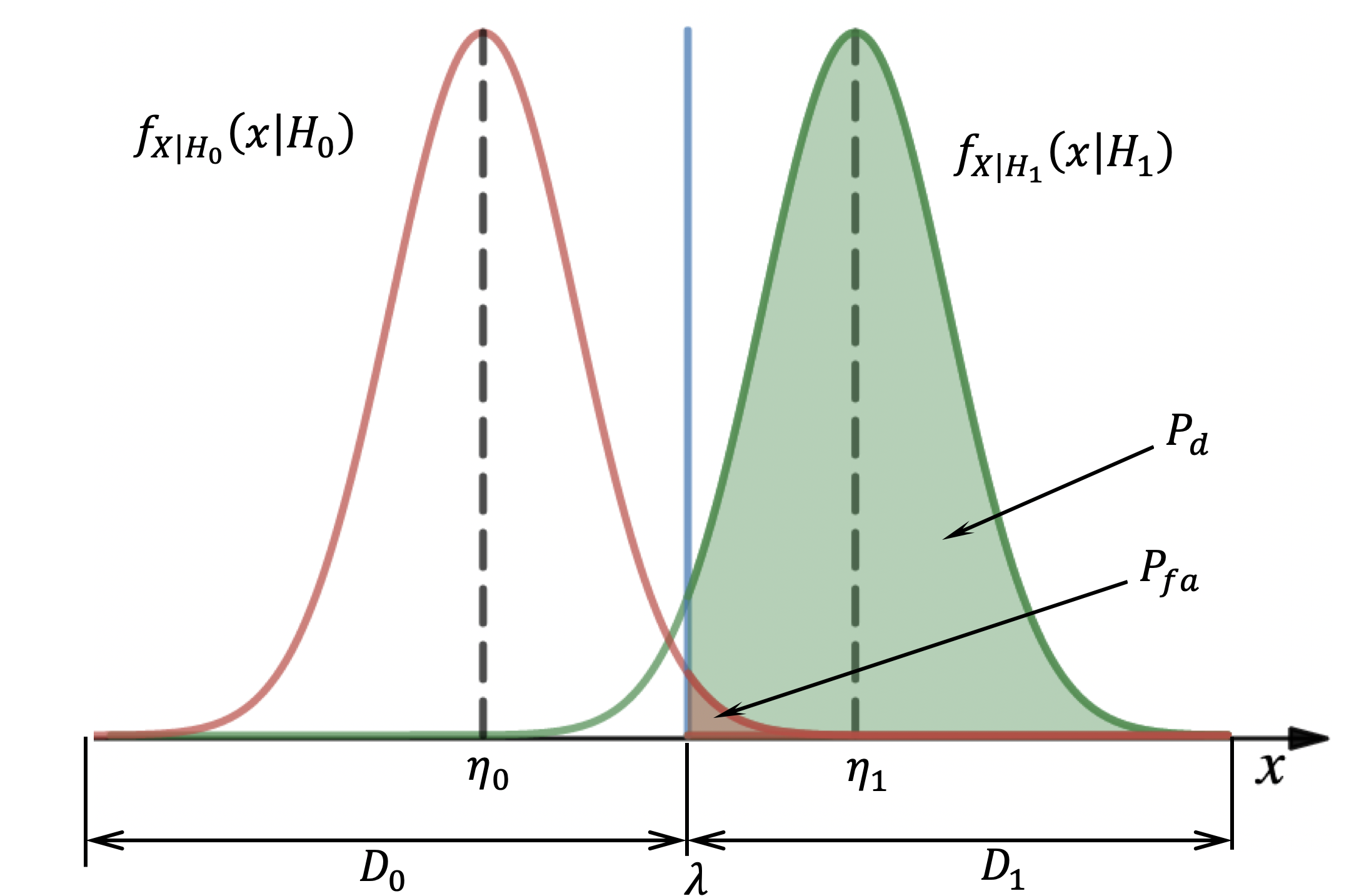
, , ,
.
,
, ROC- (. Receiver Operating Characteristic, ).
- (, . Signal-to-Noise Ratio, .
), :
– ;
– .
,
– , :
ROC-
:
, , , ..
,
–
.
.
, ,
,
.
,
.
:
, :
ROC- :
, ..
. ROC-
,
.
, :
– ROC- ROC-.
:
, ..
.
, ..
. , .
ROC-.
Python.
#
from scipy.stats import norm
from scipy.misc import derivative
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns; sns.set()
%matplotlib inline
# SNR lambda
SNR_values = np.arange(-1, 5.5, 1/2)
lambda_values = np.arange(0, 1.01, 1/100)
# , sigma SNR
def snr_to_sigma(SNR):
return np.power(10, -SNR/20)
# , Pfa Pd sigma lambda
def roc_curve(sigma, lambda_):
return 1 - norm.cdf(lambda_/sigma), 1 - norm.cdf((lambda_ - 1)/sigma)
# DataFrame Pfa, Pd, SNR
data = []
for SNR in SNR_values:
for lambda_ in lambda_values:
Pfa, Pd = roc_curve(snr_to_sigma(SNR), lambda_)
data.append([Pfa, Pd, str(SNR)])
data = pd.DataFrame(data, columns=['Pfa', 'Pd', 'SNR'])
fig, ax = plt.subplots(figsize=(18, 14))
sns.set_context('poster')
plt.title('$ROC$- $SNR$', fontsize=40)
plt.xlabel('$P_{fa}$', fontsize=40)
plt.xticks(np.arange(0, 0.7, 0.05), fontsize=30)
plt.yticks(np.arange(0.5, 1, 0.05), fontsize=30)
plt.ylabel('$P_d$', fontsize=40, rotation=0, labelpad=40)
sns.lineplot(x='Pfa', y='Pd', hue='SNR',
data=data, palette='gist_ncar', ax=ax)
ax.annotate(" $\lambda$", xy=(0.15, 0.81), xycoords='data',
xytext=(90, 150), textcoords='offset points',
size=30, ha='left',
arrowprops=dict(arrowstyle="->", color='black',
connectionstyle="arc3,rad=0.1"))
plt.grid(color='black', linestyle='--', linewidth=1, alpha=0.3)
plt.legend(fontsize='small', shadow=True, title='$SNR(dB)$',
borderpad=0.9, fancybox=True);
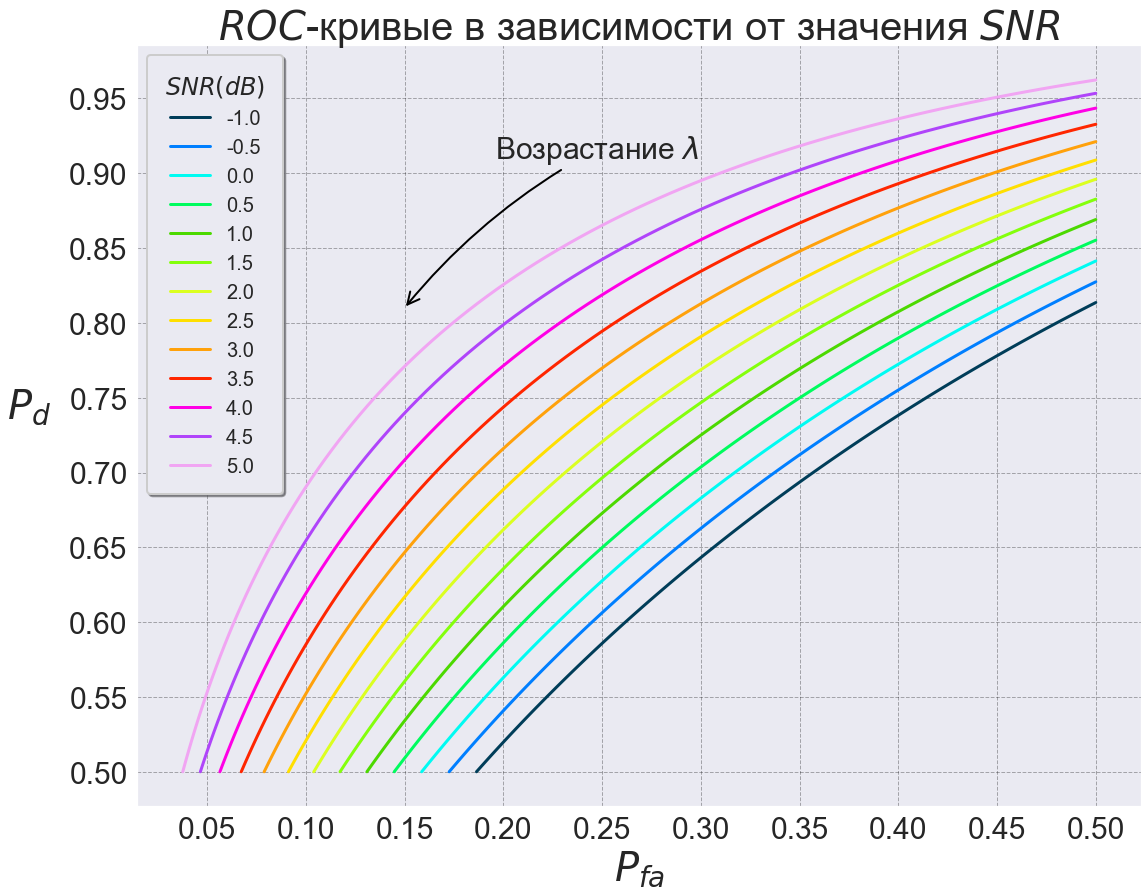
:
;
, ROC-
;
;
ROC - . , .
. , ROC-,
, ,
.
# DataFrame Pfa, Pd, SNR
data2 = []
for SNR in SNR_values:
for lambda_ in np.arange(-10, 10.1, 1/10) :
Pfa, Pd = roc_curve(snr_to_sigma(SNR), lambda_)
data2.append([Pfa, Pd, str(SNR)])
data2 = pd.DataFrame(data2, columns=['Pfa', 'Pd', 'SNR'])
fig, ax = plt.subplots(figsize=(18, 14))
sns.set_context('poster')
plt.title('$ROC$- $SNR$', fontsize=40)
plt.xlabel('$P_{fa}$', fontsize=40)
plt.xticks(np.arange(0, 1.05, 0.1), fontsize=20)
plt.yticks(np.arange(0, 1.05, 0.1), fontsize=20)
plt.ylabel('$P_d$', fontsize=40, rotation=0, labelpad=40)
sns.lineplot(x='Pfa', y='Pd', hue='SNR',
data=data2, palette='gist_ncar', ax=ax)
ax.annotate(" $\lambda$", xy=(0.15, 0.81), xycoords='data',
xytext=(90, 110), textcoords='offset points',
size=20, ha='left',
arrowprops=dict(arrowstyle="->", color='black',
connectionstyle="arc3,rad=0.1"))
plt.grid(color='black', linestyle='--', linewidth=1, alpha=0.3)
plt.legend(fontsize='small', shadow=True, title='$SNR(dB)$',
borderpad=0.9, fancybox=True);
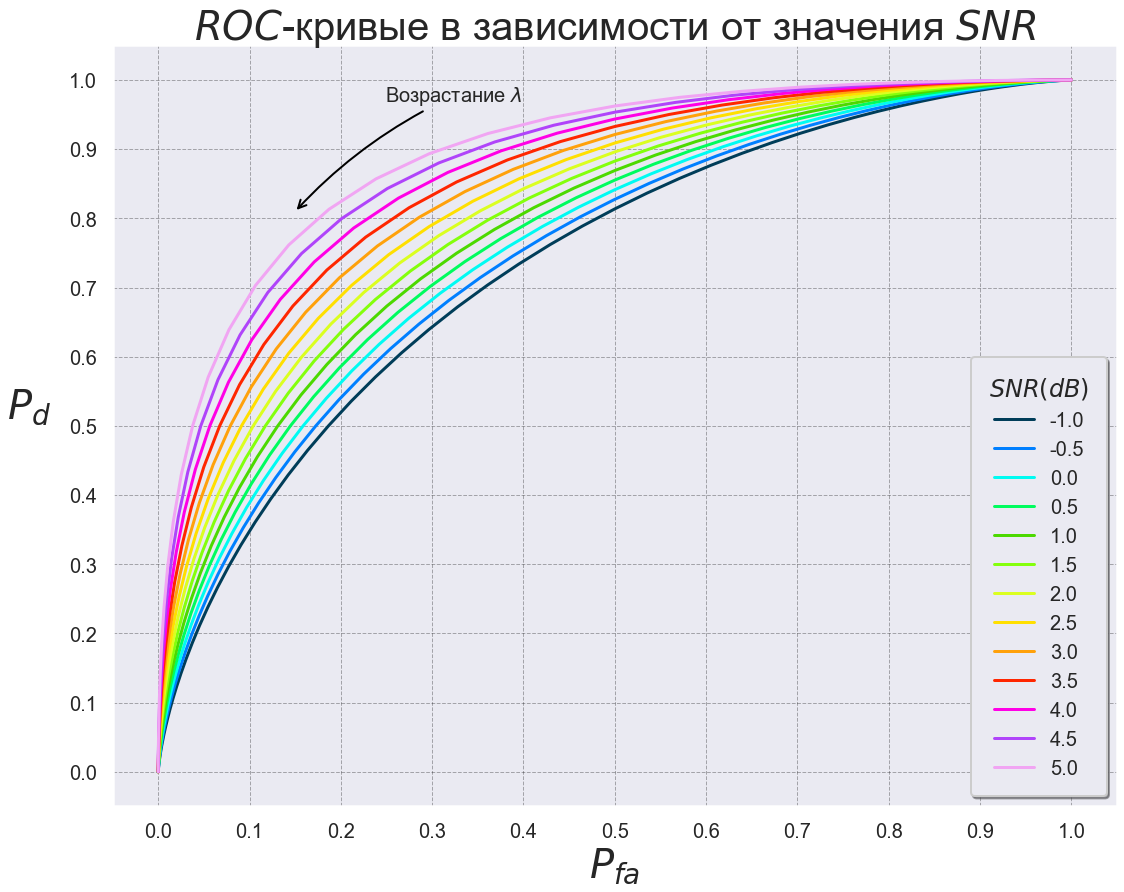
,
. ,
,
,
. ,
.
# , sigma
def conditional_density(x, sigma):
return norm.pdf(x/sigma), norm.pdf((x - 1)/sigma)
# DataFrame SNR
data3 = []
x_range = np.linspace(-5, 5, 100)
for SNR in SNR_values:
for x in x_range :
cond_dens1, cond_dens2 = conditional_density(x, snr_to_sigma(SNR))
data3.append([cond_dens1, cond_dens2, str(SNR), x])
data3 = pd.DataFrame(data3, columns=['cond_dens1', 'cond_dens2', 'SNR', 'x'])
fig, ax = plt.subplots(figsize=(20, 10))
sns.set_context('poster')
plt.title(' $SNR$',
fontsize=30)
plt.xlabel('$x$', fontsize=40)
plt.xticks(np.arange(-5, 5.5, 0.5), fontsize=20)
plt.yticks(np.arange(0, 0.45, 0.05), fontsize=20)
plt.ylabel(' ', fontsize=20,
labelpad=30)
sns.lineplot(x='x', y='cond_dens2', hue='SNR',
data=data3, palette='gist_ncar', ax=ax)
sns.lineplot(x='x', y='cond_dens1', hue='SNR',
data=data3, palette='gist_ncar', ax=ax, legend=False)
ax.legend(fontsize='small', shadow=True, title='$SNR(dB)$',
borderpad=0.9, fancybox=True, loc='upper left')
ax.annotate("$f_{X|H_0}(x|H_0)$", xy=(-0.6, 0.35), xycoords='data',
xytext=(-90, 20), textcoords='offset points',
size=30, ha='right',
arrowprops=dict(arrowstyle="->", color='black',
connectionstyle="arc3,rad=0.1"))
ax.annotate("$f_{X|H_1}(x|H_1)$", xy=(1.6, 0.35), xycoords='data',
xytext=(100, 20), textcoords='offset points',
size=30, ha='left',
arrowprops=dict(arrowstyle="->", color='black',
connectionstyle="arc3,rad=0.1"))
plt.grid(color='black', linestyle='--', linewidth=1, alpha=0.3);
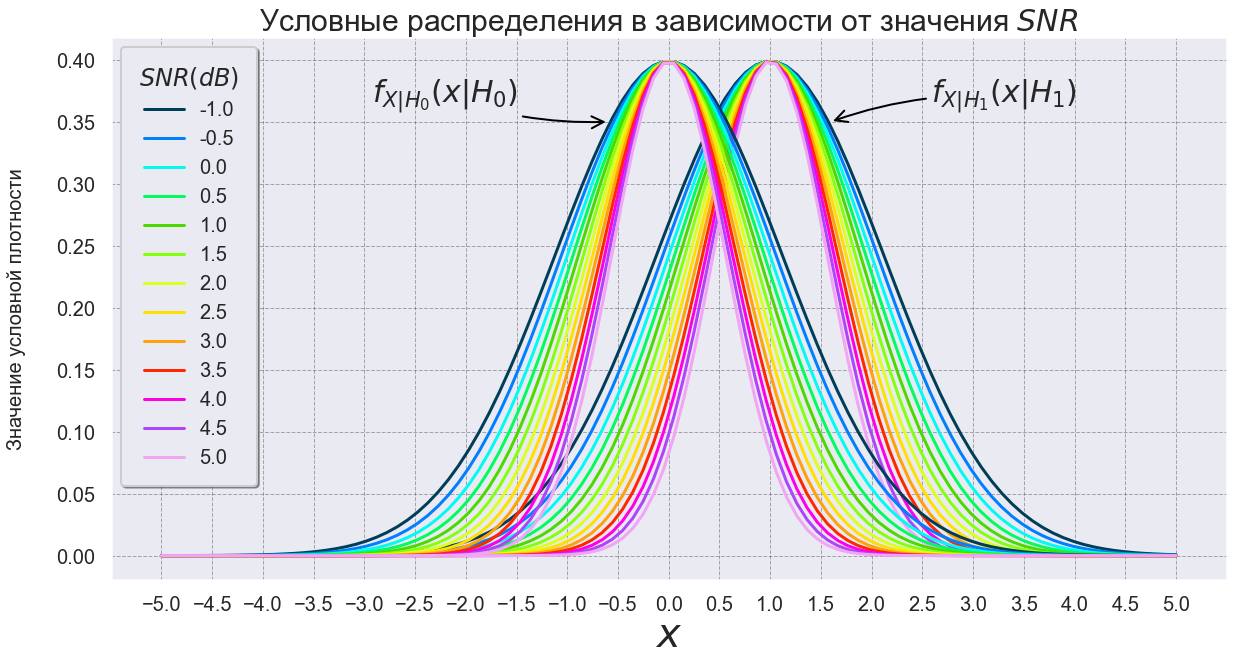
. 7 , , , , , .
:
data4 = []
for SNR in SNR_values:
for lambda_ in lambda_values:
Pfa, Pd = roc_curve(snr_to_sigma(SNR), lambda_)
data4.append([Pfa, Pd, str(SNR), lambda_])
data4 = pd.DataFrame(data4, columns=['Pfa', 'Pd', 'SNR', 'lambda'])
fig, ax = plt.subplots(figsize=(16, 12))
sns.set_context('poster')
plt.title(' $P_d$ $\lambda$ $SNR$', fontsize=40)
plt.xlabel('$\lambda$', fontsize=40)
plt.xticks(np.arange(0, 1.05, 0.1), fontsize=20)
plt.yticks(np.arange(0.5, 1.05, 0.1), fontsize=20)
plt.ylabel('$P_d$', fontsize=40, rotation=0, labelpad=40)
sns.lineplot(x='lambda', y='Pd', hue='SNR',
data=data4, palette='gist_ncar', ax=ax)
ax.annotate(" $\lambda$", xy=(0.5, 0.85), xycoords='data',
xytext=(-10, 50), textcoords='offset points',
size=20, ha='right',
arrowprops=dict(arrowstyle="->", color='black',
connectionstyle="arc3,rad=-0.2"))
plt.grid(color='black', linestyle='--', linewidth=1, alpha=0.3)
plt.legend(fontsize='small', shadow=True, title='$SNR(dB)$',
borderpad=0.9, fancybox=True);
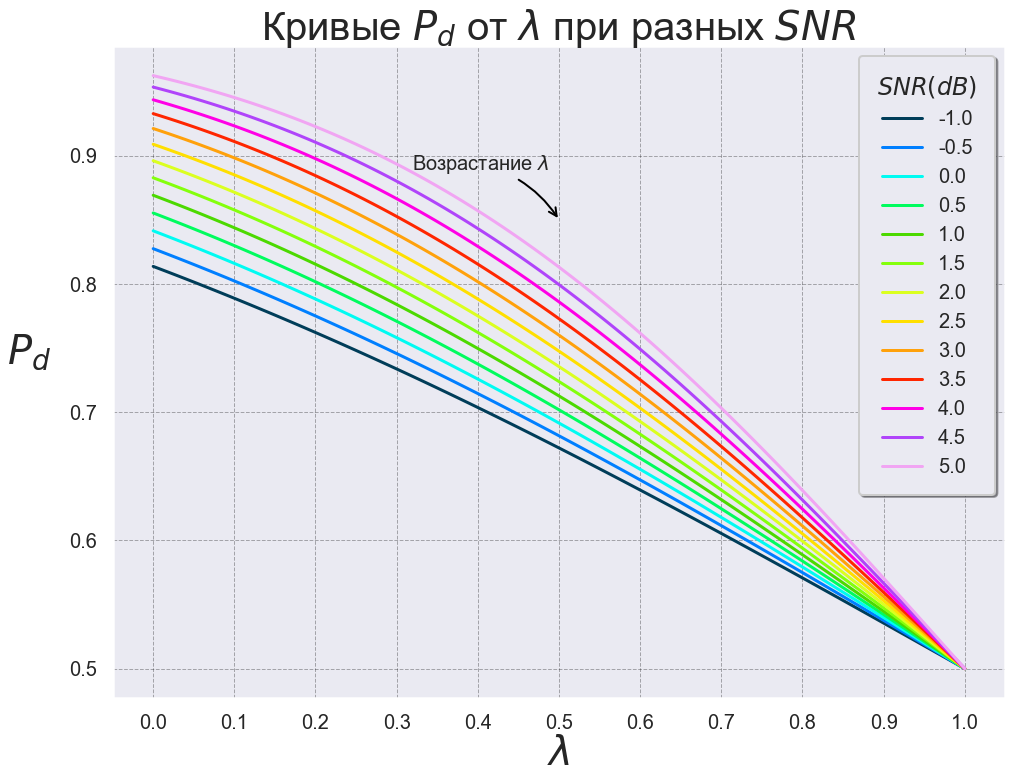
. :
fig, ax = plt.subplots(figsize=(16, 12))
sns.set_context('poster')
plt.title(' $P_{fa}$ $\lambda$ $SNR$', fontsize=40)
plt.xlabel('$\lambda$', fontsize=40)
plt.ylabel('$P_{fa}$', fontsize=40, rotation=0, labelpad=40)
sns.lineplot(x='lambda', y='Pfa', hue='SNR',
data=data4, palette='gist_ncar', ax=ax)
ax.annotate(" $\lambda$", xy=(0.5, 0.35), xycoords='data',
xytext=(-10, 90), textcoords='offset points',
size=30, ha='right',
arrowprops=dict(arrowstyle="->", color='black',
connectionstyle="arc3,rad=0.2"))
plt.grid(color='black', linestyle='--', linewidth=1, alpha=0.3)
plt.legend(fontsize='small', shadow=True, title='$SNR(dB)$',
borderpad=0.9, fancybox=True);
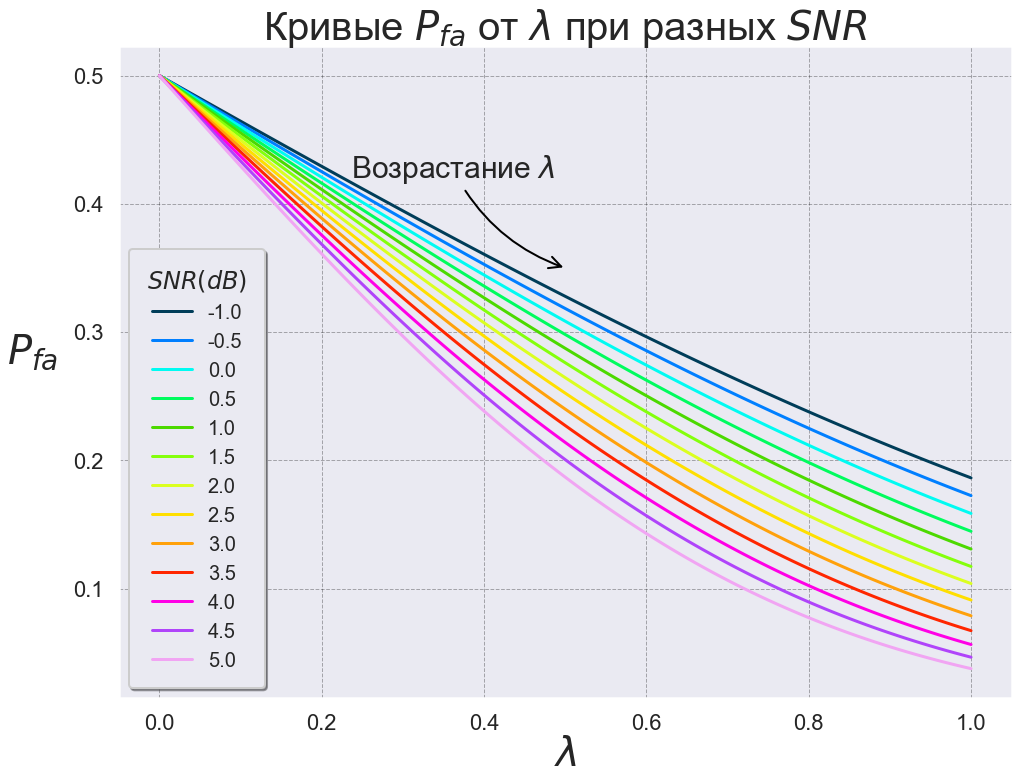
,
,
,
, .
, ROC-
,
.
:
:
, ROC-
. ,
, ,
.
,
, ..
( ).
# , Pfa Pd sigma lambda
def dif_roc_curve(sigma, lambda_):
return (derivative(lambda x: 1 - norm.cdf(x/sigma), lambda_, dx=1e-10),
derivative(lambda x: 1 - norm.cdf((x - 1)/sigma), lambda_, dx=1e-10))
data5 = []
for SNR in SNR_values:
for lambda_ in [0, 0.5, 1]:
dPfa, dPd = dif_roc_curve(snr_to_sigma(SNR), lambda_)
Pfa, Pd = roc_curve(snr_to_sigma(SNR), lambda_)
tan = dPd/dPfa
for i in np.arange(0.01/tan, 0.2/tan, 0.01/tan):
data5.append([tan*(i - Pfa) + Pd, i, str(SNR), lambda_])
data5 = pd.DataFrame(data5, columns=['y', 'x', 'SNR', 'lambda'])
fig, ax = plt.subplots(figsize=(18, 14))
sns.set_context('poster')
plt.title('$ROC$- $3^{}$ ', fontsize=40)
plt.xlabel('$P_{fa}$', fontsize=40)
plt.xticks(np.arange(0, 1.05, 0.1), fontsize=20)
plt.yticks(np.arange(0, 1.05, 0.1), fontsize=20)
plt.ylabel('$P_d$', fontsize=40, rotation=0, labelpad=40)
sns.lineplot(x='Pfa', y='Pd', hue='SNR', legend=False,
data=data[data['SNR'] == '5.0'], palette='gist_ncar', ax=ax)
sns.lineplot(x='x', y='y', hue='lambda', linestyle='--',
data=data5[data5['SNR'] == '5.0'],
palette='dark:b', legend=True, ax=ax)
plt.grid(color='black', linestyle='--', linewidth=1, alpha=0.3)
plt.legend(fontsize='small', shadow=True, title=' $\lambda=$',
borderpad=0.9, fancybox=True, loc=4);
/
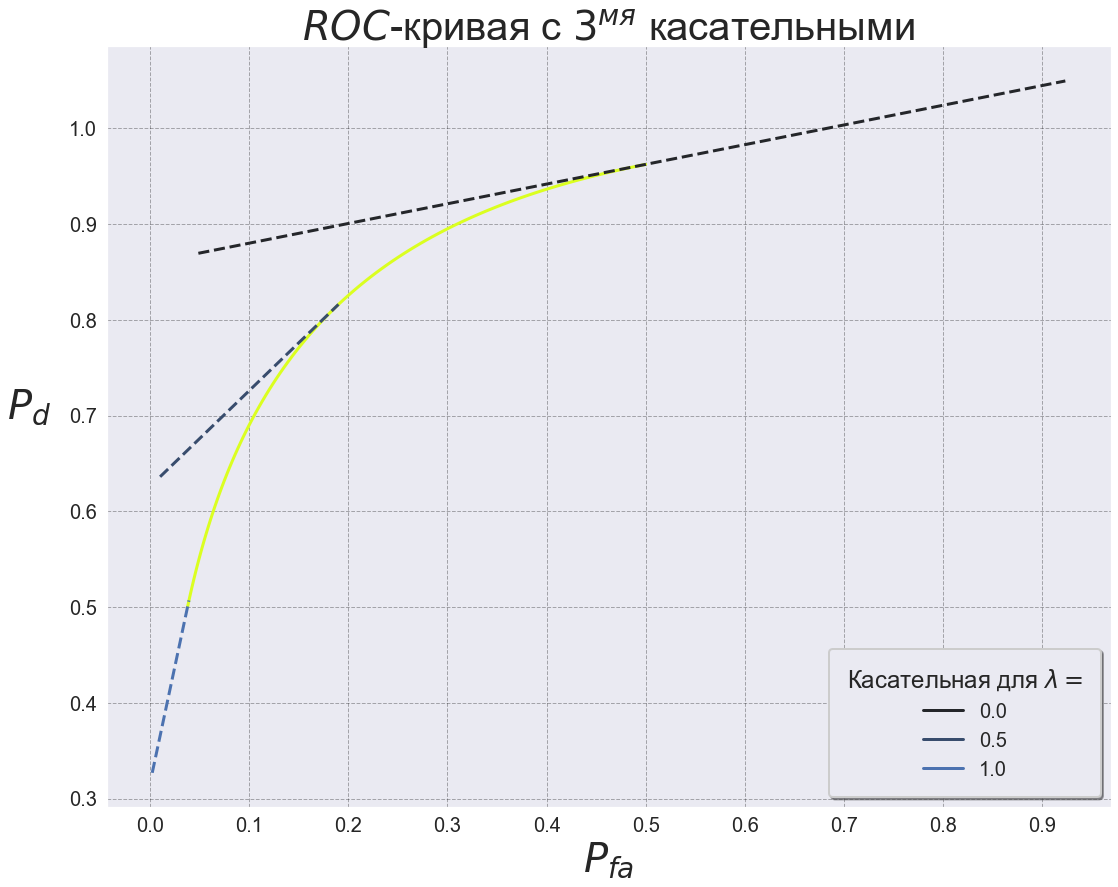
. 10 .
ROC- . ROC- . , ,
,
. , ROC-,
.
- . , . 1. , --, 1968, , . , . . . . . ., « », 1972, 744 .
Tyapkin V.N. Fundamentos de la construcción de estaciones de radar de tropas radio-técnicas: libro de texto / V.N. Tyapkin, A.N. Fomin, E.N. Garin [et al.]; debajo del total. ed. V.N. Tyapkin. - Krasnoyarsk: Sib. Feder. un-t. - 2011 .-- 536 p.
Adicionalmente
Enlace a github con código fuente.