En un trabajo reciente, se estableció un nuevo récord de velocidad para multiplicar dos matrices . También marca el final de una era para el método que los científicos han utilizado para la investigación durante décadas.
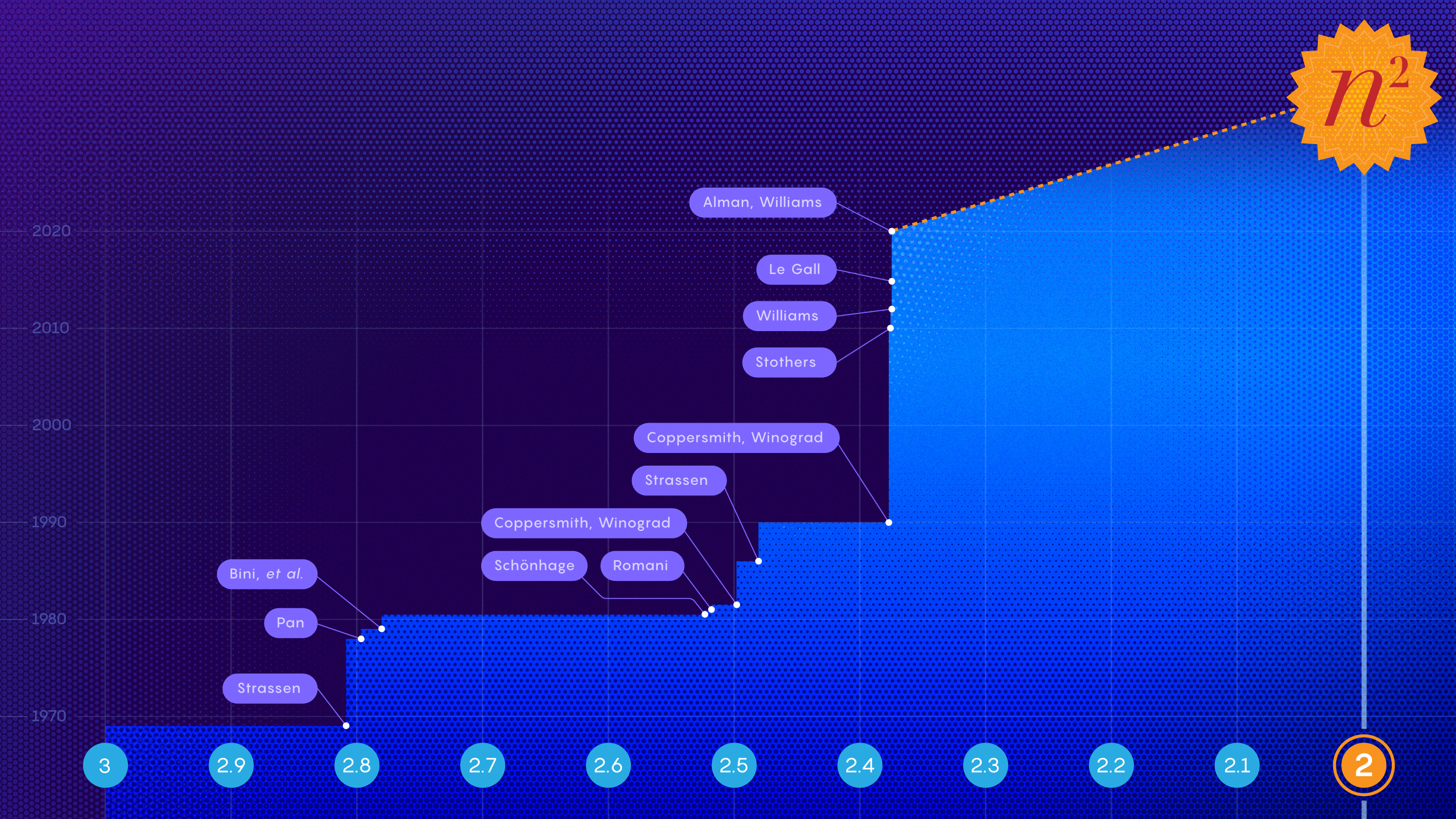
Los matemáticos se esfuerzan por lograr un objetivo mítico: el segundo grado (exponente dos), es decir, multiplicar un par de n x n matrices en solo n 2 pasos. Los investigadores se están acercando a su objetivo, pero ¿podrán lograrlo alguna vez?
Para los informáticos y matemáticos, la idea misma del "segundo grado" está asociada con la idea de un mundo perfecto.
“Es difícil distinguir entre el pensamiento científico y la ensoñación infundada”, admite Chris Umans del Instituto de Tecnología de California. "Quiero que el título sea dos porque es hermoso".
Desde el punto de vista del número requerido de pasos, "segundo grado" es la velocidad de ejecución ideal.una de las operaciones matemáticas más fundamentales es la multiplicación de matrices. Si se puede alcanzar el segundo grado, entonces la multiplicación de matrices se puede realizar lo más rápidamente posible físicamente. Si este no es el caso, entonces estamos atrapados en un mundo que no está a la altura de nuestros sueños.
Las matrices son arreglos de números. Cuando las dos matrices concuerdan (el número de columnas en el primer factor es igual al número de filas en el segundo), se pueden multiplicar para obtener el tercero. Por ejemplo, si comienza con un par de matrices de 2 x 2, su producto también será una matriz de 2 x 2 que contiene cuatro elementos. De manera más general, el producto de un par de n x n matrices es otra n x n matriz con n 2 elementos.
Por lo tanto, el menor número posible de pasos para multiplicar pares de matrices es n 2 , es decir, el número de pasos necesarios solo para escribir la respuesta. De ahí el nombre de "segundo grado".
Y aunque nadie sabe con certeza si esto se puede lograr, los investigadores continúan avanzando en esta dirección.
El artículo, publicado en octubre, se acerca aún más a la meta y describe el método más rápido de multiplicar dos matrices hasta ahora. El resultado recibido por Josh Alman , estudiante de doctorado en la Universidad de Harvard, y Virginia Wasilewska Williamsdel Instituto de Tecnología de Massachusetts, reduce el grado del mejor anterior en aproximadamente una cien milésima. Este es realmente un gran logro en esta área, logrado a través de un trabajo minucioso.
Para comprender mejor este proceso y cómo se puede mejorar, comencemos con un par de matrices 2 x 2, A y B. Al calcular cada elemento de su producto, use la fila correspondiente de A y la columna correspondiente de B. Para obtener el elemento superior derecho, multiplique el primer número en la primera fila A por el primer número en la segunda columna B, luego multiplique el segundo número en la primera fila A por el segundo número en la segunda columna B y sume los dos productos.

Samuel Velasco / Quanta Magazine
Esta operación se conoce como obtener un "producto escalar" de una fila con una columna (a veces llamado "producto interno"). Para calcular otros elementos en el producto de la matriz, repita el procedimiento con las filas y columnas correspondientes.
En general, el método clásico de multiplicación de matrices 2 x 2 consta de ocho multiplicaciones y varias sumas. Normalmente, este método de multiplicar dos n x n matrices requiere n 3 multiplicaciones.
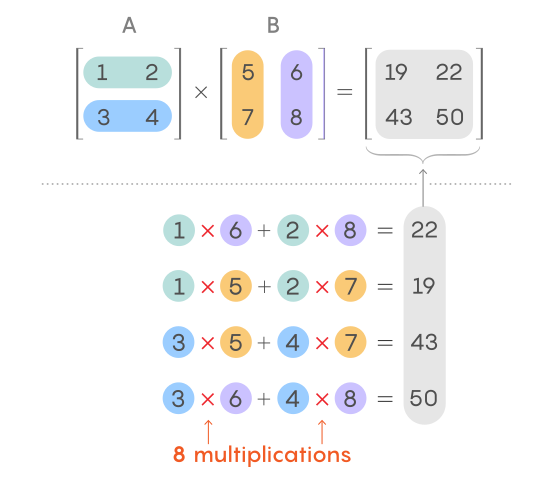
A medida que aumenta el tamaño de las matrices, el número de multiplicaciones necesarias para encontrar su producto crece mucho más rápido que el número de adiciones. Para encontrar el producto de matrices 2 x 2, solo se requieren ocho multiplicaciones intermedias, y para encontrar el producto de matrices 4 x 4, ya hay 64. Sin embargo, el número de adiciones requeridas para obtener la suma de estas matrices es no muy diferente. Por lo general, el número de adiciones es igual al número de elementos en la matriz, es decir, cuatro para matrices de 2 x 2 y 16 para matrices de 4 x 4. Esta diferencia entre la suma y la multiplicación deja en claro por qué los investigadores miden la velocidad de la multiplicación de matrices. únicamente en términos del número de multiplicaciones necesarias.
“Las multiplicaciones lo son todo”, dice Uman. “El exponente al final depende completamente del número de multiplicaciones. Las adiciones desaparecen en cierto sentido ".
Durante siglos, la gente creyó que n 3 era la forma más rápida de multiplicar matrices . En 1969, Volker Strassen, según se informa, se propuso demostrar que es imposible multiplicar matrices 2 x 2 utilizando menos de ocho multiplicaciones. Aparentemente, todavía no podía encontrar pruebas, y después de un tiempo entendió por qué: de hecho, ¡hay una manera de hacer esto usando siete multiplicaciones!
A Strassen se le ocurrió un conjunto complejo de relaciones que le permitieron reemplazar una de estas ocho multiplicaciones con 14 adiciones adicionales. La diferencia puede parecer una diferencia sutil, pero vale la pena porque la multiplicación contribuye más que la suma. Al encontrar una manera de deshacerse de una multiplicación para matrices pequeñas de 2 x 2, Strassen descubrió una posibilidad que podía usar al multiplicar matrices más grandes.
“Este pequeño cambio se traduce en enormes mejoras en el manejo de matrices grandes”, dice Williams.


Virginia Wasilewska Williams del Instituto de Tecnología de Massachusetts y Josh Alman de la Universidad de Harvard descubrieron la forma más rápida de multiplicar dos matrices en n 2,3728596 pasos. Jared Charney; Richard T.K. Halcón
Suponga que desea multiplicar un par de matrices de 8 x 8. Una forma de hacerlo es dividir cada matriz grande en cuatro matrices de 4 x 4 de modo que cada una tenga cuatro elementos. Dado que los elementos de una matriz también pueden ser matrices, puede pensar en las matrices originales como un par de matrices de 2 x 2, cada uno de los cuatro elementos de los cuales es en sí mismo una matriz de 4 x 4. Con alguna manipulación, cada uno de estos 4 x 4 matrices se pueden dividir en cuatro matrices de tamaño 2 x 2.
La idea detrás de esta división múltiple de matrices grandes en matrices más pequeñas es que puede aplicar el algoritmo de Strassen a matrices más pequeñas una y otra vez y usar su método para reducir el número de pasos. en cada paso. En general, el algoritmo de Strassen aumentó la velocidad de la multiplicación de matrices con n 3 an 2,81 pasos multiplicativos.
El siguiente paso importante en el desarrollo de la idea tuvo lugar a fines de la década de 1970, cuando apareció un enfoque fundamentalmente nuevo para resolver este problema. Implica traducir la multiplicación de matrices en otro problema de álgebra lineal computacional utilizando objetos llamados tensores. Los tensores utilizados en este problema son matrices tridimensionales de números formadas por muchas partes diferentes, cada una de las cuales parece un pequeño problema de multiplicación de matrices.
La multiplicación de matrices y este problema de tensor son, en cierto sentido, equivalentes entre sí, pero los investigadores ya tenían procedimientos más rápidos para resolver este último. Así, se enfrentaron a la tarea de determinar el "tipo de cambio" entre ellos: ¿Qué tamaño de matrices se pueden multiplicar con los mismos costos computacionales que se requieren para resolver el problema del tensor?
“Este es un concepto muy común en la informática teórica: transformar tareas y establecer analogías entre ellas para mostrar que son igualmente simples o complejas”, dijo Alman.
En 1981, Arnold Schönhage utilizó este enfoque para demostrar que la multiplicación de matrices se puede realizar en n 2.522 pasos. Strassen más tarde llamó a este enfoque el "método láser" .
Durante las últimas décadas, todas las mejoras en la multiplicación de matrices provienen de mejoras en el método láser a medida que los investigadores han encontrado formas más eficientes de transformar el problema. En su nueva demostración, Alman y Williams desdibujan la distinción entre los dos problemas y muestran que es posible reducir el número de multiplicaciones. “En general, Josh y Virginia encontraron una manera de aplicar la computación en máquina dentro del método láser y obtuvieron los mejores resultados hasta la fecha”, dijo Henry Cohn.de Microsoft Research.
En su artículo, el límite teórico de la velocidad de multiplicación de matrices se mejora hasta n 2,3728596 .
También gracias a esta investigación, Williams puede recuperar la corona en el campo de la multiplicación de matrices, que recibió legítimamente en 2012 (n 2.372873 ), y luego perdió en 2014 ante François Le Gall (n 2.3728639 ).
Pero, a pesar de todas estas carreras y victorias, queda claro que en el caso de este enfoque, opera la ley de rendimientos decrecientes o rendimientos decrecientes. Lo más probable es que la mejora de Alman y Williams agotara casi por completo las posibilidades del método láser, pero no permitió alcanzar el objetivo teórico final.
"Es poco probable que pueda acercarse al segundo grado utilizando esta familia de métodos", dijo Umans.
Esto requerirá el descubrimiento de nuevos métodos y una fuerte creencia de que es posible.
Williams recuerda una de sus conversaciones con Strassen sobre esto: “Le pregunté si pensaba que era posible obtener el segundo grado para la multiplicación de matrices, y me respondió:“ ¡No, no, no, nunca! ”.