
Recientemente hice un proyecto en el que la variable de destino era de varias clases, por lo que estaba buscando formas adecuadas de codificar características categóricas. Encontré muchos artículos que enumeran los beneficios de codificar a través de la variable de destino sobre otros métodos, y cómo realizar esta tarea en dos líneas de código utilizando la biblioteca category_encoders . Sin embargo, para mi sorpresa, descubrí que ningún artículo demostraba este método para una variable objetivo multiclase. Revisé la documentación de category_encoders y me di cuenta de que la biblioteca solo funciona para variables binarias o reales, miré el trabajo original de Daniele Micci-Barreca, que introdujo la codificación del objetivo medio y tampoco encontró nada sensato.
En este artículo, daré una descripción general del documento que describe la codificación de destino y mostraré con un ejemplo cómo funciona la codificación de destino para problemas binarios.
Teoría
Entonces: si se le pregunta "0/1", "clic en / sin clic" o "gato / perro", entonces su problema de clasificación es binario; si desea responder "rojo, verde o azul, pero tal vez amarillo" o "sedán versus hatchback y todo versus SUV", entonces el problema está en varias clases.
Esto es lo que tiene que decir el artículo de objetivos categóricos que mencioné anteriormente:
El resultado de cualquier observación se puede mostrar mediante una estimación de la probabilidad de la variable objetivo.
, , .
.
, .
. 0, 1. P (Y = 1 | X = Xi), ..:

n(Y) - 1 ,
n(i) - i- ,
n(iY) - 1 i- .
, 1 i- , - 1 . λ - , 0 1, n(i), .
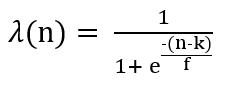
TargetEncoder category_encoders, k - min_sample_leaf, f - .
, , , . , , , (. . Y). .
. . , . , , , . .
, .
.
, 1, «»?
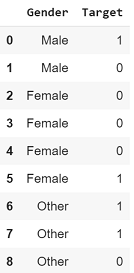
: 1/2 = 0,5.
, , Target 1, «»?
: 1/4 = 0,25.
?
, «Female» 0,25, . , 4/9 = 0,4.
, «» , , .
min_sample_leaf, k = 1 , f = 1,
«Male», n = 2;
λ(‘Male’)=1/(1+exp(-(2–1)/1))=0.73 # Weight Factor for 'Male'
Target Statistic=(Weight Factor * Probability of 1 for Males)
+ ((1-Weight Factor) * Probability of 1 Overall)S(‘Male’)= (0.73 * 0.5) + ((1–0.73) * 0.4) = 0.485
, «Female» , n = 4;
λ(‘Female’)=1/(1+exp(-(4–1)/1))=0.95 #Weight Factor for 'Female'
Target Statistic=(Weight Factor * Probability of 1 for Females)
+ ((1-Weight Factor) * Probability of 1 Overall)S(‘Female’)= (0.95 * 0.25) + ((1–0.95) * 0.4) = 0.259
, , λ , . 4 «Female», 2 «Male». 0,95 0,73.
, «Male» 0,485 , «Female» 0,259. «».
! !
?
, , category_encoders:
!pip install category_encoders
import category_encoders as ce
x=['Male','Male','Female','Female','Female','Female','Other','Other','Other']
y=[1,0,0,0,0,1,1,1,0]
print(ce.TargetEncoder().fit_transform(x,y))
TargetEncoder category_encoders. , . , .
, .
!