Hola a todos. Continuamos con esta serie de artículos sobre lo que la ciencia de datos puede proporcionar para predecir COVID-19. El primer artículo está aquí . Hoy hablaremos sobre la segunda clase de modelos para predecir la dinámica de propagación de COVID-19. Se basan en supuestos sobre un aumento de la incidencia y describen la situación a medio y largo plazo. Estamos hablando con Nikolay Kobalo, ingeniero de datos senior de CFT.
Recordemos las condiciones que tenemos:
Dadas: Colosales capacidades de ciencia de datos, tres talentosos especialistas.
Buscar: formas de predecir la propagación de COVID-19 con una semana de anticipación.
Pasemos a la segunda solución.
- Kolya, hola. Díganos qué modelo utilizó para resolver este problema.
- Cogí uno de los modelos que, en mi opinión, mejor se adapta a la ocasión. El modelo se presenta en forma de ecuación diferencial y consta de cuatro funciones:
1. El número de personas susceptibles de contraer esta infección;
2. El número de portadores, es decir, personas que ya se han infectado, pero que aún no lo saben;
3. El número de personas enfermas que infectan a otros;
4. El número de recuperados.
Como puede ver, este modelo no tiene en cuenta la mortalidad por covid. Puedes ver los detalles del modelo en mi github: https://github.com/rerf2010rerf/COVID-19-forecast/blob/master/public.ipynb
El modelo se llama SEIR y pertenece a una familia de modelos compartimentados que describen la propagación de una epidemia. Los modelos de esta familia permiten describir diferentes tipos de infecciones. Por ejemplo, aquellos para los que se desarrolla inmunidad (o, por el contrario, no se desarrolla). O los que tienen (o no tienen) período de incubación. En el caso del COVID-19, utilicé un modelo con un período de incubación y la inmunidad que se producía en personas que habían estado enfermas.
Todos los modelos polígamos son sistemas de ecuaciones diferenciales de primer orden. Para SEIR se ven así:

Aquí:
S (t) - (Susceptible) - el número de personas susceptibles a la infección.
E (t) - (Expuesto) - el número de portadores, es decir personas infectadas en las que la enfermedad aún no se ha manifestado debido al período de incubación.
Yo (t) - (Infeccioso) - infectado.
R (t) - (Recuperado) - recuperado.
N = S + E + I + R - tamaño de la población. Permanece constante, es decir se supone que nadie muere a causa de la enfermedad.
μ es la tasa de mortalidad natural.
α es el recíproco del período de incubación de la enfermedad.
γ es el recíproco del tiempo medio de recuperación.
β es el coeficiente de intensidad de los contactos que conducen a la infección.
El ciclo de vida de un individuo en el modelo SEIR se ve así:

Una persona sana, pero aún no enferma (Susceptible) puede infectarse a partir de una persona infectada (Infecciosa). La probabilidad de que una persona sana se infecte se describe mediante el parámetro β.
Una persona infectada entra en un estado de portador de la infección (expuesto). Los portadores son personas en las que la enfermedad aún no se ha manifestado, es decir, tienen un período de incubación. Los transportistas no pueden infectar a nadie. La transición de las personas susceptibles a la enfermedad al estado de portadores se describe mediante las dos primeras ecuaciones del modelo (utilizando el término β (I / N)).
Después de 1 / α días (período de incubación) después de la infección, el portador entra en estado infectado (infeccioso).
Después de 1 / γ días (tiempo de recuperación), la persona infectada entra en el estado Recuperado. La persona recuperada desarrolla inmunidad y ya no puede contraer esta infección.
El modelo también prevé la mortalidad natural de la población en la población. La mortalidad en el modelo SEIR se equilibra con la fecundidad, por lo que la población total no cambia. Al mismo tiempo, disminuirá el número de personas recuperadas en la población, ya que los recién nacidos no tendrán inmunidad. En consecuencia, el número de personas que se han recuperado en la población disminuye con el tiempo. La tasa de mortalidad se describe mediante el parámetro μ.
- Tienes coeficientes en el modelo. Entonces, ¿hiciste alguna suposición?
- Una de mis suposiciones fue que la mortalidad natural en la población se puede descuidar, es decir, μ = 0. Esta suposición parece válida, ya que queremos predecir la propagación de la infección en un período corto de tiempo, solo unos pocos meses.
Además, el modelo elegido asume que quienes se han recuperado se vuelven inmunes a la infección, es decir, no pueden volver a infectarse.
- ¿Y esto es así, por cierto?
- Parece que sí. Ya se han registrado varias reinfecciones, pero la mayoría de las veces esto no sucede. Por tanto, podemos decir que es así.
- ¿Y cuál es su “factor de intensidad de contacto”?
“Aquí me refiero a la intensidad con la que las personas entran en contacto entre sí y se infectan. En términos generales, esta es la probabilidad de que cuando dos personas se encuentran, donde una está infectada y la otra no, la segunda finalmente se enferme.
- ¿Cuanto es eso? ¿Cerca de uno?
- No, seleccioné este parámetro de acuerdo con los datos. Depende del nivel de autoaislamiento. Por ejemplo, si una gran parte de la población no entra en contacto con otras personas, entonces el coeficiente se reduce, y si la población se comunica activamente entre sí, aumenta.
- Okey. ¿También tienes un tiempo de recuperación? ¿Ambos alfa y gamma?
- Tomé el alfa igual a 1 / 5.1, este era un parámetro conocido para COVID-19 (el parámetro inverso al período de incubación en días). Y seleccioné la gama de acuerdo con los datos. Este es el "tiempo de convalecencia". Por cierto, la "intensidad de los contactos" también se basa en los datos.
- Oh bien. Por otra parte, ¿puede decirnos qué suposiciones hacen los modelos? ¿Qué significa cada ecuación?
- La primera ecuación describe el cambio en el número de susceptibles a la infección. En particular, el tercer término dice que cuanto más intensos son los contactos entre los infectados y los susceptibles, más rápido disminuye el número de susceptibles. Además, si alguien se infectó y luego se infectó, ya no está incluido en este número. Al comienzo de la epidemia, es igual al número de personas de la población.
Luego, se toma el número de portadores de aquellos susceptibles a la infección, es decir, una persona se comunica con una persona infectada, se infecta y se convierte en portadora de la infección. Esto se describe en la segunda ecuación. Dice que la tasa de crecimiento de los portadores es mayor cuanto más intensos son los contactos entre susceptibles e infectados y, por el contrario, menos, menos portadores quedan en este momento.
La tercera ecuación dice que la tasa de crecimiento de los infectados es mayor, más portadores hay ahora (que se vuelven infectados), y cuanto menos, más infectados ya hay.
La cuarta ecuación describe la tasa de crecimiento de quienes se han recuperado, que es cuanto mayor, más infectados (que se pueden recuperar), y cuanto menos, más recuperados ya hay.
- Suena como una descripción del desarrollo de la situación.
- De hecho, existen diferentes modelos. Este es el modelo SEIR, y hay SIR, en el que no hay susceptibles a la infección. Hay modelos con más parámetros. Hay un modelo que prevé la mortalidad por infección, pero yo no lo usé.
- ¿Dónde encontraste este modelo?
- Buscado en Google. Hay un artículo en Wikipedia. Artículos adicionales encontrados.
- También presentó los gráficos.
- Este gráfico es un ejemplo. No se basa en datos reales. Simplemente muestra cómo se comporta el modelo. Ella predice que todos eventualmente se enfermarán y mejorarán.

- Está bien, te lo llevaste todo, ¿y luego qué?
- Tomé los datos que están disponibles por país. Supuso que la tasa de mortalidad es cero. Reescriba los difours en forma de diferencias finitas:

como operador de diferencias finitas en esta solución, se usa una diferencia de dos lados.
El número de personas recuperadas R por día está en los datos iniciales y el número de infectados I es igual al número de casos confirmados menos el número de recuperados. Entonces, a partir de la última ecuación, podemos encontrar γ optimizando la función objetivo MACHO (ΔR-γI).
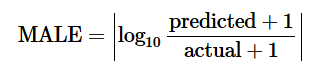
Para rastrear cómo las medidas de cuarentena afectan el desarrollo de la epidemia, compliqué un poco mi tarea y reemplacé el coeficiente β con la función β (t); después de todo, a medida que se introduce la cuarentena en el país, la tasa de infección debería disminuir, lo que significa que en nuestro caso β no será constante. Como ya tenemos todas las condiciones iniciales para resolver el difur, podemos usar la optimización para encontrar la función β (t).
- ¿Este es un día de diferencia?
- Día menos el día anterior. Introduje los datos y calculé los coeficientes desconocidos.
- ¿Beta y gamma?
- Tomé Alpha 5.1 días. En consecuencia, fue necesario encontrar beta y gamma: la intensidad de los contactos y el tiempo de recuperación.
- ¿Y que te paso?
- Hay gráficos. Cada región y cada país resultó ser diferente. Decidí para cada país por separado. A la izquierda hay un gráfico de datos (negro - era real, rojo - infectado y recuperado, predicho por el modelo). Infectado + recuperado - resulta que E + R. A la derecha está el gráfico del coeficiente beta. Beta, por cierto, se supone que depende del tiempo. Aquí, el mayor salto en β coincide con el momento de la cuarentena el 30 de marzo.
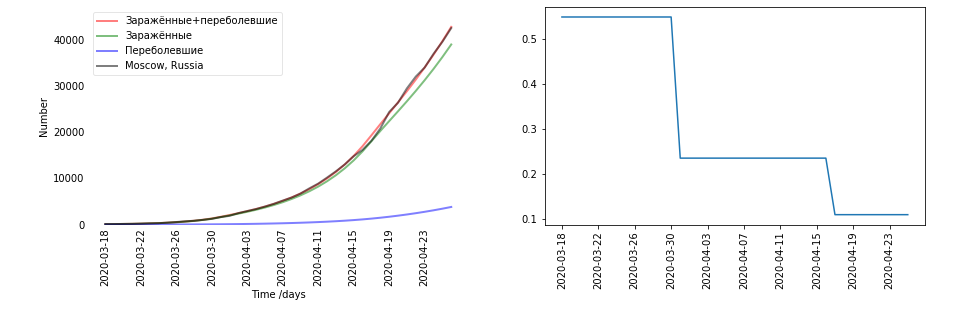
- ¿Y lo contó de acuerdo con los datos o lo asumió?
- Esto ya está calculado según los datos. Este es exactamente el resultado del entrenamiento en Moscú.
- ¿Estableció usted mismo los umbrales de tiempo?
- Pensé que la función tiene una forma de dos etapas. Y optimizado. Simplemente ajusto los datos y encuentro las funciones óptimas que mejor encajan. También intenté usar funciones con un número diferente de peldaños, pero las de dos etapas mostraron mejores resultados.
- Echemos un vistazo a los países, por ejemplo, Italia. Bueno, aquí tienes una imagen diferente ...

- En Italia, la cuarentena, aparentemente, funcionó mejor. Y hay más personas que han estado enfermas. El modelo confirmó que la cuarentena se introdujo el 9 de marzo.
- ¿Qué eligió para el pronóstico final?
- Para el pronóstico final, elegí una intensidad constante de contactos y construí un modelo usando los dos últimos puntos. Es decir, conocemos toda la historia anterior, pero tomamos solo los últimos puntos.
- ¿Esto es para la predicción de la semana?
- Sí. Y lo que pasó antes fue ver cómo se comporta el modelo. Y luego ya miré qué función es mejor tomar y cuántos puntos estudiar.
- Probablemente, si quisiera pronosticar hasta ahora, habría recibido una decisión diferente. ¿Tiene algo que muestre cómo la situación puede desarrollarse más?
- Sí. Pero no es muy interesante ahí. Ella predijo que todos en Moscú estarían enfermos en septiembre.
- En una de las reuniones dijiste que, según tu pronóstico, el pico debería haber sido en julio. De hecho, todo sucedió un poco antes. ¿Qué crees que no tuvo en cuenta el modelo?
- Probablemente beta. Quizás la cuarentena se ha intensificado. Es posible que la intensidad de los contactos haya disminuido debido al hecho de que las personas han estado enfermas, no infectan y no se infectan. Beta debería de alguna manera depender de ello. Y aquí no se tiene en cuenta.
- Bueno, es decir, ¿dices que podemos regular todo con una beta?
- Según los datos conocidos, sí, podemos, con los ajustes beta y gamma.
- ¿Tu modelo predice la próxima ola?
- No, todo es estable: crece, crece, crece y todos se enfermarán. Aunque también existe un factor de estacionalidad. Períodos de otoño, por ejemplo (cuando la gripe, etc., el sistema inmunológico se debilita). Pero el modelo no tiene todo esto en cuenta.
- ¿Cuáles son los pros y los contras de su modelo?
- En el momento de la compilación del modelo, se conocían pocos datos. Ahora ya se conocen tanto el período de recuperación como el período de incubación (entonces era 5.1, ahora se mide con mayor precisión). De los profesionales: muestra el proceso en sí, cómo va. Y si investigamos más profundamente en el ejemplo de otros países, por ejemplo, Italia, Alemania, cómo estos beta influyeron, entonces sería posible refinar este modelo y construir un pronóstico a largo plazo más preciso.
, data science – .
, , . - – , , , , .
, , . .Hizo el modelo más genial;)