La pregunta de David Hilbert sobre los polinomios de séptimo grado, que durante mucho tiempo se consideró resuelta, abrió una nueva red de conexiones matemáticas para los investigadores.
El éxito en matemáticas es raro. Pregúntale a Benson Farb .
"El problema con las matemáticas es que el 90 por ciento de las veces fracasas y tienes que ser la persona que pueda aceptarlo", dijo Farb una vez durante una cena con amigos. Cuando uno de los invitados, también matemático, se sorprendió de que Farb tuviera éxito hasta el 10% de las veces, Farb admitió: "No, no, exageré mucho mi tasa de éxito".
Farb, topólogo de la Universidad de Chicago, se enfrentó felizmente a su último revés, aunque, para ser justos, no fue del todo su mérito. La pregunta está relacionada con un problema, paradójicamente resuelto y no resuelto, abierto y cerrado.
El problema es el 13 de 23 problemas matemáticos que no se resolvieron a principios del siglo XX. Luego, el matemático alemán David Hilbert hizo esta lista , que, en su opinión, determinó el futuro de las matemáticas. El problema está relacionado con la resolución de ecuaciones polinómicas de séptimo grado. Un polinomio es una secuencia de términos de una ecuación, cada uno de los cuales consta de un coeficiente numérico y variables elevadas a una potencia; los términos están conectados entre sí por suma y resta. El séptimo grado significa el mayor exponente de todas las variables.
Los matemáticos ya han aprendido a resolver con destreza y rapidez ecuaciones de segundo, tercer y, en algunos casos, cuarto orden. Estas fórmulas, incluida la conocida fórmula cuadrática para el segundo grado, incluyen operaciones algebraicas, es decir, aritmética y extracción de raíces. Pero cuanto mayor es el exponente, más confusa es la ecuación y se vuelve cada vez más difícil de resolver. El decimotercer problema de Hilbert es la cuestión de si la solución de una ecuación de séptimo orden se puede expresar en términos de un conjunto de sumas, restas, multiplicaciones, divisiones y funciones algebraicas en como máximo dos variables.

En 1900, David Gilbert compiló una lista de 23 problemas críticos abiertos.
Respuesta: probablemente no. Para Farb, sin embargo, esto no es solo una cuestión de resolver una ecuación algebraica compleja. Dijo que el problema 13 es uno de los problemas más fundamentales de las matemáticas, ya que plantea preguntas profundas: ¿qué tan complejos son los polinomios y cómo se pueden medir? "Se ha inventado toda una capa de matemáticas modernas para comprender mejor las raíces de los polinomios", dijo Farb.
Este problema lo llevó a él y al matemático Jesse Wolfson de la Universidad de California en Irvine por el agujero del conejo matemático, cuyos movimientos todavía estudian. También trajo a Mark Kissin , un teórico de números de Harvard y un viejo amigo de Farb , a su excavación .
Farb reconoció que aún no han resuelto el decimotercer problema de Hilbert, ni siquiera se han acercado a resolverlo. Sin embargo, desenterraron estrategias matemáticas casi extintas y exploraron los vínculos del problema con varios campos del conocimiento, incluido el análisis complejo, la topología, la teoría de números, la teoría de la representación y la geometría algebraica. Aplicaron sus propios enfoques, en particular, combinando polinomios con geometría y reduciendo el rango de posibles respuestas a la pregunta de Hilbert. Además, su trabajo propone una forma de clasificar polinomios por métricas de complejidad, un análogo de las clases de complejidad relacionadas con el problema no resuelto de la igualdad de las clases P y NP .
"De hecho, fueron capaces de extraer una versión más interesante del interés", en comparación con los estudiados anteriormente, dijo Daniel Litt, matemático de la Universidad de Georgia. "Muestran a la comunidad matemática muchas preguntas naturales e interesantes".
Abierto, cerrado y reabierto
Muchos matemáticos ya pensaban que el problema estaba resuelto. A finales de la década de 1950, el brillante científico soviético Vladimir Igorevich Arnold y su mentor Andrei Nikolaevich Kolmogorov publicaron sus pruebas. Para la mayoría de los matemáticos, el trabajo de Arnold-Kolmogorov cerró esta cuestión. Incluso en Wikipedia - no la verdad última, sino un intermediario bastante razonable en la búsqueda de conocimiento - hasta hace poco el problema estaba marcado como resuelto.

Vladimir Arnold y su mentor Andrei Kolmogorov en la década de 1950 demostraron ser una de las versiones del decimotercer problema de Hilbert, pero, quizás, Hilbert estaba interesado en otra versión del mismo.
Sin embargo, hace cinco años, Farb tropezó con algunas líneas intrigantes en un ensayo de Arnold, donde el famoso matemático reflexiona sobre su trabajo y carrera. Farb se sorprendió al saber que Arnold estaba describiendo el problema 13 como abierto y durante cuarenta años había estado tratando de resolver un problema que parecía haber resuelto.
“Hay trabajos científicos donde simplemente se repite la tesis sobre la solución del problema. Claramente no comprenden el problema en sí ”, dijo Farb. En ese momento, estaba trabajando con Wolfson, entonces un postdoctorado, en un proyecto de topología. Cuando compartió la información que encontró en el trabajo de Arnold, Wolfson se unió al proyecto. En 2017, durante un seminario dedicado al 50 cumpleaños de Farb, Kissin escuchó la charla de Wolsfon y se sorprendió al darse cuenta de que sus ideas sobre polinomios estaban relacionadas con problemas en su trabajo sobre teoría de números. Se unió a su equipo.
La razón de la confusión con este problema pronto quedó clara: Kolmogorov y Arnold resolvieron solo una de sus opciones. Su solución incluía funciones continuas, aquellas que no tienen roturas bruscas o puntos de inflexión. Estas funciones incluyen operaciones familiares como seno, coseno, exponencial y otras más exóticas.
Sin embargo, no todos los investigadores están de acuerdo en que Hilbert estuviera interesado en ellos. "Muchos matemáticos creen que Hilbert se refería a funciones algebraicas, no funciones continuas", dijo Zinovy Reichstein , matemático de la Universidad de Columbia Británica. Farb y Wolfson están trabajando en un problema que creen que Hilbert quería estudiar.
Farb dijo que el problema 13 es un caleidoscopio. “Descubres esto y cuanto más estudias, más direcciones e ideas abre”, dijo. "Abre la puerta a toda una serie de problemas, revela toda la maravillosa red de las matemáticas".
Las raíces del problema
Los matemáticos han estado jugando con polinomios desde la invención de las matemáticas. Las tablillas de piedra de 3.000 años de antigüedad muestran cómo los matemáticos babilónicos utilizaron la fórmula para resolver polinomios de segundo orden. Fue el antecesor cuneiforme de la fórmula cuadrática que se enseña hoy en las lecciones de matemáticas. Fórmula muestra cómo encontrar las raíces de un polinomio, es decir, los valores de x en los que la expresión ax 2 + bx + c, un polinomio de grado dos, se convierte en cero.
Con el tiempo, los matemáticos se interesaron naturalmente en la cuestión de si existen fórmulas tan claras y claras para polinomios de órdenes superiores. "La historia milenaria de este problema es llegar a algo tan poderoso, simple y efectivo", dijo Wolfson.
Cuanto mayor sea el grado del polinomio, más engorrosos se vuelven. En el libro de 1545 Ars Magna [Gran Arte], el erudito italiano Gerolamo Cardano publicó fórmulas para encontrar las raíces de polinomios de tercer y cuarto grado.
Las raíces del polinomio cúbico ax 3 + bx 2 + cx + d = 0 se pueden encontrar usando la siguiente fórmula: La
fórmula para el polinomio de cuarto grado se ve aún peor.
"A medida que crece el grado, también lo hace la complejidad, y la montaña de complejidad se avecina", dijo Kurt McMullen de Harvard. "¿Cómo podemos conquistar esta montaña?"
El matemático italiano Paolo Ruffini en 1799 argumentó que los polinomios de quinto y mayor grado no se pueden resolver mediante operaciones aritméticas y extracción de raíces. En 1824, el matemático noruego Niels Henrik Abel lo demostró. ... En otras palabras, no existe tal fórmula para un polinomio de quinto grado. Afortunadamente, han surgido otras ideas que sugieren formas de estudiar polinomios de grados superiores que se pueden simplificar mediante la sustitución. Por ejemplo, en 1786 el abogado sueco Erland Bring demostró que cualquier ecuación de la forma ax 5 + bx 4 + cx 3 + dx 2 + ex + f = 0 puede reescribirse como px 5 + qx + 1 = 0, donde p y q - números complejos, cuyo valor está determinado por a, b, c, d, e y f. Este hecho abrió nuevos enfoques a las propiedades ocultas de los polinomios.
En el siglo XIX, William Rowan Hamiltoncontinuó el trabajo de Bring y otros. Entre otras cosas, mostró que para encontrar las raíces de un polinomio de sexto grado, solo se necesitan las operaciones aritméticas habituales, raíces cuadradas y cúbicas, y una fórmula algebraica que depende solo de dos variables.
En 1975, el algebrista estadounidense Richard Brower de Harvard introdujo la idea de "grado resolutivo", que describe el número mínimo de términos necesarios para describir un polinomio de algún grado. Menos de un año después, Arnold y el teórico de números japonés Goro Shimura, en otro artículo, introdujeron la misma definición.
En el modelo de Brouwer, el primer intento de sistematizar las reglas para tales sustituciones, el decimotercer problema de Hilbert es si es posible que los polinomios del séptimo grado tengan un grado resolutivo menor que 3. Más tarde, presentó conjeturas similares sobre polinomios de sexto y segundo grado. octavos grados.
Sin embargo, todas estas preguntas se basan en una más general: ¿cuál es el menor número de parámetros necesarios para encontrar las raíces de cualquier polinomio? ¿Cuál es el límite inferior al que puedes llegar?
Pensamiento visual
Un enfoque natural para esta pregunta es imaginar cómo se ven los polinomios. El polinomio se puede escribir como una función, por ejemplo, f (x) = x 2 −3x + 1, - y graficarlo. Luego, la búsqueda de raíces se reduce al hecho de que la función se vuelve igual a cero donde su curva se cruza con el eje x.
Cuanto mayor sea el grado del polinomio, más compleja será su gráfica. Las funciones de tercer orden en tres variables producen superficies lisas pero retorcidas en tres dimensiones. Al saber dónde mirar en estas superficies, los matemáticos pueden aprender mucho sobre la estructura polinomial subyacente.
Como resultado, los intentos de comprender los polinomios involucran muchas técnicas de la topología y la geometría algebraica, ramas de las matemáticas que se enfocan en lo que les sucede a las formas cuando se deforman, encogen, estiran o cambian sin discontinuidad. "Henri Poincaré esencialmente inventó la topología y dijo claramente que lo hizo para comprender las funciones algebraicas", dijo Farb. "En ese momento, la gente estaba teniendo dificultades para estudiar estas conexiones fundamentales".
El mismo Hilbert reveló una conexión particularmente interesante al aplicar la geometría a este problema. Cuando elaboró su lista de problemas en 1900, los matemáticos ya tenían muchos trucos para reducir los grados de los polinomios, pero todavía no podían avanzar más. Sin embargo, en 1927, Hilbert describió un nuevo truco. Comenzó identificando todas las formas posibles de simplificar polinomios de noveno grado y encontró entre ellas una familia de superficies cúbicas especiales.
Hilbert ya sabía que en cada superficie cúbica lisa, una figura intrincada descrita por un polinomio de tercer grado, hay exactamente 27 líneas, sin importar cuán retorcidas parezcan. Estas líneas rectas cambian a medida que cambian los coeficientes de los polinomios. Se dio cuenta de que conociendo la posición de uno de ellos, puede simplificar el polinomio de noveno grado y encontrar sus raíces. La fórmula requería solo cuatro parámetros; en términos modernos, esto significaba que el grado de resolución no excedía de 4.
"La asombrosa idea de Hilbert fue que este milagro de la geometría, originado en un mundo completamente diferente, podría usarse para reducir el grado de el resolutivo a 4 ", dijo Farb.
Avanzando hacia una red de conexiones
Cuando Kissin ayudó a Farb y Wolfson a comprender el problema, se dieron cuenta de que la opinión generalmente aceptada de que el problema número 13 de Hilbert estaba resuelto había matado todo interés en el enfoque geométrico hasta el grado de resolución. En enero de 2020, Wolfson publicó un artículo que revitalizó este enfoque. Extendió la inversión geométrica de Hilbert de polinomios de noveno grado a una teoría más general.
Hilbert se concentró en superficies cúbicas para encontrar soluciones a polinomios de noveno grado que contienen solo una variable. Pero, ¿qué pasa con los polinomios de grado superior? Para resolver este problema de manera similar, pensó Wolfson, se podría reemplazar la superficie cúbica con algún tipo de "hipersuperficie" de orden superior formada por estos polinomios de orden superior en muchas variables. La geometría de tales superficies no se comprende bien, pero durante las últimas décadas, los matemáticos han demostrado que en algunos casos siempre se pueden encontrar líneas rectas en ellas.
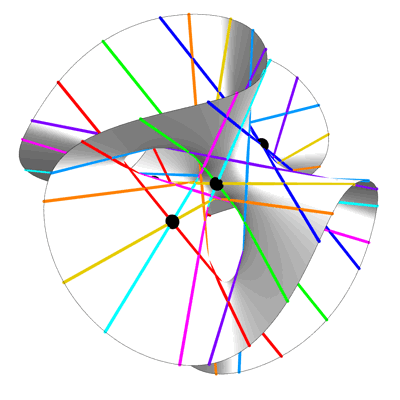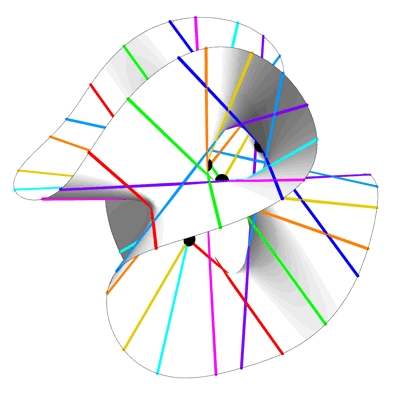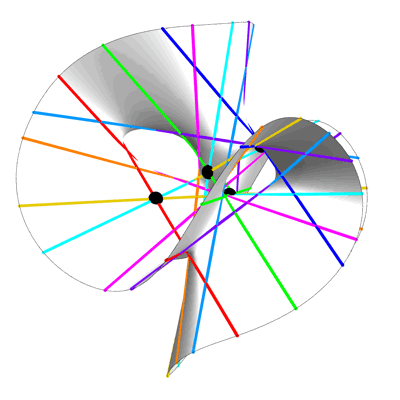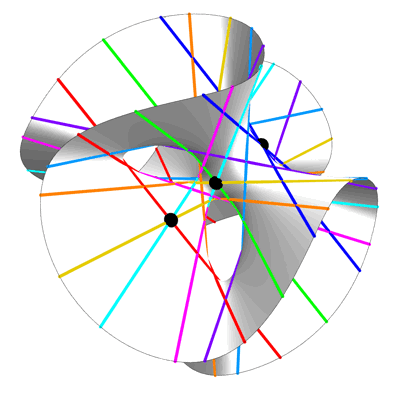
, , , 27 . . , «» .
La idea de Hilbert de usar líneas rectas en una superficie cúbica se puede desarrollar en líneas rectas en estas "hipersuperficies" de grados superiores. Wolfson usó este método para encontrar fórmulas nuevas y más simples para polinomios de ciertos grados. Resulta que incluso si no imagina un polinomio de grado 100, puede encontrar sus raíces "simplemente" encontrando un plano en una hipersuperficie cúbica multidimensional (en este caso, tendrá 47 dimensiones).
Usando este nuevo método, Wolfson confirmó el valor del grado resolutivo encontrado por Hilbert para polinomios de noveno grado. Y para polinomios de algunos otros grados, en particular, grados por encima de 9, su método reduce el rango de valores posibles del grado de resolutivo.
Así que este no es un ataque directo al decimotercer problema de Hilbert, sino un enfoque de los polinomios en general. "Encontraron algunas preguntas relacionadas y pudieron avanzar en ellas, con la esperanza de que esto arrojara luz sobre la pregunta original", dijo McMullen. Y su trabajo indica nuevas formas de trabajar con estos constructos matemáticos.
La teoría general del grado de resolutivo también muestra que las conjeturas de Hilbert sobre ecuaciones de sexto, séptimo y octavo orden son equivalentes a otros problemas conocidos en áreas aparentemente no relacionadas de las matemáticas. El grado de resolución, según Farb, ofrece una forma de organizar estos problemas en términos de complejidad algebraica, en lugar de agruparlos en clases de complejidad.
Y aunque la teoría se originó a partir del decimotercer problema de Hilbert, los matemáticos no están seguros de que pueda resolver la pregunta abierta sobre los polinomios de séptimo grado. Toca escalas matemáticas gigantescas e inexploradas en dimensiones inimaginables, pero en valores menores de los grados encuentra obstáculos insuperables y es incapaz de determinar los grados de resolución para ellos.
Para McMullen, la falta de progreso, a pesar de los indicios de progreso, es interesante en sí misma. De esto se deduce que el problema contiene secretos que las matemáticas modernas simplemente no pueden comprender. “No pudimos abordar este problema fundamental, significa que no entramos en áreas oscuras”, dijo.
“Se necesitarán ideas completamente nuevas para resolverlo”, dijo Reichstein, quien desarrolló su propia idea para simplificar polinomios, un concepto que él llama “dimensión básica”. "Es imposible predecir de dónde vendrán".
Pero la trinidad no se rinde. "No me voy a rendir", dijo Farb. “Esta tarea definitivamente se ha convertido en mi ballena blanca . Ella hace que no me detenga en esta red de conexiones y las matemáticas que la rodean ".