
En un artículo publicado recientemente en Physical Review Research, demostramos cómo el aprendizaje profundo simplifica la solución de ecuaciones mecánicas cuánticas fundamentales para sistemas reales. Al mismo tiempo, no solo se resuelve una cuestión científica fundamental, sino que también se abren perspectivas para el uso práctico de los resultados obtenidos en el futuro.
Los investigadores podrán crear prototipos de nuevos materiales y compuestos in silico antes de intentar sintetizarlos en el laboratorio. También publicó el códigode este estudio; por lo tanto, los equipos de física y química computacional pueden basarse en su trabajo y aplicarlo a una variedad de problemas. Como parte del estudio, se desarrolló una nueva arquitectura de red neuronal, Fermionic Neural Network o FermiNet, que es muy adecuada para simular el estado cuántico de grandes colecciones de electrones, y todos los enlaces químicos se basan en electrones. FermiNet demostró por primera vez cómo utilizar el aprendizaje profundo para calcular la energía de átomos y moléculas desde cero. El modelo resultante resultó ser lo suficientemente preciso para su aplicación práctica y, en el momento de la publicación del artículo original (octubre de 2020), seguía siendo el método de red neuronal más preciso utilizado en la industria. Es asumidoque los métodos y herramientas asociados pueden ser útiles para resolver problemas fundamentales en las ciencias naturales. Los autores de FermiNet ya lo están utilizando en su trabajo sobre la convolución de proteínas , la dinámica de compuestos vítreos , la cromodinámica cuántica en una red y en muchos otros proyectos que ayudan a traducir estos desarrollos en la práctica.
Una breve historia de la mecánica cuántica
Al mencionar la "mecánica cuántica", es probable que confunda al interlocutor con este tema como ningún otro. Inmediatamente recuerdo imágenes como el gato de Schrödinger, que paradójicamente puede estar vivo y muerto al mismo tiempo, así como partículas elementales que son tanto corpúsculos como ondas. En un sistema cuántico, una partícula como un electrón no tiene una ubicación específica, a diferencia de la situación en la física clásica. En física cuántica, la posición de un electrón se describe mediante una nube de probabilidades, es decir, se extiende sobre todos esos puntos, en cada uno de los cuales puede aparecer un electrón. Debido a este absurdo estado de cosas, Richard Feynman encontró posible afirmar: "Creo que puedo decir con seguridad que nadie comprende la mecánica cuántica".
A pesar de toda esta extraña rareza, la esencia de la teoría se puede expresar en solo unas pocas ecuaciones ordenadas. La más famosa de ellas, la ecuación de Schrödinger, describe el comportamiento de las partículas en una escala cuántica de la misma manera que las ecuaciones de Newton describen el comportamiento de los cuerpos en las escalas macroscópicas más familiares. Si bien la interpretación de esta ecuación obligará a cualquiera a agarrarse la cabeza, su componente matemático es mucho más fácil de usar en la práctica, por lo que nació el célebre profesor "cállate y cuenta", con el que lucharon contra las incómodas preguntas filosóficas de los estudiantes.
Estas ecuaciones son suficientes para describir el comportamiento de toda la materia que nos es familiar a nivel de átomos y núcleos. Un componente ilógico de la mecánica cuántica subyace a todo tipo de fenómenos exóticos: la superconductividad, la superfluidez, el láser y los semiconductores solo son posibles debido a los efectos cuánticos. Pero incluso algo tan modesto como un enlace covalente, el componente básico de toda la química, es el resultado de interacciones cuánticas de electrones. Cuando finalmente se elaboraron estas reglas en la década de 1920, los científicos se dieron cuenta de que por primera vez se había creado una teoría que detallaba el trabajo de toda la química. En principio, las ecuaciones cuánticas podrían simplemente adaptarse para diferentes moléculas, resolverse teniendo en cuenta la energía del sistema y luego determinar qué moléculas serán estables y qué reacciones ocurrirán espontáneamente. Pero,cuando se intentó sentarnos y calcular las soluciones para estas ecuaciones, resultó que esto es factible para el átomo más simple (hidrógeno) y prácticamente no para ningún otro. Todos los demás cálculos resultaron demasiado complicados.
Paul Dirac resumió maravillosamente el vertiginoso optimismo de aquellos días:
Entonces, las leyes físicas básicas requeridas para una teoría matemática que describiría la mayor parte de la física y toda la química ya se conocen. El problema es que, en la práctica, la aplicación de estas leyes da ecuaciones demasiado complejas, que objetivamente somos incapaces de resolver. Por tanto, parece deseable desarrollar métodos aproximados para la aplicación práctica de la mecánica cuántica.
1929
Muchos aceptaron el llamado de Dirac y pronto los físicos comenzaron a desarrollar métodos matemáticos que permitirían aproximar el comportamiento de los enlaces moleculares y otros fenómenos químicos a nivel cualitativo. Todo comenzó con una descripción aproximada del comportamiento de los electrones; esta información se estudia en un curso de introducción a la química. Con esta descripción, cada electrón entra en su propio orbital, lo que le permite calcular la probabilidad de que un electrón se encuentre en un punto específico en las proximidades de un núcleo atómico. En este caso, la forma de cada orbital depende de la forma promedio de todos los demás orbitales. Dado que en tal descripción de acuerdo con el modelo de "campo autoconsistente", se supone que cada electrón está unido a un solo orbital, esta imagen transmite de manera muy incompleta las propiedades reales de los electrones. Aun así es suficientepara determinar la energía total de la molécula con un error de solo alrededor del 0,5%.
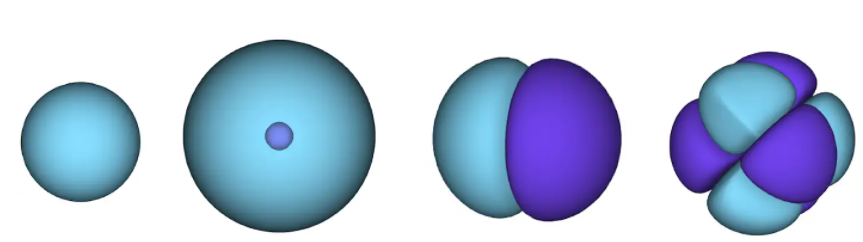
Figura 1 - orbitales atómicos. una superficie es un área en la que es probable que se ubique un electrón. en la región azul la función de onda es positiva y en la violeta es negativa.
Desafortunadamente para el químico practicante, un error del 0.5% es demasiado grande para ser tolerado. La energía de los enlaces moleculares es solo una pequeña fracción de la energía total de un sistema, y la predicción correcta de si una molécula será estable a menudo puede depender de tan solo el 0,001% de la energía total del sistema, o aproximadamente el 0,2%. de la energía de "correlación" restante.
Por ejemplo, mientras que la energía total de los electrones en una molécula de butadieno es es de casi 100.000 kilocalorías por mol, la diferencia de energía entre las diversas configuraciones posibles de la molécula es de sólo 1 kilocaloría por mol. Es decir, si es necesario predecir correctamente la forma natural de la molécula de butadieno, se requiere el mismo nivel de precisión que cuando se mide el ancho de un campo de fútbol con una precisión de un milímetro.
Con la proliferación de la computación electrónica poco después de la Segunda Guerra Mundial, los científicos desarrollaron una gran cantidad de métodos computacionales que no podrían describirse como campos autoconsistentes. Estos métodos están indicados por un montón inimaginable de abreviaturas que cubren todo el alfabeto, pero cada uno de estos métodos contiene algún tipo de compensación entre precisión y eficiencia. En un extremo se encuentran los métodos que son, de hecho, precisos, pero escalan peor que exponencialmente a medida que aumenta el número de electrones, por lo que no son adecuados para trabajar con la mayoría de las moléculas, excepto con las más pequeñas. En el otro extremo, hay métodos que escalan linealmente pero no son muy precisos. Estos métodos computacionales han tenido un impacto tremendo en la química práctica: el Premio Nobel de Química de 1998 fue otorgado a los autores de muchos de estos algoritmos.
A pesar de la amplitud de las herramientas mecánicas cuánticas computacionales existentes, el problema de representar información de manera eficiente requirió el desarrollo de un nuevo método. No es una coincidencia que solo decenas de miles de electrones estén involucrados en los cálculos químicos cuánticos modernos más grandes (estamos hablando de los métodos más aproximados), mientras que los métodos clásicos de cálculos químicos, por ejemplo, la dinámica molecular, permiten manejar millones de átomos. No es difícil describir el estado de un sistema clásico; solo necesita rastrear la posición y el impulso de cada partícula. Imaginar el estado de un sistema cuántico es un desafío mucho mayor. Tenemos que asignar un valor probabilístico a cada posible configuración de posiciones de electrones. Esta información está codificada en una función de onda,lo que le permite asignar un número positivo o negativo a cada configuración electrónica, y la función de onda cuadrada da la probabilidad con la que el sistema se puede encontrar en dicha configuración. El espacio de todas las configuraciones posibles es colosal: si intentara imaginarlo como una cuadrícula con 100 puntos en cada dimensión, entonces el número de posibles configuraciones de electrones para un átomo de silicio sería mayor que el número de átomos en el universo.
Aquí es donde las redes neuronales profundas resultan útiles. En los últimos años, se han realizado tremendos avances en la representación de distribuciones de probabilidad complejas con alta dimensionalidad utilizando redes neuronales. Ahora se sabe cómo entrenar eficazmente dichas redes con la expectativa de su escalabilidad. Sugerimos que dado que estas redes ya han demostrado su agilidad en el entrenamiento de funciones con muchas dimensiones en la resolución de problemas del campo de la inteligencia artificial, quizás sirvan para representar funciones de onda cuántica. No fuimos los primeros en tener tales pensamientos, otros investigadores, en particular, Giuseppe Carleo y Matthias Troyer.demostró cómo el aprendizaje profundo moderno es aplicable a la resolución de problemas cuánticos idealizados. Queríamos utilizar redes neuronales para abordar problemas más realistas en química y física del estado sólido, lo que significaba que necesitábamos tener en cuenta los electrones en nuestros cálculos.
Solo hay una advertencia cuando se trabaja con electrones. Los electrones deben obedecer el principio de exclusión de Pauli, es decir, dos electrones no pueden estar simultáneamente en el mismo lugar. El caso es que los electrones son partículas elementales de entre los fermiones que componen la mayoría de los primeros ladrillos de materia, en particular, protones, neutrones, quarks, neutrinos, etc. Su función de onda debe ser antisimétrica: si intercambias dos electrones, la función de onda se multiplica por -1. Por lo tanto, existe una probabilidad cero de que dos electrones se coloquen uno encima del otro, ya que la probabilidad de esto (y la función de onda correspondiente) es igual a cero.
Por tanto, era necesario desarrollar una red neuronal de nuevo tipo, que fuera antisimétrica con respecto a la entrada que entraba. Lo llamamos Fermionic Neural Network o FermiNet. En la mayoría de los métodos de química cuántica, la antisimetría se introduce mediante una función llamada determinante. El determinante es una matriz que tiene la siguiente propiedad: si intercambia dos de sus filas, la salida se multiplica por -1, exactamente como la función de onda de los fermiones. Puede tomar un montón de funciones de un electrón, calcularlas para cada electrón en su sistema y luego ajustar todos los resultados en una matriz. En este caso, el determinante de la matriz será una función de onda verdaderamente antisimétrica. La principal limitación de este enfoque es que la función resultante, denominada determinante de Slater, no es de aplicación generalizada.Las funciones de onda de los sistemas reales suelen ser mucho más complejas. Por lo general, se toman grandes combinaciones lineales de determinantes de Slater, a veces millones o más, para corregir este problema, y luego se realizan algunas correcciones simples basadas en pares de electrones. Incluso entonces, es posible que el sistema no sea lo suficientemente preciso para calcular las energías.

2 – . – , 1. 1 2 , , -1. .
Las redes neuronales profundas suelen ser muy superiores en eficiencia a las combinaciones lineales de funciones básicas cuando se representan funciones complejas. En FermiNet, esta superioridad se logra al introducir cada una de las funciones en el determinante, la función de todos los electrones. Este método es mucho más poderoso que usar funciones de uno y dos electrones. FermiNet proporciona un flujo de información independiente para cada electrón. Sin tener en cuenta las interacciones entre estos flujos, la red no sería más expresiva que el determinante Slater habitual. Para hacer más, promediamos la información recopilada de todos los flujos en cada una de las capas de la red y pasamos esta información a cada uno de los flujos a la siguiente capa. Por consiguiente, dichos flujos tienen propiedades de simetría adecuadas para crear una función antisimétrica.
La información sobre cada una de las capas en las redes neuronales de gráficos se agrega de manera similar . A diferencia de los determinantes de Slater, las redes FermiNet son aproximadores de funciones universales , al menos siempre que las capas de redes neuronales sigan siendo lo suficientemente amplias. Esto significa que si podemos entrenar estas redes correctamente, entonces pueden producir una solución casi exacta a la ecuación de Schrödinger.
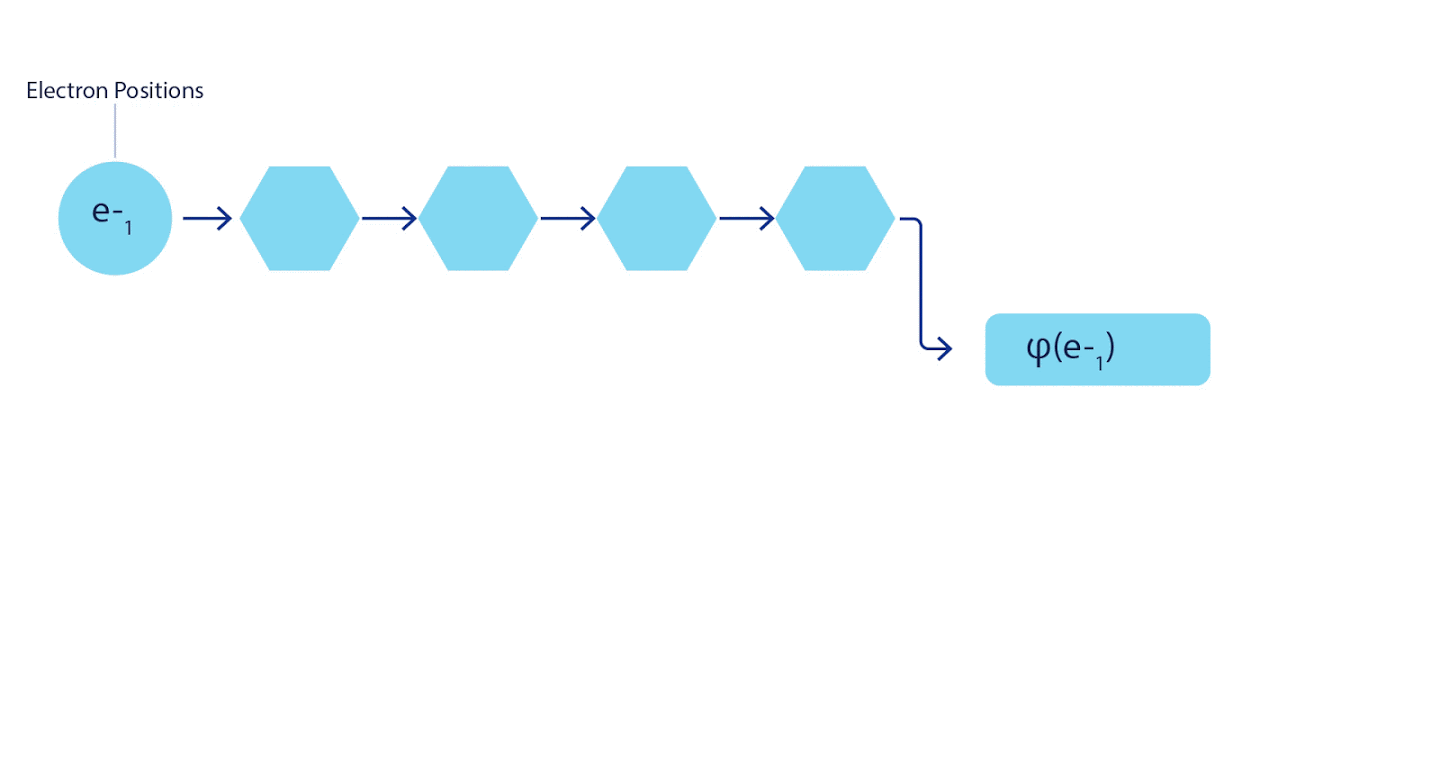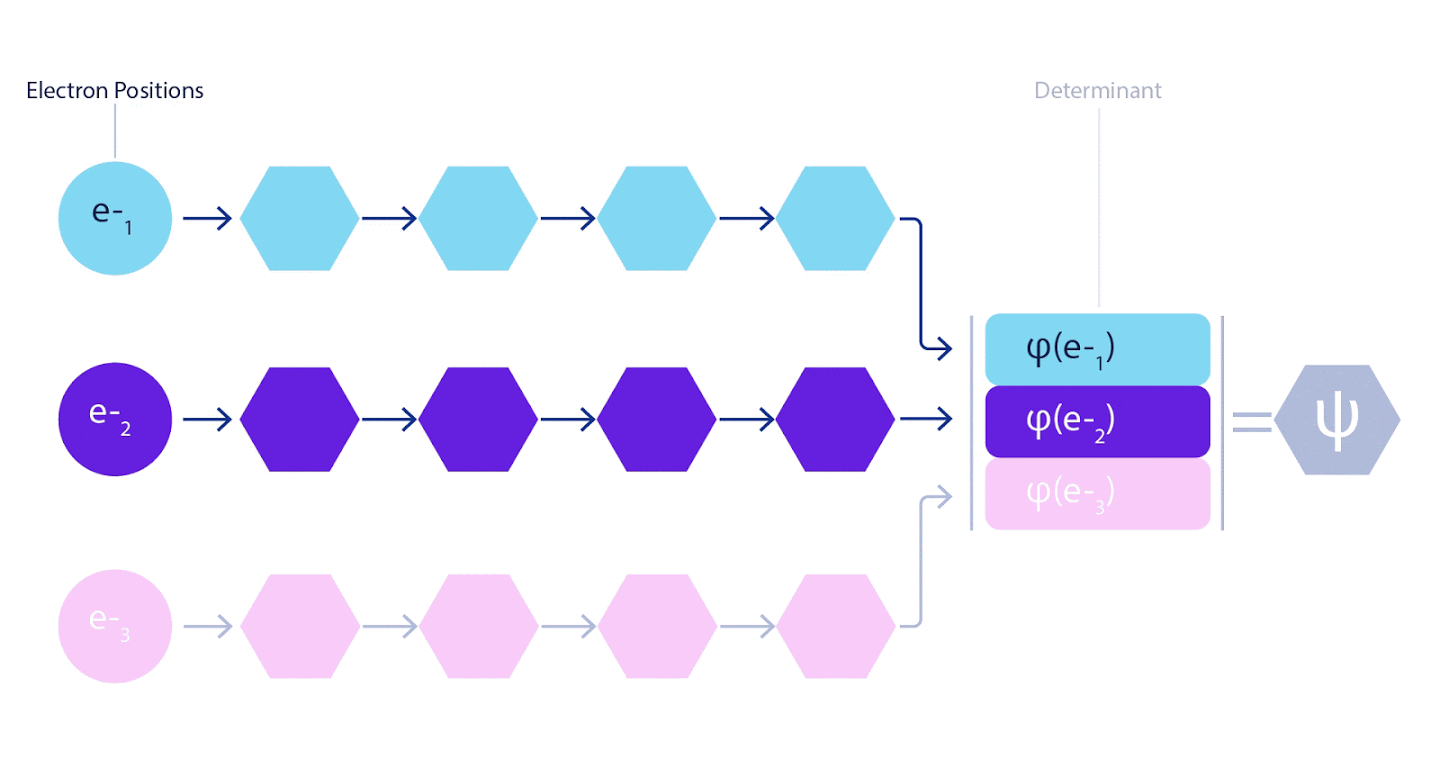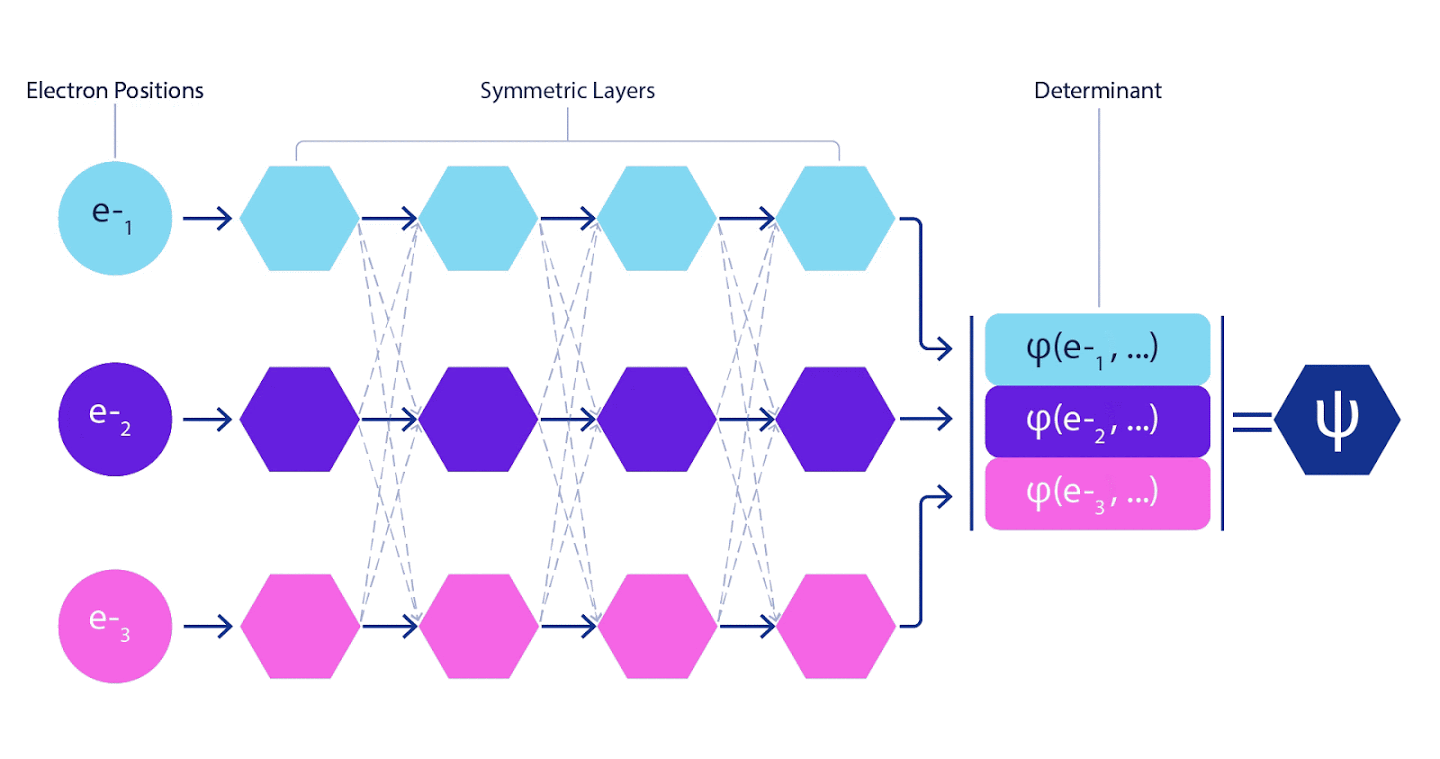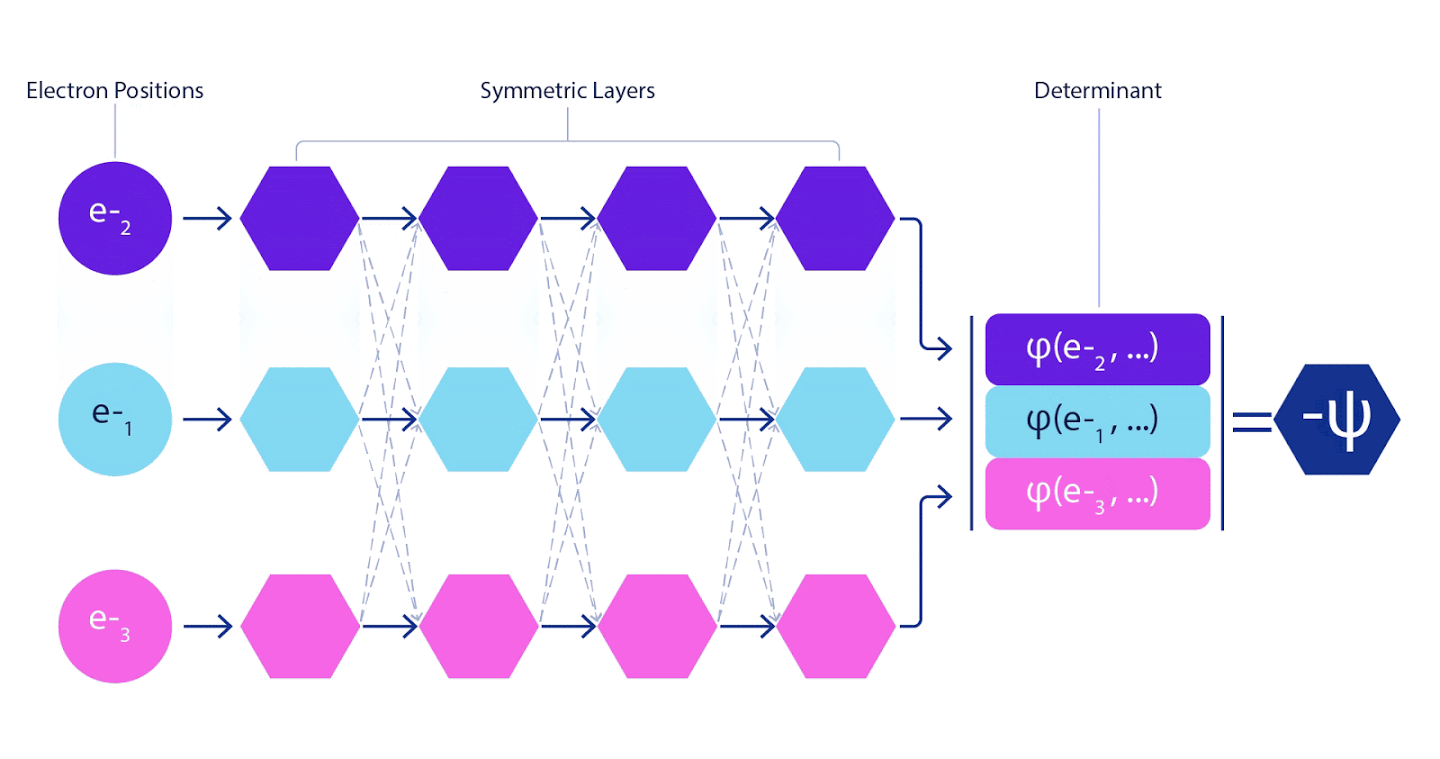
3 – FermiNet. (, ) . FermiNet , , , . , - -1.
Personalizamos la red FermiNet, minimizando la energía del sistema. Para hacer esto con precisión, necesitaríamos calcular la función de onda en todas las configuraciones posibles de electrones, por lo que tendríamos que hacer esto aproximadamente. Por lo tanto, tomamos una muestra aleatoria de configuraciones de electrones, calculamos la energía localmente para cada variante de ordenamiento de electrones y minimizamos esta energía, no la verdadera. Este método se llama "Monte Carlo" porque es un poco como las acciones de un jugador de casino que lanza los dados una y otra vez. Dado que la función de onda cuadrada hace posible observar alguna configuración de partículas en cualquier ubicación, es más conveniente generar muestras de la función de onda en sí, en esencia, simulando el acto de observar partículas.
Si bien la mayoría de las redes neuronales se entrenan con algunos datos externos, en nuestro caso, la red neuronal en sí genera la entrada que entra en ella para el entrenamiento. La situación es un poco como sacarte de un pantano agarrándote del pelo y significa que no necesitamos ningún dato de entrenamiento más que las posiciones de esos núcleos atómicos alrededor de los cuales bailan los electrones. La idea básica, conocida como el Método de Monte Carlo Cuántico Variacional (o VMC para abreviar), ha existido en la ciencia desde la década de 1960 y generalmente se considera una forma barata pero no muy precisa de calcular la energía de un sistema. Al reemplazar funciones de onda simples basadas en determinantes de Slater con funciones de FermiNet, logramos mejorar radicalmente la precisión de este enfoque en todos los sistemas que consideramos.
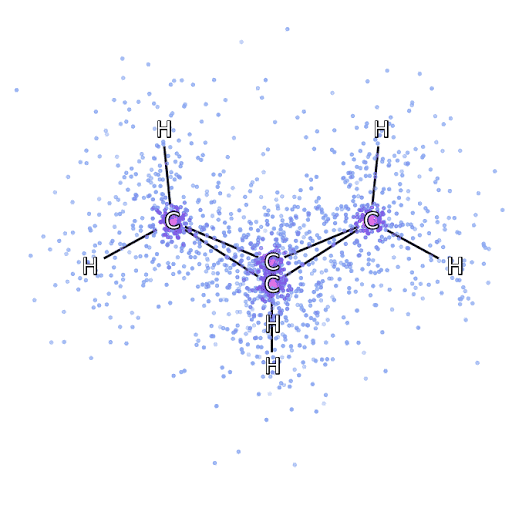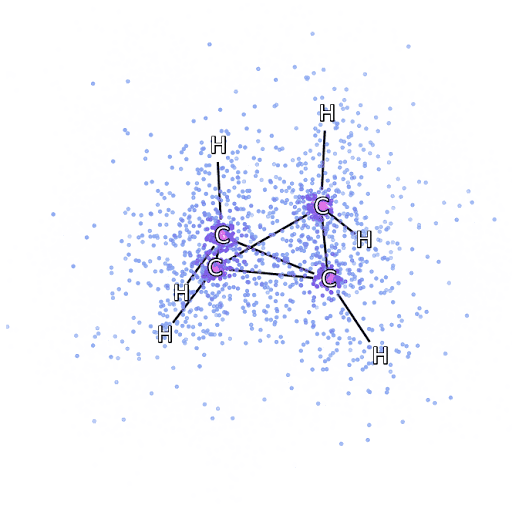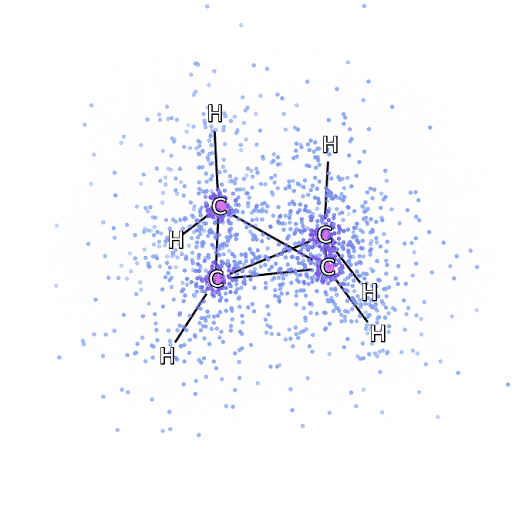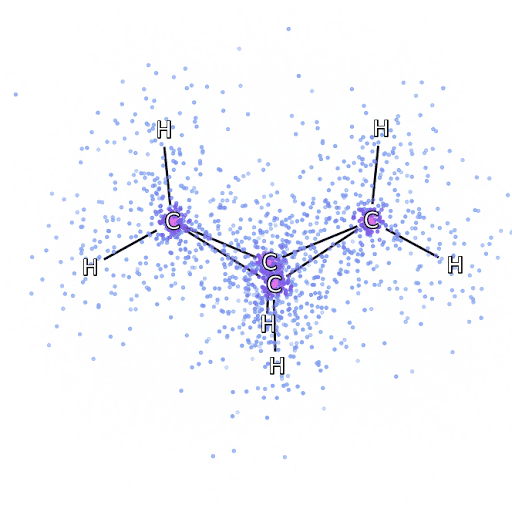
4 – , FermiNet, .
Para asegurarnos de que FermiNet sea realmente un gran avance en su área temática, comenzamos examinando sistemas simples y bien estudiados, por ejemplo, los átomos de la primera fila de la tabla periódica (desde el hidrógeno hasta el neón). Estos son sistemas pequeños, de 10 electrones o menos, por lo que se prestan a la investigación utilizando los métodos más precisos (pero exponencialmente más complejos). FermiNet supera con creces los cálculos VMC comparables y, a menudo, puede reducir el error a la mitad o más en comparación con los cálculos escalables exponencialmente. En sistemas más grandes, los métodos que se vuelven más complejos exponencialmente se vuelven inaplicables, por lo que usamos el método de clúster acoplado como referencia. Este método funciona bien en moléculas con configuraciones estables, pero se resbala cuando los enlaces se estiran o dañan.y estos factores son fundamentales para comprender las reacciones químicas. Si bien escala mucho mejor que exponencialmente, el método de clúster conectado utilizado en este estudio aún funciona lo mejor posible con moléculas de tamaño mediano. Aplicamos FermiNet a moléculas cada vez más grandes, desde hidruro de litio hasta biciclobutano; fue el sistema más grande que analizamos, con 30 electrones. En las moléculas más pequeñas, FermiNet capturó una asombrosa diferencia del 99,8% entre la energía de los cúmulos unidos y la energía derivada de un solo determinante de Slater. En el caso del biciclobutano, FermiNet todavía capturó el 97% o más de esta energía de correlación, un gran logro para un enfoque supuestamente "barato pero impreciso".Si bien escala mucho mejor que exponencialmente, el método de clúster conectado utilizado en este estudio aún funciona lo mejor posible con moléculas de tamaño mediano. Aplicamos FermiNet a moléculas cada vez más grandes, desde hidruro de litio hasta biciclobutano; fue el sistema más grande que analizamos, con 30 electrones. En las moléculas más pequeñas, FermiNet capturó una asombrosa diferencia del 99,8% entre la energía de los cúmulos unidos y la energía derivada de un solo determinante de Slater. En el caso del biciclobutano, FermiNet todavía capturó el 97% o más de esta energía de correlación, un gran logro para un enfoque supuestamente "barato pero impreciso".Si bien escala mucho mejor que exponencialmente, el método de clúster conectado utilizado en este estudio aún funciona lo mejor posible con moléculas de tamaño mediano. Aplicamos FermiNet a moléculas cada vez más grandes, desde hidruro de litio hasta biciclobutano; fue el sistema más grande que analizamos, con 30 electrones. En las moléculas más pequeñas, FermiNet capturó una asombrosa diferencia del 99,8% entre la energía de los cúmulos unidos y la energía derivada de un solo determinante de Slater. En el caso del biciclobutano, FermiNet todavía capturó el 97% o más de esta energía de correlación, un gran logro para un enfoque supuestamente "barato pero impreciso".que se aplicó en el estudio descrito, todos trabajan igualmente como máximo con moléculas de tamaño medio. Aplicamos FermiNet a moléculas cada vez más grandes, desde hidruro de litio hasta biciclobutano; fue el sistema más grande que analizamos, con 30 electrones. En las moléculas más pequeñas, FermiNet capturó una asombrosa diferencia del 99,8% entre la energía de los cúmulos unidos y la energía derivada de un solo determinante de Slater. En el caso del biciclobutano, FermiNet todavía capturó el 97% o más de esta energía de correlación, un gran logro para un enfoque supuestamente "barato pero impreciso".que se aplicó en el estudio descrito, todos trabajan igualmente como máximo con moléculas de tamaño medio. Aplicamos FermiNet a moléculas cada vez más grandes, desde hidruro de litio hasta biciclobutano; fue el sistema más grande que analizamos, con 30 electrones. En las moléculas más pequeñas, FermiNet capturó una asombrosa diferencia del 99,8% entre la energía de los cúmulos unidos y la energía derivada de un solo determinante de Slater. En el caso del biciclobutano, FermiNet todavía capturó el 97% o más de esta energía de correlación, un gran logro para un enfoque supuestamente "barato pero impreciso".comenzando con hidruro de litio y llegando al biciclobutano, fue el sistema más grande que consideramos, tiene 30 electrones. En las moléculas más pequeñas, FermiNet capturó una asombrosa diferencia del 99,8% entre la energía de los cúmulos unidos y la energía derivada de un solo determinante de Slater. En el caso del biciclobutano, FermiNet todavía capturó el 97% o más de esta energía de correlación, un gran logro para un enfoque supuestamente "barato pero impreciso".desde hidruro de litio hasta biciclobutano: fue el sistema más grande que consideramos, tiene 30 electrones. En las moléculas más pequeñas, FermiNet capturó una asombrosa diferencia del 99,8% entre la energía de los cúmulos unidos y la energía derivada de un solo determinante de Slater. En el caso del biciclobutano, FermiNet todavía capturó el 97% o más de esta energía de correlación, un gran logro para un enfoque supuestamente "barato pero impreciso".enfoque "impreciso".enfoque "impreciso".

La Figura 5 es una representación gráfica de la fracción de la energía de correlación que FermiNet captura correctamente cuando trabaja con moléculas. La barra violeta marca un 99% de energía de correlación. De izquierda a derecha: hidruro de litio, nitrógeno, etileno, ozono, etanol y biciclobutano.
Si bien los métodos de agrupamiento acoplados funcionan bien con moléculas estables, la verdadera "vanguardia" de la química computacional tiene que ver con comprender cómo las moléculas se estiran, retuercen y rompen. Al resolver tales problemas, los métodos de clúster conectados a menudo fallan, por lo que debe comparar el resultado con tantas muestras de control como sea posible para asegurarse de que la respuesta sea coherente. En el marco del experimento descrito, se consideraron dos sistemas de control estirado: una molécula de nitrógeno (N 2) y una cadena de hidrógeno de 10 átomos (H 10 ). En la molécula de nitrógeno, el enlace es especialmente complejo, ya que en él participan 3 electrones de cada átomo.
La cadena de hidrógeno, a su vez, es interesante para comprender qué propiedades exhiben los electrones en los materiales , por ejemplo, para predecir si un material dado conducirá electricidad o no. En ambos sistemas, el método de conglomerados conectados funcionó bien en equilibrio, pero tuvo dificultades cuando se estiraron los enlaces. Los métodos tradicionales de VMC no funcionaron bien en toda la gama de ejemplos. Pero FermiNet resultó ser uno de los mejores métodos de todos los investigados, independientemente de la longitud del enlace.
Conclusión
Creemos que FermiNet es el comienzo de grandes avances en la síntesis de métodos de aprendizaje profundo y química cuántica computacional. La mayoría de los sistemas con los que se ha revisado FermiNet hasta ahora se comprenden y comprenden bien. Pero así como los primeros buenos resultados utilizando el aprendizaje profundo en otros dominios han estimulado un aumento en la investigación adicional y un progreso rápido, es de esperar que suceda lo mismo con FermiNet, y surgirán ideas para arquitecturas de redes neuronales nuevas e incluso mejores. Ya después de que el trabajo descrito fuera publicado en arXiv, otros gruposcompartió sus enfoques para aplicar el aprendizaje profundo a la resolución de problemas que involucran muchos electrones. Además, apenas hemos profundizado en la física cuántica computacional y planeamos utilizar FermiNet para resolver problemas complejos en el campo de la ciencia de los materiales y la física del estado sólido.
El artículo científico está aquí y el código se puede ver aquí . Los autores desean agradecer a Jim Kinwin, Adam Kine y Dominic Barlow por su ayuda en la preparación de los dibujos.