Cómo cuatro matemáticos resolvieron la cuestión de las formas geométricas básicas creando una lista completa de tetraedros con ángulos racionales utilizando métodos de teoría de números.
Los 59 tetraedros con ángulos diedros racionales pueden verse desde diferentes lados como referencia .
El tetraedro es la forma tridimensional más simple con lados planos. Sus principales propiedades han desconcertado a las mentes inquisitivas incluso en los días de Platón y Aristóteles. Y en noviembre de 2020, se publicó la prueba final , que identificó de manera confiable todos los tetraedros especiales existentes. En este trabajo, los matemáticos están respondiendo a la pregunta de una figura antigua gracias a tecnologías avanzadas que permiten utilizar un nuevo método para encontrar soluciones a ciertas ecuaciones.
“Estos son objetos matemáticos idealizados que siempre estarán con nosotros, y ahora los conocemos todos”, dice Martin Weissman de la Universidad de California, Santa Cruz.
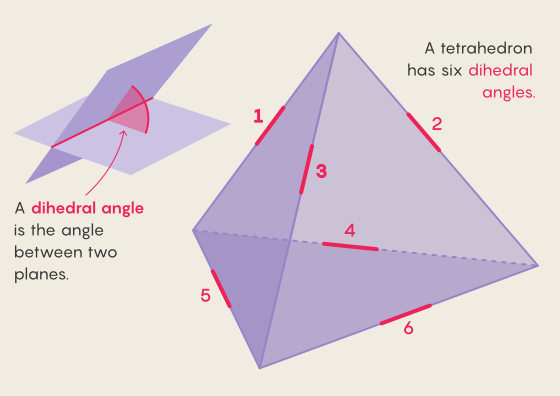
El tetraedro tiene una base triangular y tres lados triangulares, formando una pirámide. Pares de caras se tocan a lo largo de los bordes para formar seis esquinas diedras.
La nueva demostración define todas las variantes de la configuración del tetraedro, donde cada uno de los seis ángulos diedros tiene valores racionales, lo que significa que cada uno de ellos se puede escribir como una fracción. Afirma que hay exactamente 59 ejemplos separados, así como 2 familias infinitas de tetraedros, que satisfacen esta condición.
De hecho, estos tetraedros fueron descubiertos por los matemáticos hace décadas utilizando métodos de búsqueda por computadora, pero no sabían si había alguno más. En términos más generales, no entendieron cómo probar que no había otros tetraedros similares.
"Fueron encontrados en la década de 1990, pero no fue hasta 2020 que pudimos demostrar que la lista era completa", dijo Kiran Kedlaya , matemático de la Universidad de California en San Diego. Kedlaya es coautor de la prueba con Alexander Kolpakov de la Universidad de Neuchâtel en Suiza, Bjorn Punen del Instituto de Tecnología de Massachusetts y Michael Rubinstein.de la Universidad de Waterloo.
Samuel Velasco / Quanta Magazine
El problema de clasificar tetraedros con ángulos diedros racionales puede parecer simple, pero se necesitaron años de conocimiento matemático acumulado para resolverlo, así como una potencia de cálculo que no estaba disponible ni siquiera hace diez años.
“No se puede obtener ese tipo de resultado simplemente jugando con un lápiz y papel. Han desarrollado métodos muy sofisticados ”, dice Marjorie Seneschal de Smith College.
Casi no hay dibujos en la prueba de 30 páginas. En cambio, la lógica se basa en resolver una ecuación polinómica en la que los coeficientes y las variables se elevan a una potencia, por ejemplo, y = 3x 2+ 6. Por supuesto, la ecuación considerada en la demostración es mucho más complicada.
"La mayor parte del trabajo se basa en la teoría de números, pero la geometría se encuentra en la superficie", dice Kedlaya.
La conexión entre la geometría y la teoría de números les dio a los matemáticos una pista, pero tuvieron que trabajar duro para desarrollar esta idea, porque es muy difícil encontrar soluciones especiales a ecuaciones complejas y demostrar que las encontraste todas. Los matemáticos no saben cómo hacer esto para la mayoría de las ecuaciones.
“No existe un método único que funcione siempre. Casi nunca se puede resolver una ecuación ”, dice Peter Sarnak del Instituto de Estudios Avanzados.
¡Solo en este caso, los matemáticos tuvieron éxito! Al descubrir un nuevo método para encontrar soluciones a ecuaciones polinomiales, respondieron la pregunta básica sobre las formas geométricas y pueden haber facilitado la búsqueda de soluciones a otras ecuaciones en el futuro.
Prueba de tetraedros
La cuestión de definir todos los tetraedros con ángulos diedros racionales (tetraedros racionales) fue formulada formalmente por primera vez por John Conway y Antonia Jones en un artículo de 1976.
Querían encontrar tetraedros que pudieran cortarse y ensamblarse en un cubo del mismo volumen, una propiedad conocida como congruencia de tijera. En su trabajo, desarrollaron razonamientos que se remontan a 1900, cuando David Hilbert propuso 23 problemas que guiaron la investigación matemática en el siglo XX. Su tercer problema está relacionado con la siguiente pregunta: son pares de figuras tridimensionales de tijeras de igual volumen. Pronto se demostró que este no era el caso, pero resultó que todos los tetraedros racionales son congruentes con el cubo.
“Conway y Jones plantearon la cuestión de los tetraedros racionales como un caso especial de una cuestión mucho más compleja de clasificación de tetraedros”, dijo Kedlaya.
Estos son objetos matemáticos idealizados que siempre estarán con nosotros.
Martin Weissman, Universidad de California, Santa Cruz.
Pudieron esbozar un método para encontrar estos tetraedros: resolver una ecuación polinomial específica. Su ecuación contiene seis variables correspondientes a los seis ángulos diedros del tetraedro y tiene 105 términos que reflejan la compleja relación de los ángulos diedros del tetraedro entre sí. A modo de comparación, imagine un triángulo, sus tres ángulos interiores están conectados dentro de un polinomio simple, que consta de solo tres miembros: a + b + c = 180 grados.
La ecuación polinómica identificada por Conway y Jones también tiene infinitas soluciones que corresponden a configuraciones infinitas de posibles tetraedros. Conway y Jones dijeron que para definir tetraedros con todos los ángulos diedros racionales, los matemáticos necesitan encontrar una clase especial de soluciones a la ecuación que correspondan exactamente a los tetraedros racionales.
Ellos mismos no sabían cómo encontrar una solución, pero estaban seguros de que se podía hacer: "Es probable que un tetraedro ordinario ... cuyos ángulos diedros sean racionales, se pueda encontrar usando nuestros métodos".
Más de 40 años después, cuatro matemáticos han confirmado su suposición.
Raíces de uno
La estrategia de Conway y Jones es bastante común entre los matemáticos que a menudo buscan tipos especiales de soluciones cuando estudian ecuaciones polinomiales. Pueden ser soluciones en forma de números enteros o racionales. O, como en este caso, pueden ser soluciones con el elegante nombre de “raíces de uno”.
La mayoría de las raíces de uno no aparecen en la recta numérica normal. En cambio, se encuentran entre números complejos como 3 + 4i, que tienen una parte real (3) y una parte imaginaria (4). Las raíces de la unidad sirven como soluciones a las ecuaciones polinomiales y tienen una propiedad algebraica especial: elevarlas a una determinada potencia da 1. Además, tienen una elegante representación geométrica: todas se encuentran en el círculo unitario en el plano complejo.
Para resolver la ecuación polinomial de Conway-Jones, debe asignar números complejos a las seis variables para que la ecuación de 105 términos sea verdadera. Las variables no representan literalmente las medidas reales de los ángulos, sino que reemplazan los números complejos asociados con los cosenos de los ángulos. Conway y Jones notaron que los tetraedros racionales corresponderán a soluciones de un polinomio en el que todas las variables son raíces de unidad.
"Seis ángulos se convierten en seis puntos en el círculo unitario, y estos números complejos son necesarios para satisfacer la ecuación polinomial", dijo Weissman.

Samuel Velasco / Revista Quanta
Sin embargo, conocer esta correspondencia no es tan útil como podría parecer. Encontrar soluciones es una cosa. Y demostrar que los ha encontrado a todos es una tarea completamente diferente y mucho más difícil.
En 1995, dos autores de un nuevo trabajo, Punen y Rubinstein, encontraron todos los tetraedros con ángulos diedros racionales, como resultó al final. De hecho, adivinaron la forma de encontrarlos sustituyendo combinaciones de seis números racionales en la ecuación.
“Puedes simplemente intentar tomar seis números racionales e insertarlos en la ecuación”, dijo Poonen. “El problema es que solo se pueden encontrar soluciones de esta manera. Pero no deja claro si se han encontrado todas las opciones posibles ".
Busque todas las soluciones
En su nuevo trabajo, cuatro matemáticos demostraron que la lista de tetraedros con ángulos racionales hallada por Punen y Rubinstein hace 25 años estaba completa y no se descubrirían otros ejemplos.
Su colaboración comenzó en marzo de 2020 después de que Poonen escuchara en una charla sobre el trabajo relacionado de Kedlai, en coautoría de otro matemático. Buscaron raíces de la unidad de otro polinomio para resolver otro problema de clasificación. Poonen se dio cuenta de inmediato de que esto tenía algo que ver con su anterior estudio inacabado de los tetraedros.
"Bjorn estaba muy interesado en mi trabajo", dijo Kedlay. “Él dijo, 'Espera, eso es exactamente lo que necesitaba en la década de 1990'.
Bjorn Punen escribió una carta a Kiran Kedlae describiendo el problema de encontrar tetraedros racionales. Su breve carta terminó con una nota optimista. “Llegué bastante lejos en este tema en la década de 1990 [con Michael Rubinstein], y creo que se puede completar con mucho esfuerzo humano y informático.
En 2020, Kiran Kedlaya, Michael Rubinstein, Bjorn Punen y Alexander Kolpakov inventaron una nueva forma de resolver ecuaciones y, al hacerlo, encontraron todos los tetraedros racionales.
Después de esta carta, Kedlai se dirigió a Kolpakov, quien también usó raíces de la unidad para clasificar los tipos de formas geométricas. Al mismo tiempo, Poonen se puso en contacto con su entonces coautor Rubinstein. Habiendo creado un equipo, rápidamente se pusieron a trabajar.
“Organizamos reuniones bastante regulares, probablemente dos horas a la semana durante varios meses”, dijo Kedlaya. Y cuando comenzaron a compilar una lista completa de las raíces de la unidad para el polinomio de Conway-Jones, tenían una idea muy amplia de dónde buscarlas.
Sabían que las soluciones tenían que estar por debajo de un número muy grande, un límite superior. Pero la frontera era tan grande que no era cuestión de explorar todas las posibilidades debajo de ella.
“Estos límites de seis variables son aterradores. Sin ideas fundamentalmente nuevas, la solución a este problema está más allá del ámbito de lo posible ”, dijo Sarnak.
Cuatro matemáticos hicieron que la ecuación se pudiera resolver mediante dos innovaciones importantes.
Primero, bajaron el límite superior. En su nuevo artículo, demostraron que una ecuación polinomial compleja que representa tetraedros puede representarse en sí misma como varios polinomios más simples.
“Estamos pasando de una ecuación con seis variables a un conjunto de cientos de ecuaciones más simples”, dijo Kedlaya.
Demostraron que todas las raíces de unidad de estos polinomios más simples se encuentran por debajo del límite superior, que es mucho más pequeño que el límite superior vasto e inexplorado asociado con un polinomio más complejo. La correspondencia entre ecuaciones más simples y complejas significa que encontrar raíces de una para las primeras resultará en raíces de una para las últimas. Desafortunadamente, incluso este intervalo más pequeño fue demasiado largo para que exploraran todas las opciones posibles.
No puede obtener este resultado simplemente jugando con lápiz y papel.
Marjorie Seneschal, Smith College
La segunda innovación de los autores consistió en el desarrollo de una forma inteligente de búsqueda en este intervalo más reducido. Sabían que las soluciones tienen cierta estructura simétrica, lo que significa que si hay una solución en una parte del intervalo, debe haber una solución en la otra parte del intervalo.
Esto les permitió desarrollar nuevos algoritmos que usaban esta estructura para buscar de manera más eficiente. Además, usaron estos algoritmos en computadoras mucho más poderosas que las que tenían Conway y Jones cuando propusieron por primera vez usar raíces de 1 para resolver un problema.
“Resulta que tuvimos que rediseñar un poco la estrategia [de Conway y Jones] con 40 años de conocimiento adicional y computadoras más poderosas”, dijo Kedlay.
Los nuevos algoritmos probaron todas las combinaciones posibles de soluciones en un intervalo más estrecho. Sobre la base de esta búsqueda exhaustiva y definitiva, los autores finalmente demostraron que solo hay 59 ejemplos separados de tetraedros con ángulos diedros racionales y dos familias infinitas de tetraedros (precisamente los que Punen y Rubinstein habían encontrado décadas antes). Los tetraedros de cada familia infinita difieren en un parámetro, ofreciendo infinitas opciones para aumentar el tamaño de algunos ángulos y disminuir otros, manteniendo todos los ángulos diedros racionales.
En esta exploración, todos encontrarán algo para sí mismos.
Para los matemáticos interesados en identificar las raíces de la unidad de ecuaciones polinomiales, el artículo ofrece una nueva forma conveniente de encontrarlas. En particular, es probable que los métodos utilizados por los autores para reducir un polinomio complejo de Conway-Jones a muchos polinomios más simples se apliquen a otras ecuaciones polinomiales complejas que no se pueden resolver directamente.
"Este trabajo sugiere que muchos otros problemas que parecían insuperables posiblemente podrían resolverse con tales ideas", dijo Sarnak.
Y para aquellos matemáticos y todos los demás a los que les gusta la integridad, el artículo ofrece una respuesta nueva y perfecta: aquí están todos los tetraedros con los que solo puedes soñar.
"Este es un gran logro", dijo Sarnak.