¿Te has preguntado alguna vez cómo sería la vida si la Tierra no fuera una esfera, sino que tuviera una forma diferente? Damos por sentado el buen funcionamiento de nuestro planeta a través del sistema solar y las lentas puestas de sol que podemos disfrutar gracias a la simetría rotacional de la Tierra. Además, la tierra esférica te permite determinar la forma más rápida de llegar del punto A al punto B: simplemente camina en un círculo que pasa por estos dos puntos y corta la esfera por la mitad. Usamos estos caminos más cortos, llamados caminos geodésicos, para planificar rutas de aviones y calcular órbitas de satélites.

Pero, ¿qué pasaría si viviéramos en Cuba? Nuestro mundo se balancearía más, los horizontes son curvos y el camino más corto del punto A al punto B es más difícil de encontrar. Puede que no dediques mucho tiempo a imaginar tu vida en un cubo, pero los matemáticos sí: estudiarán cómo serían nuestros viajes en una variedad de formas. Y la reciente solución a una de las cuestiones fundamentales sobre el dodecaedro cambió por completo la visión del objeto que ha estado ante nuestros ojos durante miles de años.
Encontrar el camino más corto hacia adelante y hacia atrás (desde un punto hasta el mismo punto alrededor del cubo) para un cuerpo geométrico dado puede parecer una tarea sencilla. Después de todo, definitivamente volverá a donde comenzó, ¿verdad?
De hecho, depende de la forma o el cuerpo sobre el que camine. Si se trata de una esfera, entonces sí. (Y sí, estamos omitiendo el hecho de que la Tierra no es una esfera ideal, y su superficie no es completamente lisa). En la esfera, los caminos se repiten a lo largo de una línea recta "círculos grandes", geodésicas, por ejemplo, el ecuador. Si da la vuelta al ecuador, después de aproximadamente 40.000 kilómetros, completará un círculo completo y volverá al punto de partida.
En un mundo cúbico, las líneas geodésicas no son tan obvias. Encontrar un camino recto en una cara es fácil porque cada cara es plana. Pero si estuvieras caminando alrededor del mundo cúbico, ¿cómo seguirías caminando recto cuando llegaste al borde?
Hay un viejo problema matemático divertido que ilustra la respuesta a nuestra pregunta. Imagina una hormiga en una esquina de un cubo que quiere llegar a la esquina opuesta. ¿Cuál es el camino más corto en la superficie de un cubo desde el punto A al punto B?
Imagínese los diferentes caminos que podría tomar una hormiga.

¿Pero cuál es el más corto? Existe una forma ingeniosa de resolver el problema. ¡Aplanaremos el cubo!
Si el cubo está hecho de papel, puede cortarlo por los bordes y aplanar la hoja para obtener este patrón desplegado.

En un mundo tan plano, es fácil encontrar el camino más corto de A a B: simplemente dibuja una línea recta entre ellos.

Para ver cuál será la línea geodésica en el mundo del cubo, simplemente vuelva a colocar el cubo. Aquí está nuestro atajo.

“Alinear” el cubo funciona porque cada cara del cubo es plana, por lo que nada se distorsiona cuando desplegamos el cuerpo a lo largo de los bordes. (Este intento de "desplegar" la esfera no funcionará, ya que no podemos aplanar la esfera sin distorsionarla).
Ahora que tenemos una idea de cómo se ven los caminos en línea recta en un cubo, volvamos a la pregunta de si podemos seguir un camino recto y terminar de nuevo donde comenzamos. A diferencia de una esfera, en un cubo, no todos los caminos rectos nos llevan al principio.
Pero estas rutas de ida y vuelta son posibles. ¡Con un truco! Tenga en cuenta que la hormiga puede continuar por el camino que le indicamos anteriormente y regresar al lugar donde comenzó. En un cubo, un círculo completo crea un camino que se parece más a un diamante.

Siguiendo este camino (ida y vuelta), la hormiga debe pasar por otro vértice (punto B) antes de volver a su punto de partida. Este es el truco: cada camino recto que comienza y termina en el mismo vértice debe pasar por otro vértice del cubo.
Resulta que esto es cierto para cuatro de los cinco sólidos platónicos. En un cubo, tetraedro, octaedro e icosaedro, cualquier camino recto que comience y termine en el mismo vértice debe pasar por algún otro vértice a lo largo del camino. Los matemáticos demostraron esto hace cinco años, pero el dodecaedro no estaba en su lista. Volveremos a esto un poco más tarde.

Para entender por qué este hecho sobre geodésicas es cierto para cuatro de los cinco sólidos platónicos, usaremos el método de volteo y cambiaremos al mundo tetraédrico, donde este método se puede demostrar mejor.
Imagínese comenzar en la parte superior del tetraedro y caminar en línea recta a lo largo del borde. Coloque el tetraedro de modo que el camino comience desde el borde inferior.
Cuando nos encontramos con un borde, volteamos el tetraedro para que nuestro camino continúe a lo largo de la cara que resulta estar debajo:

Tales rotaciones hacen posible seguir nuestro camino de la misma manera que lo haríamos al desplegar un cubo:

La trayectoria de Las rotaciones de arriba representan este camino en la superficie del tetraedro:

Las cinco vueltas del tetraedro corresponden a las cinco caras adicionales cruzadas por nuestra ruta.
Ahora podemos imaginar cualquier camino en la superficie del tetraedro como un camino en este espacio "giratorio". Definamos nuestro punto de partida A y veamos dónde termina después de algunos giros.
Cuando nuestro camino sale del punto A, el tetraedro cae al lado opuesto. Esto eleva el punto A del suelo.

El vértice A se eleva temporalmente en nuestro mundo giratorio. Por lo general, no especificamos la ubicación del punto A cuando creamos nuestro espacio giratorio, pero aquí es donde podría aparecer si estuviéramos mirando hacia abajo.

A medida que nuestro camino continúa, el tetraedro vuelve a caer. Puede hacerlo en una de las dos direcciones posibles, pero en cualquier caso, A está nuevamente en la parte inferior.
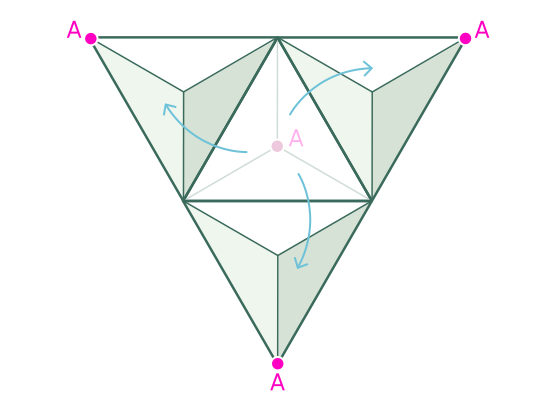
Cuando hacemos caer el tetraedro en todas las direcciones posibles, obtenemos un salto mortal que se ve así:

resulta una especie de celosía debido a que las caras triangulares equiláteras del tetraedro coinciden entre sí.

Esta cuadrícula triangular nos dice dos cosas interesantes sobre nuestro mundo giratorio. Primero, todos los puntos en los que los vértices del tetraedro pueden aterrizar son "puntos de celosía" (mostrados en el diagrama) o puntos con coordenadas enteras. Esto se debe a que una unidad en nuestro sistema de coordenadas es igual a la longitud de un borde del tetraedro.
En segundo lugar, observe dónde podría terminar A. Las
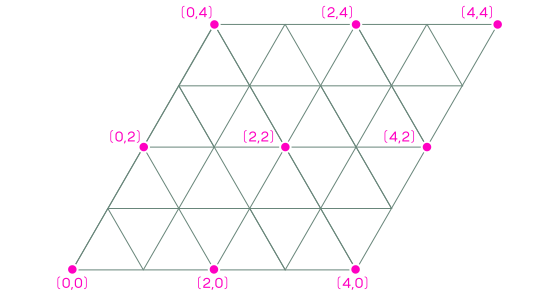
coordenadas de A son siempre pares. Siempre que A está abajo, vuelve allí después de dos giros, por lo que todos los posibles puntos de aterrizaje para A se colocan a intervalos de dos longitudes de costilla en cada dirección de giro.
Ahora veamos qué dice esto sobre las líneas geodésicas. Recuerde que una ruta en un tetraedro que comienza y termina en el punto A será un segmento de línea recta en el espacio rotatorio, comenzando en el punto A (0,0) y terminando en otro punto A. Y cuando los puntos de inicio y finalización de la ruta coinciden en un solo A, ¿qué habrá en el medio del camino?
Incluso en nuestro confuso sistema de coordenadas, la fórmula estándar para calcular el punto medio de un segmento de línea todavía funciona, por lo que podemos encontrar sus coordenadas en función de las coordenadas de los puntos finales.
Dado que ambas coordenadas del punto de inicio son 0 y ambas coordenadas del punto final son pares, las coordenadas del medio son números enteros. Es decir, el medio será uno de los puntos de la celosía y, como señalamos anteriormente, esto significa que corresponde al vértice del triángulo en el espacio giratorio.
Por ejemplo, la ruta de (0,0) a (4,2) tiene un punto medio (2,1), este es el punto de celosía marcado en nuestra cuadrícula.

Resulta que en la superficie del tetraedro, el camino desde A y hacia atrás debe pasar por otro vértice.
Dado que cada posible "aterrizaje" para A tiene coordenadas pares, el punto medio de cada trayectoria geodésica que comienza y termina en A corresponderá a un punto de cuadrícula. Esto prueba que toda línea geodésica de A a A en la superficie del tetraedro debe pasar por otro vértice.
Este simple razonamiento fue elaborado en 2015 por los matemáticos Diana Davis, Victor Dods, Cynthia Traub y Jed Young.
Utilizaron un método similar pero mucho más complejo para demostrar lo mismo para un cubo. Al año siguiente, Dmitry Fuks confirmóresultados para octaedro e icosaedro. Debido a esto, sabemos que para un tetraedro, cubo, octaedro e icosaedro no hay caminos rectos que vayan de un vértice hacia sí mismo que no pasarían por otro vértice.
Pero la cuestión de la existencia de tales caminos en la superficie del dodecaedro permaneció abierta hasta 2019, cuando los matemáticos Jayadev Atreya, David Avlikino y Patrick Hooper demostraron que de hecho era posible. De hecho, encontraron infinitos caminos rectos en la superficie del dodecaedro que comienzan y terminan en el mismo vértice sin pasar por otros.
Aquí está uno de ellos, representado en un escaneado de un dodecaedro, escondido a plena vista.

Durante miles de años, los sólidos platónicos se han estudiado juntos porque tienen mucho en común. Pero ahora sabemos algo nuevo sobre el dodecaedro, y esto lo distingue claramente de otros cuerpos.
Este misterioso descubrimiento muestra que no importa qué tan bien entendamos los objetos matemáticos, siempre hay algo que aprender. ¡Es importante recordar que el camino del problema a la solución no siempre será sencillo!
Tareas
1. Si la longitud de la arista de un cubo es 1, ¿cuál es el camino más corto para una hormiga desde un vértice al opuesto?
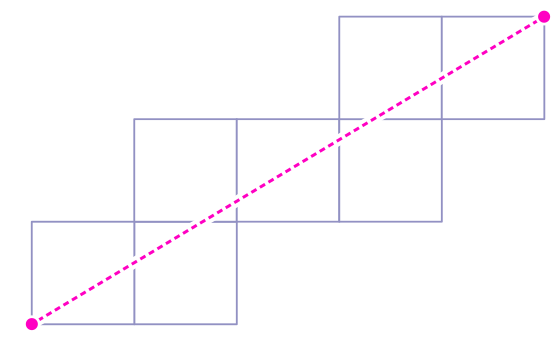
2. Explica por qué el siguiente diagrama no puede ser una ruta de rotación en un cubo.

3. Una de las dificultades de "rotar" un cubo es que el punto A no tiene una posición final única asociada con la posición final del cubo. Por ejemplo, incluso si el cubo está en el mismo lugar, girando a lo largo del camino rojo o azul, el punto A está en diferentes posiciones. Determine dónde estará A después de los giros a lo largo de la trayectoria roja y azul.

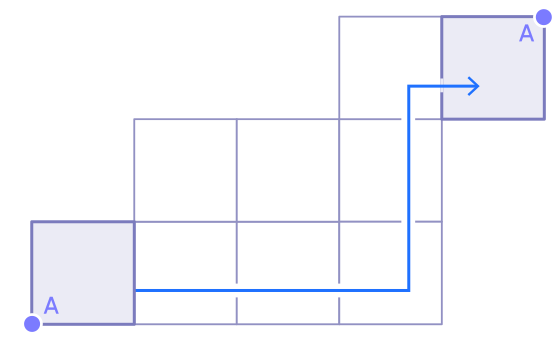
4. Esta es la trayectoria de las rotaciones del cubo.
Dibuja un camino en la superficie del cubo, comenzando en el punto A.

Respuestas
Haga clic para ver la respuesta 1
— 1 2.

, AB √5.

, AB √5.
Haga clic para ver la respuesta 2
, 1 . , , .

, «» , .

, «» , .
, 3
.

, .


, .
, 4

