
El modo de juego del simulador de vehículos consiste en controlar el movimiento de un objeto en el espacio con varios grados de libertad. Las acciones del jugador cambian el vector del estado instantáneo del sistema en la dirección deseada o no del todo deseada. Es poco probable que el juego sea interesante si el objeto está mal adaptado al control del jugador.
La adaptabilidad de un sistema técnico al control humano ( controlabilidad ) es una característica bastante compleja y multifacética. El modelo matemático del comportamiento de un objeto controlado es tratado por la teoría del control automático (TAU). Los modelos adoptados en TAU también pueden describir el comportamiento del jugador - sistemas “humano-operador” y “hombre-máquina”.
Cabe señalar que los modelos humanos creados son siempre relevantes para una gama limitada de condiciones. Por esta razón, la resolución de problemas prácticos en el campo de la controlabilidad a menudo va más allá del TAU.
La controlabilidad de una máquina se refiere a sus propiedades ergonómicas, que pierden su significado al aislarse del contexto de la actividad humana. Debajo del corte, se presenta un enfoque para configurar un modelo de simulador, basado en un estudio experimental del proceso del juego.
Para los simuladores que afirman simular con precisión los sistemas existentes, la similitud con el prototipo es importante, sin importar cuán pobre sea su manejo. La optimización de las mismas características es relevante para juegos que no tienen un modelo dado, por ejemplo, simuladores de objetos fantásticos.
Dejando de lado el problema de simular un objeto real con un conjunto dado de características, notamos que el simulador ciertamente no perderá la presencia de una fisicalidad determinada subjetivamente. En otras palabras, incluso un objeto que no existe en la naturaleza puede o no corresponder a las expectativas del jugador con respecto a su comportamiento (objeto). Debe tenerse en cuenta el factor de comportamiento natural del objeto.
Formulación del problema
Para el simulador, es necesario ajustar los coeficientes del modelo matemático del vehículo para asegurar su mejor manejo. La optimización debe realizarse sobre la base de datos experimentales. Es deseable obtener un modelo que se vea natural para el jugador.
Descripción del sistema
En nuestros experimentos usaremos un simulador con gráficos 3D .
La complejidad del modelo matemático de un vehículo real está limitada solo por el nivel aceptado de abstracción y la aspereza de los supuestos utilizados. La complejidad del modelo en el problema que se resuelve aquí está determinada por el nivel racional de la naturalidad del juego.
A continuación se aplicarán las siguientes simplificaciones:
1. Se considera que la dirección de movimiento del objeto coincide con su eje longitudinal.
2. El movimiento de rotación de un objeto se puede considerar como la suma de componentes independientes - movimientos de rotación relativos a los tres ejes del sistema de coordenadas (CCS) asociado con el objeto.
3. La aceleración angular en un canal de control separado (alrededor de un eje CCS separado) se determina mediante una combinación lineal de los valores actuales de la acción de control y la velocidad angular en este canal.
La aceptabilidad de la primera simplificación en el modelado de objetos reales está determinada por las propiedades del sistema y el problema que se resuelve. Por ejemplo, una propiedad bien conocida de los dardos es su capacidad para volar después de haber sido lanzados "con un punto hacia adelante". Este sencillo modelo es suficiente para sacar una conclusión útil: no arrojes el dardo sobre ti.

Pero si se necesita un modelo preciso para determinar las consecuencias del contacto de un dardo con un objetivo, entonces debe tenerse en cuenta que en vuelo su vector de velocidad forma un cierto ángulo con el eje longitudinal.
La constancia de la dirección del vector de velocidad en el sistema de coordenadas del objeto corresponde a la biomecánica de caminar: es más fácil para una persona caminar, manteniendo el estado de "mirar hacia adelante". El movimiento en direcciones inusuales, por el contrario, perjudica la visión del jugador y requiere un esfuerzo mental adicional de él.
El ítem 2 establece el mutuo aislamiento de los canales de control "adjuntos" a los ejes del SSC.
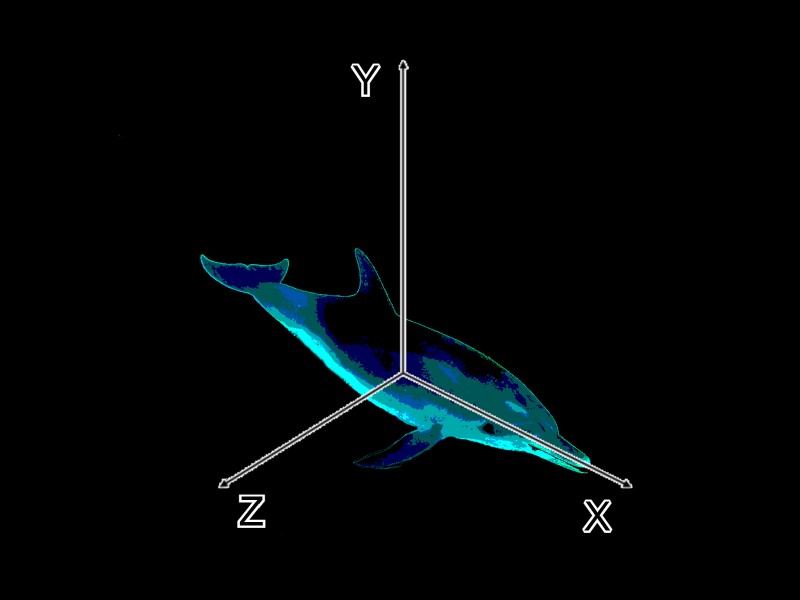
Ejes SSC: longitudinal ( X ) se dirige desde la cola hasta la nariz del objeto, vertical ( Y ) se dirige hacia arriba en el plano de simetría del objeto en su posición inicial, lateral ( Z ) se dirige perpendicular a los dos primeros hacia la derecha. En consecuencia, la rotación alrededor del eje X- canal lateral, alrededor del eje Y - canal de vía, alrededor del eje Z - canal longitudinal.
De acuerdo con la cláusula 2 de las simplificaciones adoptadas, no existen enlaces cruzados entre los canales de control del objeto. Los sistemas reales siempre corresponden a un modelo de este tipo con algún error causado, por ejemplo, por la presencia de momentos giroscópicos. La falta de enlaces cruzados es una ventaja desde el punto de vista del jugador.
El ítem 3 establece la presencia de solo dos pares en cada canal de control:
- controlar el torque proporcional a la señal del control del jugador;
- momento de amortiguación proporcional a la velocidad angular actual.
La ecuación diferencial de rotación alrededor del eje i es la siguiente:

Aquí omega es la velocidad angular de rotación, t es el tiempo, x es la señal de control y los coeficientes del lado derecho de la ecuación son las derivadas parciales de la aceleración angular de la señal de control y la velocidad angular.
El primer coeficiente se llamará coeficiente de eficiencia de control , el segundo, el coeficiente de amortiguación .
La aceleración angular se mide en [rad / s 2], la velocidad angular está en [rad / s]. La señal de control se suele medir en unidades de movimiento de las palancas o esfuerzos sobre ellas, menos frecuentemente en unidades de la posición de los elementos intermedios del sistema de control, pero para el control desde el teclado tomaremos este valor como adimensional. La dimensión del factor de amortiguación es [1 / s] y el factor de eficiencia de control es [rad / s 2 ], teniendo en cuenta la dimensión adoptada de la señal de control.
Información teórica requerida
, (1), . , . , :
(1) – x, – . :

(t) – , y(t) – , y – , k – , T – , .
(1) (2) :
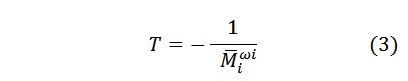
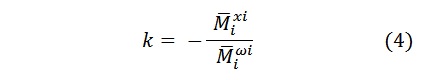
( ) , . () – . – .
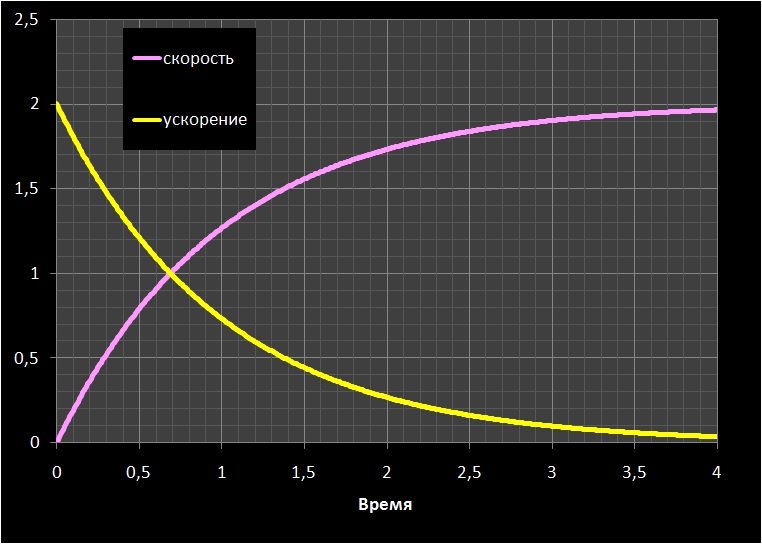
:

:
:
1. ( ), , .
2. , , .
3. , , , k.
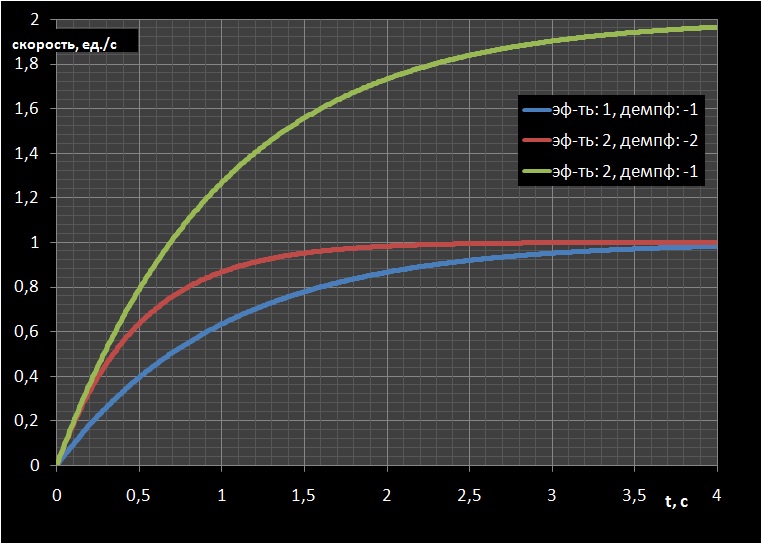
, . k T.
. .
. , : — , — , – . — - , .
, - , . .
, , . .

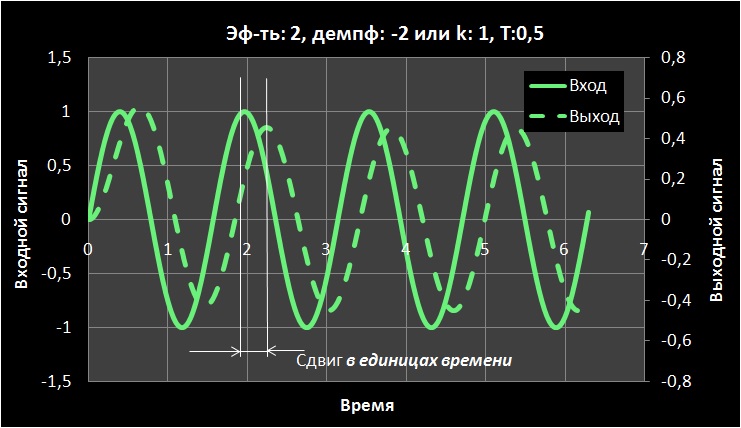
, . .
( ) k. .
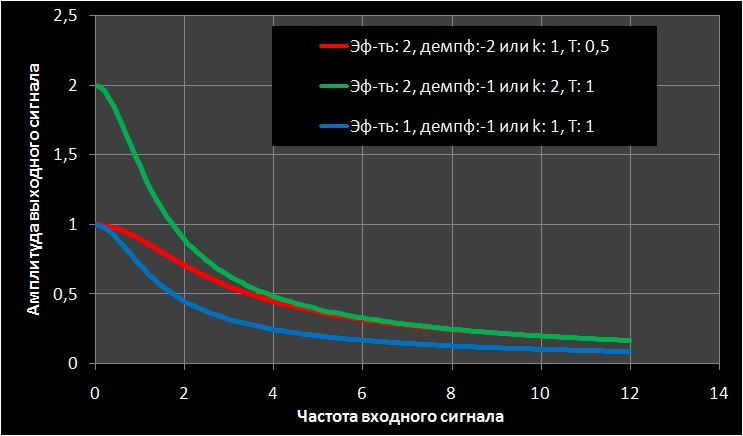
T ( ). T .
( T).
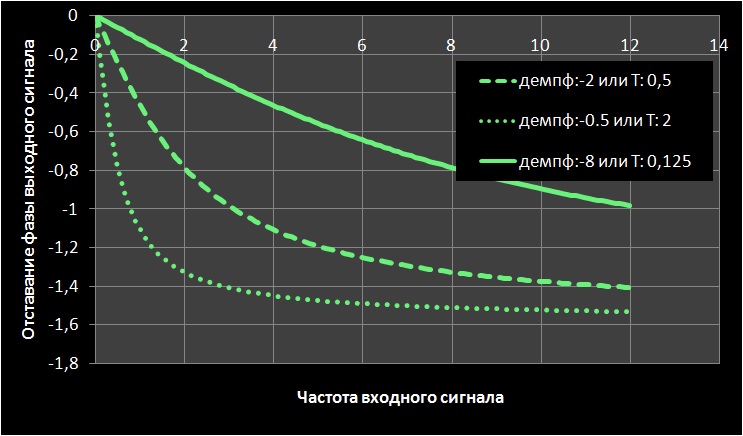
, /2. T.
: ( T) .
- ;
- ();
- ().
(1) – x, – . :

(t) – , y(t) – , y – , k – , T – , .
(1) (2) :
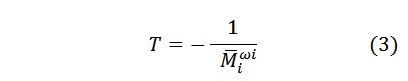
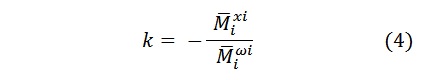
( ) , . () – . – .

:

:
- k ;
- T « », , t = 3T 0,95k.
:
1. ( ), , .
2. , , .
3. , , , k.

, . k T.
. .
. , : — , — , – . — - , .
, - , . .
, , . .


, . .
( ) k. .

T ( ). T .
( T).

, /2. T.
: ( T) .
Condiciones experimentales y criterios de calidad del modelo
Una mejor capacidad de control del objeto debería proporcionar una solución más eficiente al problema por parte del jugador. Pero las diferentes tareas requieren una capacidad de control diferente: el cumplimiento exacto de los parámetros de un modo de movimiento dado difiere significativamente de las maniobras intensivas.
Encontrar un modelo universal para cualquier tarea está inevitablemente asociado con un compromiso. Las condiciones experimentales determinan el cambio de equilibrio subjetivo a favor de determinadas tareas. Sin embargo, se deben elegir las condiciones específicas del juego.
Para el estudio, utilizaremos el problema de visitar un objeto controlado del número máximo de ubicaciones especificadas en un tiempo limitado. Una solución eficaz a este problema requiere maniobras intensivas.
El vehículo se controlará con restricciones en los ángulos de balanceo y cabeceo ( 60 grados en ambas direcciones para ambos ángulos): ir más allá de los límites provocará un accidente. Además, una colisión con una superficie horizontal ubicada sobre el objeto provoca un accidente. Esta parte de las condiciones es responsable del componente de mantener los parámetros en la tarea del jugador.
El valor del módulo de velocidad lineal del objeto se supone constante. Esto significa que no hay control del acelerador, así como el desnivel de la resistencia media, en el simulador.
Indicador de eficiencia del jugador: el número de ubicaciones visitadas antes del final del tiempo ( 60segundos) o antes del accidente. Cuantas más ubicaciones se visiten, mejor se considerará el modelo. Cada modelo (conjunto de valores de coeficientes) proporciona tres pases del juego teniendo en cuenta la puntuación media.
Al planificar experimentos, es importante minimizar la influencia del factor de aprendizaje. Para ello, se determinó el orden de los experimentos, en los que se lanza cada modelo en el primer, segundo y tercer tercios del estudio:
A, B, C ... N, O,
A, B, C ... N, O,
A, B, C ... N, O ...
Cada carrera experimental fue precedida por un juego de práctica con el modelo correspondiente.
Simulador
Puede experimentar con los coeficientes del modelo usted mismo aquí .
La gestión de probabilidades se encuentra en la esquina superior derecha de la pantalla. El parámetro "eficiencia" es el coeficiente de eficiencia de control, el parámetro "amortiguación" es el coeficiente de amortiguación tomado con el signo opuesto.
Control de juego:
- Espacio : comienzo del juego;
- W / S - rotación alrededor del eje SSC Z , nariz hacia abajo / nariz hacia arriba;
- A / D - rotación alrededor del eje Y del SSK, girar a la izquierda / girar a la derecha;
- 4/6 en el teclado numérico: rotación alrededor del eje X del SSK, rodar a la izquierda / rodar a la derecha.
El jugador del parabrisas indicador ve el horizonte artificial y el valor actual del rumbo ( «rumbo» ) y la profundidad ( «profundidad» ), es decir, la distancia a la superficie peligrosa. También muestra el resto del tiempo de juego y el resultado actual ( "puntuación" ): el número de ubicaciones visitadas.
El código del simulador está escrito en JavaScript utilizando la biblioteca Three.js . Los valores de los parámetros del movimiento del objeto se actualizan en el ciclo del juego integrando numéricamente la ecuación (1) utilizando el método de Euler. En cada iteración, se llama al método update () del objeto vehículo , realizando cálculos para cada canal de control:
vehicle.update = function () {
// :
game.elapsed = (new Date() - game.time) / 1000;
game.time = new Date();
// ...
// :
vehicle.omegaX += (vehicle.epsilonX - vehicle.omegaX * vehicle.damping) * game.elapsed;
vehicle.omegaY += (vehicle.epsilonY - vehicle.omegaY * vehicle.damping) * game.elapsed;
vehicle.omegaZ += (vehicle.epsilonZ - vehicle.omegaZ * vehicle.damping) * game.elapsed;
// ...
}
Los campos epsilonX , epsilonY y epsilonZ del objeto del vehículo contienen los componentes de aceleración angular en ausencia de amortiguación. El valor de cada uno de estos campos se obtiene “multiplicando” la señal de entrada por el factor de eficiencia de control:
function init() {
// ...
// :
document.addEventListener('keydown', function (event) {
if (game.state == "READINESS")
if (event.code == "Space") {
// ...
}
if (game.state == "RUN")
switch (event.code) {
case "KeyW":
vehicle.epsilonZ = vehicle.efficiency;
break;
case "KeyS":
vehicle.epsilonZ = -vehicle.efficiency;
break;
case "KeyA":
vehicle.epsilonY = -vehicle.efficiency;
break;
case "KeyD":
vehicle.epsilonY = vehicle.efficiency;
break;
case "Numpad4":
vehicle.epsilonX = vehicle.efficiency;
break;
case "Numpad6":
vehicle.epsilonX = -vehicle.efficiency;
break;
}
});
document.addEventListener('keyup', function (event) {
switch (event.code) {
case "KeyW":
vehicle.epsilonZ = 0;
break;
case "KeyS":
vehicle.epsilonZ = 0;
break;
case "KeyA":
vehicle.epsilonY = 0;
break;
case "KeyD":
vehicle.epsilonY = 0;
break;
case "Numpad4":
vehicle.epsilonX = 0;
break;
case "Numpad6":
vehicle.epsilonX = 0;
break;
}
});
// ...
}
Resultados del experimento
El indicador de calidad del modelo se considerará en función de dos variables. En consecuencia, los resultados del estudio representan gráficamente una superficie 3D , cada punto de la cual define su propio modelo del objeto controlado.

Consideremos las características clave de algunos modelos. En la tabla, los modelos discutidos se indican en letras latinas.
Con el valor mínimo del coeficiente de eficiencia de control ( 0.5 rad / s 2 ), existe un modelo con el mejor valor del coeficiente de amortiguamiento (punto A ). El modelo A se caracteriza por una capacidad débil del objeto para maniobras dinámicas.
El cambio del modelo A hacia una mayor amortiguación conduce a la creación de modelos con valores de velocidad angular máxima extremadamente bajos. El objeto finalmente pierde su capacidad de maniobra.
Cambiar el modelo A en la dirección de disminuir la amortiguación mejora parcialmente la maniobrabilidad del objeto, pero la calidad general del sistema disminuye debido al deterioro de sus propiedades dinámicas: surge un problema de balanceo, el control requiere acciones de compensación constantes por parte del jugador.
En ausencia de amortiguación, existe un modelo con una eficiencia de control óptima ( B ). Su eficiencia de gestión es superior a la del modelo A, que proporciona una buena maniobrabilidad. En este caso, el problema de acumulación se agrava en comparación con el modelo A , completamente desprovisto de amortiguación.
El cambio del modelo B hacia un control más eficiente lleva el problema del swing a un nivel en el que el jugador presta toda su atención a combatirlo. Además, se vuelve imposible maniobrar sin ir más allá de las restricciones.
El modelo C combina las ventajas de los modelos A y Bed y . El objeto se gestiona con la suficiente eficacia, pero sin balancearse. El valor del indicador de rendimiento del juego para el modelo Csignificativamente más alto que los modelos anteriores. Sin embargo, este modelo no es el más eficaz.
El juego de rendimiento de las isolíneas de forma alrededor del punto C muestra que la mejora en el resultado corresponde al modelo D de dirección de movimiento .
Este movimiento corresponde a una disminución en el valor de T mientras se mantiene k a un nivel constante (alrededor de 0,6 rad / s). Los modelos entre C y D superan a Csobre la efectividad del juego. Al jugar con estos modelos, el objeto de control sigue más de cerca las pulsaciones de teclas.
Al pasar del modelo C al modelo D , se produce otro cambio: el deterioro del comportamiento natural del objeto. La constante de tiempo se acerca al nivel en el que la duración del transitorio y el desplazamiento de fase de la señal de salida ya no son perceptibles para el usuario.
Cambiar el modelo D hacia una mayor disminución en el valor de T mientras se mantiene el valor de k ya no proporciona mejoras significativas, porque el cambio de fase de la señal de salida y la duración del proceso transitorio en el modelo D ya es lo suficientemente pequeño para que el jugador lo perciba.
Los modelos obtenidos mediante una mayor "mejora" de D , desde el punto de vista del jugador, no difieren de la implementación del enlace amplificador: no hay aceleración angular del objeto en el juego, la velocidad angular adquiere instantáneamente un valor constante cuando se presiona la tecla.
El análisis realizado nos permite sacar las siguientes conclusiones :
1. Los valores óptimos de los parámetros del modelo corresponden a su degeneración en un enlace amplificador (el valor de k es alrededor de 0.6 rad / s, T = 0 s) y la pérdida del comportamiento natural del objeto.
2. El modelo que proporciona una buena controlabilidad con el comportamiento natural del objeto corresponde al punto C del gráfico (coeficiente de eficiencia de control: de 2 a 3 rad / s 2 ; coeficiente de amortiguación: de -4,5 a -3,5 1 / s).
3. Cambiar el modelo C en la dirección de disminuir el valor de T en k = const permite obtener un objeto con una mejor controlabilidad debido al deterioro de la naturalidad de su comportamiento.
Factores no contabilizados
Junto con las simplificaciones de la física del objeto controlado, la calidad de los resultados de la investigación se ve influenciada por otras simplificaciones de las condiciones de investigación:
1. El modelo de controlabilidad fue descrito por dos valores de los parámetros, el objeto se comportó igual en todos los canales de control. Para obtener una imagen precisa, deben variarse los valores de seis parámetros, ya que no hay razón para considerar las propiedades del reproductor iguales para todos los canales.
2. Los resultados obtenidos son relevantes para la configuración del campo de visión de la cámara utilizada en el juego. Cambiar este parámetro tendrá un efecto notable en la interacción del jugador con el objeto.
El defecto más grave del estudio es la falta de estadísticas. Cualquier investigación ergonómica debe centrarse en las propiedades del público objetivo en su conjunto. Se pueden obtener resultados más completos con la participación de un grupo de jugadores.