Durante mucho tiempo, los matemáticos han intentado resolver el problema de una cabra pastando atada a una cerca. Pero hasta ahora, solo podían ofrecer soluciones aproximadas.

Aquí tienes una tarea sencilla . Imagínese un seto en forma de círculo, con un área de pasto conocida con precisión encerrada dentro. Pones una cabra adentro y la atas con una cuerda a la cerca. ¿Cuánto tiempo necesita la cuerda para que la cabra tenga acceso exactamente a la mitad de esta área?
Parece una tarea de geometría de la escuela secundaria; sin embargo, matemáticos profesionales y aficionados lo han pensado en diferentes formulaciones durante más de 270 años. Algunas variantes de este problema se han resuelto con éxito, pero el acertijo de una cabra dentro de un círculo no nos ha dado más que respuestas vagas e incompletas.
Hasta el día de hoy, "nadie sabía la respuesta exacta a la pregunta básica", dijo Mark Meyerson., matemático de la Academia de la Marina de los Estados Unidos. "La solución siempre ha sido dura".
Sin embargo, en 2020, el matemático alemán Ingo Ullisch finalmente avanzó . Encontró, como se cree, la primera solución exacta a este problema, aunque parece bastante engorroso e incomprensible.
"Esta es la primera expresión precisa de longitud de cuerda que conozco", dijo Michael Harrison , matemático de la Universidad Carnegie Mellon. "Este es definitivamente un gran avance".
Ullisch reconoce que su decisión no tachará los libros de texto ni impulsará revoluciones matemáticas. Esta tarea está aislada. "No está relacionado con otros problemas y no está incluido en ninguna teoría matemática". Pero siempre existe la posibilidad de que tal acertijo dé lugar a nuevas ideas matemáticas o ayude a los investigadores a encontrar otros enfoques para otros problemas.
En y alrededor del corral
El primer problema de este tipo se publicó en 1748 en la revista femenina periódica londinense The Ladies Diary: Or, The Woman's Almanack [Diario de la dama o Almanaque de la mujer]. La revista prometía "nuevas mejoras en las artes y las ciencias y muchas pequeñas cosas divertidas".
El escenario original presenta un caballo pastando con una correa en un parque. En la faena, el caballo estaba atado fuera de la cerca. Si la longitud de la cuerda coincide con la circunferencia de la cerca, ¿en qué área puede pastar el caballo? Posteriormente, esta tarea se denominó “afuera”, porque el pasto que había en él no estaba dentro del círculo, sino afuera.

La respuesta al acertijo apareció en el número de 1749. La respuesta fue compilada por un "Sr. Heath", basado, entre otras cosas, en el libro de referencia de "tablas de investigación y logaritmos". Dio la respuesta: 76,257.86 yardas cuadradas con 160 yardas de cuerda. Y esta fue una respuesta aproximada, no un cálculo exacto. Permítanos explicarlo con un ejemplo: puede escribir una respuesta numérica aproximada a la ecuación x 2 - 2 = 0, x = 1.4142, pero esto no será tan exacto o satisfactorio como x = √2.
El problema apareció de nuevo en 1894 en el primer número del American Mathematical Monthly, revisado para el caso en que el animal pasta dentro de la cerca. Este tipo de tarea se denomina "interna" y, en promedio, son más difíciles que las externas, explicó Ullisch. En el problema externo, puede comenzar desde el radio del círculo y la longitud de la cuerda, y luego calcular el área. Se puede resolver mediante integrales.
“Resolverlo en la dirección opuesta, comenzando con un área determinada y preguntando qué entradas conducen a ella, es mucho más difícil”, dijo Ullisch.
En las décadas siguientes, el mensual publicó diferentes versiones del problema interno, en su mayoría con caballos (y en al menos un caso, un mulo) en lugar de cabras. Había vallas redondas, cuadradas y elípticas. Pero en la década de 1960, por misteriosas razones, las cabras comenzaron a suplantar gradualmente a los caballos en la literatura. A pesar de que, según el matemático Marshall Fraser, las cabras son "demasiado independientes para vivir con una correa".
Cabras en las dimensiones superiores
En 1984, Fraser se puso creativo al llevar el problema de un tema pastoral plano a un paisaje más complejo. Se calcula cuánto tiempo se necesitaría una cuerda de una cabra a pastar en exactamente la mitad del volumen de una esfera de dimensión n cuando n tiende a infinito. Meyerson encontró un error lógico en su razonamiento y más tarde ese mismo año lo corrigió , pero llegó a la misma conclusión. Cuando n se acerca al infinito, la relación entre la longitud de la cuerda y el radio de la esfera tiende a √2.
Meyerson señaló que esta forma aparentemente más compleja de describir el problema, en un espacio multidimensional en lugar de un campo con césped, en realidad hizo que fuera más fácil encontrar una solución. "En un número infinito de dimensiones, tenemos una respuesta exacta, y en dos dimensiones, no existe una solución tan clara".
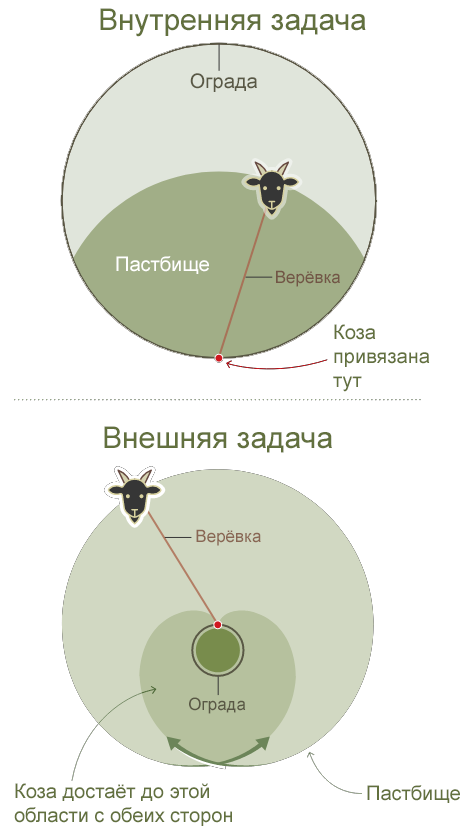
Hay dos tipos de problemas para una cabra en pastoreo. Ambos están asociados con una cabra atada a una cerca redonda. La versión interna pregunta por la longitud de la cuerda que dará acceso exactamente a la mitad del área cerrada. Afuera pregunta a qué área tiene acceso la cabra dada la longitud de la cuerda y el radio de la cerca (en la imagen, la longitud de la cuerda es igual a la circunferencia de la cerca).
En 1998, Michael Hoffman, otro matemático de la Academia Naval de Estados Unidos, amplió el problema en una dirección diferente cuando se topó con un ejemplo de un problema externo en un grupo de noticias. En esa versión, era necesario estimar el área disponible para un toro atado al exterior de un silo circular. El problema interesó a Hoffman, y decidió generalizarlo no solo a un círculo, sino a cualquier curva convexa suave, incluidas las elipses e incluso las curvas no cerradas.
"Cuando se enfrenta a una declaración de problema para un caso simple, un matemático intentará averiguar cómo se puede generalizar", dijo Hoffman.
Hoffman consideró el caso en el que un arnés de longitud L es menor o igual a la mitad de la longitud de la curva. Primero, trazó una línea tangente donde se ata la cuerda. Un toro puede pastar en semicírculo con un área de πL 2/ 2 delimitado por una tangente. Luego, Hoffman calculó el área exacta entre la tangente y la curva a través de una integral.
Más tarde, Graham Jameson , matemático de la Universidad de Lancaster, y su hijo Nicholas propusieron una solución detallada a un problema interno en tres dimensiones. Eligieron esta ocasión porque era menos popular. Debido a que las cabras no pueden moverse en tres dimensiones con tanta facilidad, Jameson denominó a esta tarea el "problema de las aves" en un artículo de 2017. Suena así: si atas un pájaro a una jaula esférica, ¿cuánto tiempo debe tener la cuerda para limitar su movimiento exactamente a la mitad de su volumen?
“El problema en tres dimensiones es más fácil de resolver que en dos”, dijo Jameson Sr. Como resultado, a la pareja se le ocurrió la solución exacta. Sin embargo, dado que la forma matemática de la respuesta era, en palabras de Jameson, "precisa pero terrible" y podría asustar a los investigadores sin experiencia, también se les ocurrió un método de cálculo aproximado que cuantifica la longitud de la cuerda que "los amantes de las aves disfrutarán".
Conseguir la cabra
Sin embargo, la solución exacta del problema bidimensional en la formulación de 1894 eludió a los matemáticos, hasta la aparición del trabajo de Ullisch en 2020. Ullish escuchó por primera vez sobre esta tarea de un pariente en 2001, cuando aún era un niño. Comenzó a trabajar en él en 2017, recibiendo su doctorado de la Universidad Wilhelm de Westfalia en Münster. Decidió probar un nuevo enfoque.
En ese momento, era bien sabido que el problema de la cabra podría reducirse a una sola ecuación trascendental , que por definición incluye términos trigonométricos como seno y coseno. Esto podría crear un problema, ya que muchas ecuaciones trascendentales no se pueden resolver. Por ejemplo, la ecuación x = cos (x) no tiene soluciones exactas.

Ingo Ullish
Sin embargo, Ullish formuló el problema de tal manera que se diera a sí mismo una ecuación trascendental más maleable: sin (β) - β cos (β) - π / 2 = 0. Y aunque también puede parecer inaccesible, se dio cuenta de que se puede abordar utilizando un complejo análisis : una rama de las matemáticas que aplica herramientas analíticas a ecuaciones con números complejos. El análisis exhaustivo ha existido durante siglos, pero Ullish, hasta donde él sabe, fue el primero en adoptar este enfoque para las cabras hambrientas.
Con esta estrategia, pudo convertir su ecuación trascendental en una expresión equivalente para la longitud de la cuerda que permitiría a la cabra pastar en la mitad del área confinada. Es decir, finalmente respondió a la pregunta utilizando fórmulas matemáticas precisas.

La solución al problema se da en forma del coseno de la relación de dos integrales curvilíneas (fórmula de Wikipedia).
Desafortunadamente, hay una trampa. La solución de Ullisch no es una expresión simple como la raíz cuadrada de 2. Es algo tan complejo como la razón de dos integrales curvilíneas mezcladas con diferentes funciones trigonométricas. Desde un punto de vista práctico, no le dirá exactamente cuánto tiempo debe ser la correa de una cabra. Para obtener una respuesta que sea aplicable a la agricultura, aún necesita hacer algunos cálculos aproximados.
Pero Ullish todavía cree que la solución exacta es valiosa, incluso si no es tan hermosa y simple. “Si solo usamos valores numéricos o aproximaciones, no entenderemos la esencia de la naturaleza de la solución”, dijo. "La fórmula nos da una idea de cómo se deriva la solución".
No renuncies a la cabra
Ullisch ha dejado a un lado la cabra de pastoreo por ahora, ya que no está seguro de adónde ir a continuación. Pero otros matemáticos ya están desarrollando sus propias ideas. Harrison, por ejemplo, está preparando un artículo para su publicación en Mathematics Magazine, donde explora las propiedades de una esfera para abordar una generalización tridimensional del problema de las cabras.
"En matemáticas, a menudo es útil encontrar nuevas formas de obtener una respuesta, incluso para problemas que ya se han resuelto", señaló Meyerson, "ya que puede ser posible generalizar todo esto para usarlo en otros problemas".
Por eso los matemáticos han gastado tanta tinta en animales imaginarios. “Mi instinto nos dice que trabajar en el problema de las cabras en pastoreo no nos dará ningún avance”, dijo Harrison, “pero no puedes estar seguro. Las nuevas matemáticas pueden venir de cualquier parte ".
Hoffman es más optimista. La ecuación trascendental de Ullisch está relacionada con las ecuaciones trascendentales que Hoffman estudió en un artículo de 2017. Él, a su vez, se interesó por ellos gracias al trabajo de 1953, que exhibió los métodos convencionales bajo una nueva luz. Este enfoque le recuerda cómo Ullisch aplicó métodos bien conocidos en el análisis complejo a ecuaciones trascendentales en nuevas condiciones, en este caso, en el problema de los progos.
"Las personas que logran avances fundamentales en matemáticas no son responsables de todo el progreso", dijo Hoffman. "A veces se debe al hecho de que alguien estudia los enfoques clásicos y encuentra en ellos nuevos métodos para resolver el rompecabezas, que al final pueden conducir a nuevos resultados".