
La reacción al trabajo "Fórmula para resolver una ecuación de 4 ° grado" publicado el 12 de enero de 2021 en Habré , indicó que el artículo no estaba bien estructurado metódicamente. Las fórmulas no podían defenderse por sí mismas.
Intentaré arreglar la situación.
Entonces, la ecuación es de 4 grados.
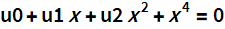
Primero sobre el método Ferrari.
El método Ferrari es notable porque captura la esencia de la ecuación de cuarto grado. La selección de cuadrados perfectos conduce a la aparición de un resolutivo cúbico. Como resultado, la ecuación se puede representar como un producto de dos polinomios cuadrados.
Para una ecuación de 5 y 6 grados, la técnica asociada con la selección de cuadrados o cubos completos muy rápidamente termina en nada. Me parece que es precisamente esta circunstancia la que realmente dio lugar a la tesis sobre la imposibilidad de resolver ecuaciones en radicales por encima del 4º grado.
Ecuación de solvente:
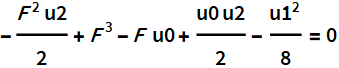
El producto de dos polinomios cuadrados obtenidos por el método de Ferrari.

Coeficientes de la expresión del lado derecho de la identidad.

A continuación, sustituimos la expresión por F ^ 3 del resolutivo y obtenemos el polinomio original de grado 4.
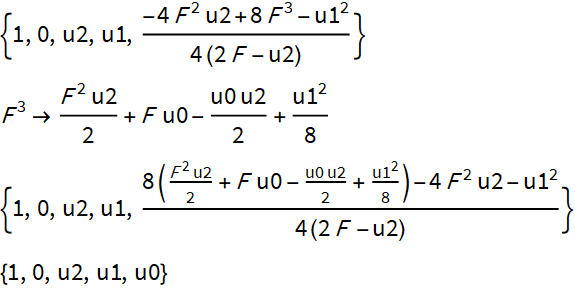
Lo único que hay que tener en cuenta es que el resolutivo aparece solo al calcular la intersección.
Las raíces de la misma ecuación deben ser idénticas sin importar el método que se obtenga.
En la práctica, dependiendo del método utilizado, se obtienen raíces, sobre las cuales en su representación simbólica es difícil decir si son idénticas o no. ¿Por qué no tener otro método de solución, que en algunos casos proporciona representaciones simbólicas de raíces más simples? Esta posibilidad es importante a la hora de elegir los valores de los parámetros de las raíces y conjugar las raíces de varias ecuaciones.
Diferencias entre el método ftvmetrics y el método Ferrari:
- otras ecuaciones auxiliares (solventes);
- las ecuaciones auxiliares "funcionan" no en el término libre, sino en los coeficientes del primer y segundo grados;
- Es posible calcular dos raíces de la ecuación de cuarto grado a partir de una ecuación cúbica, presentada en forma canónica.
Primera solución.
Se dio en el artículo mencionado al principio.
Ecuación auxiliar

El producto de polinomios cuadráticos, que es idéntico a la ecuación de cuarto grado después del reemplazo repetido R ^ 3
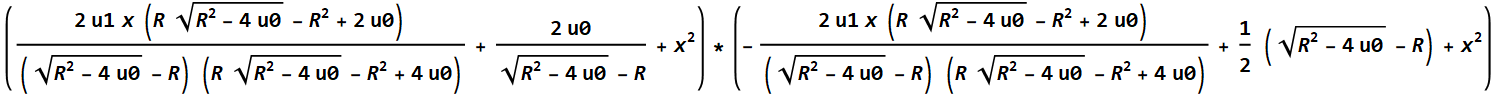
En lugar de resolver cada uno de los polinomios cuadráticos indicados anteriormente, en el método ftvmetrics, puede encontrar las raíces de la ecuación cúbica.

Dos de ellas serán las raíces de la ecuación de cuarto grado.
En este caso, es posible expresar las raíces en términos de funciones exponenciales o trigonométricas.
Puedes asegurarte de que la ecuación alternativa es correcta calculando los subresultantes y comprobando los dos primeros valores.
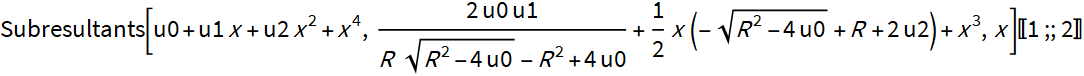
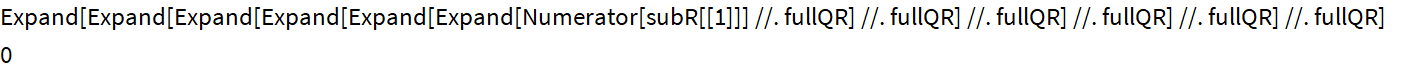

Las expresiones resultantes de los subresultantes son "brutales", pero cuando sabes lo que estás buscando, no todo es tan triste.
Segunda solución.
La ecuación auxiliar
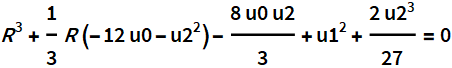
tiene forma canónica.
El producto de polinomios cuadráticos, idéntico a la ecuación de grado 4 después del reemplazo repetido R ^ 3. La

corrección de la ecuación alternativa también se verifica mediante subresultantes
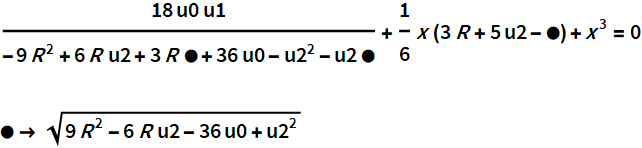
En la segunda solución, las ecuaciones auxiliares y alternativas tienen una representación canónica.
Es curioso conseguir algo nuevo después de 400 años.
Envíe tareas comerciales interesantes a Direct Instagram .