
Construye un octágono convexo con cuatro ángulos rectos.
Probablemente, el hecho de que dé tales asignaciones dice mucho sobre mí como maestra. Veo a los estudiantes tratar de alinear los ángulos rectos de manera consistente. Cuando fallan, intentan intercalar ángulos rectos. Fallando nuevamente, los insertan al azar en el polígono. El traqueteo de sus cerebros durante el esfuerzo mental es música para los oídos del maestro.
Entonces sospechan y empiezan a hacer preguntas. “Mencionaste ángulos rectos. ¿Quizás realmente quisiste decir tres esquinas? ”,“ ¿Definitivamente te refieres a un polígono convexo? ”,“ Cuatro ángulos rectos, de hecho, forman un rectángulo. ¿Cómo podemos tener cuatro lados más en el octágono? " Escucho con atención, asiento, confirmando sus conjeturas.
Finalmente, alguien hace la pregunta que nadie se atrevió a hacer, la pregunta que estaba esperando: "Oye, ¿esto es posible?"
Esta pregunta tiene el poder de cambiar tu forma de pensar en matemáticas. Aquellos que pensaban de manera limitada sobre condiciones específicas ahora deben pensar de manera más amplia sobre cómo encajan estas condiciones. Quienes trabajan dentro del sistema deben dar un paso atrás y estudiar el sistema en sí. A lo largo de la historia de las matemáticas, esta pregunta se ha formulado muchas veces, ha desconcertado a quienes resolvieron el problema de cuadrar un círculo para moverse por la ciudad de Königsberg . Y esta pregunta nos permite formular qué son las matemáticas y cómo las entendemos.
Por ejemplo, encontrar un octágono con ciertas propiedades es muy diferente a la tarea de demostrar que tal octágono no puede existir. Al experimentar con diferentes octágonos, podríamos encontrar uno con cuatro ángulos rectos.
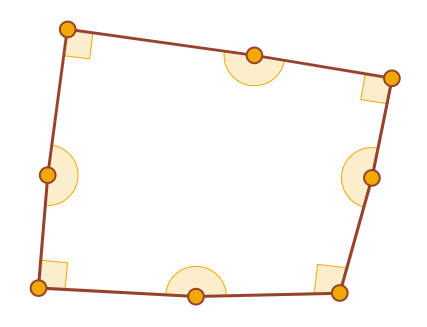
Este no es un ejemplo. De hecho, este octágono no tiene cuatro ángulos rectos.
Pero la suerte no juega ningún papel a la hora de demostrar que tal octágono no puede existir. Requiere un conocimiento profundo, no solo de polígonos, sino de las matemáticas mismas. Para dar cuenta de la imposibilidad, necesitamos entender que simplemente asumir la existencia de un objeto no prueba su existencia. Las definiciones, propiedades y teoremas matemáticos viven bajo la presión de su interconexión. Al tratar de representar un octágono con cuatro ángulos rectos, estamos dentro de estas reglas interrelacionadas.
Pero para darnos cuenta de que un octágono es imposible, debemos dar un paso atrás y mirar el panorama general. ¿Qué principios matemáticos y geométricos puede violar un octágono con cuatro ángulos rectos? Un buen lugar para comenzar aquí es con la suma de los ángulos de un teorema de polígono.
La suma de los ángulos interiores de un polígono de n lados está determinada por la fórmula:
S = ( n - 2) × 180º
Esto sucedió porque cada polígono de n lados se puede cortar en ( n - 2) triángulos, la suma de los ángulos interiores de cada uno de los cuales es 180º.
En el caso de un octágono, esto significa que la suma de sus ángulos interiores es (8 - 2) × 180º = 6 × 180º = 1080º. Entonces, si cuatro de sus esquinas son rectas, es decir, cada una es de 90º, entonces esto es 4 × 90º = 360º de los ángulos totales. Esto significa que quedan 1080º - 360º = 720º para las cuatro esquinas restantes del octágono.
Esto significa que el promedio de las cuatro esquinas restantes debe ser:
Pero los ángulos interiores de un polígono convexo deben ser menores de 180º, lo cual es imposible. No puede existir un octágono convexo con cuatro ángulos rectos.
Probar la imposibilidad de esta manera requiere dar un paso atrás y ver cómo varias reglas matemáticas, como la fórmula para la suma de los ángulos de un polígono y la definición de un polígono convexo, existen en presión mutua. Y dado que las pruebas de imposibilidad se basan en un razonamiento más amplio sobre un conjunto de reglas, a menudo hay varias formas de construir dicha prueba.
Regresemos a nuestra observación anterior de que cuatro ángulos rectos forman un rectángulo.
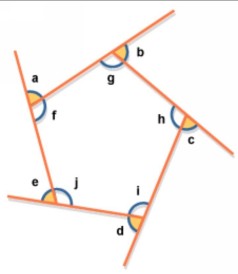
Esquinas exteriores del polígono.
Si el octágono tuviera cuatro ángulos rectos, entonces rodeando solo estas esquinas, haríamos un círculo completo, como si hubiéramos caminado completamente alrededor del rectángulo. Este pensamiento nos lleva a una regla que proporciona una prueba más de la imposibilidad. Se sabe que la suma de los ángulos exteriores de un polígono convexo es siempre 360º. Dado que la esquina exterior de un ángulo recto también es un ángulo recto, nuestros cuatro ángulos rectos forman los 360º completos de la suma de los ángulos exteriores del octágono. Es decir, al resto de las cuatro esquinas no les queda nada, y nuevamente establecimos que tal octágono es imposible.
Probar que algo es imposible es un poderoso evento matemático. Cambia nuestro punto de vista, pasamos de obedecer reglas a controlar reglas. Y para controlar las reglas, primero debemos comprenderlas. No solo debemos saber cómo aplicarlos, sino también situaciones en las que no son aplicables. Y también encuentre situaciones en las que las reglas puedan entrar en conflicto entre sí. En el proceso de estudiar el octágono, identificamos la relación de polígonos, convexidad, ángulos rectos y sumas de ángulos. Y esto enfatiza que S = ( n - 2) × 180º no es solo una fórmula: es una de las condiciones en el mundo de condiciones conflictivas.
Las pruebas de imposibilidad pueden ayudarnos a comprender mejor todas las áreas de las matemáticas. En la escuela, las lecciones de teoría de la probabilidad a menudo comienzan lanzando muchas monedas imaginarias. Invito a los estudiantes a crear una moneda fraudulenta que tiende a salir cara o cruz, que tiene la siguiente propiedad: cuando se lanza una moneda dos veces, es más probable que los resultados de las dos vueltas sean diferentes a lo mismo. En otras palabras, es más probable que arroje cara y cruz que cara y cruz o cruz y cruz.
Después de la experimentación y los fracasos mentales, los estudiantes plantean una hipótesis interesante: nunca es más probable obtener resultados diferentes que iguales. El álgebra revela esto y señala la simetría subyacente.
Digamos que la moneda se desplaza hacia las caras. Llamaremos a la probabilidad de sacar caradónde ... El hecho de que, garantiza que las caras son más probables que las cruces con probabilidad ya que la suma de las dos probabilidades debe ser 1.
Si lanzamos una moneda dos veces, la probabilidad de obtener dos caras o dos cruces es
Aquí sumamos la probabilidad de obtener dos caras (lado izquierdo) con la probabilidad de obtener dos cruces (lado derecho). Usando álgebra, podemos simplificar la probabilidad de obtener el mismo resultado en ambas tiradas:
...
En la medida en, Lo sabemos $, lo que significa que es más probable que los lanzamientos tengan los mismos resultados. De hecho, vemos que incluso si (la moneda no es fraudulenta), la probabilidad de los mismos resultados es , debido a que la probabilidad de diferentes resultados de lanzamientos también es ... El mismo resultado nunca será menos probable que otros diferentes.
Como en el caso del problema del polígono, vemos presiones matemáticas en competencia: cambiar la probabilidad de obtener un lado de la moneda cambia la probabilidad de obtener el otro, y esta interconexión controla el espacio de posibilidades para los resultados de dos lanzamientos. Expusimos esta presión tratando de lograr lo imposible.
Cualquier área de las matemáticas puede estar sujeta a tales presiones. Intente encontrar seis números enteros consecutivos que sumen 342 y su persistencia lo llevará a una comprensión más profunda de la paridad. (El hecho de que los enteros consecutivos se vuelvan pares e impares alternativamente afecta cómo pueden ser sus sumas). Encontrar un polinomio cúbico con coeficientes enteros que tenga tres raíces no reales le enseña la importancia de conjugar números complejos: pares de números complejos, producto y cuya suma es siempre real. Y si intenta inscribir un rombo no rectangular en un círculo, descubrirá una propiedad importante de los cuadriláteros cíclicos: las esquinas opuestas de un cuadrilátero, cuyos vértices se encuentran en el círculo, deben sumar 180 grados.
Afrontar lo imposible nos permite explorar los límites de nuestros mundos matemáticos. Lo imposible en sí mismo es una especie de generalización, por lo que sería natural continuar con la generalización: un octágono no puede tener cuatro ángulos rectos, pero ¿qué pasa con un decágono? ¿Qué tal un polígono convexo con n > 4 lados? Preguntas como estas se topan con los límites de nuestros mundos matemáticos y profundizan su comprensión.
Si empujamos los límites más allá, entonces lo imposible puede incluso inspirar la creación de nuevos mundos matemáticos. Para probar la imposibilidad de cuadrar el círculo(este problema tiene al menos dos mil años), se necesita una teoría moderna de los números trascendentales, que no pueden ser las raíces de polinomios enteros. Para resolver el problema de los siete puentes de Königsberg, Euler convirtió islas y puentes en vértices y aristas, dando origen a vastas áreas de teoría de grafos y teoría de redes, así como a muchas de sus aplicaciones. Sacar la raíz cuadrada de -1 condujo a un sistema aritmético completamente nuevo . Y el lógico Kurt Gödel cambió las matemáticas para siempre, demostrando que es imposible demostrar que todo lo que es cierto es cierto.
Entonces, la próxima vez que se enfrente a un problema de matemáticas, pregúntese: "¿Es posible?" Enfrentar la imposibilidad puede brindarle una comprensión más profunda de lo que es posible. Al hacerlo, incluso puede crear nuevas áreas de matemáticas.
Ejercicios
1. Halla el área de un triángulo con longitudes de lados 46, 85 y 38.
2. Sea... Encuentra tal todo, y en el cual ...
3. Encuentre un cuadrado completo en el que todos sus números constituyentes pertenezcan al conjunto {2, 3, 7, 8}.
Respuestas
respuesta 1
. , , . : 85 38 46. , - .
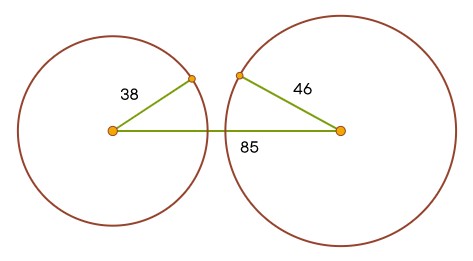
- -. !

- -. !
Respuesta 2
. , , , (d) (2).
Respuesta 3
, . 0, 1, 4, 5, 6 9. . 2, 3, 7 8, , .
Publicidad
Sean cuales sean sus necesidades, los servidores asequibles y fiables siempre son bienvenidos . Incluso para cálculos matemáticos complejos, la configuración máxima es de 128 núcleos de CPU, 512 GB de RAM, 4000 GB de NVMe.
