🕝 🤯 🖋️ Cómo confrontar a matemáticos y especialistas en ML con la ayuda de un hackathon, y quién ganará entonces 👼 👩🏿‍🤝‍👩🏼 〽️

Introducción

Este artículo trata sobre cómo nosotros, junto con la subsidiaria de Rosneft, Samaraneftekhimproekt, y la Universidad Federal de Kazán, celebramos el Hackathon of Three Cities en septiembre de 2020, donde invitamos a los estudiantes a resolver el problema clásico de la correlación sísmica de los horizontes reflectantes. Estos son los desafíos a los que se enfrentan a diario los profesionales de la sísmica de todo el mundo. Para los participantes, se decidió presentar la tarea como “la tarea de encontrar el camino óptimo” para no asustar a los estudiantes con palabras terribles. En el artículo, le contaremos más sobre el problema y analizaremos soluciones interesantes de los participantes. Será emocionante tanto para el modelado matemático aplicado como para el aprendizaje automático y los analistas de datos.

Parte organizativa

Describimos detalles interesantes de la organización de un hackathon en línea en tres ciudades en un artículo sobre vc.ru - Oil and Hackathon. Un maratón no se trata solo de correr .

Solo mencionaremos que para el formato en línea hemos elegido el servicio Discord y dejaremos un enlace a las reglas del hackathon (enlace en el sitio de Boosters ).

Formulación del problema

En la exploración sísmica, existe el concepto de "horizonte sísmico reflectante": es una onda reflejada, estable en dinámica y área de propagación, que corresponde a un cierto límite geológico. Procesando correctamente los datos sísmicos de campo y reconociendo (dicen los expertos en prospección sísmica - "interpretando") los horizontes sísmicos, es posible determinar la profundidad de su ocurrencia con una precisión de 5-10 metros. Una vez determinadas las profundidades, es posible, junto con los geólogos, vincular estos horizontes a una escala geocronológica ( escala geocronológica - Wikipedia ) y reconocer sus contrapartes más pequeñas. Y luego decida: entre qué horizontes pueden encontrarse las trampas con petróleo, cómo se ve el relieve del modelo estructural del campo, etc.

imagen

Secciones verticales del cubo sísmico y horizontes sísmicos reflectantes reconocidos

En la práctica, los horizontes se identifican capa por capa en las secciones sísmicas del cubo sísmico, tanto manualmente, usando una matriz (dicen los expertos en sísmica - "buceando") una gran cantidad de puntos de referencia, y usando procedimientos de búsqueda automatizados y semiautomatizados ... Por supuesto, una solución de alta calidad para el problema de interpretar los horizontes sísmicos utilizando software tiene una gran demanda y puede reducir significativamente el tiempo empleado por los especialistas en prospección sísmica.

Al mismo tiempo, el estudio de fuentes ( horizontes de mínimos cuadrados con pendientes locales y correlaciones de múltiples cuadrículas, Waveform Embedding: selección automática de horizontes con deep learning no supervisado) muestra que los algoritmos y soluciones desarrollados se basan en una pequeña cantidad de enfoques matemáticos, por lo que decidimos intentar atraer a los estudiantes con su conciencia aún no nublada por la investigación científica y ofrecerles este problema en forma de problema de encontrar el camino óptimo en una superficie compleja.

Como resultado, el problema se formuló de la siguiente manera: construcción de una trayectoria de movimiento sobre una superficie compleja, pasando por puntos dados y satisfaciendo las condiciones para un mínimo de alguna funcional, dependiendo de la longitud de la trayectoria y sus ángulos (gradientes).

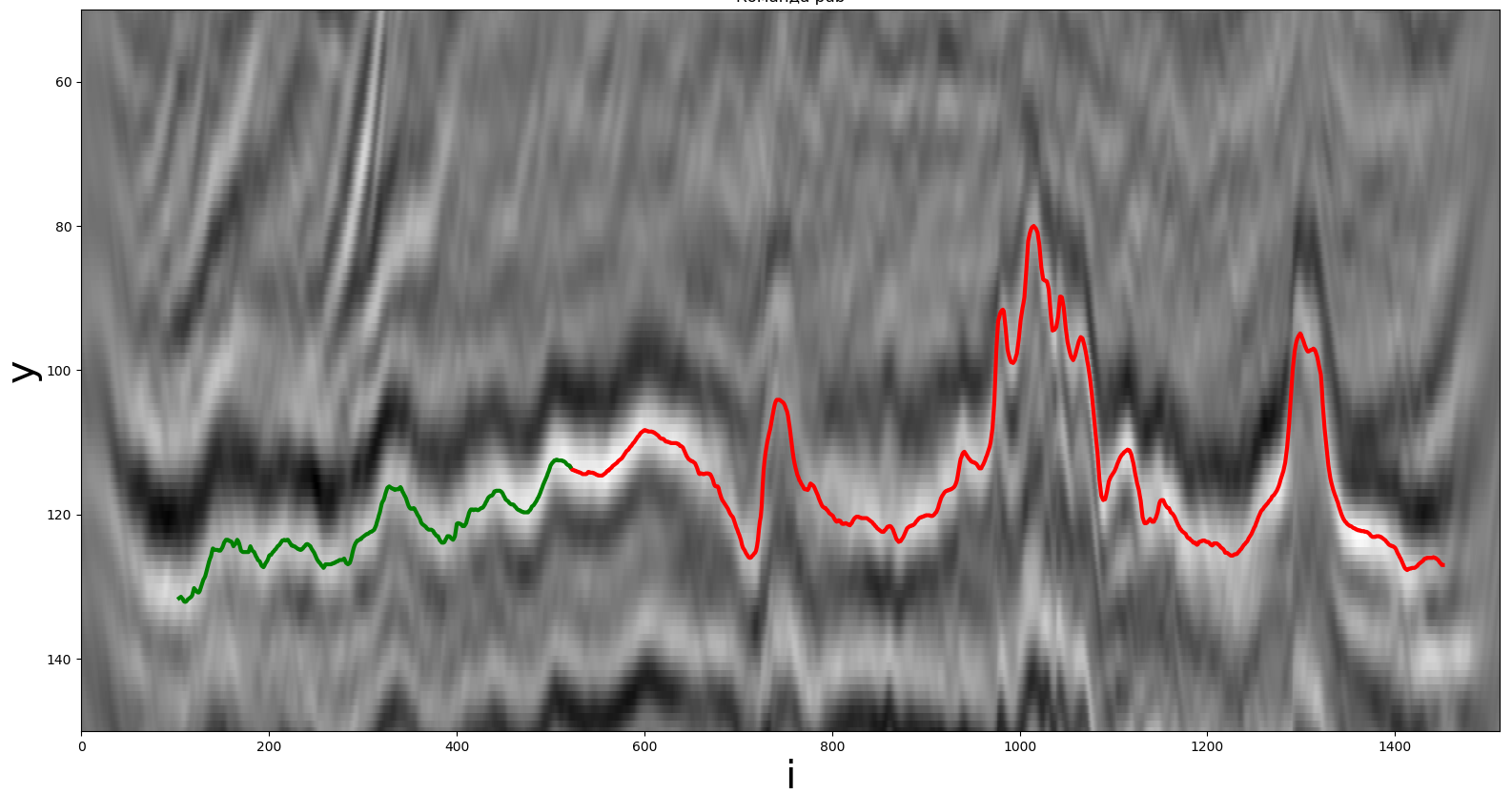
imagen

Un ejemplo de una porción de la sección sísmica original para construir un horizonte. La línea verde es la parte conocida anteriormente, la línea roja es la parte requerida.

Los participantes de la competencia debían encontrar una solución en 12 horas que les permitiera continuar su camino por la trayectoria óptima en la parte oculta del conjunto de datos. Hubo 20 intentos para validar la solución, el participante con el valor mínimo de métrica ganó.

Descripción detallada de los datos

, :

. , [x,y] z(x,y) .
(x,y) L1 L2. x, hor_1, …, hor_4.
L2 4 (1, 2, 3, 4), L1 – 3 (1, 3, 4). 2- L1 (40%). 60% .

, – 2 .

-, hor_2 L1. L2 L1. . , , .

A lo largo de la competencia, las clasificaciones se construyeron en función de los valores métricos de la parte pública de los datos de la prueba. Una vez finalizada la competencia, se recalculó el valor de la métrica en la parte privada y se actualizó la clasificación. Esto es importante para obtener soluciones sostenibles, es decir, no solo adaptadas a los datos públicos, sino también capaces de mostrar un resultado comparable en los datos privados. Resultó que esto no se hizo en vano, y después de la evaluación de calidad final, la clasificación cambió.

Se utilizó la siguiente métrica para cuantificar los resultados obtenidos:

F (\hat{y}, \hat{z}) = \sqrt{\sum_{i = 0}^{N} ({\hat{y}}_{i}^{p r e d} - {\hat{y}}_{i}^{e t a l o n}) + {(\hat{z} (i, y_{i}^{p r e d}) - \hat{z} (i, y_{i}^{e t a l o n}))}^{2}}

$F\left (\widehat{y},\widehat{z} \right ) = \sqrt{\sum_{i=0}^N\left(\widehat{y}_{i}^{pred} -\widehat{y}_{i}^{etalon} \right)+\left(\widehat{z}\left(i,y_i^{pred}\right) - \widehat{z}\left(i,y_i^{etalon} \right) \right)^2}$

donde:

N es la dimensión del horizonte requerido;

y_{i}^{p r e d}

${y}_{i}^{pred}$ - coordenadas del horizonte obtenidas mediante el algoritmo,

i \in \bar{0, N}

$i\in\overline{0,N}$ ;

y_{i}^{e t a l o n}

${y}_{i}^{etalon}$ - coordenadas del horizonte de referencia;

\hat{z} (i, y_{i})

$\widehat{z}\left(i,y_i\right)$ - valores del mapa de superficie en un punto con coordenadas i, yi;

{\hat{y}}_{i} = \frac{y_{i}}{h e i g h t}

$\widehat{y}_i = \frac{y_i}{{height}}$ , donde la altura es el valor máximo posible de la coordenada y del mapa de superficie;

\hat{z} (i, y_{i}) = \frac{z (i, y_{i})}{m a x (z)}

$\widehat{z}\left(i,y_i\right) = \frac{z\left(i,y_i \right)}{{max \left(z \right)}}$ donde max (z) es el valor más grande del mapa de superficie.

Implementación de métricas en Python

def score(true, submission, all_data):
   #true – pandas.Dataframe    ;
   #submission - pandas.Dataframe   , 
   #;
   #all_data - numpy.ndarray    
   all_data = all_data.astype('float64')
   #    
   max_z = abs(all_data).max()
   #   
   y_pred = submission.loc[idx.index.values].y.values.astype('int')
   #  
   y_true = true.y.astype(int)
   #     
   z_pred = all_data[true.index.values.astype(int), y_pred.astype(int)]
   #     
   z_true = all_data[true.index.values, y_true]
   #   
   y_err = ((y_pred - y_true)/3000)** 2
   z_err = ((z_pred - z_true)/max_z) ** 2
   #     
   total_err = np.sqrt(np.sum(y_err + z_err))
   return total_err

Qué métodos utilizaron los equipos

El problema se seleccionó inicialmente de modo que pudiera resolverse de varias formas: directa e inversa (utilizando métodos matemáticos clásicos y métodos de aprendizaje automático, respectivamente).

Desde el punto de vista del aprendizaje automático, el problema se puede resolver mediante dos métodos:

1) Construcción de regresión

mediante pares de puntos conocidos (

x_{i}, y_{i}

$x_i,y_i$ ), puede construir un mapeo

f : ϕ (x_{i}) \mapsto y_{i}

$f:\phi \left(x_i \right)\mapsto y_i$ minimizando la función de pérdida L.

ϕ (x_{i})

$\phi \left(x_i \right)$ - descripción indicativa del i-ésimo punto.

Por ejemplo,

ϕ : x_{i} \mapsto x_{i}

$\phi : x_i \mapsto x_i$ o

ϕ : x_{i} \mapsto (x_{i}, x_{i}^{2}, x_{i} \cdot x)

$\phi : x_i \mapsto \left( x_i,x_i^2,x_i \cdot x \right)$

La función de pérdida puede ser la función de error inicial del enunciado del problema o una función más simple, por ejemplo, la desviación estándar de las rutas construidas y originales:

\frac{1}{N} \sum_{i = 0}^{N} {(y_{i} - {\hat{y}}_{i})}^{2}

$\frac{1}{N} \sum_{i=0}^N \left( y_i - \widehat{y}_i \right)^2$

Se pueden usar muchos métodos populares de aprendizaje automático para construir el mapeo f : comenzando con regresión polinomial, atravesando un bosque aleatorio y redes neuronales profundas.

Varios equipos han adoptado este enfoque utilizando como

ϕ

$\phi$ red neuronal convolucional o completamente conectada, y como f - red neuronal o procesos gaussianos.

2) Segmentación semántica

imagen

Un ejemplo de segmentación semántica

El problema original se puede resolver como un problema de visión por computadora. Los puntos (x, y) se consideran píxeles de la imagen, donde la imagen completa es el conjunto de datos completo y el "brillo" del píxel (x, y) es el valor z (x, y). Para construir una ruta, debe asignar una de las clases a cada píxel: 0 o 1. La parte de la imagen que está debajo de la ruta o la incluye pertenece a la clase 0, y el resto, a la clase 1. Una solución doméstica para este problema es una red neuronal totalmente convolucional U-Net, en una entrada que recibe una parte (parche) de la imagen original y genera una matriz del mismo tamaño, que consta de ceros y unos, que denota las clases de los píxeles correspondientes.

Además de las técnicas de aprendizaje profundo, también puede utilizar técnicas clásicas de procesamiento de imágenes y visión por computadora, como el relleno Flood para la segmentación de imágenes. Esto fue hecho por uno de los participantes, preprocesando así la imagen para una aplicación adicional de algoritmos para encontrar el camino más corto.

Desde el punto de vista de los métodos matemáticos clásicos , el problema propuesto es un problema de optimización clásico, y observamos intentos de resolverlo mediante los siguientes grupos de métodos:

, ;

. y , y, .
, ;

$y_i$ .
, .

, .

Primero, analicemos las decisiones de los participantes.

Métodos de aprendizaje automático:

una de las soluciones fue una red neuronal convolucional autorregresiva que produce un número real: el valor de la ruta.

{\hat{y}}_{i}

$\widehat{y}_i$ para el i-ésimo paso. Los parches de 32x32 píxeles de la imagen original se enviaron a la entrada de la red neuronal. Como una función

ϕ

$\phi$ Para la extracción de características, se utilizó la red neuronal convolucional previamente entrenada ResNet34. La representación de características obtenida por esta red neuronal se combinó con los valores de esta ruta de los 32 pasos anteriores. Para predecir otros 32 pasos, se utilizaron predicciones de redes neuronales anteriores como valores de horizonte anteriores. La red neuronal se entrenó mediante una modificación del descenso del gradiente estocástico de Adam con una disminución exponencial en el paso del optimizador a medida que se entrena. Para el entrenamiento, la desviación absoluta media se minimizó (los experimentos con la desviación estándar dieron peores resultados). Para evitar el sobreajuste, se utilizó un Dropout, es decir, la puesta a cero aleatoria de una parte de las neuronas. Se necesitaron unos 10 minutos para entrenar la red neuronal, 20 pases completos sobre todo el conjunto de datos y 720 pasos del optimizador.

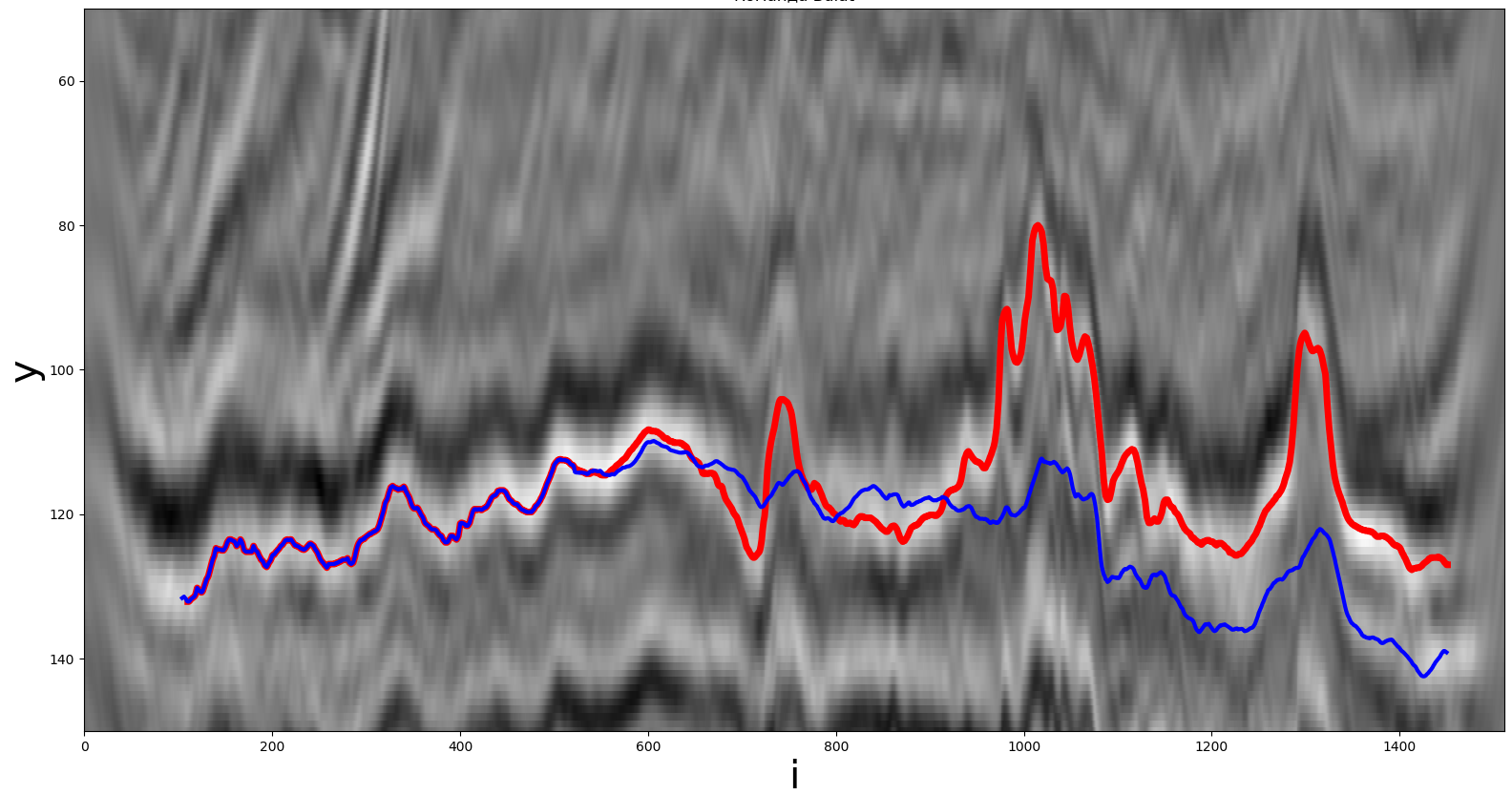
imagen

Una solución obtenida mediante una red neuronal convolucional. La línea roja es el camino real, la línea azul es la que recibe el participante.

La predicción de la red neuronal tarda aproximadamente 1 minuto en una CPU AMD Threadripper 2950x y una GPU Nvidia GTX 1080 Ti.

El resultado de la red neuronal (métrica) es 5,71 en la clasificación pública. También se hicieron experimentos para reemplazar la red neuronal convolucional por una recurrente, pero su resultado fue peor. Como resultado, se utilizaron métodos clásicos de matemática computacional como solución final.

Además de las soluciones terminadas, los participantes también compartieron sus ideas, que no lograron implementar debido al ajustado marco temporal de la competencia y la complejidad computacional de sus ideas. Algunos de ellos intentaron aplicar redes neuronales, pero después de pasar la mayor parte de su tiempo, pasaron a algoritmos más simples y eficientes o incluso a la fuerza bruta y las reglas, que finalmente dieron el mejor resultado y les dieron premios.

Además, una serie de soluciones interesantes se basan en conocimientos de otras disciplinas: por ejemplo, visión por computadora clásica y procesamiento de imágenes, teoría de grafos, análisis de series de tiempo. Uno de los equipos incluso planteó un desafío en términos de aprendizaje por refuerzo del que quizás haya oído hablar y se le ocurrió una solución, pero desafortunadamente no tuvo tiempo para implementarla.

Métodos matemáticos clásicos:

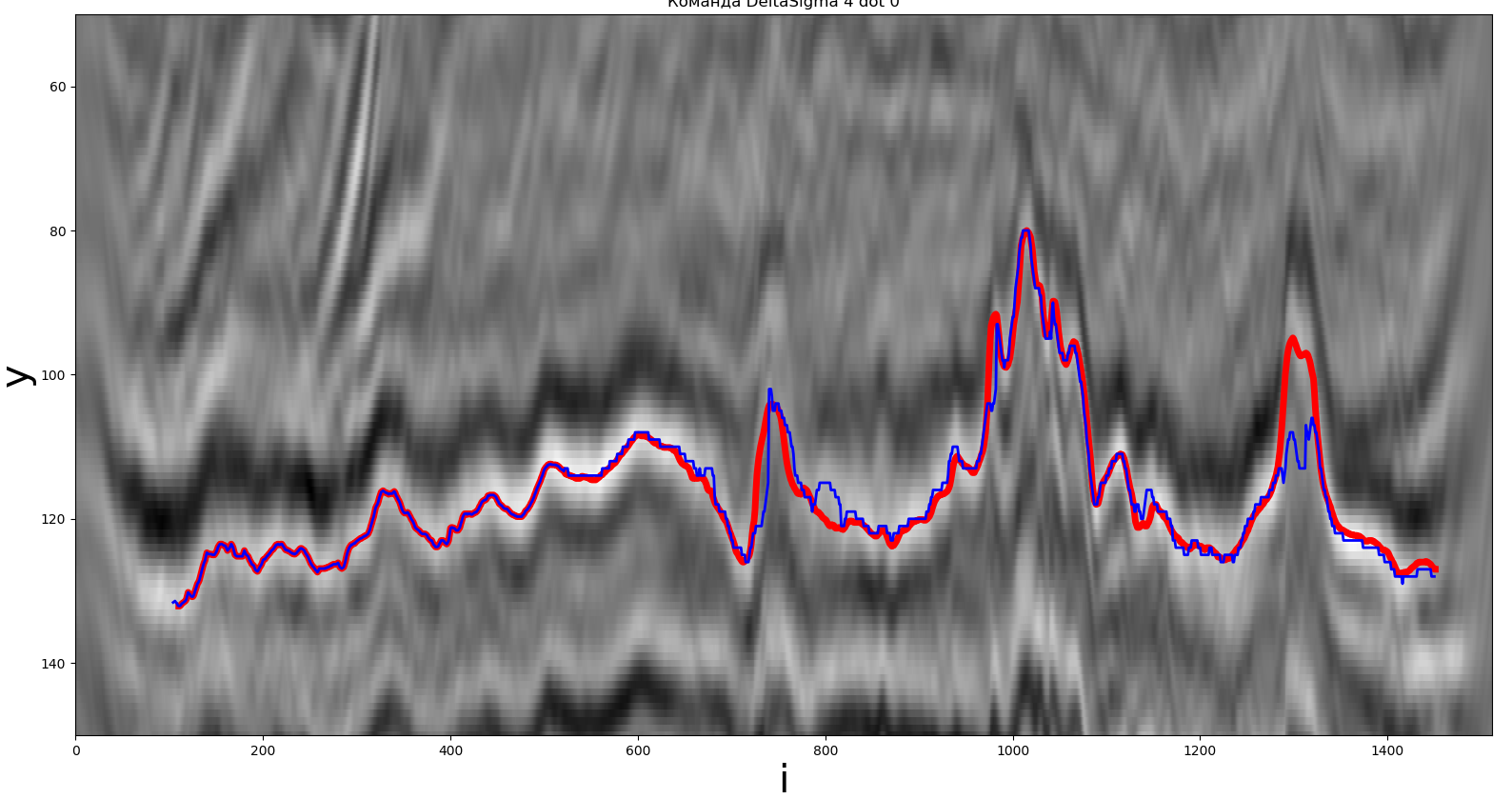
imagen

Una de las soluciones obtenidas por el método del extremo local. La línea roja es el camino real, la línea azul es la que recibe el participante.

Para este método, se utilizó un máximo local como extremo. El camino construido por los participantes está marcado en azul, el horizonte deseado está en rojo. A continuación se proporciona una descripción detallada.

y_{i + 1} = m i n | j - y_{i} |, \forall i \in \bar{0, N - 1}, j \in Ω,

$y_{i+1} = min \left| j-y_i \right|, \forall i \in \overline{0,N-1}, j \in \Omega,$

Ω = {m | z (i, m) > z (i, m - 1) \cap z (i, m) > z (i, m + 1), \forall m \in \bar{m_{1}, m_{2}}}

$\Omega = \left \{ m|z(i,m)> z(i,m-1) \cap z(i,m) > z(i,m+1), \forall m \in \overline {m_1,m_2} \right \}$ ,

m_{1} = m a x (1, y_{i} - s i z e_{y})

$m_1 = max(1,y_i - size_y)$ ,

m_{2} = m i n (h e i g h t - 1, y_{i} + s i z e_{y}

$m_2=min(height - 1,y_i + size_y$ ,

Donde:

h e i g h t

$height$ - el valor máximo posible de la coordenada y del mapa de superficie;

s i z e_{y}

$size_y$ - el tamaño de la ventana de búsqueda.

El método está implementado en Python. El tiempo de operación fue de aproximadamente 0.103 segundos, F (y, z) = 1.57,

s i z e_{y}

$size_y$ = 100.

Conclusión: el método es bastante sencillo de implementar, el tiempo de ejecución no supera los 0,1 segundos.

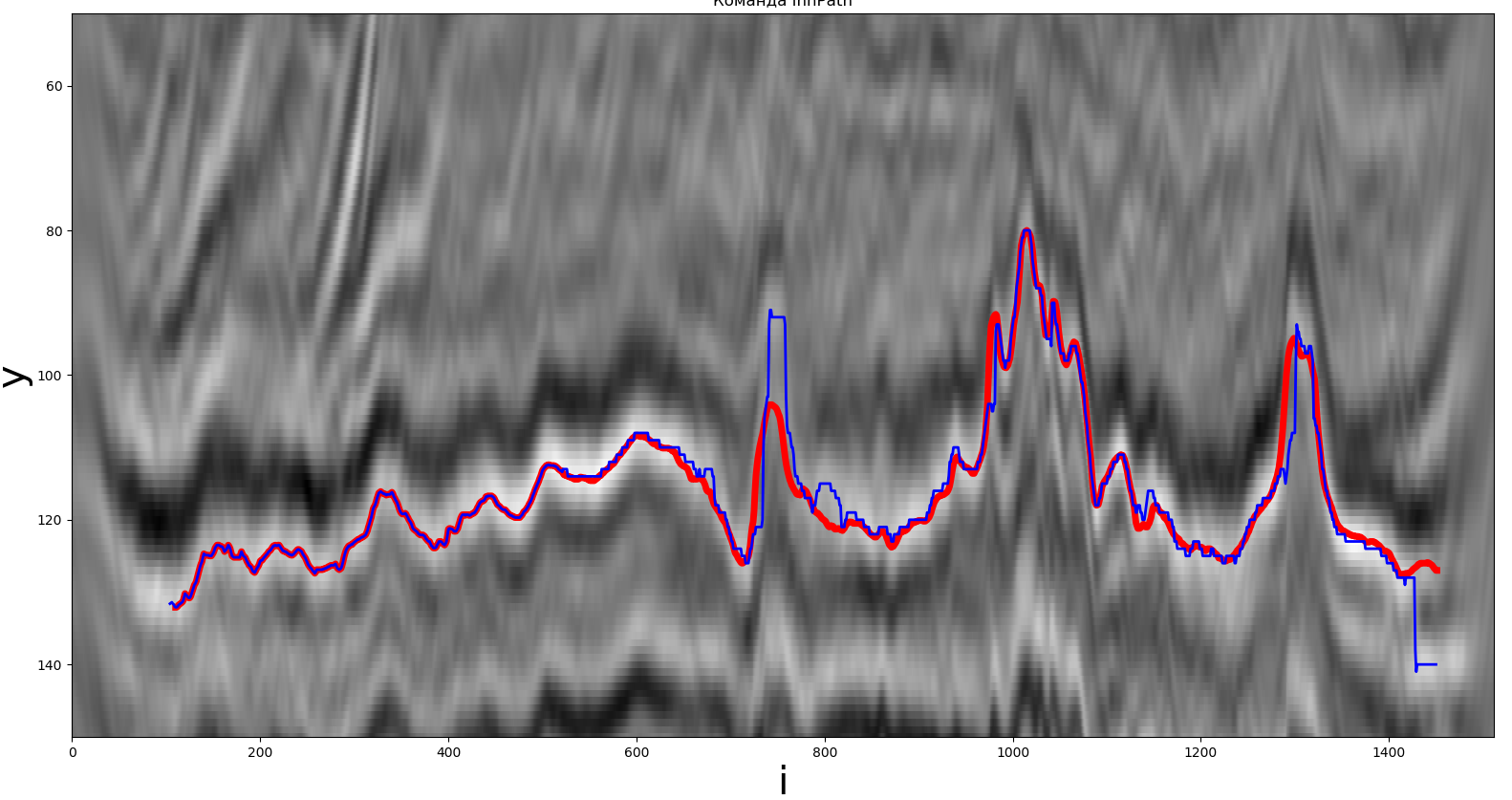
imagen

Una de las soluciones obtenidas por el extremo global. La línea roja es el camino real, la línea azul es la que recibe el participante.

Pasemos al siguiente grupo. Como antes, en este método, el máximo se utilizó como extremo.

y_{i} = a r g m a x (\frac{1}{s i z e_{x}} \sum_{j = 0}^{s i z e_{x} - 1} z (i + j, m))), \forall i \in \bar{0, N}, m \in \bar{m_{1}, m_{2}}

$y_i= {argmax}\left(\frac{1}{size_x} \sum_{{j=0}}^{{size_x-1}}z (i+j,m))\right), \forall i \in \overline {0,N}, m \in \overline{m_1,m_2}$ ,

m_{1} = m a x (1, y_{i} - s i z e_{y})

$m_1 = max(1,y_i - size_y)$ ,

m_{2} = m i n (h e i g h t - 1, y_{i} + s i z e_{y})

$m_2=min(height - 1,y_i + size_y)$ ,

donde:

altura es el valor máximo posible de la coordenada y del mapa de superficie;

s i z e_{x}, s i z e_{y}

$size_x,size_y$ - el tamaño de la ventana de búsqueda.

El método está implementado en Python. El tiempo de operación fue de aproximadamente 0,19 segundos, F (y, z) = 1,97,

s i z e_{x}

$size_x$ = 9,

s i z e_{y}

$size_y$ = 21.

Conclusión: el método es bastante simple de implementar, el tiempo de ejecución no supera los 0,2 segundos.

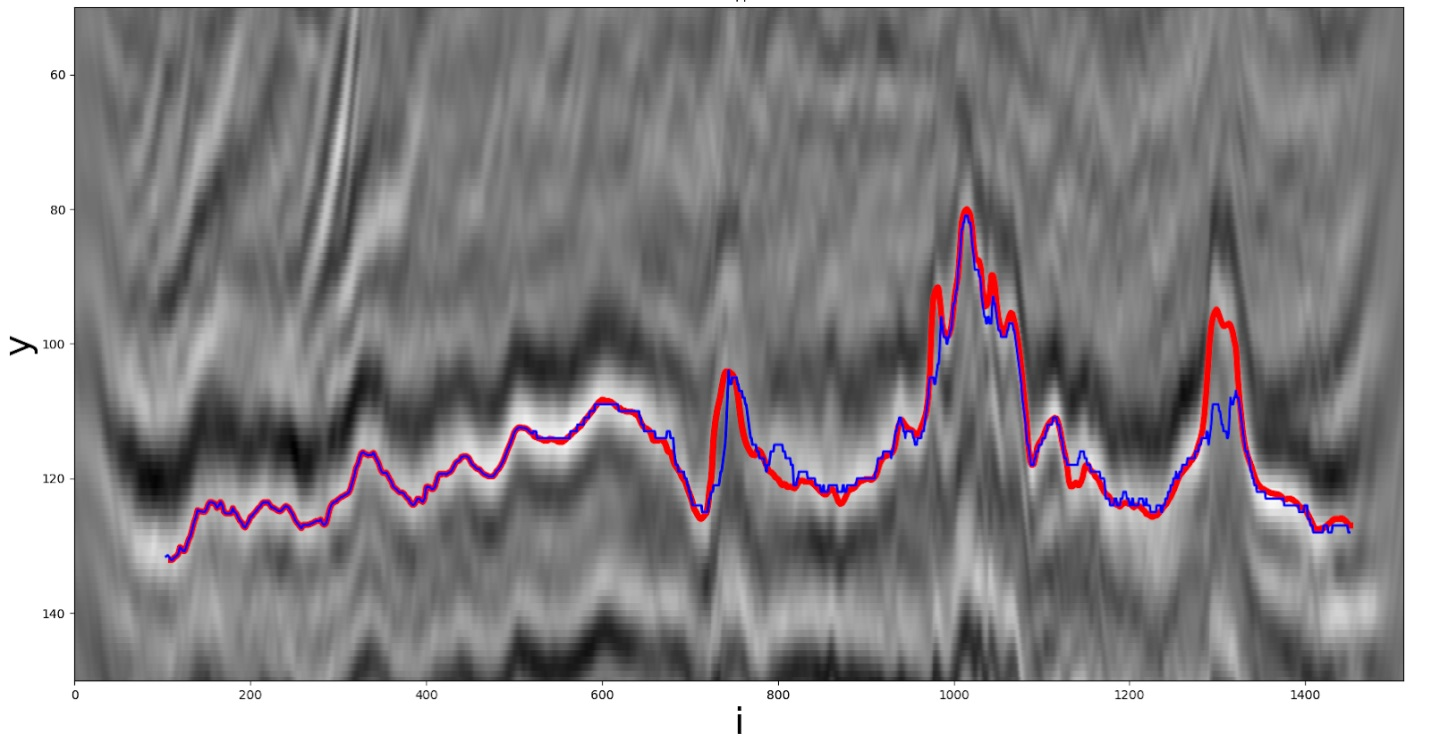
imagen

Una de las soluciones heurísticas. La línea roja es el camino real, la línea azul es la que recibe el participante.

Consideremos el último grupo de métodos. Como se mencionó anteriormente, la siguiente coordenada

y_{i} + 1

$y_i+1$ se busca por el mínimo de funcionalidad dentro de la ventana de búsqueda especificada.

A continuación se muestra una de las funcionalidades propuestas por los equipos. Desde un punto matemático, se ve así:

y_{i + 1} = m i n (\frac{(z (i, j) - z (i, y_{i}))^{2}}{m a x^{2} (z)} + α \frac{(j - y_{i})^{2}}{{h e i g h t}^{2}}), \forall i \in \bar{0, N - 1}, j \in Ω,

$y_{i+1}= {min}\left(\frac{(z(i,j)-z(i,y_i))^2}{max^2(z)} + \alpha \frac{(j-y_i)^2}{{height}^2}\right), \forall i \in \overline {0,N-1}, j \in \Omega,$

Ω = {m | z (i, m) > z (i, m - 1) \cap z (i, m) > z (i, m + 1), \forall m \in \bar{m_{1}, m_{2}}}

$\Omega = \left \{ m|z(i,m)>z(i,m-1)\cap z(i,m)>z(i,m+1), \forall m \in \overline {m_1,m_2} \right \}$

m_{1} = m a x (1, y_{i} - s i z e_{y})

$m_1 = max(1,y_i - size_y)$ ,

m_{2} = m i n (h e i g h t - 1, y_{i} + s i z e_{y})

$m_2=min(height - 1,y_i + size_y)$ ,

Donde:

h e i g h t

$height$ - el valor máximo posible de la coordenada y del mapa de superficie;

α

$\alpha$ - coeficiente responsable de la influencia del error en y sobre el valor del funcional;

s i z e_{y}

$size_y$ - el tamaño de la ventana de búsqueda;

m a x (z)

$max(z)$ Es el valor más alto del mapa de superficie.

El método se implementó en Python. El tiempo de operación fue de aproximadamente 0,12 segundos, F (y, z) = 1,58,

s i z e_{y}

$size_y$ = 50,

α

$\alpha$ = 15000,7.

Conclusión: el tiempo de ejecución del método no supera los 0,15 segundos.

Los métodos de los tres grupos mostraron resultados bastante similares en un conjunto de datos determinado. El valor más pequeño de la métrica (1,57) se logró mediante un método basado en la búsqueda de extremos locales de valores de superficie dentro de una ventana de búsqueda determinada.

Parte final

Desafortunadamente, al final del hackathon, casi todos los innovadores se habían ~~pasado al lado oscuro, se~~ volvieron a capacitar y se volvieron conservadores, es decir, comenzaron a enviar soluciones usando algoritmos clásicos ... y los conservadores ganaron.

Queríamos reunir a colaboradores de dos áreas: matemáticas computacionales y aprendizaje automático. Algunos están acostumbrados a trabajar con datos no estructurados de naturaleza desconocida, mientras que otros están acostumbrados a estudiar procesos físicos y construir modelos matemáticos a partir de ellos. Para aumentar la variedad de ideas y soluciones, describimos brevemente cómo se obtuvieron los datos. Ésta es una de las razones por las que la solución basada en métodos numéricos simples dio los mejores resultados. La segunda razón fue que para el hackatón de estudiantes, preparamos datos no muy "complejos" de un volumen pequeño, por lo que los métodos de aprendizaje automático laboriosos y modernos se ven perjudicados por alternativas más simples.

Creemos que esta es una lección excelente que ayudará a los participantes a establecer correctamente los problemas y elegir los mejores métodos para resolverlos. Es importante recordar que primero debes probar una solución simple, la denominada línea de base, quizás te permita lograr tu objetivo en poco tiempo.

Los participantes del Hackathon propusieron sus propios algoritmos para encontrar la ruta óptima en un gran conjunto de datos en relación con el problema de la interpretación cinemática sísmica automática, que actualmente se está resolviendo como parte del desarrollo de software corporativo en el campo de la geología y la sísmica. Las implementaciones de algoritmos más competitivas encontrarán su aplicación en el desarrollo e implementación de módulos de software para estos sistemas de software.

Estaremos encantados de verte en la final del maratón de competición de TI, que se celebrará online el 28 de noviembre. El programa incluye: premiación a los ganadores del concurso, presentación de la primera versión de la aplicación móvil para valoración expresa de la calidad del apuntalante. Asimismo, en el marco del evento, se organizarán mesas redondas sobre temas de actualidad "Gestión de proyectos de datos y DS" y "Visión por computadora". Representantes del Head of Data Science Alfa, CDO Megafon, Huawei, Head of CV X5 y otros compartirán casos interesantes No te pierdas toda la diversión ( IT Competition Marathon 2020 - Rosneft ).

Cómo confrontar a matemáticos y especialistas en ML con la ayuda de un hackathon, y quién ganará entonces

Introducción

Parte organizativa

Formulación del problema

Qué métodos utilizaron los equipos

Parte final

More articles: