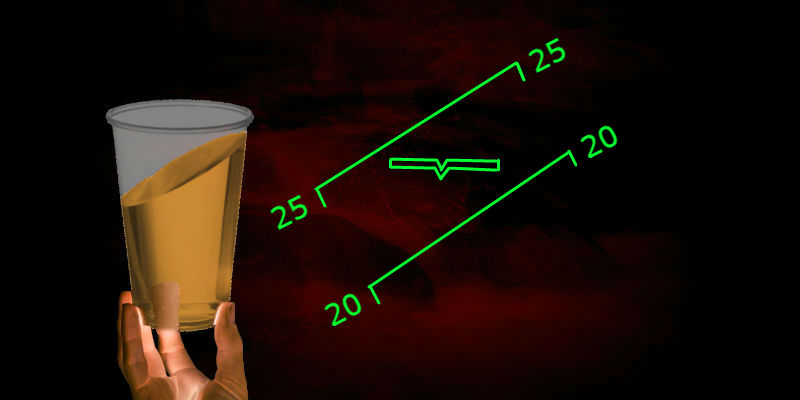
Objeto y alcance del horizonte artificial
Un horizonte artificial en el sentido estricto que se considera aquí es una visualización de la inclinación de un objeto en relación con la vertical local, que se utiliza para controlar su movimiento. La pendiente está definida por los valores de los dos ángulos de Euler, balanceo y cabeceo . Los marineros prefieren el sinónimo "corte" al término de aviación "cabeceo".
Términos relacionados con el horizonte artificial (pero no del todo sinónimos) en ruso: "horizonte artificial", "dispositivo de mando de vuelo". En inglés, se utilizan las expresiones "indicador de actitud" , "horizonte artificial" o "horizonte giroscópico" .
Técnicas de visualización conocidas
La mayor parte del trabajo para encontrar soluciones exitosas en el campo de la indicación de cabeceo y alabeo se ha realizado en interés de la aviación. Hay una explicación simple para esto: el piloto debe leer la información rápidamente y cualquier error en su percepción del espacio amenaza con volverse fatal.
La mayoría de las soluciones conocidas en el campo de la indicación de alabeo y cabeceo se basan en el uso de la silueta de un avión y un fondo especial. Características generales:
- el fondo se divide en dos partes, simbolizando el cielo y la tierra, por una línea que representa el horizonte;
- la silueta de la aeronave es una vista trasera simplificada, que contrasta en color con el fondo;
- el ángulo de balanceo lo determina el indicador como el ángulo entre la línea del horizonte simbólico y la línea que conecta las puntas de las alas de la silueta (generalmente hay una escala de referencia para una lectura precisa);
- el ángulo de paso se mide a lo largo de una escala perpendicular al horizonte condicional de acuerdo con la posición del punto de control en el centro de la silueta.

Los sistemas implementados en la producción en masa tienen una serie de soluciones comunes:
- la información viene dada por la posición relativa de la silueta y el fondo;
- el cambio en el ángulo de balanceo está asociado con el movimiento angular de la silueta con respecto al fondo;
- el cambio en el ángulo de inclinación está asociado con el desplazamiento lineal de la silueta con respecto al fondo.
Pero no es difícil adivinar que el movimiento relativo deseado se puede realizar de varias formas diferentes. Después de muchas pruebas y errores del siglo pasado, la evolución de la aviación ha dejado dos combinaciones viables:
1. Silueta fija, movimiento en rollo y fondo de cabeceo. Nombres utilizados: "indicación directa", "vista desde el avión al suelo", con menos frecuencia "indicación egocéntrica".
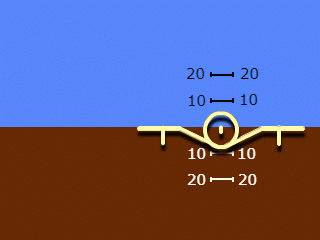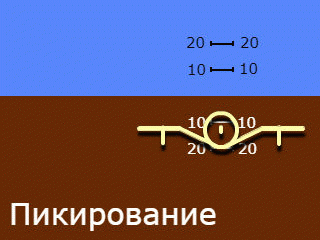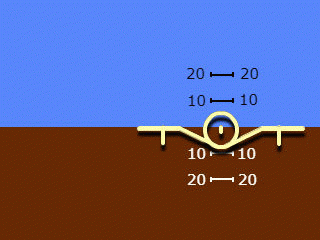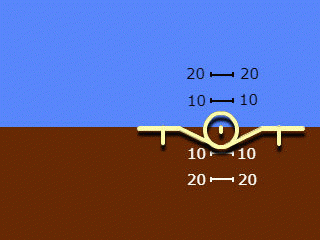
2. Una silueta que se mueve solo a lo largo del rollo, un fondo que se mueve solo a lo largo del campo. Nombres utilizados: "indicación inversa" y "vista desde el suelo al plano", con menos frecuencia "indicación geocéntrica".

Tenga en cuenta que los nombres de la cláusula 2 se aplican al sistema en su conjunto, pero reflejan solo el principio de indicación del ángulo de balanceo adoptado en él. La indicación del ángulo de inclinación en ambos sistemas utilizados es "recta" y "egocéntrica".
En los simuladores de vuelo existentes, como Microsoft Flight Simulator y Digital Combat Simulator , ambos tipos de pantallas se pueden ver en acción.
Vale la pena señalar que no todas las soluciones conocidas encajan en el patrón anterior. Para un ejemplo de ir más allá del marco designado, consideremos dos patentes de invención: RU 2561311 y RU 2331848.
La primera patente está dedicada al "Horizonte artificial con indicadores de cabeceo y alabeo espaciados en altura", sus autores: V.I. Putintsev y N.A.Lituev. Se toma el diagrama siguiente de la patente.

Si es necesario, puede encontrar una decodificación de designaciones y una descripción del trabajo en el texto de la fuente original.... En general, la idea de la invención es bastante simple: la idea de una "vista desde el suelo a un avión" se realiza tanto en balanceo como en cabeceo ("geocentrismo completo"), pero la indicación se divide en dos componentes independientes.
La segunda invención tiene un nombre más complejo: "Dispositivo de mando de vuelo para indicación lógica de posición y control de una aeronave en el espacio". Autores de la patente: A.P. Plentsov y N.A. Zakonova. La idea de indicación de cabeceo y balanceo es bastante inusual aquí.
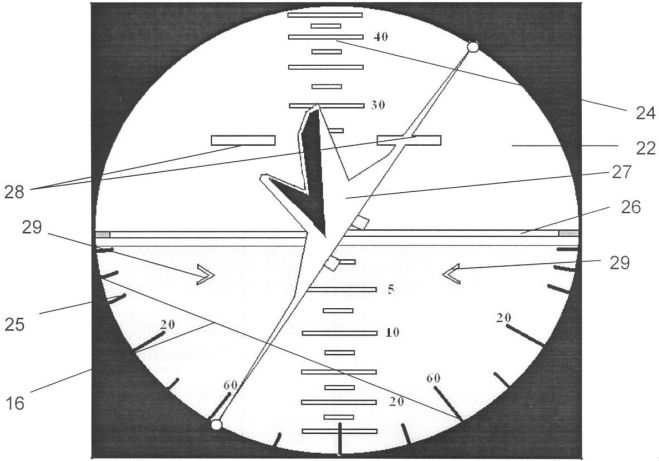
En la patente se proporciona una explicación de las designaciones del circuito, una descripción del dispositivo, una comparación con los circuitos analógicos y adicionales con ligeras diferencias en el diseño .
Una cosa en común con la invención anterior es el concepto de geocentrismo para ambos canales. Al mismo tiempo, el horizonte artificial tiene un solo "símbolo de avión", como en los modelos existentes, pero ya no es una silueta, sino un modelo tridimensional, un "modelo volumétrico". Si el movimiento de balanceo resulta ser similar al implementado en la indicación "reversa", entonces el cabeceo y el salto en este dispositivo parecen originales.

Hay una serie de factores que frenan la innovación en el diseño de sistemas de visualización del mundo real. Por ejemplo, uno de los motivos razonables para el conservadurismo es el deseo de preservar la continuidad de las habilidades adquiridas por el operador, incluidas las habilidades para percibir información. Los juegos de ordenador pueden permitir mucha más creatividad, por ello, sin ahondar en un análisis comparativo de soluciones, tomaremos como base el invento que parezca más efectivo.
Requisitos de la solución
Antes de comenzar a escribir el código, definamos la tarea:
1. Es necesario escribir la función drawAttitude () , que dibuja el indicador de horizonte artificial mediante un lienzo basado en la invención de A.P. Plentsov y N.A. Zakonova
2. La función toma el contexto del lienzo , coordina el centro del indicador, los valores de los ángulos de balanceo y cabeceo en grados, el radio de la cara del indicador.
3. Los valores del ángulo de inclinación están limitados al intervalo de menos 30 a más 30 grados.
4. Los valores del ángulo de balanceo están limitados al intervalo de menos 45 a más 45 grados.
5. Si el valor del argumento va más allá de los especificados en la p. 3 y 4 límites el indicador muestra el valor permitido más cercano.
Creación de funciones
El código de función incluye las siguientes partes:
1. Verificación de los valores ingresados por exceder los límites.
2. Conversión de ángulos a radianes.
3. Escalar el tamaño característico del "diseño" y la fuente por el valor del radio del indicador.
4. Dibujo de los componentes:
a) Cuerpo indicador.
b) Maquetación.
c) Escalas de cabeceo y balanceo.
La función a continuación está escrita en este orden y sus partes están separadas por comentarios.
Código completo
index.html:
attitude.js:
<!DOCTYPE html>
<html>
<head>
<title>Attitude</title>
<script src="js/attitude.js"></script>
</head>
<body>
<canvas id="drawingCanvas" width="640" height="480"></canvas>
</body>
</html>attitude.js:
window.onload = function () {
let canvas = document.getElementById("drawingCanvas");
let context = canvas.getContext("2d");
let run = function () {
drawAttitude(context, 320, 240, 30 * Math.sin(performance.now() / 2000), 45 * Math.sin(performance.now() / 5000), 200);
}
let interval = setInterval(run, 1000 / 60);
};
drawAttitude = function (ctx, centreX, centreY, pitch, roll, radius = 100) {
// :
if (pitch > 30) pitch = 30;
if (pitch < -30) pitch = -30;
if (roll > 45) roll = 45;
if (roll < -45) roll = -45;
// :
roll *= Math.PI / 180;
pitch *= Math.PI / 180;
// "" :
let vehicleSize = radius * 0.8;
ctx.font = Math.round(radius / 8) + "px Arial";
// :
ctx.lineWidth = 2;
ctx.strokeStyle = "Black";
// :
ctx.beginPath();
ctx.arc(centreX, centreY, radius, 0, Math.PI, false);
ctx.fillStyle = "Maroon";
ctx.stroke();
ctx.fill();
// :
ctx.beginPath();
ctx.arc(centreX, centreY, radius, 0, Math.PI, true);
ctx.fillStyle = "SkyBlue";
ctx.stroke();
ctx.fill();
//"":
ctx.beginPath();
//:
let topSideIsVisible = (pitch >= 0);
ctx.strokeStyle = topSideIsVisible ? "Orange" : "Brown";
ctx.fillStyle = topSideIsVisible ? "Yellow" : "Red";
ctx.lineWidth = 3;
//
// 4 , ,
// :
ctx.moveTo(centreX, centreY - Math.sin(pitch) * vehicleSize / 2);
ctx.lineTo(centreX + vehicleSize * Math.cos(roll), centreY + vehicleSize * Math.sin(roll) * Math.cos(pitch));
ctx.lineTo(centreX, centreY - 2 * Math.sin(pitch) * vehicleSize);
ctx.lineTo(centreX - vehicleSize * Math.cos(roll), centreY - vehicleSize * Math.sin(roll) * Math.cos(pitch));
ctx.lineTo(centreX, centreY - Math.sin(pitch) * vehicleSize / 2);
ctx.stroke();
ctx.fill();
// :
// :
ctx.beginPath();
ctx.strokeStyle = "Black";
ctx.fillStyle = "Black";
ctx.lineWidth = 1;
//:
ctx.fillText(30, centreX - radius * 0.28, centreY - vehicleSize + radius / 20);
ctx.fillText(20, centreX - radius * 0.28, centreY - vehicleSize * 0.684 + radius / 20);
ctx.fillText(10, centreX - radius * 0.28, centreY - vehicleSize * 0.348 + radius / 20);
// - :
ctx.moveTo(centreX - radius / 10, centreY - vehicleSize);
ctx.lineTo(centreX + radius / 10, centreY - vehicleSize);
ctx.stroke();
ctx.moveTo(centreX - radius / 10, centreY - vehicleSize * 0.684);
ctx.lineTo(centreX + radius / 10, centreY - vehicleSize * 0.684);
ctx.stroke();
ctx.moveTo(centreX - radius / 10, centreY - vehicleSize * 0.348);
ctx.lineTo(centreX + radius / 10, centreY - vehicleSize * 0.348);
ctx.stroke();
// :
ctx.beginPath();
ctx.strokeStyle = "White";
ctx.fillStyle = "White";
//:
ctx.fillText(30, centreX - radius * 0.28, centreY + vehicleSize + radius / 20);
ctx.fillText(20, centreX - radius * 0.28, centreY + vehicleSize * 0.684 + radius / 20);
ctx.fillText(10, centreX - radius * 0.28, centreY + vehicleSize * 0.348 + radius / 20);
// - :
ctx.moveTo(centreX - radius / 10, centreY + vehicleSize);
ctx.lineTo(centreX + radius / 10, centreY + vehicleSize);
ctx.stroke();
ctx.moveTo(centreX - radius / 10, centreY + vehicleSize * 0.684);
ctx.lineTo(centreX + radius / 10, centreY + vehicleSize * 0.684);
ctx.stroke();
ctx.moveTo(centreX - radius / 10, centreY + vehicleSize * 0.348);
ctx.lineTo(centreX + radius / 10, centreY + vehicleSize * 0.348);
ctx.stroke();
// :
ctx.lineWidth = 2;
//+-15 :
ctx.fillText(15, centreX + radius * 0.6, centreY + radius * 0.22);
ctx.moveTo(centreX + 0.966 * 0.8 * radius, centreY + 0.259 * 0.8 * radius);
ctx.lineTo(centreX + 0.966 * 0.95 * radius, centreY + 0.259 * 0.95 * radius);
ctx.fillText(15, centreX - radius * 0.75, centreY + radius * 0.22);
ctx.moveTo(centreX - 0.966 * 0.8 * radius, centreY + 0.259 * 0.8 * radius);
ctx.lineTo(centreX - 0.966 * 0.95 * radius, centreY + 0.259 * 0.95 * radius);
//+-30 :
ctx.moveTo(centreX + 0.866 * 0.8 * radius, centreY + 0.5 * 0.8 * radius);
ctx.lineTo(centreX + 0.866 * 0.95 * radius, centreY + 0.5 * 0.95 * radius);
ctx.moveTo(centreX - 0.866 * 0.8 * radius, centreY + 0.5 * 0.8 * radius);
ctx.lineTo(centreX - 0.866 * 0.95 * radius, centreY + 0.5 * 0.95 * radius);
//+-45 :
ctx.moveTo(centreX + 0.707 * 0.8 * radius, centreY + 0.707 * 0.8 * radius);
ctx.lineTo(centreX + 0.707 * 0.95 * radius, centreY + 0.707 * 0.95 * radius);
ctx.moveTo(centreX - 0.707 * 0.8 * radius, centreY + 0.707 * 0.8 * radius);
ctx.lineTo(centreX - 0.707 * 0.95 * radius, centreY + 0.707 * 0.95 * radius);
ctx.stroke();
}El más difícil de entender es el código para dibujar el "diseño". Considérelo con más detalle. Como diseño, se decidió utilizar una figura plana simétrica en forma de flecha.
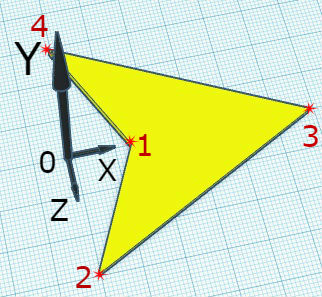
Las superficies superior e inferior del diseño se diferencian entre sí en los colores de contorno y relleno. La elección del esquema de color actual es la primera parte del código.
Luego viene la construcción del contorno de la figura.
La tarea más difícil es determinar las coordenadas de las proyecciones de los vértices de la figura en el plano YOZ . Esto es lo que resuelven las expresiones con funciones trigonométricas. Los vértices del código se recorren en el orden de su numeración en la figura.
La mayor parte del código está dedicada a escalas y firmas. Las marcas de escala tienen muchas diferencias: superior e inferior, izquierda y derecha, con y sin etiquetas. El impresionante número de líneas se debe a la escritura del código "individual" para cada elemento.
Las funciones trigonométricas de los ángulos correspondientes se utilizan para aplicar marcas de balanceo. Dado que los valores de los ángulos de cada etiqueta se conocen de antemano, los valores predefinidos de senos y cosenos se escriben en el código.
Es mejor evaluar la apariencia del indicador en dinámica. Vamos a mostrar las oscilaciones de cabeceo y balanceo utilizando la nueva función. Para la máxima variedad de posiciones, hagamos que las amplitudes de oscilación correspondientes a los límites del indicador y los períodos sean diferentes y mutuamente simples.
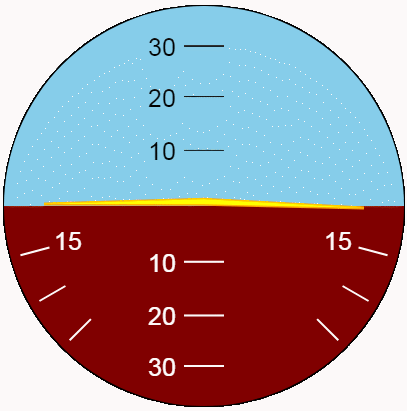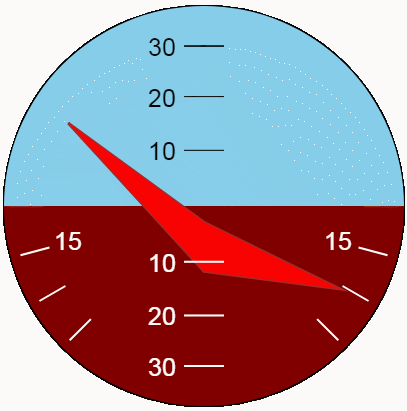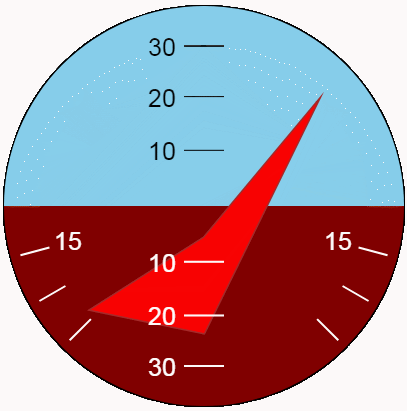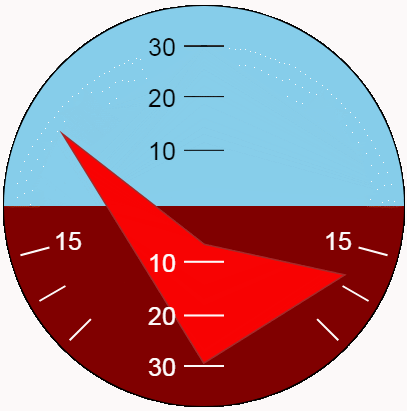
Conclusión
Estrictamente hablando, el código anterior para la visualización de balanceo y cabeceo debe llamarse una indicación "basada en" la invención de A. P. Plentsov y N. A. Zakonova. Se realizan algunas desviaciones de los esquemas originales para simplificar la tarea, otras para mejorar la implementación.
El indicador presentado está lejos de ser ideal en términos de diseño. Las limitaciones aceptadas de los valores mostrados no son óptimas según ningún criterio objetivo. Sin embargo, la tarea de crear un demostrador de tecnología interesante puede considerarse resuelta.