Control de manipuladores multienlace de un complejo robótico utilizando una red neuronal

Introducción

Al simular sistemas de control de movimiento para robots, se requiere resolver los problemas de cinemática y dinámica de sus actuadores. Hay un problema de cinemática inverso y directo. El problema directo de la cinemática es determinar la posición espacial y la orientación del punto característico, por regla general, de la herramienta de trabajo del robot manipulador mediante los valores conocidos de las coordenadas generalizadas. El problema inverso de la cinemática, como el problema directo, es uno de los principales problemas del análisis y síntesis cinemática. Para controlar la posición de los enlaces y la orientación de la herramienta de trabajo del manipulador, se hace necesario resolver el problema inverso de la cinemática.

La mayoría de los enfoques analíticos para resolver el problema de la cinemática inversa son bastante costosos en términos de procedimientos computacionales. Uno de los enfoques alternativos es el uso de redes neuronales. Datos de entrada. Considere un manipulador de tres enlaces con los parámetros que se muestran en la Tabla 1.

Tabla 1 - Parámetros DH para un manipulador de tres enlaces

En el entorno MatLab, utilizando Robotics Toolbox distribuido libremente, se construye un modelo de computadora de un manipulador de tres enlaces. A continuación se muestra un fragmento del script MatLab en el que asignamos a la matriz 'L' los valores de los parámetros, A, Alfa y D de la Tabla 1. Para nuestro modelo, estos son valores constantes y no cambian en el proceso de trabajo con el manipulador. Asignamos el parámetro Tetta a la variable 'initialPose_left', la posición inicial de nuestro manipulador. 

function [L,initialPose_left,baseL] =model3z 
%   
initialPose_left = deg2rad([0 0 0]); 
L(1) = Revolute('d', 0.2, 'alpha', pi/2, 'qlim', initialPose_left(1)+deg2rad([-90 +90]) ); 
L(2) = Revolute('d', 0, 'alpha', 0, 'a', 0.4, 'qlim', initialPose_left(2)+deg2rad([-20 +90]));   
L(3) = Revolute('d', 0, 'alpha', 0, 'a', 0.4, 'qlim', initialPose_left(2)+deg2rad([-90 +90])); 
% -178 +178 
baseL = [1 0 0 0;  
        0 1 0 0;  
        0 0 1 0;  
        0 0 0 1]; 

1 (. 1) . 

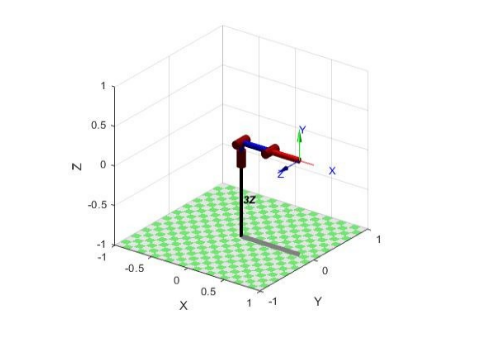
 Tetta, .  initialPose_left. 

. , . 

, .  

  . :

q – . 

%       
t1_min = L(1).qlim(1); t1_max = L(1).qlim(2);  
t2_min = L(2).qlim(1); t2_max = L(2).qlim(2); 
t3_min = L(3).qlim(1); t3_max = L(3).qlim(2); 
%     
t1 = t1_min + (t1_max-t1_min)*rand(N,1); 
t2 = t2_min + (t2_max-t2_min)*rand(N,1); 
t3 = t3_min + (t3_max-t3_min)*rand(N,1); 
Y = horzcat(t1, t2, t3);

, .  : 

:  x,y,z – . R – , . 

%    4x4 
T = zeros(4, 4, N); 
T(:, :, :) = leftArm.fkine(Y); %  ,       
%R = tr2rpy(T(1:3, 1:3, :), 'arm'); %      
R = tr2eul(T(1:3, 1:3, :)); %      
Tx = reshape(T(1, 4, :), [N 1]); %  - 
Ty = reshape(T(2, 4, :), [N 1]); 
Tz = reshape(T(3, 4, :), [N 1]); 
% scatter3(Tx,Ty,Tz,'.','r'); 
X = horzcat(Tx, Ty, Tz, R); %   

. 3.2.1  , 3000 . 

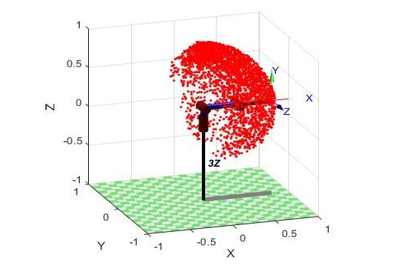
, 3000 . , X Y. 

, .

Keras Python. .

X_train, X_test, y_train, y_test = train_test_split(data_x, data_y, test_size=0.2,
random_state=42) 

« » . .

def base_model():
 model = Sequential()
 model.add(Dense(32,input_dim=6,activation='relu'))
 model.add(Dense(64,activation='relu'))
 model.add(Dense(128,activation='relu'))
 model.add(Dense(32,activation='relu'))
 model.add(Dense(3, init='normal'))
 model.compile(loss='mean_absolute_error', optimizer = 'adam', metrics=['accuracy'])
 model.summary()
 return model

, . . , , . , , .       KerasRegressor,  Keras.

clf = KerasRegressor(build_fn=base_model, epochs=500, batch_size=20,verbose=2)
clf.fit(X_train,y_train) 

.

res = clf.predict(X_test) 

99% , . 

3 , , , . . , . . - . , , , , .

%%    ,    
M=[-178:10:178]; %      -178   +178    10 
M_size=length(M); 
first_q=zeros(M_size, 3); 
T33 = zeros(4, 4, M_size); 
T34 = zeros(4, 4, M_size); 
first_q(:,1)=[deg2rad(M)]; %  q 
T33(:, :, :) = leftArm.fkine(first_q);%      ,   
R = tr2rpy(T33(1:3, 1:3, :), 'arm'); %      
Tx = reshape(T33(1, 4, :), [M_size 1]); %  - 
Ty = reshape(T33(2, 4, :), [M_size 1]); 
Tz = reshape(T33(3, 4, :), [M_size 1]); 
plot3(Tx,Ty,Tz) 
axis([-1 1 -1 1 -1 1]);hold on;grid on; 

XX = horzcat(Tx, Ty, Tz, R); %        
T34(:, :, :) = leftArm.fkine(q_new); %     ,   
Tx2 = reshape(T34(1, 4, :), [M_size 1]); %  - 
Ty2 = reshape(T34(2, 4, :), [M_size 1]); 
Tz2 = reshape(T34(3, 4, :), [M_size 1]); 
plot3(Tx2,Ty2,Tz2,'.') 
axis([-1 1 -1 1 -1 1])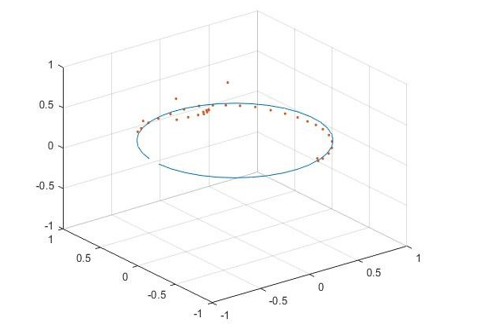 

. . , - . , . . «Programming by demonstration», . Matlab , – .