NaN todavía puede sorprenderte un poco

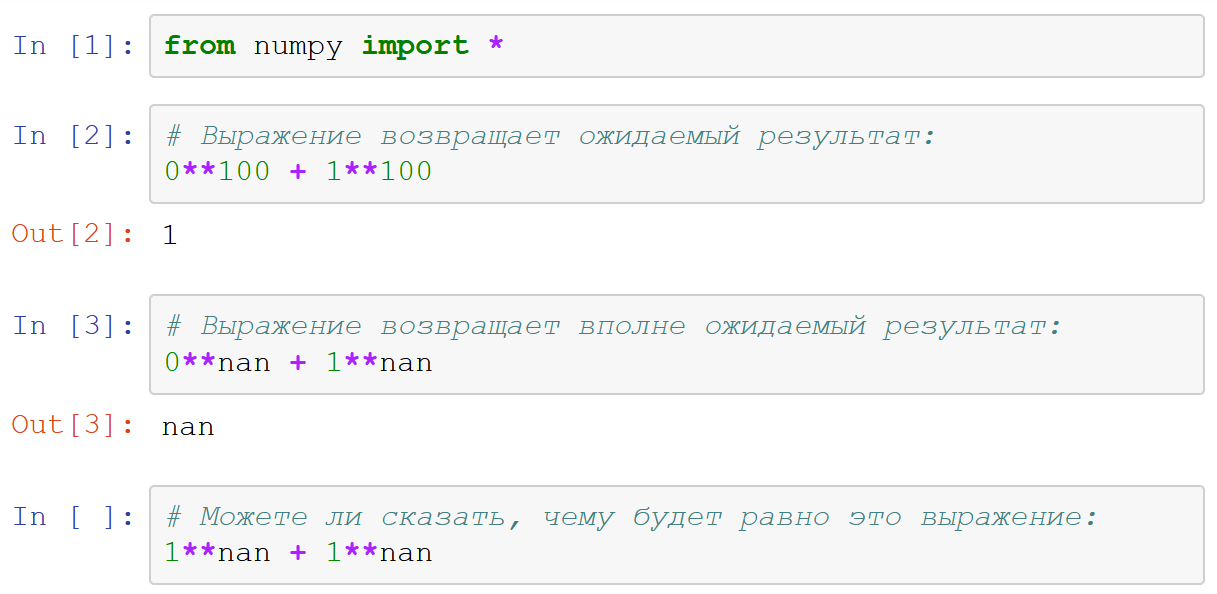
Al principio, pensé que esta era solo otra pregunta que podría hacerse en una entrevista. Probablemente, si usa su cerebro correctamente, puede adivinar cuál será el resultado. Recostándose en su silla, comenzó a pensar, a activar la lógica, a recordar algo en lo que basarse para razonar. ¡Pero en vano! De repente, resultó bastante obvio que no se podía encontrar la respuesta. ¿Pero por qué? ¿Qué necesitas entender para encontrarlo? ¿En matemáticas? ¿En un lenguaje de programación?



La respuesta debería ser NaN. Pero, ¿por qué no estoy seguro de esto? En todo momento, estaba seguro de que cualquier expresión que contenga NaN devolvería NaN. Bueno, quizás solo si divide NaN por cero; en este caso, se lanzará una excepción ZeroDivisionError . ¡Cien por ciento NaN!



Entro la expresión en una celda del bloc de notas:

>>> 1**nan + 1**nan
2.0

¿En efecto? Espere:

>>> arange(5)**nan
array([nan,  1., nan, nan, nan])

Es decir, por alguna razón, uno a la potencia NaN es uno, pero cero y todos los demás números a la potencia NaN son NaN. ¿Dónde está la lógica? ¿Qué pasa?



Así que vayamos de nuevo:

>>> 0**nan, 1**nan
(nan, 1.0)

¿Quizás simplemente no sospeché algo debido a la falta de una necesidad práctica de un conocimiento profundo de NaN? ¿O tal vez lo sabía, pero lo olvidé? O tal vez incluso peor: no lo sabía y lo olvidé.



Vamos a Wikipedia . Allí, este tema también se designa como un problema, pero no se explica de ninguna manera por qué todo está organizado de esta manera. Pero aprendí que:

>>> hypot(inf, nan)
inf

Aunque, al mismo tiempo:

>>> sqrt(inf**2 + nan**2)
nan

Eso, verás, también es un poco extraño.



Bien, de Wikipedia vamos a C99 en la página 182 y finalmente obtenemos una explicación lógica de por qué pow (x, 0) devuelve 1 para cualquier x , incluso para x igual a NaN:

>>> power(nan, 0)
1.0

Si la función $$$f(x)$ se eleva al poder $$$g(x)$ y donde $$$g(x)$ tiende a 0, entonces el resultado será 1, independientemente del valor $$$f(x)$...







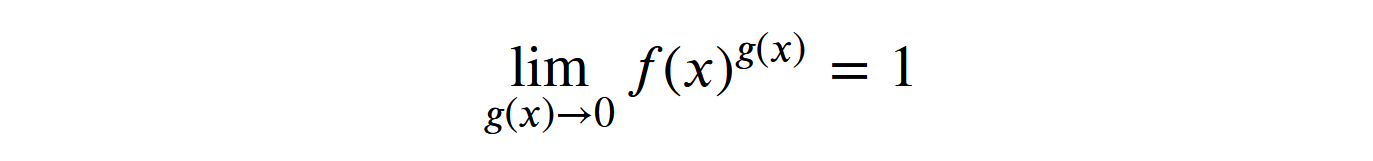
Y si el resultado no depende del valor numérico de la función$$$f(x)$, entonces 1 es un resultado válido, incluso para NaN. Sin embargo, esto todavía no explica por qué 1 elevado a la potencia de NaN es 1. Buscamos



otro C99 y en la página 461 no vemos ninguna explicación, solo el requisito de que pow (+1, y) debería devolver 1 para todo y , incluso igual Yaya. Todo.



Por otro lado, explicar por qué pow (NaN, 0) = 1 es preferible a pow (NaN, 0) = NaN todavía sugiere que NaN no debe tomarse literalmente como No-un-Número. ... Supongamos que, como resultado de algunos cálculos, obtenemos un número que excede el tamaño de la memoria asignada para este tipo de números, por ejemplo:

>>> a = pi*10e307
>>> a
inf

Como resultado, obtuvimos inf , qué es exactamente este número que no sabemos, pero aún así es una especie de número. Luego calculamos algo una y otra vez obtuvimos un número demasiado grande:

>>> b = e*10e307
>>> b
inf

La diferencia entre a y b devolverá NaN:

>>> c = a - b
>>> c
nan

La única razón por la que podemos pensar que c no es un número es porque no usamos cálculos precisos. Sin embargo, en c, debajo de NaN, todavía hay algún significado oculto. No sabemos cuál es este significado. Pero sigue siendo un número, y dado que es un número, no hay nada sorprendente en el hecho de que pow (1, NaN) = 1 .



¿Por qué entonces pow (0, NaN) = NaN ? El hecho es que si elevamos 0 a cualquier potencia, entonces realmente obtenemos cero. Excepto en un solo caso, cuando el grado es 0:

>>> 0**0
1

Debido a esto , existe ambigüedad en la expresión pow (0, NaN) con un valor de NaN específico. Por supuesto, la probabilidad de que 0 pueda ocultarse bajo NaN es extremadamente pequeña y se podría suponer que pow (0, NaN) = 0 . Sin embargo, es mejor ir a lo seguro, nunca se sabe a qué puede conducir esto. Quizás así es como razonaron cuando se crearon los estándares.



Ni siquiera sé qué más decir ... si supiste la respuesta de antemano, lo más probable es que te envidien, porque las áreas en las que ese conocimiento puede ser útil probablemente estén llenas de tareas interesantes. Y quizás viceversa. Escribe sobre ello en los comentarios.



PD Dado que NaN se refiere a números de punto flotante, puede ser una clave de diccionario:

>>> d = {0.1: 'a', nan: 'b'}
>>> d[nan]
'b'

¿Tiene sentido usar esto en la práctica? No creo que valga la pena.