🚇 🔊 🚥 ¿Existe paralelismo en un algoritmo arbitrario y cómo usarlo de la mejor manera? 🛌🏽 🐻 🧒

La paralelización del procesamiento de datos se utiliza actualmente principalmente para reducir el tiempo de cálculo al procesar simultáneamente datos en partes en muchos dispositivos informáticos diferentes y luego combinar los resultados. La ejecución en paralelo permite "pasar por alto" la ley fundamental formulada por Lord Rayleigh en 1871, según la cual (aplicada a la disipación de calor de los procesadores) su potencia de disipación de calor es proporcional a la cuarta potencia de la frecuencia del reloj del procesador (duplicar la frecuencia aumenta la disipación de calor 16 veces) y reemplazarla por una lineal de la cantidad de computadoras en paralelo, mientras se mantiene la frecuencia del reloj). Nada se da gratis: la tarea de revelar (generalmente oculto para el observador no iniciado, [1]) el potencial del paralelismo en los algoritmos no está en la superficie,y la eficacia de su uso (paralelismo), incluso más.

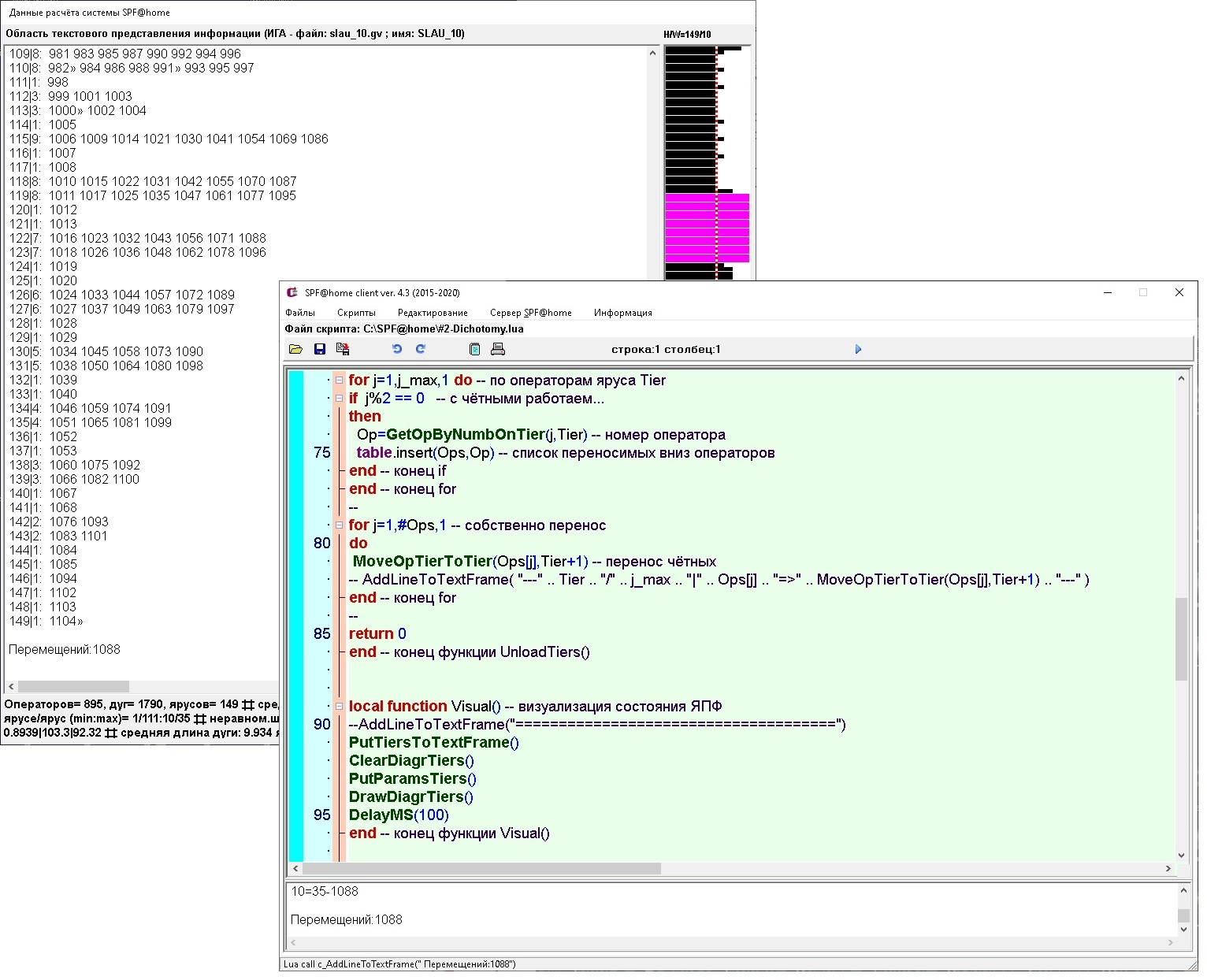
A continuación se muestra una ilustración del proceso de detección de paralelismo para el caso más simple de evaluar la expresión axb + a / c (a, b, c - datos de entrada).

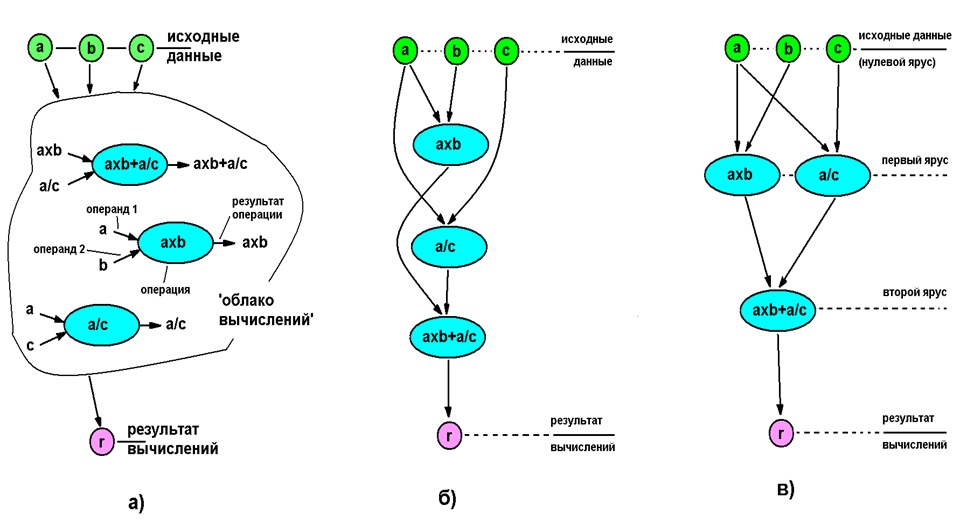
a) - "nube de operador" (la secuencia de ejecución no está definida), b) - ejecución completamente secuencial, no definida), b) - ejecución completamente secuencial, c) - ejecución paralela

, . ( ) ( – ., ). .1 “ ”, ( ) .

(- ), . , . () . NP- [2], ( ) ( -). , “ ” (Data Science).

AlgoWiki [3].

, , c ILP (Instruction-Level Parallelism, , EPIC (Explicitly Parallel Instruction Computing, ). , .

() ( , ). (). “ - ”, ( ) , – () ). , (- ).

( ) - (), [4]. ( ).

( ) O(N2) , N – ( ), ( ) . ( ). .. , . , .

, , .

. ax2+bx+c=0.

La figura muestra la forma paralela de niveles del algoritmo para resolver la ecuación cuadrática completa en números reales en la forma canónica (los números de los niveles de LPF se encuentran a la derecha) — - - ( )

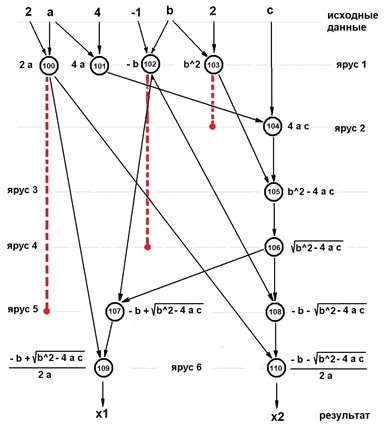
( “ ”, 6 4- ). ( ) – 1- 4, 2,3,4 - 5- 6 . , ( ) ( ) ! – ( ).

( ) , - D-F SPF@home. http://vbakanov.ru/dataflow/content/installdf.exe http://vbakanov.ru/spf@home/content/installspf.exe ( - http://vbakanov.ru/dataflow/dataflow.htm http://vbakanov.ru/spf@home/spf@home.htm).

La figura muestra el diagrama del complejo instrumental (* .set y * .gv - el archivo del programa y el archivo del gráfico de información del programa analizado, respectivamente, * .mvr, * .med - archivos de las métricas de los vértices y arcos del gráfico del algoritmo, respectivamente, * .cls, * .ops - archivos de parámetros de calculadoras y operadores de programa, respectivamente, * .lua - un archivo de texto en lenguaje Lua, que contiene métodos de reorganización — - (*.set *.gv – , *.mvr, *.med – , *.cls, *.ops – , *.lua – Lua,

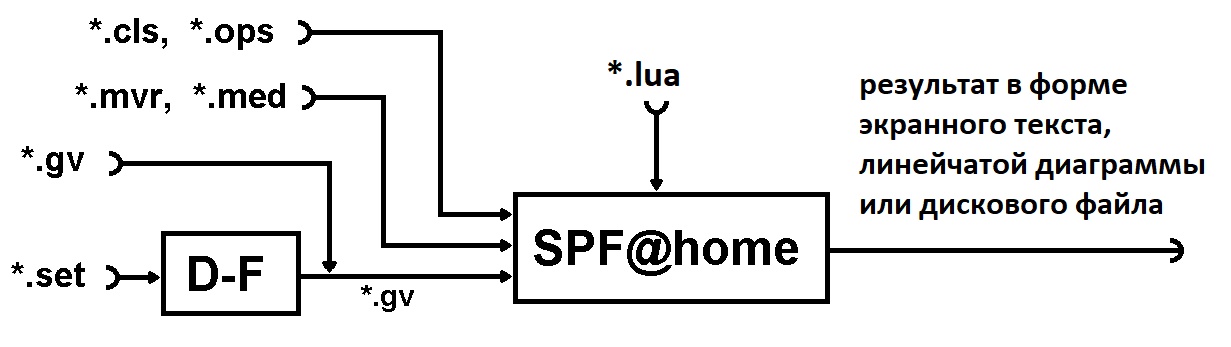
(set-) – gv- ( “ - ”, ( ) , – () ). , (- ).

() . “” .

Lua (Lua ANSI C, , - , ).

++, GUI Win’32- ( ) GIT-. ( ).

(Lua- “” API- SPF@home).

( D-F SPF@home ).

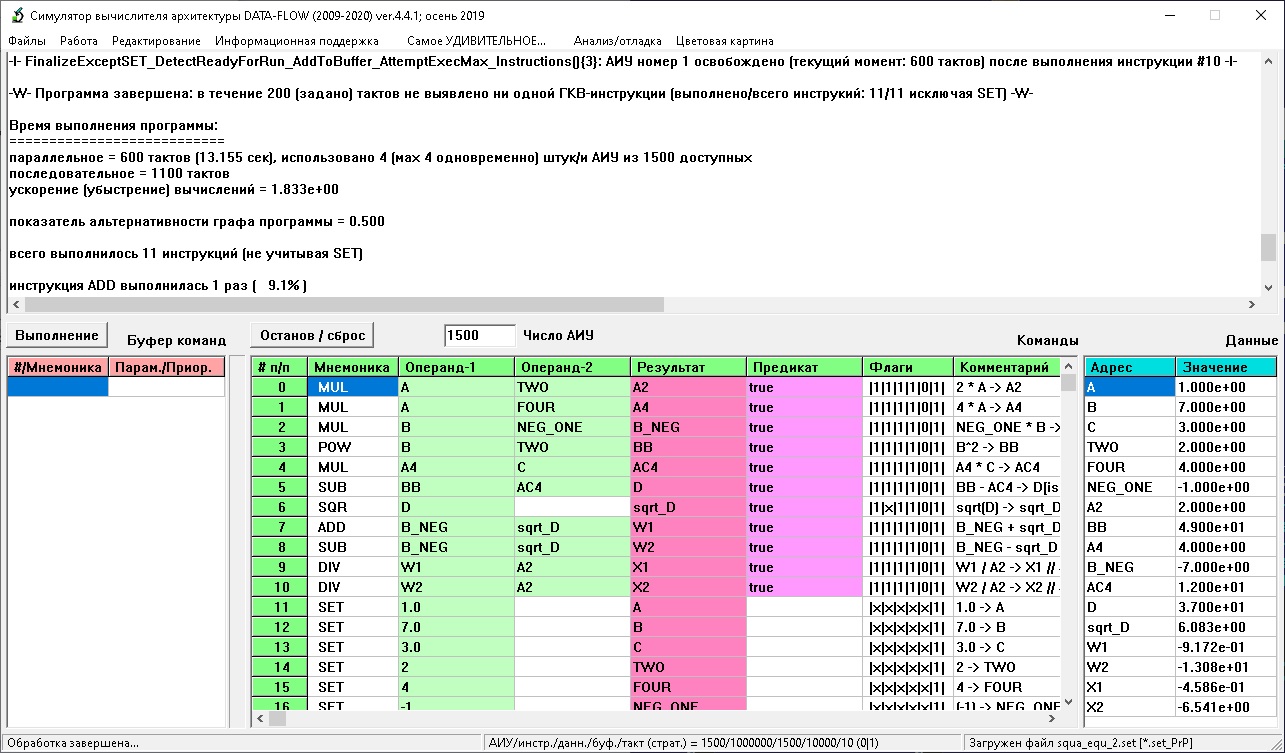
D-F (Data-Flow) , . 1 “Data-Flow” ( ), (), ; . - , , , “” . D-F , .

D-F , , . ( set- D-F, ):

, . D-F , - SPF@home. SPF@home gv- ( ), , Lua- ( API- , ):

CreateTiersByEdges("EdgesData.gv")  --     EdgesData.gv 
--    “”
-- CreateTiersByEdges_Bottom("EdgesData.gv")  --     EdgesData.gv 
--    “”
--
OpsOnTiers={} --   1D- OpsOnTiers 
for iTier=1,GetCountTiers() do --   
   OpsOnTiers[iTier]={} --  iTier-  2D- OpsOnTiers
   for nOp=1,GetCountOpsOnTier(iTier) do --       iTier  
      OpsOnTiers[iTier][nOp]=GetOpByNumbOnTier(nOp,iTier) --    nOp
end end --   for  iTier  for  nOp

gv- mvr med-, cls ops- . ( “-”, ) . , .

SPF@home “ ” , / ( ). med-.

, c ILP (Instruction-Level Parallelism, ), SPF@home .

.. Lua-, . ( ) :

I. “” ( ).

II. ( ).

III. .

( ) ; ( ).

, (, ) , , ( – ).

1) ( ) .

2) .

- . ( , , , ). “” API- “” ( , ).

“” ( ) ( ). “” “” ( ; “” ””).

( ) - “ ”, , “” . ( ). “” Windows- WinExec, ShellExecute CreateProcess, (, METIS -), Lua.

.6 ( ) “Bulldozer”, , “” “”.

En la Fig. se muestran diagramas de barras de los anchos de los niveles de IPF reales de copias de pantalla cuando el sistema SPF @ home está en funcionamiento (la media aritmética de los anchos se muestra con una línea de puntos, a) y el esquema simbólico del método "Bulldozer" - b) — . SPF@home (- , a) “Bulldozer” - )

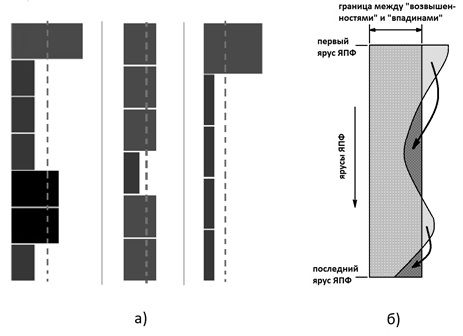
, ( 1,5-2 ) , (- ).

.. ( Lua) (., c , , .).

SPF@home ( ) . , . ( ) ( , , ). , .

, ( ) .

1. .., .. . — .: -, 2002. — 608 c.
2. ., . . : — , , 2012. — 420 c.
3. AlgoWiki. . URL: http://algowiki-project.org ( 31.07.2020).
4. .. . . — .: -, 2018. — 390 .
5. Roberto Ierusalimschy. Programming in Lua. Third Edition. PUC-Rio, Brasil, Rio de Janeiro, 2013. — 348 p.

¿Existe paralelismo en un algoritmo arbitrario y cómo usarlo de la mejor manera?

More articles: